一種基于態勢關聯的地圖匹配算法＊

滕志軍 何義昌 李昊天 滕利鑫

（東北電力大學，吉林 132012）

主題詞：地圖匹配 態勢關聯 態勢預測 仿真 航向角差分

1 前言

地圖匹配是將車輛行駛軌跡與地理信息系統中的路網相關聯的定位修正方法[1]。傳統的地圖匹配算法包括投影法[2]、概率統計法[3]、曲率積分值方法[4-5]等。投影法計算出定位點與各候選路段的距離度量值，在所有候選路段中，選擇距離度量值最小的作為匹配路段[6-7]。概率統計法需要在導航傳感器提供的定位點周圍定義橢圓形或方形置信區域，如果置信區域內包含多個路段，則采用航向、連通性、速度和距離等標準評估候選路段。基于曲率積分值的地圖匹配方法通過計算GPS軌跡相鄰軌跡點之間的曲率和候選路段對之間的路徑曲率的相似程度進行地圖匹配。此外，國內外學者還采用其他算法開展地圖匹配，但是這些算法都缺少對車輛軌跡的預測。

本文提出一種基于態勢關聯的地圖匹配算法，首先利用傳統的地圖匹配算法得到匹配的候選路段，適當縮小匹配搜索范圍，然后利用本文提出的匹配算法實現路段匹配，并根據態勢關聯元素進行參數更新，從而提高位姿估計精度，可增強地圖匹配的穩定性，提高車輛行駛過程中的路段匹配精度。

2 基于態勢關聯的地圖匹配算法

在地圖匹配中，從時刻t0開始態勢關聯[8-10]，時刻t0前的定位點為歷史定位點，時刻t0后關聯得到的為態勢預測定位點。根據得到的各定位點的航向角和距離等態勢元素所組成的集合，利用電子地圖數據模板進行關聯評估[11]。態勢預測時對目標過去的運動狀態（包括目標的位置、速度、加速度等）進行平滑關聯，對目標的歷史運動軌跡進行評估以及對目標的未來運動軌跡進行態勢預測[12-13]。在地圖匹配中，態勢關聯主要解決t0時刻后如何更新態勢以及對當前態勢如何進行推算的問題，同時也為態勢評估提供前提條件。圖1所示為基于地圖匹配的態勢關聯示意。

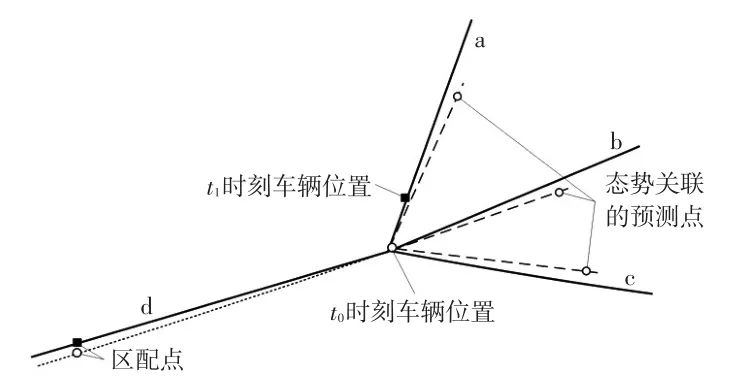
圖1 基于地圖匹配的態勢關聯示意

車輛行駛到t0時刻，下一個時刻（t1）車輛行駛的路段可能為a、b或者c。如果車輛繼續沿與d路段態勢相類似的b路段方向行駛，由于慣性導航的影響，車輛的位姿信息不會有太大變化；如果車輛下一時刻行駛在a或c路段，所提供的定位信息的連續性就會較差。在較長的一段時間內，導航定位系統定位精度難于保障，為提高其精度、連續性和魯棒性，在短時間內識別出交叉路口和多條交叉路口車輛改變方向后的軌跡，利用態勢關聯預測出的定位點參數和t1時刻定位點參數相關系數的匹配，可以在短時間內將車輛匹配到正確的道路上。

3 態勢關聯步驟

主要匹配步驟分為3步：首先對確定數據點進行量化，然后對預測點估計數據進行量化，最后通過計算各條候選路段歷史定位點和預測定位點的置信度來確定匹配路段的態勢評估。

3.1 定位點航向角元素提取

定位點航向角元素的提取步驟為：

a.將t0時刻位置點標定為坐標原點。

b.選出t0時刻前保存在關系型數據庫MySQL中的6個歷史數據點，并且將其轉化到所設定的坐標系下，分別為(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)、(x5,y5)、(x6,y6)。

從原點起，每兩個相鄰的點可以求得斜率：

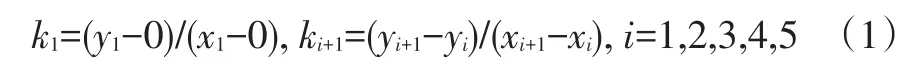
計算出所對應的航向角為θi=arctanki。

c.將電子地圖中相鄰的幾條候選路段各自的定位經緯度坐標轉化到步驟a所設定的坐標系中每條候選路段所對應的 7 個點(x7,y7)、(x8,y8)、(x9,y9)、(x10,y10)、(x11,y11)、(x12,y12)、(x13,y13)。

從(x7,y7)起，每兩個相鄰的點可以求得斜率：

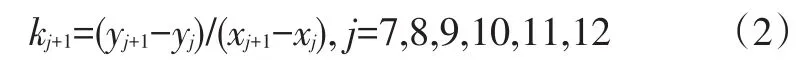
d.利用態勢評估模板進行態勢關聯，即求出車輛t0時刻以后的態勢關聯的4個時刻在該向量坐標下的坐標數據。以t0時刻為起點，態勢關聯出的下一時刻的斜率為：

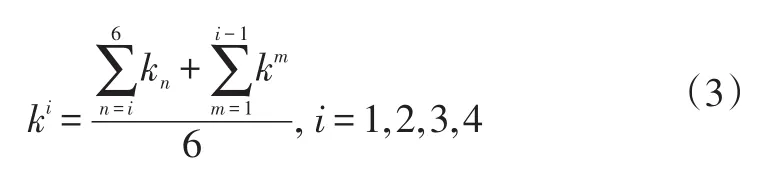
第i個時刻可能的坐標：

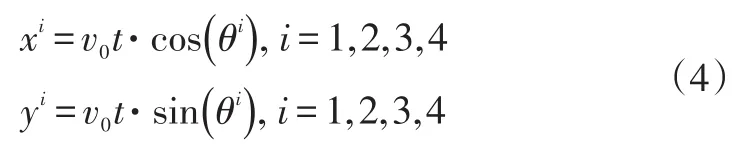
式中，θi=arctanki,i=1,2,3,4。

e.分別計算通過態勢關聯得到的4個坐標點(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)，從原點開始每兩個相鄰的點可以求得斜率：

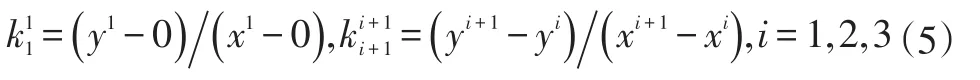
f.將相鄰的電子地圖中幾條候選路段各自的定位經緯度坐標轉化到步驟a所設定的坐標下。每條對應候選路段所對應的 4 個點(x5,y5)、(x6,y6)、(x7,y7)、(x8,y8)，從(x7,y7)開始每兩個相鄰的點可以求得斜率：

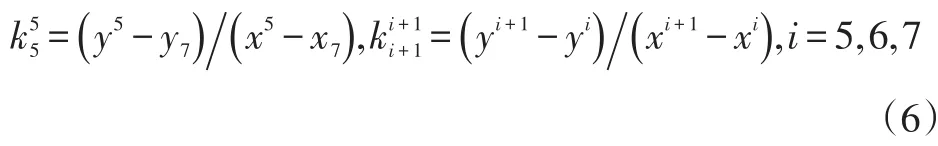
3.2 歷史軌跡相關系數

兩變量間的相關可以用許多統計值來測量，最常用的是皮爾森相關系數。皮爾森相關系數（Pearson Correlation Coefficient）也稱 皮爾森 積矩相關系數（Pearson Product-Moment Correlation Coefficient），是一種線性相關系數，是用來反映兩個變量線性相關程度的統計量[14]。歷史軌跡相關系數R表示為：

3.3 基于態勢關聯的航向角參數校準

在導航系統中，電子羅盤可測量航向角，陀螺儀主要測得動態變量（角速度）[15]，車輛行駛的速度矢量稱為航速，規定航速與正北方向的偏離角為航向角。為了提高匹配精確度，本文提出基于態勢關聯的航向角關聯預測對航向角進行校準。定義基于態勢關聯的航向角修正系數為Ug，車輛在Δt時間內的歷史航向角Δθ和在態勢元素提取等時間Δt內預測得到角度Δθy為：

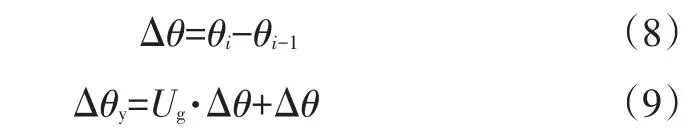
式中，Ug·Δθ為車輛在Δt時間內態勢關聯對歷史航向角的修正角度。

航向角修正系數Ug和態勢關聯軌跡相關系數R*分別為：

式中，Δθmap、Δθtra和Δθg分別為上一時刻電子地圖航向角、軌跡航向角和上一時刻航向角修正系數；為對應的電子地圖相鄰兩點斜率。

根據相鄰兩個時刻的航向角差分評估該時間段車輛需要匹配的候選路段，通過關聯修正系數對航向角進行補償[16]，進一步提高匹配的精度。

3.4 基于態勢關聯規則的匹配流程

依據態勢關聯規則，設定相對應的匹配流程如圖2所示。

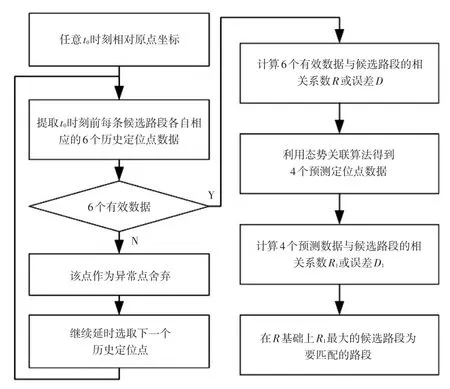
圖2 基于態勢關聯規則的匹配流程圖

4 結果與仿真分析

利用Novatel公司的高精度Span/DGPS組合導航系統在東北電力大學校園采集地圖信息數據，然后通過與Google衛星圖片的匹配對偏離道路的點進行離線修正，生成準確的參考軌跡。圖3和圖4分別給出了典型匹配點的軌跡圖和測試軌跡匹配圖。

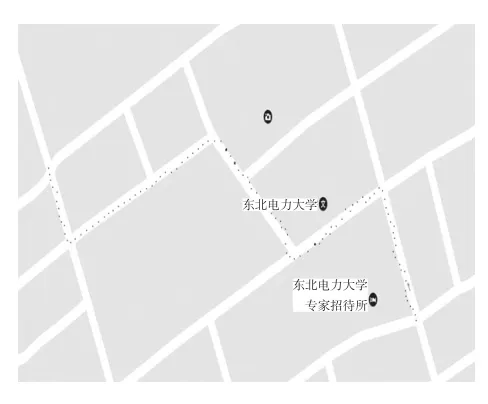
圖3 典型匹配點軌跡

圖4 測試軌跡匹配

圖5所示為基于經緯度數據態勢關聯的典型路段匹配效果。圖5中，最后路段的誤差是長時間的誤差累積造成的，此時車輛通過交叉路口進行轉彎，車輛容易將定位點置于兩條路的中間，導致定位點信息不準確。引用態勢關聯算法后，車輛在最后交叉路口轉彎后，車輛快速將定位信息匹配到了正確路段上，更新后的側向和縱向最大誤差分別為0.7m和3.7m。

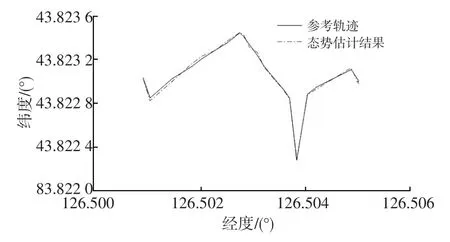
圖5 態勢關聯后的典型路段匹配效果圖

圖6所示為匹配路段上等時間間隔的航向角差分仿真結果。由圖6可知，采用態勢關聯算法得到的匹配效果優勢明顯，尤其在長時間誤差累積階段，圖像趨勢凸顯尖銳，說明數據更新更快，候選路段匹配度更高。

圖7所示為態勢關聯預測點匹配相關系數仿真結果。由圖7可知，態勢關聯的相關系數大于投影算法相關系數，說明態勢關聯后的相關性較好。匹配路段負相關系數數據減少，說明匹配的誤差減小，匹配精度得到提高。

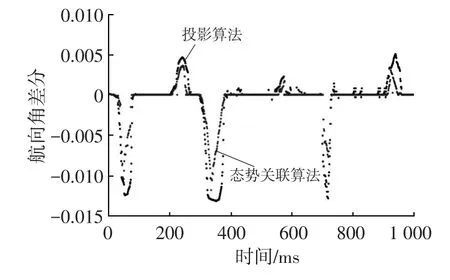
圖6 等時間間隔航向角差分

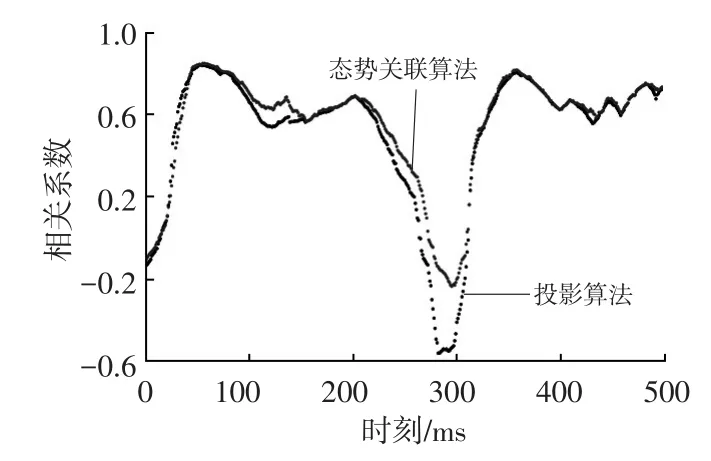
圖7 各時刻定位點相關系數

5 結束語

本文提出了基于電子地圖數據和態勢關聯軌跡特征的地圖匹配方法，并以此方法對部分交叉路口進行了匹配。結果表明，該算法匹配精度高，具有較高的魯棒性。該方法適合交叉路段和平行路段，尤其對交叉路段和分叉路口修正效果更為明顯。