異常情況下電動汽車鋰電池SOC估計

杜堅 謝聰

（西南石油大學，成都 610500）

主題詞：鋰電池 SOC估計 強跟蹤卡爾曼濾波

1 前言

對于電動汽車，電池荷電狀態SOC反映了汽車當前狀態下的續航能力，研究電池荷電狀態估計問題，對合理管理電池、確定汽車續航能力具有重要意義。

電池SOC無法直接測量，只能通過測量電池電壓、內阻等參數間接估計。電池SOC估計方法分為傳統算法和智能算法，傳統算法根據開路電壓與某一參數的對應關系進行測量，包括開路電壓法、內阻法、安時積分法等[1-3]。其中，開路電壓法在電池長期靜置后才可使用，無法應用于汽車行駛狀態；內阻法問題在于內阻難以測量；安時積分法由于使用積分算法而容易產生積累誤差。由上述分析可知，傳統SOC估計方法限制較多，因此當前SOC估計研究熱點集中在基于智能算法的SOC估計方面。智能算法使用算法的群智能性搜索SOC最優估計值，包括神經網絡算法、粒子群算法、卡爾曼濾波等[4-6]。

本文針對狀態突變、模型不準確、SOC初值誤差大等異常情況下SOC估計問題進行研究，提出了基于強跟蹤卡爾曼濾波算法的估計方法。仿真結果表明，該方法在以上特殊情況下能夠給出高精度的SOC估計值。

2 鋰電池模型及參數辨識

2.1 鋰電池模型

電池建模要遵循兩個原則：一是模型不能太復雜，保證計算量在接受范圍內；二是模型能準確模擬電池動靜態特性。選用電路模型模擬電池內部狀態，常用電路模型包括理想模型、戴維南模型、PNGV模型和雙階RC模型等[7,8]。雙階RC模型將電化學極化過程和濃度極化過程分開表示，與其它電池模型相比具有較高擬合精度，因此選用雙階RC模型，其結構如圖1所示。圖中Uoc為電池開路電壓；R0為電池歐姆內阻，反映電池濃差極化過程，即狀態突變后快速反應過程；RdCd回路反映電池電化學極化過程，即狀態突變后慢速反應過程；I為電池內部電流；Ut為電池端電壓。

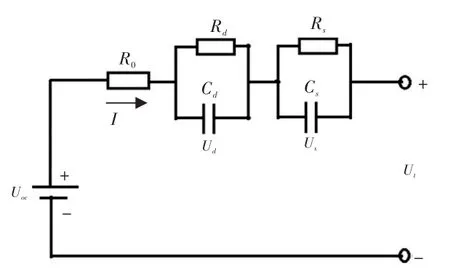
圖1 雙階RC模型[8]

鋰電池狀態空間方程是SOC估計的基礎，首先設定鋰電池狀態向量為：

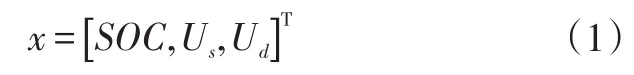
式中，Us為RsCs回路端電壓；Ud為RdCd回路端電壓；τs、τd為2個RC回路的時間常數。

則鋰電池狀態空間方程為：

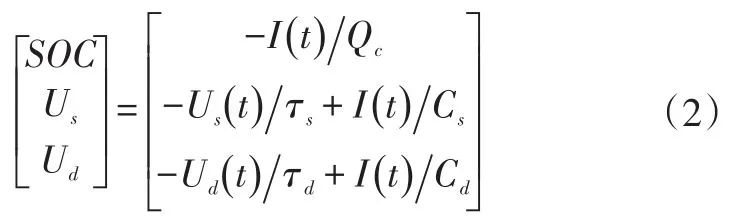
式中，I(t)為電池內部電流；Qc為電池容量；Cs為RsCs回路電容；Cd為RdCd回路電容。

輸出方程為：

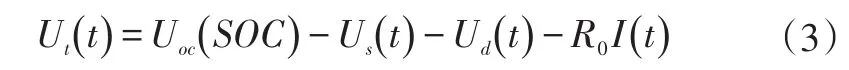
2.2 模型參數辨識

由圖1中雙RC模型可知，待辨識參數包括R0、Rs、Rd、Cs、Cd等，當電池SOC值不同時，參數值也不同，因此每隔10%SOC值進行1次參數辨識。由于鋰電池具有滯回特性，參數在充電和放電時數值相差較大，因此對充電和放電過程分別進行參數辨識。采用HPPC方法進行參數辨識，為了保證電池狀態穩定性，每次試驗后將電池靜置30min后再進行下次試驗。充電和放電過程參數辨識結果如表1和表2所示。

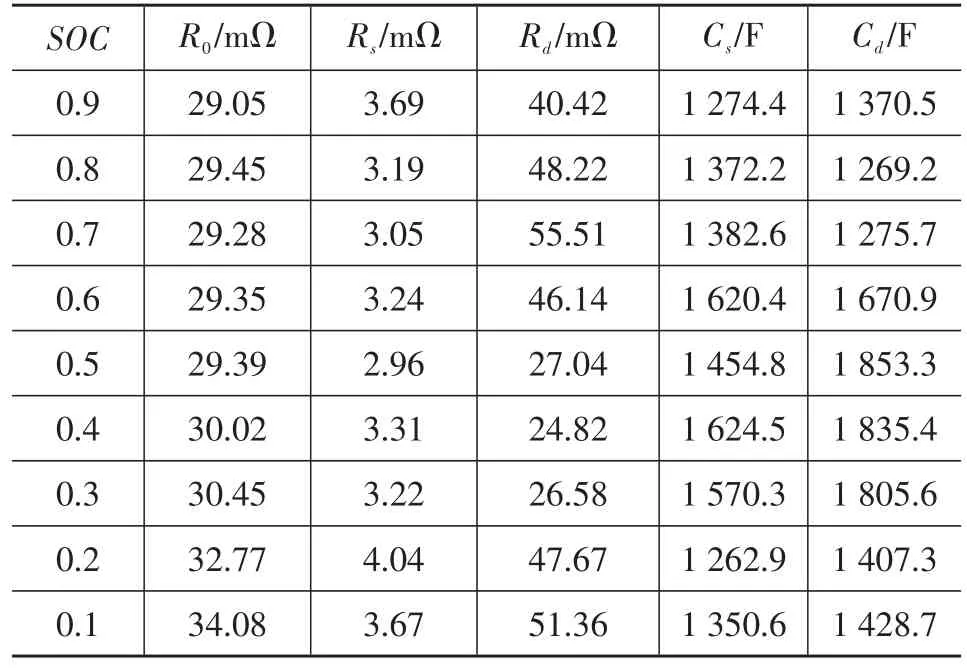
表1 放電過程參數辨識結果

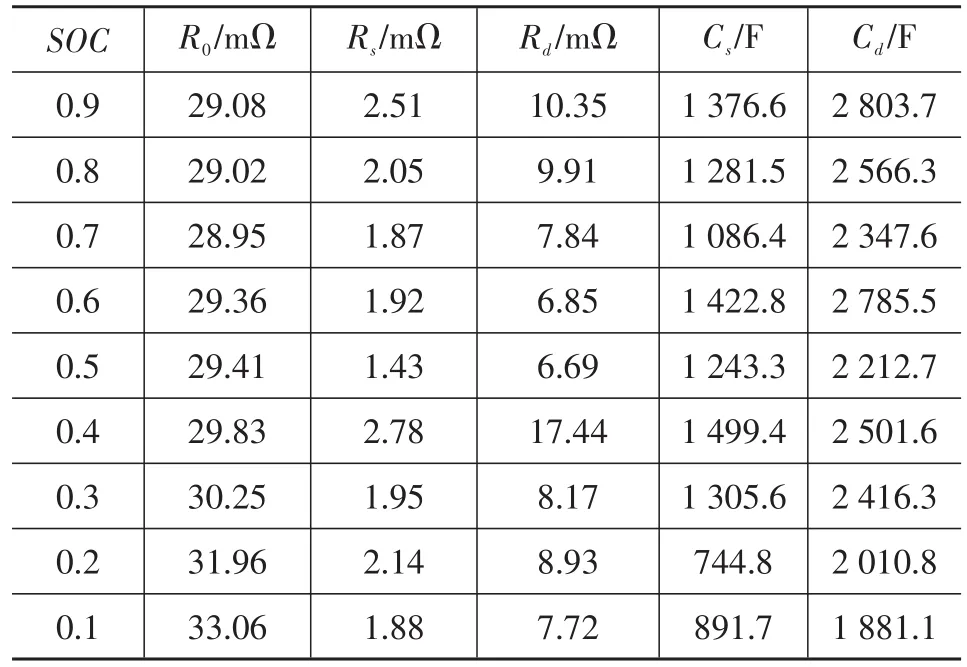
表2 充電過程參數辨識結果

2.3 開路電壓-荷電狀態關系

因式（3）中Uoc(SOC)的函數關系未知，所以需要建立Uoc與SOC之間的函數關系。經驗證鋰電池在充電和放電過程中，Uoc與SOC之間的函數曲線幾乎重合，滯回特性表現不明顯，因此取充電和放電過程的均值曲線建立函數關系式。利用25℃恒溫試驗方法進行函數關系辨識，將鋰電池在滿電狀態下靜置2 h使狀態穩定；然后放電5min，釋放電量為1 C；再靜置5min使狀態穩定，記錄靜置期間最大開路電壓并作為此SOC值時的開路電壓。重復以上步驟直至放電完畢，得到不同SOC值時的試驗數據，使用多項式擬合Uoc與SOC之間的關系式。

經驗證，7階多項式模型擬合精度比6階模型擬合精度高一個數量級，8階多項式模型擬合精度與7階模型相差不大，因此選用7階多項式進行擬合，結果如圖2所示，Uoc與SOC關系式為：

3 強跟蹤卡爾曼濾波算法

3.1 擴展卡爾曼濾波

卡爾曼濾波只適用于線性系統，對于鋰電池這種非線性系統，可使用擴展卡爾曼濾波進行狀態估計[9]。擴展卡爾曼濾波使用泰勒級數將非線性系統近似為線性系統，再使用卡爾曼濾波估計方法[10]。

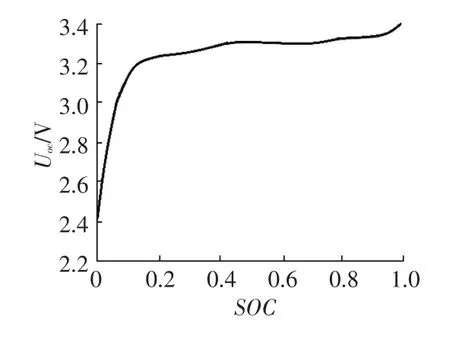
圖2 Uoc與SOC的擬合曲線

非線性系統狀態方程和觀測方程為：

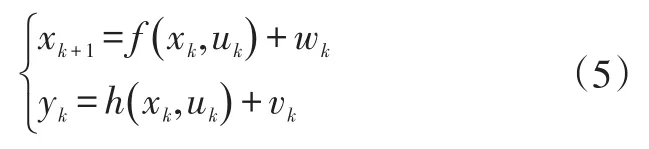
式中，f(xk,uk)為狀態轉移函數；wk為狀態噪聲；h(xk,uk)為觀測函數；vk為觀測噪聲。

使用泰勒級數將非線性函數f(xk,uk)、h(xk,uk)在處展開，保留零次項和一次項，得

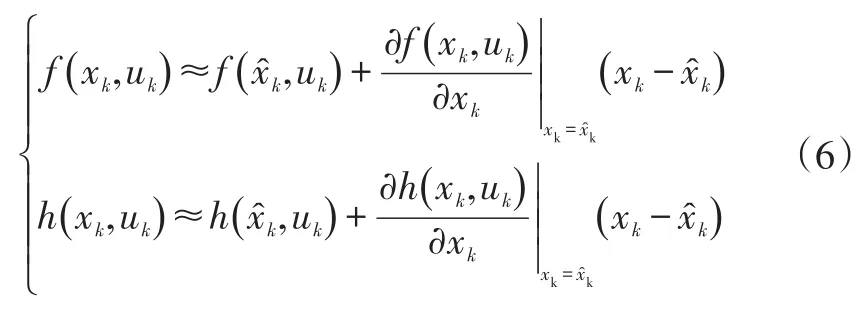
設

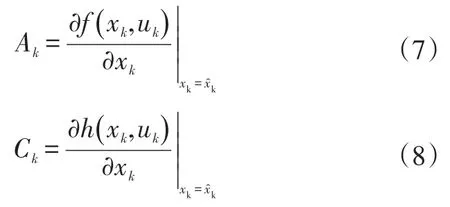
則可將式（5）近似為線性系統：

對此線性系統進行卡爾曼濾波估計使用的迭代公式為：

一步狀態估計方程：

估計誤差協方差矩陣：

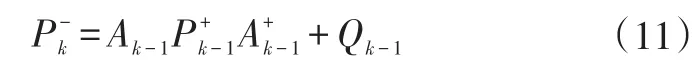
修正系數矩陣：

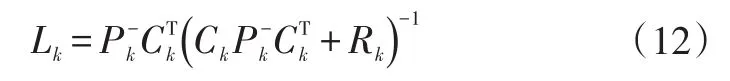
系統狀態更新公式：

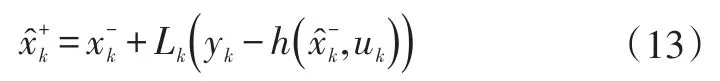
誤差協方差陣更新公式：

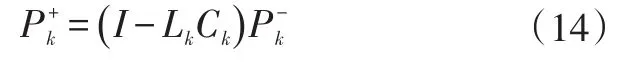
對此過程反復迭代就可以對鋰電池狀態進行實時最優估計，得到鋰電池SOC最優估計值。

3.2 強跟蹤卡爾曼濾波算法原理

對于電動汽車鋰電池SOC估計問題，存在以下異常情況：

a.汽車行駛過程中，由于爬坡、加速、制動等使電池電流、開路電壓等狀態發生突變；

b.電池模型無法完全模擬電池復雜的內部過程，且電池使用過程中模型參數容易變化，使電池模型與實際狀態相差更大；

c.電池SOC初始值難以準確給出，存在較大初值誤差等。

對于以上異常情況，需要一種在任何情況下都能夠強行使估計殘差保持正交，即在任何情況下都能夠將殘差強行轉化為白噪聲的濾波方法。基于此，引入時變漸消因子，提出了強跟蹤卡爾曼濾波算法。

通過引入估計殘差，將擴展卡爾曼濾波算法中系統狀態更新公式改寫為：

強跟蹤卡爾曼濾波的實質是通過設計增益矩陣Lk，使殘差γk為高斯序列，即滿足：

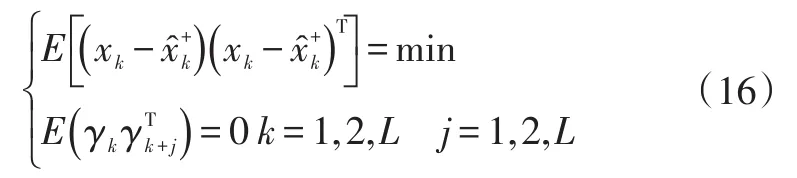
式（16）表示當電池出現狀態突變、模型不準確、SOC初始誤差大等異常情況時，狀態估計值與實際值會產生較大的殘差，通過在線確定增益矩陣Lk，強行使殘差相互正交保持高斯特性，保持對系統的精確跟蹤；若沒有異常情況，上式自然成立，此時強跟蹤卡爾曼濾波退化為擴展卡爾曼濾波。

3.3 強跟蹤卡爾曼濾波算法實現

分析擴展卡爾曼濾波算法中修正系數矩陣表達式可知，可以通過調節改變修正系數矩陣。為了實現算法的強跟蹤特性，引入漸消因子λk減小舊數據在估計值中的權重，即誤差協方差矩陣改進為：

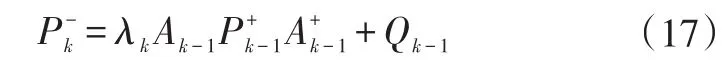
可以通過式（16）中的正交公式對式（17）求解，求解方法為梯度法和非線性規劃法，但是求解過程復雜、計算量巨大，因此給出次優漸消因子為：

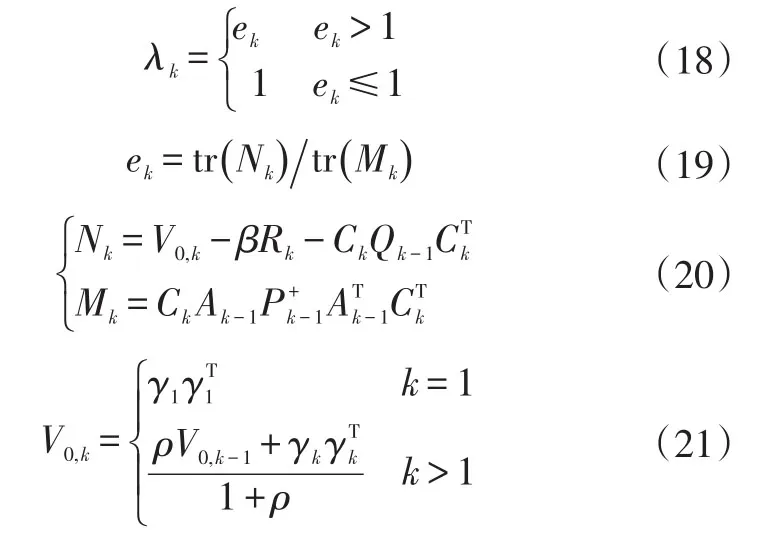
式中，λk為次優漸消因子；tr（）為矩陣的秩；V0,k為殘差協方差陣；ρ為遺忘因子；β為弱化因子，且β≥1。

將式（17）和式（18）代入到修正系數矩陣公式，得到強跟蹤卡爾曼濾波修正系數矩陣。

將鋰電池的狀態空間方程和觀測方程進行離散化處理，即

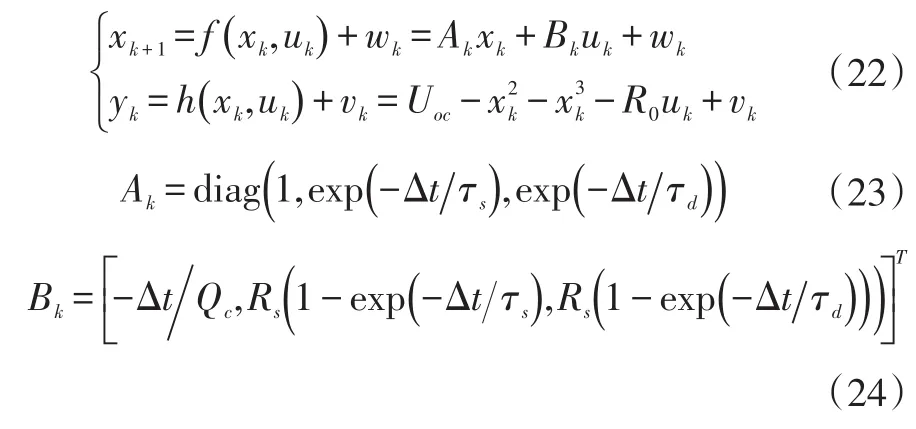
根據式（22）給出的離散方程、式（18）給出的次優漸消因子計算方法，強跟蹤卡爾曼濾波算法使用的迭代公式為：

狀態一步估計：

計算觀測輸出：

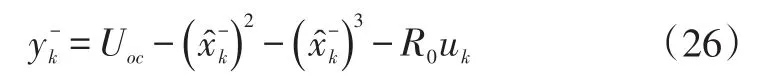
誤差協方差矩陣：

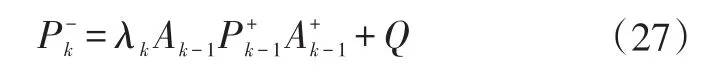
修正系數矩陣：

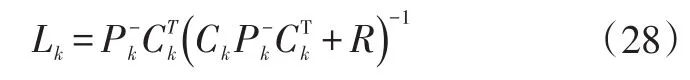
系統狀態更新公式：

誤差協方差矩陣更新公式：

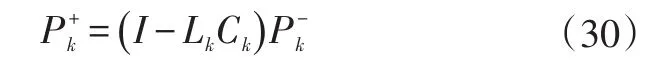
此6個公式反復迭代就實現了鋰電池SOC的強跟蹤最優估計。

4 仿真驗證

設計了兩組仿真驗證，第1組仿真驗證用于驗證強跟蹤卡爾曼濾波對模型不準確、系統狀態突變這兩種異常情況下的估計精度；第2組仿真驗證用于驗證電池SOC初始誤差較大情況下的SOC估計精度。

4.1 第1組仿真驗證

為驗證算法對系統模型不準確和狀態突變時的估計精度，在開路電壓中加入均值為0.01、方差為0.1的隨機噪聲，用于模擬模型不準確的情況；同時設計了帶有電流突變的充放電試驗，用于模擬狀態突變。數據采集頻率為1 Hz，采集時間共8 320 s，仿真得到的電流、電壓曲線如圖3所示。

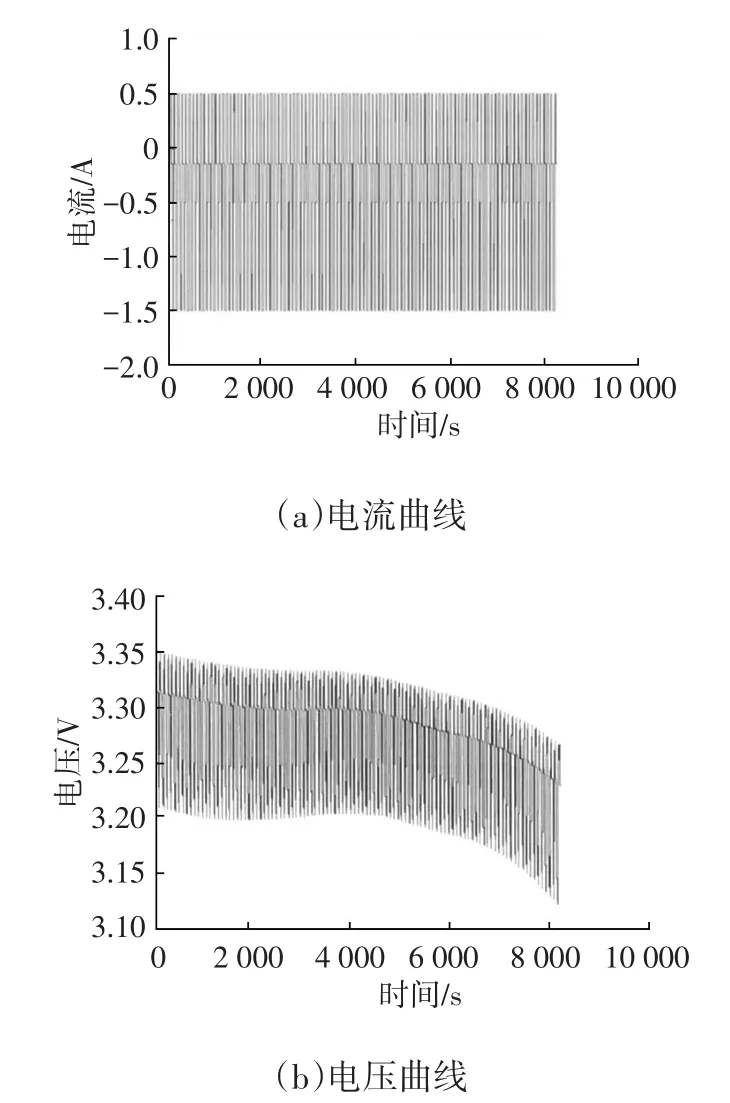
圖3 數據采集結果

分別使用擴展卡爾曼濾波和強跟蹤卡爾曼濾波算法對電池SOC值進行估計，算法參數設定為：遺忘因子ρ=0.95、弱化因子β=1.2、觀測噪聲R=0.05、狀態初始值x0=[8 0 %,0,0]T、誤差協方差矩陣初始值P0=I3×3、狀態噪聲Q=diag(0 .001,0.1,0.1)。兩種算法對電池SOC估計結果如圖4所示。

從圖4可看出，在系統模型不準確和狀態突變的情況下，擴展卡爾曼濾波得到的SOC估計結果波動較大，而強跟蹤卡爾曼濾波得到的SOC估計值波動較小。為更加直觀比較兩個算法的估計結果，對估計誤差進行統計，強跟蹤卡爾曼濾波的估計誤差維持在2%之內，而擴展卡爾曼濾波的最大估計誤差達到了4.5%。這是因為當出現模型不準確和狀態突變等異常情況時，強跟蹤卡爾曼濾波能夠及時調整修正系數矩陣，使殘差成為白噪聲序列，確保估計值的最優；而擴展卡爾曼濾波的非線性誤差、狀態突變誤差、模型不準確誤差相互疊加，使估計誤差較大。

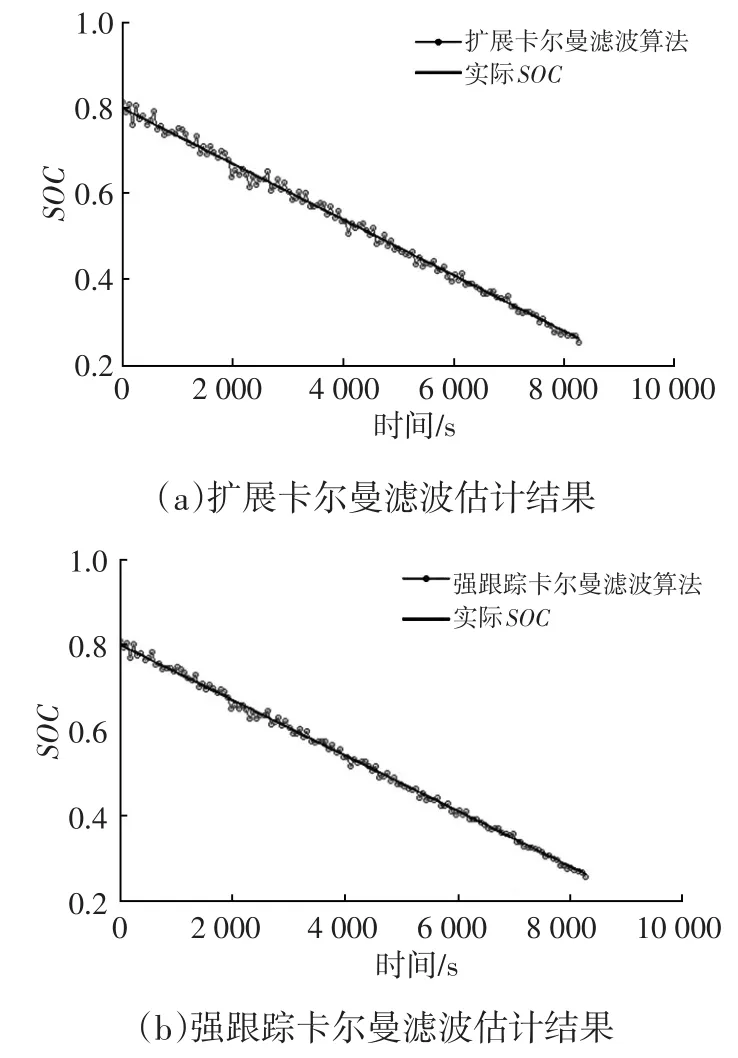
圖4 兩種算法的SOC估計結果

4.2 第2組仿真驗證

第2組仿真驗證的目的是驗證電池SOC初始誤差較大時估計精度問題。根據式（4）可以準確計算出SOC初始值，但是測量開路電壓時，要求電池靜置0.5 h以上，這一條件在汽車使用過程中難以滿足，所以多數情況下電池SOC初始值難以計算。仿真時設置電池SOC真值為80.5%，為了驗證算法對初始誤差的估計精度，將SOC初始值設置為40%，分別使用擴展卡爾曼濾波和強跟蹤卡爾曼濾波對電池SOC進行估計，算法參數與第1組仿真一致。為了更加清晰地比較兩算法對初始誤差的修正速度，給出了前50個數據的估計結果，如圖5所示。

圖5 前50數據估計結果（放大圖）

從圖5可看出，兩種算法最終都可以收斂到真值，但是強跟蹤卡爾曼濾波算法在15 s內就收斂至真值附近，而擴展卡爾曼濾波在40 s時才收斂到真值附近，這充分說明強跟蹤卡爾曼濾波應對SOC初始誤差時具有更快的收斂速度。這是因為強跟蹤卡爾曼濾波的修正系數矩陣能夠依據異常情況自適應地調整，使SOC估計值快速向真值靠攏。

5 結束語

建立了鋰電池的雙RC等效電路模型，在分析擴展卡爾曼濾波基礎上，提出了強跟蹤卡爾曼濾波算法。通過仿真驗證表明，所提出的強跟蹤卡爾曼濾波算法對狀態突變、模型不準確、SOC初始誤差等異常情況時的估計精度和收斂速度明顯優于擴展卡爾曼濾波。因此通過調整增益矩陣，強行使殘差正交，可以使強跟蹤卡爾曼濾波算法應對異常情況時，SOC估計精度依然很高。