一種改進的電動汽車鋰電池RC滯后模型及其應用＊

孫川 褚端峰 李海波 王建宇

（1.黃岡師范學院，黃岡 438000；2.武漢理工大學，智能交通系統研究中心，武漢 430063；3.東風汽車公司技術中心，武漢 430056）

主題詞：電動汽車 荷電狀態 一階RC滯后模型 自適應粒子濾波

1 前言

動力電池的成本、能量密度、循環壽命等是制約電動汽車發展的關鍵因素。解決這一問題，可以從兩個角度出發：一是開發成本低、能量密度高、循環壽命長的電池；二是開發有效的電池管理系統，通過科學管理充分發揮其性能優勢[1]。荷電狀態（State Of Charge，SOC）估計是電池管理的重要內容，研究電動汽車SOC估計問題，對于電池科學管理、合理安排充電時機具有現實意義。

電池SOC估計方法可以分為3類：傳統方法，包括開路電壓法[2]、內阻法[3]、安時積分法[4]等；基于黑箱模型的估計方法，包括神經網絡模型[5]、模糊邏輯模型和支持向量回歸模型[6]等；基于狀態空間模型的估計方法，常用方法有卡爾曼濾波[7]、粒子濾波[8]、H∞算法等。其中，傳統方法不適宜在電池使用時進行估計，基于黑箱模型的估計方法對試驗數據的數量和準確性依賴較強，基于狀態空間模型的估計方法是當前研究的重點。粒子濾波的各種自適應改進及應用也被廣泛研究：Li[9]提出了粒子數隨時間自適應變化的粒子濾波方法，此方法以相對熵（Kullback-Leibler Divergence）為依據確定下一時刻粒子數，實現了計算量減小的目的；Zuo等[10]提出了重要密度函數自適應更新的粒子濾波方法，解決了采樣效率低的問題，提高了算法估計精度；Straka等[11]依據估計誤差調整粒子數量，將估計誤差控制在一定范圍內，同時致力于減少計算量。

以上粒子濾波的自適應改進方法是算法自身的改進，本文結合電池SOC估計問題，充分利用已辨識的模型信息，以模型估計值與觀測值之差為依據，自適應調整模型的狀態噪聲和觀測噪聲，達到了提高電池SOC估計精度、速度和魯棒性的目的。

2 鋰電池模型及參數辨識

2.1 鋰電池模型

本文使用等效電路模型對鋰電池進行建模。等效電路中有3個常見模塊：

a.歐姆內阻模塊。內阻R0由電極材料、隔膜電阻、電解液對電荷的運動阻力產生。

b.RC網絡模塊。電池使用時具有極化現象，本文使用極化電容Cp與極化電阻Rp組成的RC網絡模擬這一過程。對電池建模時，通常使用RC網絡串聯提高模型精確度。但4階及以上的RC網絡會大幅增加計算量，而模型精度提高很小，故一般使用3階及以下的RC網絡。第i個RC網絡端電壓與電阻、電容的關系為：

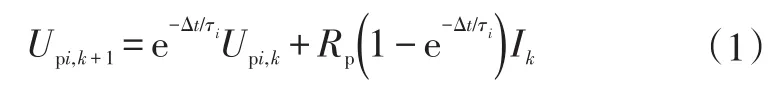
式中，Δt為采樣周期；τi=RiCi為時間常數；Upi,k為k時刻第i個RC網絡的端電壓；Rp為極化電阻；Ik為k時刻RC網絡電流。

c.滯后模塊。滯后模塊用于反映電池電壓變化相對于電流變化的延遲現象。美國的Plett教授給出了滯后模塊的公式[12]：

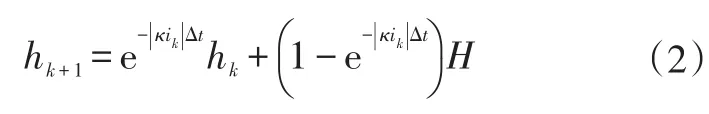
式中，hk為k時刻滯后電壓；κ為衰減因子；ik為k時刻電流；H為最大滯后電壓。

使用上述模塊，本文分別建立了1階、2階、3階RC及RC滯后模型共6個模型，圖1給出了1階RC及RC滯后模型，2階與2階以上模型在1階模型基礎上串聯相應數量的RC網絡。

1階RC模型方程為：

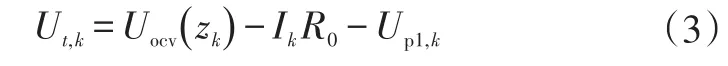
式中，Ut,k為k時刻電池輸出電壓值；zk為k時刻電池SOC值；Uocv為開路電壓。

為了保證擬合精度，本文使用n次多項式擬合Uocv～z關系式，即

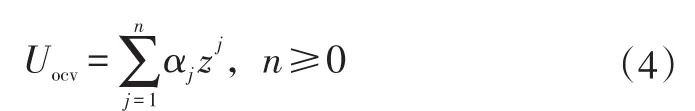
式中，αj為擬合系數。

1階RC滯后模型方程為：

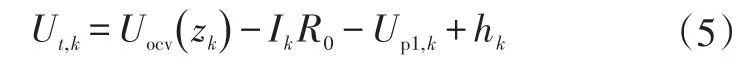
2階RC模型和RC滯后模型方程分別為：

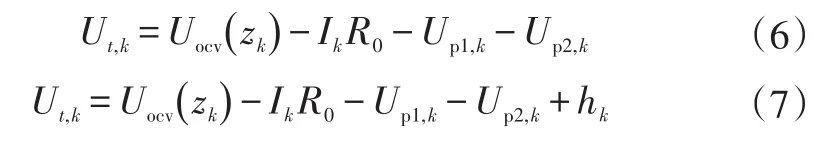
3階RC模型和RC滯后模型方程分別為：

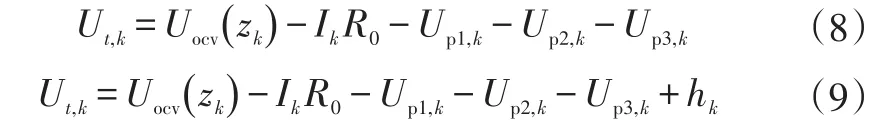
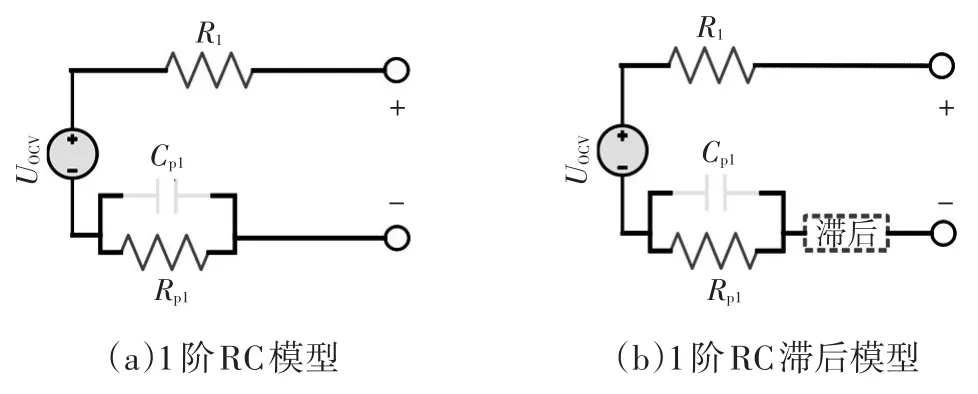
圖1 1階RC及RC滯后模型

2.2 模型參數辨識

首先使用試驗法和多項式擬合對式（4）進行辨識，試驗要求在25℃恒溫條件下進行，電池充滿電后靜置2 h使其狀態穩定，然后放電5min，釋放電量為1 C，再次靜置5min用于穩定狀態，記錄靜置期間的最大開路電壓作為此SOC下的開路電壓。重復以上步驟直至放電完畢，得到不同SOC值下的試驗數據，使用多項式擬合得Uocv～zk關系式為：

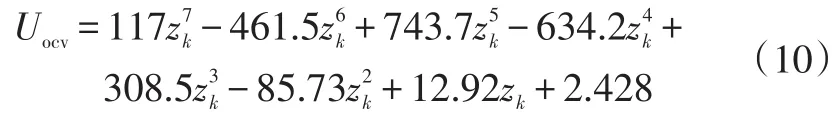
對于1階、2階、3階RC及RC滯后模型，首先進行混合動力脈沖能力特性（Hybrid Pulse Power Characteristic，HPPC）測試，而后使用粒子群算法[13]搜索最優解，以模型端電壓誤差的均方根為適應函數，綜合考慮模型誤差與計算量選擇鋰電池的等效模型。參數辨識以SOC每10%為一個區間，HPPC測試數據如圖2所示。

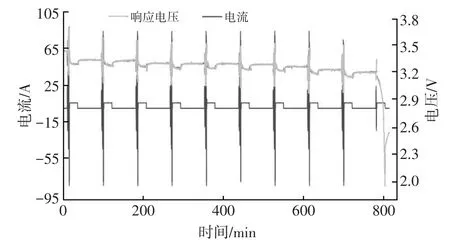
圖2 鋰電池HPPC測試數據

在粒子群算法中，粒子速度的更新受自身速度、自身歷史最優位置、種群最優位置的影響，向自身歷史最優位置和種群最優位置靠攏。使用粒子群優化算法搜索各模型的最優參數，結果如圖3所示。

圖3 各模型參數優化結果

通過計算端電壓誤差均方根的平均值，可以看出模型精度最高的是3階RC滯后模型，其次為1階RC滯后模型，兩者平均值相差約0.8mV，綜合考慮模型精度和計算量，本文選擇1階RC滯后模型作為鋰電池模型。

2.3 鋰電池空間模型

依據式（5）的1階RC滯后模型和式（4）給出的Uocv～z模型，選擇狀態向量x k=(Up1,k,hk,zk)T，將鋰電池等效電路模型和開路電壓方程離散化，得到狀態轉移方程和觀測方程分別為：

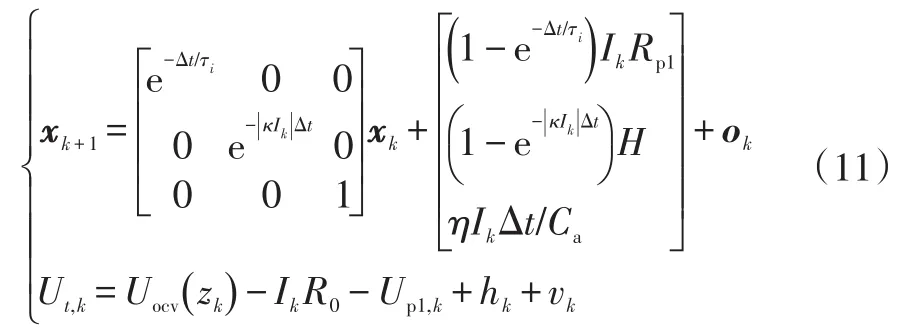
式中，Ca為電池可用容量；η≈1為庫倫系數；o k、vk分別為過程噪聲和觀測噪聲。

分析式（11）可知，R0、Up1,k、hk經過參數辨識過程已知，Ik、Ut,k可以實時測量，通過粒子濾波方法調整vk，使Uocv(zk)更加準確，即可根據式（10）計算出SOC。

3 自適應粒子濾波

3.1 傳統粒子濾波分析

由式（11）可以看出，鋰電池空間模型為非線性模型。傳統的卡爾曼濾波無法應用于非線性系統，擴展卡爾曼濾波又會帶來較大的非線性誤差，因此本文選用粒子濾波方法。粒子濾波實質是利用后驗概率分布對變量進行估計。

粒子濾波已經非常成熟，算法原理可參考文獻[14]、文獻[15]，在此簡要分析。記某一非線性空間方程為：

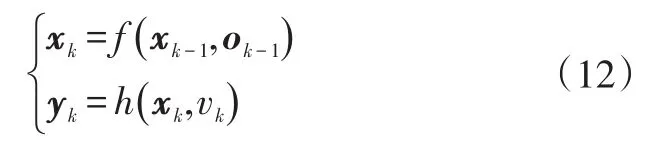
式中，x k、y k分別為k時刻的狀態向量和觀測量；f()、h()均為已知函數。

記系統狀態的后驗分布為p(x k|y k)，但其不具有標準形式，難以采樣。使用重要性采樣方法，引入容易采樣的概率分布q(x k|y k)，要求q(x k|y k)也定義在狀態空間中，取值范圍大于p(x k|y k)。q(x k|y k)被稱為重要性函數，在重要性函數下采集N個樣本，得到樣本集。

將重要性函數引入后驗分布中，得

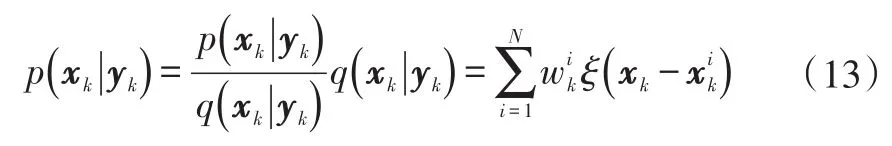
式中，ξ為狄拉克函數；為歸一化后k時刻第i個樣本的權值，且

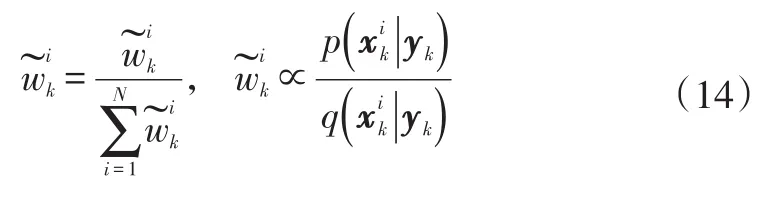
為了實現濾波過程的遞推計算，將重要性函數變形，并結合貝葉斯估計理論，可得

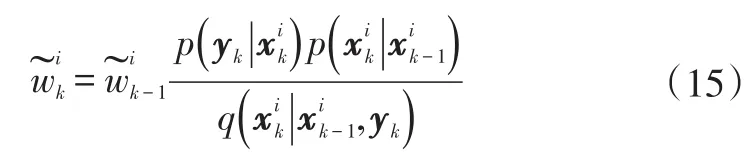
算法經過若干次迭代后，會出現粒子退化現象，也就是權重大的粒子會保持優勢，甚至越來越大，其他大量粒子權重越來越小，不僅產生了無用計算，而且估計精度也會降低。為解決這一問題，需要進行粒子重新采樣。

本文使用有效樣本數Neff評價粒子退化程度，作為粒子是否需要重新采樣的依據：

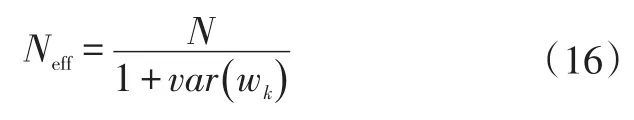
式中，var()為方差函數；N為實際粒子數。

對有效樣本數設置一個閾值Nth，若Neff≤Nth則說明粒子退化嚴重，需要重新采樣。

本文使用隨機重采樣方法進行重新采樣。首先對歸一化權值進行累加，得；其次在[0,1]上產生N個隨機數{uj}(j=1,…N)；搜索使cl≥uj成立的最小l，使新粒子，同時定義每個粒子權重為1/N，即可實現粒子重采樣。

3.2 自適應粒子濾波提出

現有的自適應粒子濾波方法是對狀態噪聲的自適應調整：

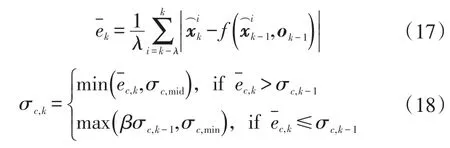
式中，λ為平滑濾波窗口；σc,k為自適應調整后的狀態噪聲；c為狀態向量的某一狀態變量；β∈[0.1,1]為衰減因子；σc,min為狀態c的最小噪聲方差；σc,mid為中等噪聲方差。

本文在此自適應粒子濾波基礎上進行改進，對觀測噪聲也進行自適應調整。改進思路為：建立等效模型時確定模型的誤差范圍，將狀態估計值代入觀測方程后得到觀測估計值，則觀測值的估計誤差也應在一定范圍內，如果觀測值誤差與模型誤差偏差較大，則需要較大的觀測噪聲方差使算法快速收斂。

3.2.1 確定觀測誤差邊界

觀測誤差可認為服從正態分布，記第i個粒子的實測值為，模型估計值為，實測值與估計值誤差為，誤差平均值記為μ，標準差記為δ，則

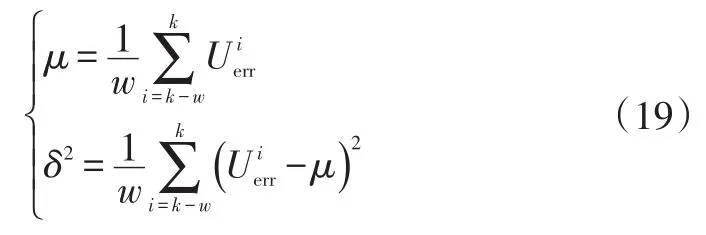
式中，w為辨識區間的數據個數。

根據大數定律，當w足夠大時，觀測誤差的均值和方程可以使用μ和σ2近似代替，根據參數的區間估計原理，取置信度為95%，得到觀測誤差邊界為，其中Ua為標準正態分布的上分位數。

3.2.2 觀測誤差自適應調整

將狀態估計值代入觀測方程，得到的觀測估計值誤差可能來源包括狀態噪聲、觀測噪聲、初值誤差等。一般來講，狀態噪聲和觀測噪聲在一定范圍內，而初值誤差等其他干擾可能引起較大誤差，參考上文中設定的觀測誤差邊界，本文觀測噪聲自適應調整為：

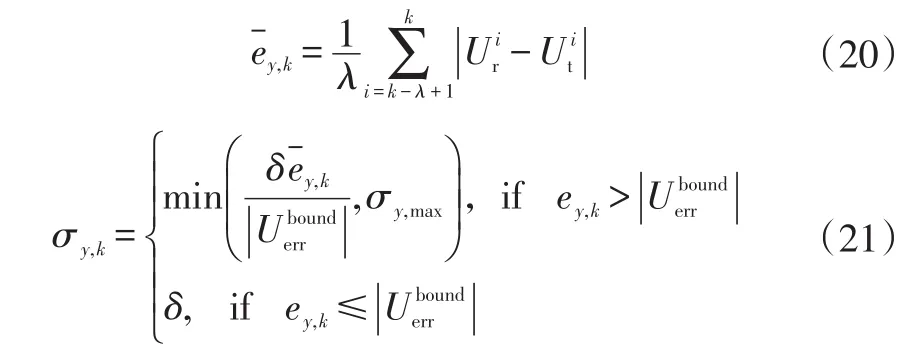
式中，ey,k為觀測誤差估計值；σy,k是自適應調整后的觀測誤差標準差；σy,max為觀測量的最大噪聲標準差差設定值。

式（20）和式（21）使用誤差平均值作為判斷標準，是為了防止抖動的干擾。

3.3 基于自適應粒子濾波的SOC估計

本文基于電池1階RC滯后模型的狀態空間方程和自適應粒子濾波方法，給出電池SOC估計流程如圖4所示。其中，初始化參數包括粒子、粒子權重、初始化噪聲方差、有效閾值、SOC、極化電壓、滯后電壓、粒子數等，粒子權值的計算公式為，k時刻狀態估計值為。

圖4 SOC估計算法流程

4 仿真驗證

4.1 收斂速度驗證

本次仿真中，SOC初始真值設置為0.80，SOC估計值設置為0.50，即初始誤差到達了0.30，分別使用傳統粒子濾波方法和本文提出的自適應粒子濾波方法進行SOC值估計，如圖5所示。

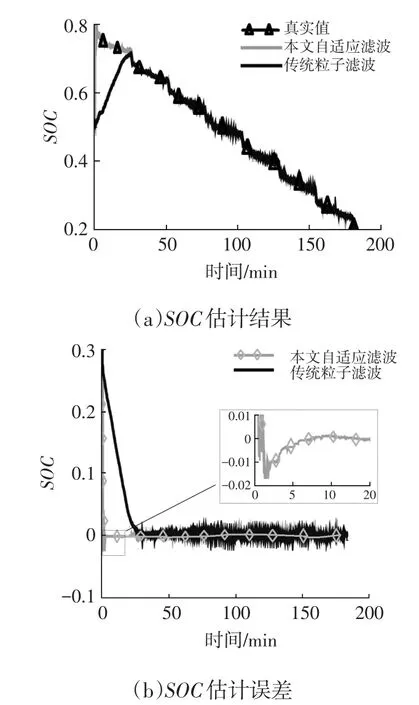
圖5 兩種算法的SOC估計結果

由圖5可以看出，在電池SOC初始誤差較大情況下，本文提出的自適應粒子濾波在第30 s左右收斂到了真實值附近，而傳統粒子濾波在24min后才收斂到真實值附近，說明本文提出的自適應粒子濾波在收斂速度和魯棒性方面具有明顯優勢。這是因為本文提出的自適應濾波在現有自適應算法基礎上，通過觀測誤差值與設定誤差邊界比較，實現了觀測噪聲依據觀測誤差的自適應調整。

4.2 收斂精度驗證

為了驗證本文提出算法的SOC估計精度，將SOC的估計區間設置為0.80～0.20，SOC初始值設置為0.70，即存在0.10的初始誤差。分別使用傳統粒子濾波與本文提出的自適應粒子濾波對SOC進行估計，得到的估計值和估計誤差如圖6所示。

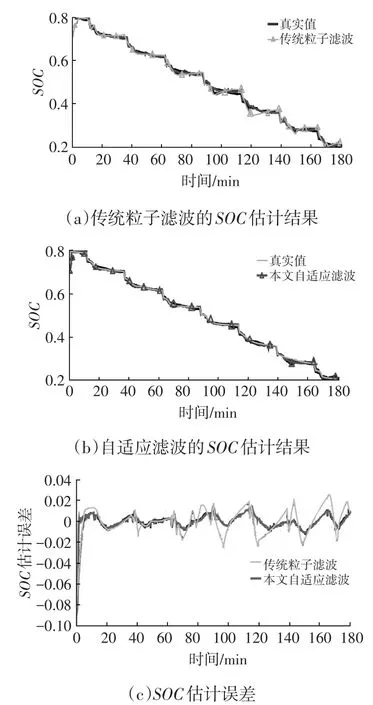
圖6 兩種算法對SOC估計結果

為了更加精確地對比兩種算法的估計精度，表1給出了兩種算法對SOC估計的統計數據。

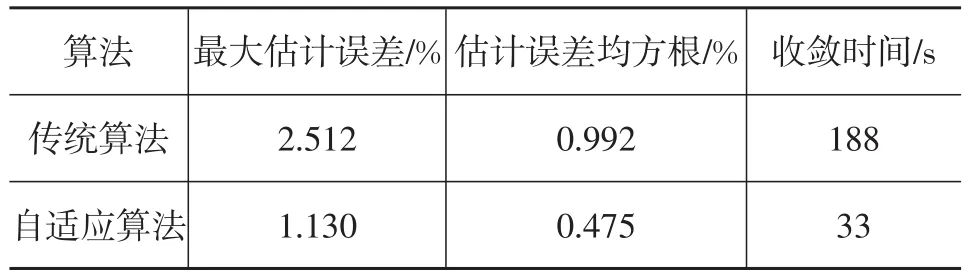
表1 兩種算法的SOC估計統計數據

由圖6和表1可以看出：兩種算法對SOC估計精度都較高，均未超過3%，但自適應粒子濾波估計算法精度更高；自適應濾波的估計誤差比傳統方法更加穩定；從收斂時間上看，自適應算法極大地提高了收斂速度。自適應算法在收斂精度、收斂速度上的優勢，源于自適應算法對狀態噪聲和觀測噪聲的自適應調整，使狀態噪聲和觀測噪聲能夠適應環境和其他因素引起的誤差變化。

5 結束語

本文建立了電池的1階RC滯后模型，提出了自適應粒子濾波算法，仿真結果表明：在初始誤差較大時，本文提出的自適應濾波算法具有很快的收斂速度和很好的魯棒性；與傳統粒子濾波相比，本文提出的自適應算法收斂精度高、收斂穩定性好、收斂速度快。這說明通過觀測誤差自適應調整觀測噪聲，使其對各種因素引起的誤差具有自適應性，可以提高算法的估計速度和精度。