基于CEEMDAN和1.5維譜的滾動軸承早期故障診斷方法

黃慧杰　孫百祎　任學平　劉淮全

摘要：針對滾動軸承早期故障難以識別的問題，提出一種自適應白噪聲的完備總體經驗模態分解（complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN）和1.5維譜相結合的滾動軸承故障診斷方法。該方法首先運用CEEMDAN對振動信號進行分解，得到一系列IMF分量，然后根據峭度準則以及相關系數準則提取一個包含主要故障信息的IMF分量，最后對提取的IMF分量進行1.5維譜分析，通過分析譜圖中突出成分以確定軸承故障類型。利用仿真信號和工程實驗數據對該方法進行分析驗證，所得出結果的譜圖均比用單一方法得出的譜圖清，充分證明該方法在滾動軸承早期故障診斷中的優勢。

關鍵詞：滾動軸承;早期故障;自適應白噪聲的完備總體經驗模態分解;1.5維譜

中圖分類號：TH133.33

文獻標志碼：A

文章編號：1674–5124（2019）02–0151–06

0 引言

軸承在機械設備運行中發揮無可替代的作用，發生損傷后，會影響機械設備中其他元件的正常工作，損傷的擴大會導致一系列故障，造成嚴重經濟損失，所以能夠對軸承早期故障進行及時地檢測和診斷具有重要意義。但軸承出現早期故障時，其故障特征十分微弱，周圍環境的干擾會使振動信號復雜化，導致故障特征難以提取[1-3]。

經驗模態分解[4]（EMD）作為處理復雜信號的工具，得到廣泛應用，但是EMD存在模態混疊現象。為了解決這一問題，EEMD[5-6]被提出來，通過向信號中增加高斯白噪聲，顯著減少模態混疊，但是該方法運算量大，對添加高斯白噪聲的標準差以及次數依賴比較大。Torres等[7]提出了一種自適應白噪聲的完備總體經驗模態分解（CEEMDAN），它能夠自適應地選擇加噪參數，不僅改善了分解的效果，而且提高了分解的速率。

CEEMDAN作為復雜信號的前處理工具，需要與合適的后處理方法結合才能更好提取故障特征[8]。1.5維譜[9-11]具有基頻分量加強特性、耦合諧波分量檢測性質以及抑制白噪聲等優良特性，這些特性說明1.5維譜在信號的特征提取方面具有一定優勢，十分適合作為CEEMDAN的后處理方法。

結合自適應白噪聲的完備總體經驗模態分解在抗模態混疊方面的優點，以及1.5維譜在特征提取方面的優勢，本文提出了將CEEMDAN和1.5維譜相結合的滾動軸承早期故障診斷的方法，并通過仿真信號以及工程實驗數據分析驗證方法的有效性。

1 基礎理論介紹

1.1 CEEMDAN

EMD將復雜信號分解為多個IMF與殘量之和。EEMD是在EMD基礎上在每次分解前加入預先設定好的高斯白噪聲。CEEMDAN是在每次分解前加入自適應的高斯白噪聲來計算唯一殘余信號，在該算法中，y（t）為原始信號，用IMFk表示其分解得到的第k個模態分量，定義Ek（·）為通過EMD分解得到的第k個模態分量，ni（t）為加入滿足正態分布的高斯白噪聲，對y（t）進行N次試驗，分解過程N一般取102數量級。其具體步驟如下：

利用EEMD算法分解得到第1個模態分量：

2）計算第1個殘余分量：

3）進行i次試驗每次對R1（t）+εE1[ni（t）]進行分解，常量ε取10?2數量級，直至得到第1個模態分量，定義第2個模態分量：

4）對于k=2，3，...，K，計算第k個殘余分量：

5）再分別對第k個信號Rk（t）+εEk[ni（t）]進行分解，和步驟3）相同分解出第1個模態分量，同時定

義第k+1個模態分量：

6）令k=k+1，執行步驟4），直到最后殘余量不能再被分解時終止分解。最后的殘余量：

原始信號：

1.2 1.5維譜

c（τ，τ）是y（t）的三階累積量c（τ1，τ2）的對角切片，1.5維譜是該對角切片的Fourier變換，即：

其中：Y（ω0）是y（t）的Fourier變換，Y*（ω0）是Y（ω0）的復數共軛。1.5維譜具有如下3個性質：

1）基頻分量加強性質

設振動信號x（t）是均值為零的m次諧波信號，其基頻為ω0，相位為零，當幅值一樣，ωi<ωj時，則：

2）高斯白噪聲的抑制性質

若n（t）為零均值高斯白噪聲，則有：

表明1.5維譜可以有效抑制高斯白噪聲。

3）諧波分量檢測性質

設y（t）為一個諧波信號，ωx、ωy、ωz是y（t）的3個諧波分量，并且ωx>ωy>ωz。若ωx=?ωy+ωz，ωx、ωy、ωz不滿足耦合頻率關系，則有：B（ωx）=B（ωy）=B（ωz）=0;若ωx=ωy+ωz，滿足耦合關系，則有：B（ωx）=?0，B（ωy）=?0，B（ωz）=?0。

這充分說明了經過1.5維譜處理的信號，不存在有3個波形的耦合諧波部分將被消除，存在有3個波形的耦合諧波部分會被提取。

1.3 基于CEEMDAN和1.5維譜的滾動軸承早

期故障診斷方法本文將自適應白噪聲的完備總體經驗模態分解和1.5維譜相結合，提出了一種解決滾動軸承早期故障特征難識別問題的方法，該方法具體實現過程如下：

1）首先利用CEEMDAN將信號分解成一系列IMF分量。

2）根據峭度原則以及相關系數原則選擇一個包含主要故障信息的IMF分量。

3）對提取的IMF分量進行Hilbert解調處理得到其包絡信號。

4）對提取的IMF分量的包絡信號進行1.5維譜分析，得到其1.5維包絡譜。

5）通過分析1.5維包絡譜來判斷軸承的故障類型。

2 仿真信號分析

根據滾動軸承外圈故障機理和其振動數學模型[12-13]，構造強噪背下滾動軸承外圈故障振動信號：

其中，軸承固有頻率fn=3000Hz，位移常數yc=5，阻尼系數φ=0.1，外圈故障特征頻率fo=180Hz，n（t）為噪聲，添加噪聲后信號的信噪比為-8dB，采樣頻率fs=2000Hz，采樣點數N=4096。

圖1（a）為仿真沖擊信號。圖1（b）為染噪后的仿真信號，從圖中可以看出，染噪后的信號十分混亂，沖擊特征已經完全被覆蓋，毫無規律可尋。

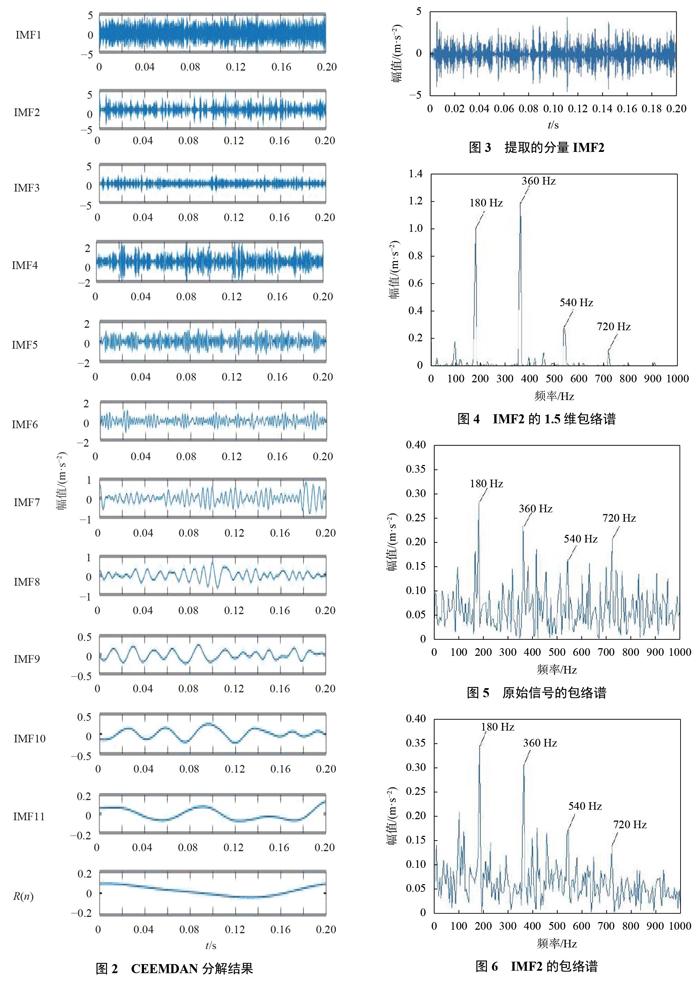
首先，用CEEMDAN對信號進行自適應分解，得到11個IMF分量以及1個殘余分量，如圖2所示。然后根據峭度準則以及相關系數準則提取一個包含主要故障信息的IMF分量作為后續分析對象，本次提取的分量為IMF2。圖3為IMF2的時域圖，從圖中可以看到有比較明顯的周期性沖擊。

最后，對提取的分量IMF2的包絡信號進行1.5維譜分析，得到其1.5維包絡譜如圖4所示。譜圖中清看到與故障特征頻率fo對應的180Hz及其倍頻成分，并且無太多干擾成分，故用此方法成功提取出了故障特征信息。圖5為原始信號的包絡譜，圖6為經過CEEMDAN分解后IMF2的包絡譜，圖7為原始信號的1.5維包絡譜，圖5、圖6、圖7中所表現出的特征提取效果都沒有圖4清。經過對比，凸顯了將這兩種方法結合在早期故障診斷應用上的優勢。

3 實驗分析

本實驗采用美國SpectraQuest公司設計的動力與傳動故障診斷綜合試驗臺，如圖8所示。試驗時，故障軸承安設于靠近電機一側軸承座之上，再安裝3個加速度傳感器于此軸承座上，分別采集垂直、水平以及軸向方向的振動加速度信號，對應圖8中測點1、測點2和測點3，最后通過DT9837型號數據采集儀存儲數據于計算機上。

實驗采用ER-16K型號的深溝球軸承作為實驗對象，為了模擬滾動軸承外圈故障，實驗前保持軸承內圈、滾動體完好，對外圈人為加工輕微凹痕（損傷直徑0.54mm，損傷深度0.26mm）作為軸承外圈早期點蝕故障。實驗所用滾動軸承型號具體結構參數如表1所示。

實驗開始，設置采樣頻率為24000Hz，電機轉速為900r/min（轉頻fr=15Hz），采集數據10s，并取12000個數據點作為后續分析。根據下式計算ER-16K滾動軸承外圈故障特征頻率為53.655Hz。

圖9為本次實驗采集信號的時域波形圖，圖中并沒有發現明顯的周期性沖擊，早期故障微弱，已被強噪聲淹沒。

首先，用CEEMDAN對信號進行自適應分解，得到13個IMF分量以及1個殘余分量。然后根據峭度準則以及相關系數準則提取一個包含主要故障信息的IMF分量，本次提取IMF1作為后續分析對象，如圖10所示。

最后用1.5維譜算法處理提取分量IMF1的包絡信號，得到1.5維包絡譜如圖11所示。譜圖中清顯示出與故障特征頻率相對應的52Hz及其倍頻成分，而且特別清，52Hz與計算所得的滾動軸承外圈故障特征頻率53.655Hz接近，可被認為是外圈故障，至此，本文方法成功提取出了故障特征。作為對比，圖12為IMF1分量的包絡譜;圖13為原始信號的1.5維包絡譜;圖14為原始信號的包絡譜。對比圖11與其他譜圖，圖11故障特征清許多，表明該方法在提取早期故障特征具有一定優勢。

4 結束語

本文研究了基于自適應白噪聲的完備總體經驗模態分解（CEEMDAN）和1.5維譜的滾動軸承早期故障診斷方法。CEEMDAN可以自適應分解復雜信號，與相關系數準則和峭度準則相結合，提取敏感分量，以降低其他頻率的干擾;1.5維譜不僅可以有效抑制白噪聲，提高信噪比，還能增強信號的故障沖擊成分;本文將CEEMDAN與1.5維譜相結合，通過分析仿真信號以及工程實驗數據驗證了該方法在診斷滾動軸承早期故障方面具有一定優勢。

參考文獻

[1]李志星，石博強.自適應奇異值分解的隨機共振提取微弱故障特征[J].農業工程學報，2017，33（11）：60-67.

[2]任學平，王朝閣，張玉皓，等.基于雙樹復小波包自適應Teager能量譜的滾動軸承早期故障診斷[J].振動與沖擊，2017，36（10）：84-92.

[3]王建國，陳帥，張超.噪聲參數最優ELMD與LS-SVM在軸承故障診斷中的應用與研究[J].振動與沖擊，2017，36（5）：72-78.

[4]HUANG N E， SHEN Z， LONG S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non- stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences， 1998， 454（1971）： 903-995. LEI Y， HE Z， ZI Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J]. Mechanical Systems & Signal Processing， 2009， 23（4）： 1327-1338.

[5]LEI Y， ZUO M J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs[J]. Measurement Science & Technology， 2009， 20（12）： 125701. TORRES M E， [5]COLOMINAS M A， SCHLOTTHAUER G， et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//IEEE International Conference on Acoustics， Speech and Signal Processing. IEEE， 2011： 4144- 4147.

[8]張建偉，侯鴿，暴振磊，等.基于CEEMDAN與SVD的泄流結構振動信號降噪方法[J].振動與沖擊，2017，36（22）：138-143.

[9]唐貴基，王曉龍.最大相關峭度解卷積結合1.5維譜的滾動軸承早期故障特征提取方法[J].振動與沖擊，2015，34（12）：79-84.

[10]CHEN L， ZI Y Y， HE Z J， et al. Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method[J]. Journal of Xian Jiaotong University， 2009， 43（5）： 94-98.

[11]鐘先友，曾良才，趙春華.局域均值分解和1.5維譜在機械故障診斷中的應用[J].中國機械工程，2013，24（4）：452-457.

[12]ANTONI J， BONNARDOT F， RAAD A， et al. Cyclostationary modelling of rotating machine vibration signals[J]. Mechanical Systems & Signal Processing， 2004， 18（6）： 1285-1314.

[13]唐貴基，王曉龍.自適應最大相關峭度解卷積方法及其在軸承早期故障診斷中的應用[J].中國電機工程學報，2015，35（6）：1436-1444.