混合流水車間調度問題的果蠅優化算法求解
杜利珍 王 震 柯善富 熊子雪 李新宇
1.武漢紡織大學機械工程及自動化學院,武漢,430073 2.華中科技大學機械科學與工程學院,武漢,430074
0 引言
混合流水車間調度問題(hybrid flow-shop scheduling problem, HFSP)[1]具有現實的制造業背景,涉及多設備、多階段、多工件的加工,屬于NP-hard問題。傳統HFSP可以分為相同并行機[2]、均勻并行機、不相關并行機調度問題[3]。
求解HFSP常用遍歷式算法和啟發式算法。遍歷式算法能夠得到該類問題的精確解,但受限于計算速度,該算法只用于小規模問題的求解[4],而不適用于復雜大系統問題。近年來,啟發式算法的研究不斷取得突破,遺傳算法[5]、蟻群算法[6]、模擬退火算法等相繼被提出并用于求解HFSP,但運算速度還是差強人意,因此人工魚群算法[7]、蜂群算法[8]、二元分布估計算法[9]等一些搜索速度更快、迭代過程更簡單且有效的算法被提出。啟發式算法能夠在短時間內給出大規模問題的解,但這個解在通常情況下是滿意解而非精確解。
編碼與解碼是將模型問題融入算法的一個關鍵過程,編碼決定著輸入,解碼決定著輸出。PAN等[10]提出基于自適應搜索策略的離散人工蜂群算法;王凌等[11]提出基于排列的編碼和解碼的方法,用人工蜂群算法很好地實現了不相關并行機HFSP的求解。
相較于上述算法,果蠅優化算法[12]擁有更好的自適應和自組織能力,具有迭代過程簡單、全局收斂性強、算法執行時間短的特點。筆者在果蠅優化算法的更新規則上加入權重系數,對權重的編碼方式進行改進,使得算法的隨機搜索能力更強,編碼和種群迭代過程更加簡單。
1 不相關并行機混合流水車間調度
1.1 問題描述
不相關并行機HFSP的假設如下:①n個工件在流水線上進行S個階段的加工;②每個階段至少有1臺機器;③至少有一個階段存在并行機;④任意一個階段上的設備都能完成工件的一個工序;⑤工件需要在每個階段完成一道工序;⑥各機器的加工時間不完全相同,已知n個工件各道工序在各設備上的加工時間,要求確定n個工件的加工順序以及每一階段上設備的分配情況,使得某一調度指標最小。混合流水車間調度模型如圖1所示。
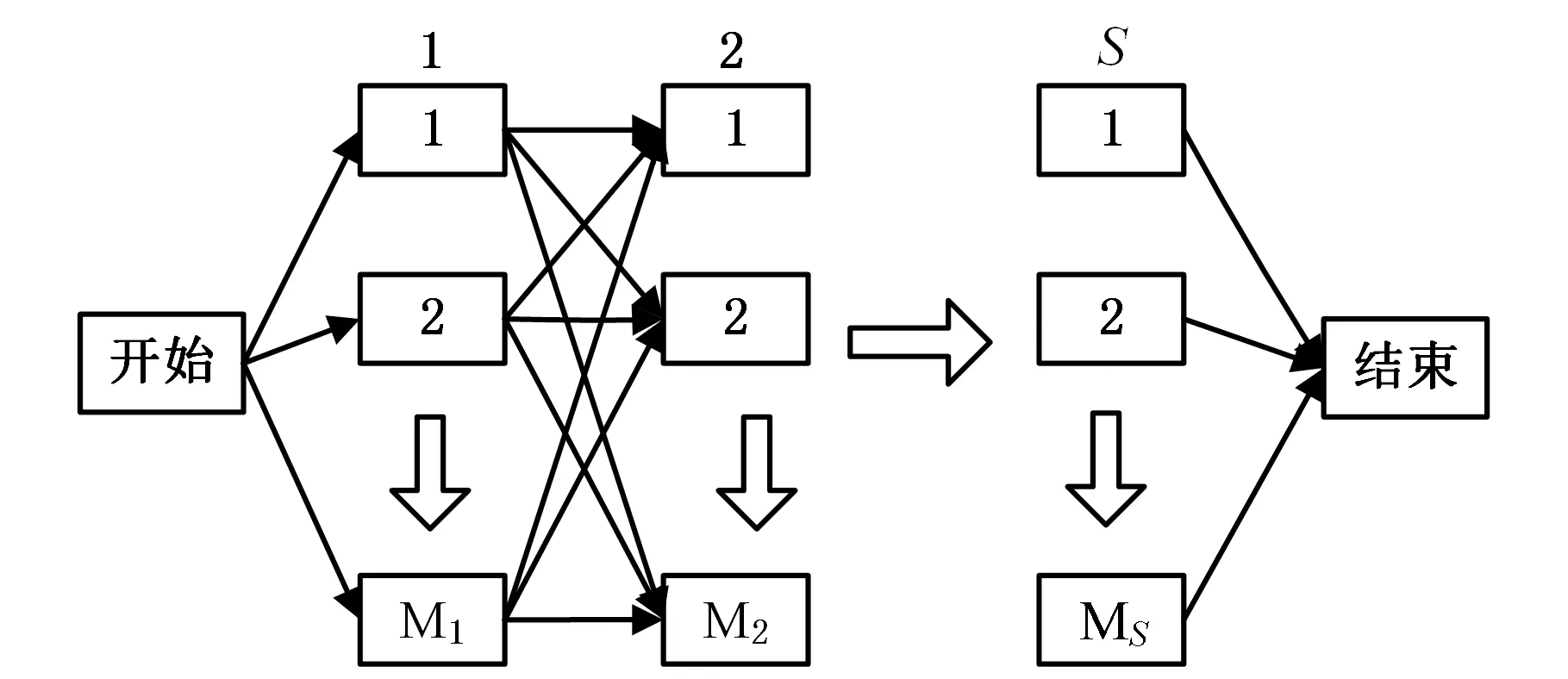
圖1 混合流水車間調度模型Fig.1 Model of hybrid flow-shop scheduling
1.2 數學模型
對于不相關并行機HFSP有:工件的編號為i(i=1,2,…,n);n個工件需要在S個階段上加工;ti,j,k為工件i在第j(j=1,2,…,S)個階段的第k臺設備的加工時間;mj為第j個階段的設備數量;si,j,k為第個i工件在第j個階段的第k臺設備的開始加工時間;Pi,j,k為第i個工件在第j個階段第k臺設備上的加工完成時間;xi,α為0-1變量,工件i被排在第α個位置等待加工時,xi,α=1;Ci為工件Ji的加工完成時間,所有工件加工完成所需的最大完成時間為各工件加工完成時間的最大值,即最大完工時間Cmax=max{C1,C2,…,Cn};L為足夠大的數[13],具體的數字模型如下:
minCmax
(1)

(2)
(3)
(4)
Pi,j,k=si,j,k+ti,j,k
(5)
j=1,2,…,s
Pi,β,k≤si,β+1,k2
(6)
k=1,2,…,mββ=1,2,…,S-1k2=1,2,…,mβ+1
(7)
γ=1,2,…,n-1K=1,2,…,m1
(8)
l1≤l2l1,l2=1,2,…,n
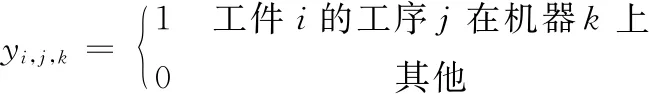
上述公式的含義如下:式(1)為目標函數;式(2)、式(3)保證優先級與工件對應關系的唯一性;式(4)保證工件在任意階段只能在1臺機器上加工;式(5)表示同一階段上工件加工的開始時間和完成時間的關系;式(6)表示工件加工的先后關系;式(7)表示第一階段排序靠前的工件先被加工;式(8)表示如果工件被分配在同一階段的同一設備,排序靠前的工件先加工。不處于同一位置的工件在相同階段的相同設備上加工時,足夠大的數L保證式(8)恒成立。
2 果蠅優化算法
果蠅優化算法利用果蠅覓食的原理不斷進行種群的迭代,最終找到所求問題的最優解。如圖2所示,果蠅優化算法基本步驟如下[14]:
(1)參數初始化。對中心果蠅位置、種群規模、算法迭代次數進行初始化。
(2)嗅覺搜索。在中心果蠅個體的周圍產生其他果蠅個體,計算種群每個果蠅個體的適應度,用于評價每個果蠅個體。
(3)視覺搜索。選擇適應度最大的果蠅作為下一次迭代的種群中心,利用種群更新公式進行新一代種群更新。

圖2 改進果蠅優化算法流程圖Fig.2 Framework of the improved FOA
(4)判斷是否滿足迭代終止條件。若滿足則結束迭代,輸出最優結果;否則轉至步驟(2)。
3 果蠅優化算法的求解
3.1 編碼
本文采用基于權重的編碼方式,將離散系統的求解轉化成連續系統的求解。工件的加工順序根據權重的大小依次排列,每種排列表示一個可行解,例如權重(0.20,0.18,0.36,0.25,0.64,0.57)對應的工件排列順序為(5,6,3,4,1,2),該排序表示工件5先加工,其次是工件6,最后是工件2。這種編碼方式能夠便于種群的更新操作。
3.2 解碼
解碼采用基于排列的方式[15],主要分為工件的排序和設備的選擇。工件排序的規則:第一階段,按照初始的工件排序依次進行加工,后面階段的工件按照前一階段加工完成時間先后順序進行加工;多個工件的加工完成時間相同時,隨機選擇其中一個工件進行加工。設備的選擇規則:根據工件i在階段j上的加工順序,判斷每個工件在第k臺設備上的最早允許加工時間,即設備k釋放時間Pk與工件i在上一階段的完成時間Ri,j-1的較大者max(Pk,Ri,j-1);然后對工件i根據公式max(Pk,Ri,j-1)+ti,j,k選擇值小的機器k作為工件i的加工設備。重復以上步驟直到所有工件完成S個階段的加工。
3.3 種群初始化
初始化種群規模psize,采用產生隨機數的方式來產生初始解Qz,根據Qz對工件的加工進行排序。矩陣Qz的元素是0~1之間的隨機數,可保證初始解的隨機性。
3.4 嗅覺操作
通過產生隨機數的方式產生與初始解相同維度的隨機數矩陣Ly,則果蠅種群X(i)=Qz+Ly,對種群中的每一個果蠅個體X(i)以最大完成時間最小作為評價指標進行計算。單目標適應度函數為
F(x)=minCmax
(9)
果蠅優化算法種群初始化及嗅覺操作偽代碼如下。
輸入:工件在各機器上的加工時間表
輸出:最優的排序
Gj=[1,2,3,4,5,6];
∥工件排序
Sizepop=5;
∥初始化種群個數
K=6;
∥種群個體維度
Qz=rand(1,k);
∥隨機初始種群中心權重
FOR i=1:sizepop;
X(i)=B1Qz+B2normrnd;
∥種群權重
END FOR
FOR i=1:sizepop
a=[Gj’,X(i,:)];
∥工件順序按照權重重排
F(i)=f(a);
∥計算種群個體適應度
Besta=arg min(F(i));
∥選擇適應值最小的排序
END FOR
3.5 視覺操作
選取嗅覺操作中的最優果蠅個體作為下一個種群的中心果蠅,其他果蠅向該果蠅移動,從而產生新的種群。種群的更新方式與嗅覺操作方式相同,改進果蠅優化算法更新規則為
X(i)=B1Qbest+B2Nr
(10)
式中,B1表示果蠅中心對果蠅種群的影響程度;B2表示種群領域隨機搜索能力對種群的影響程度;X(i)(i=1,2,…,psize)為果蠅個體權重矩陣,幾何上表示果蠅個體位置,下同;Qbest為中心果蠅權重矩陣;Nr為隨機權重矩陣。
與原始算法更新公式X(i)=Qbest+Nr相比,改進后的更新公式增加了變量B1、B2,提高了算法的隨機搜索能力。
4 仿真測試和比較
標桿實例1[16]12個工件的加工工序為車、刨、磨,現有3臺車床、2臺刨床、4臺磨床,每臺機床的加工能力不同,工件在設備M1~M9上的加工時間如表1所示。

表1 實例1加工時間表
標桿實例2[17]某工廠需要加工6個工件,每個工件都需要經過銑、車、磨三道工序。現有3臺銑床、2臺車床、3臺磨床,設備用M1~M8表示。工件的加工時間如表2所示。
標桿實例3[18]某鋼鐵生產包含煉鋼、精煉、連鋼、軋制四個步驟,完成這些工序需要3臺煉鋼爐、3臺精煉爐、2臺鑄機、2臺軋機,用M1~M10表示。工件在設備上的加工時間如表3所示。

表2 實例2加工時間表

表3 實例3加工時間表
4.1 參數討論
對該果蠅優化算法的種群規模psize、中心果蠅重要程度參數B1、隨機搜索能力參數B2進行測試。將評價次數3 000作為每種參數組合運行的終止條件,對每一種參數組合獨立運行20次,程序使用MATLAB編程,在4G內存、3.20 GHz CPU上運行,得到最大完成時間的平均值和標準差,如表4所示。

表4 實例1參數組合
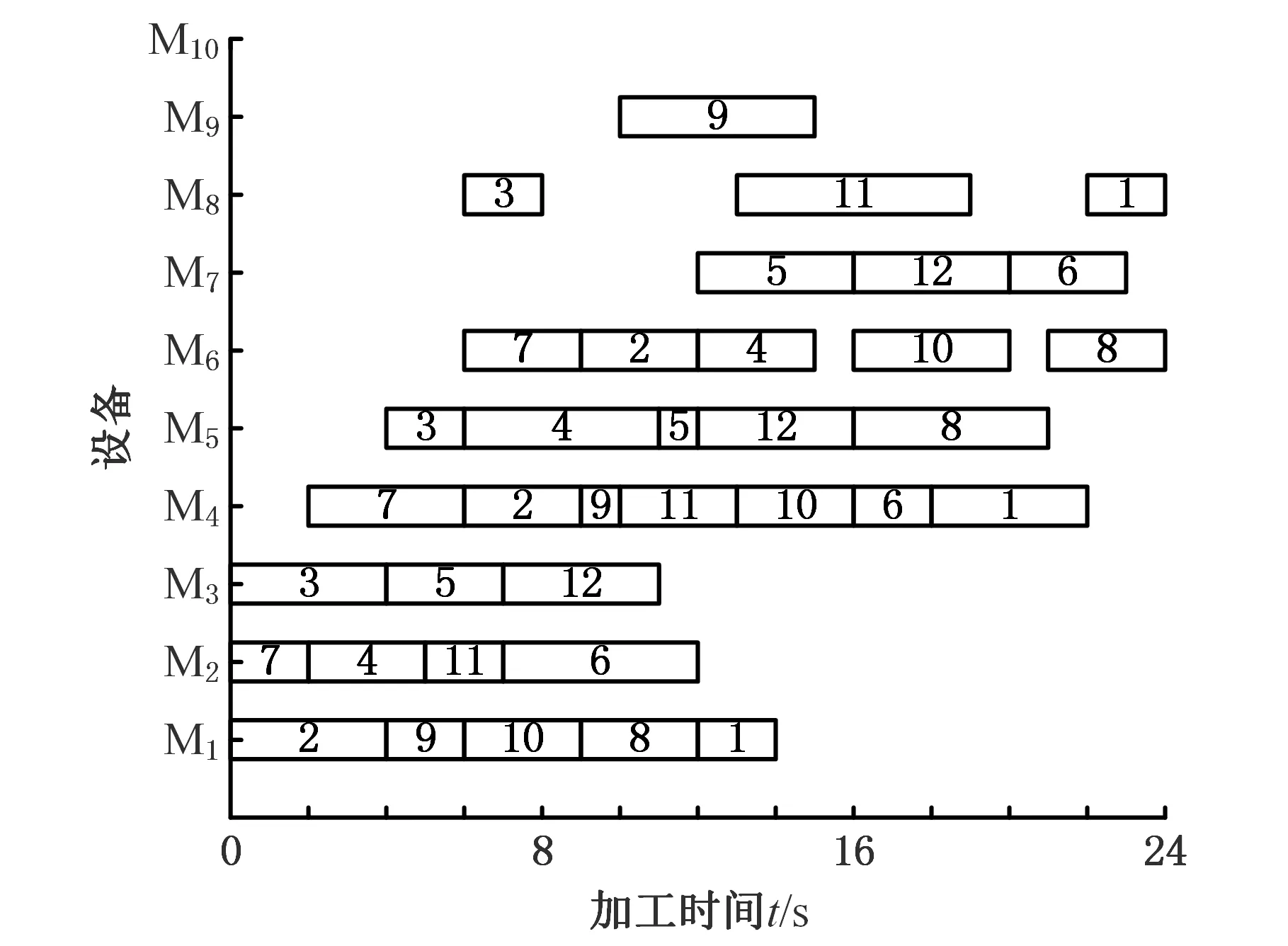
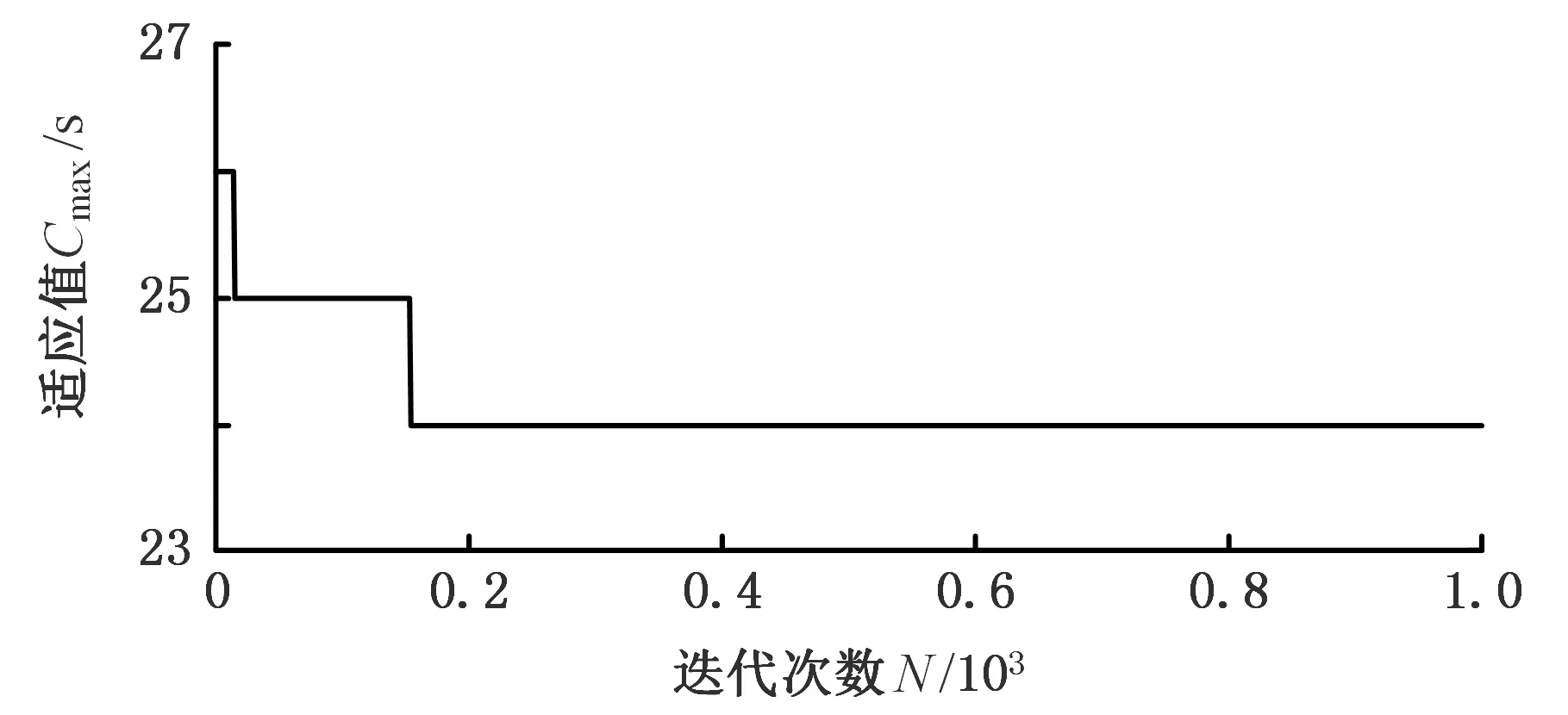
統計實例1在不同參數組合條件下運行時的均值和極值,如圖3所示。以標桿案例1為例,對算法參數進行分析可知,B1 圖3 實驗結果圖Fig.3 Experiment results chart 對實例2在2 000次評價,實例3在6 000次評價的條件下設計同樣的實驗,得到3種規模的最優參數組合,如表5所示。 表5 實例1參數組合 為了進一步說明果蠅優化算法(fruit fly optimization algorithm,FOA)的優越性,將該算法與遺傳算法(GA)[16]和差分進化(differential evolution,DE)算法[18]進行對比。將評價次數10 000作為算法運行終止條件,得到的結果如表6所示。文獻[16]給出了一種改進的編碼方式,這種編碼方式能夠保證個體編碼的合法性。文獻[18]通過特殊的編碼方案,結合基于DE算法的進化搜索和局部搜索,增強探索和開發能力。 表6 實例1結果比較 由表6可以看出,GA不夠穩定,未能找到最優解24,DE算法能8次找到最優解24,而FOA能夠100%找到最優解24,因此在相同的評價次數中,FOA的穩定性更好,其最優解甘特圖為圖4,圖中方框內的數據為工件序號,收斂曲線如圖5所示。 圖4 最優調度的甘特圖Fig.4 Gantt chart of the optimal solution 圖5 收斂曲線圖Fig.5 Convergence curve chart 實例2的實驗結果對比如表7所示,將FOA與PBIL[17](population-based incremental learning)、EDA[17](estimation of distribution algorithm)進行對比。將評價次數3 000作為算法運行終止條件。在相同評價次數中,FOA能100%找到最優解13.5,其他2個算法沒能找到最優解,從而驗證了算法的有效性和魯棒性。實例3的實驗結果對比如表8所示,將評價次數18 000作為算法運行終止條件,10次獨立運行中,FOA能6次找到最優解297,且結果優于DE算法的結果[19],再一次證明了算法了有效性。 表7 實例2結果比較 表8 實例3結果比較 在原始果蠅優化算法的基礎上,增加了中心果蠅影響程度參數B1和領域搜索能力參數B2,通過實驗考察了2個參數對算法的影響。在相同的實驗條件下,改進果蠅優化算法更容易找到最優解,且不容易陷入局部最優。與GA、EDA、DE算法進行對比,改進果蠅優化算法表現出了極好的隨機搜索能力和魯棒性。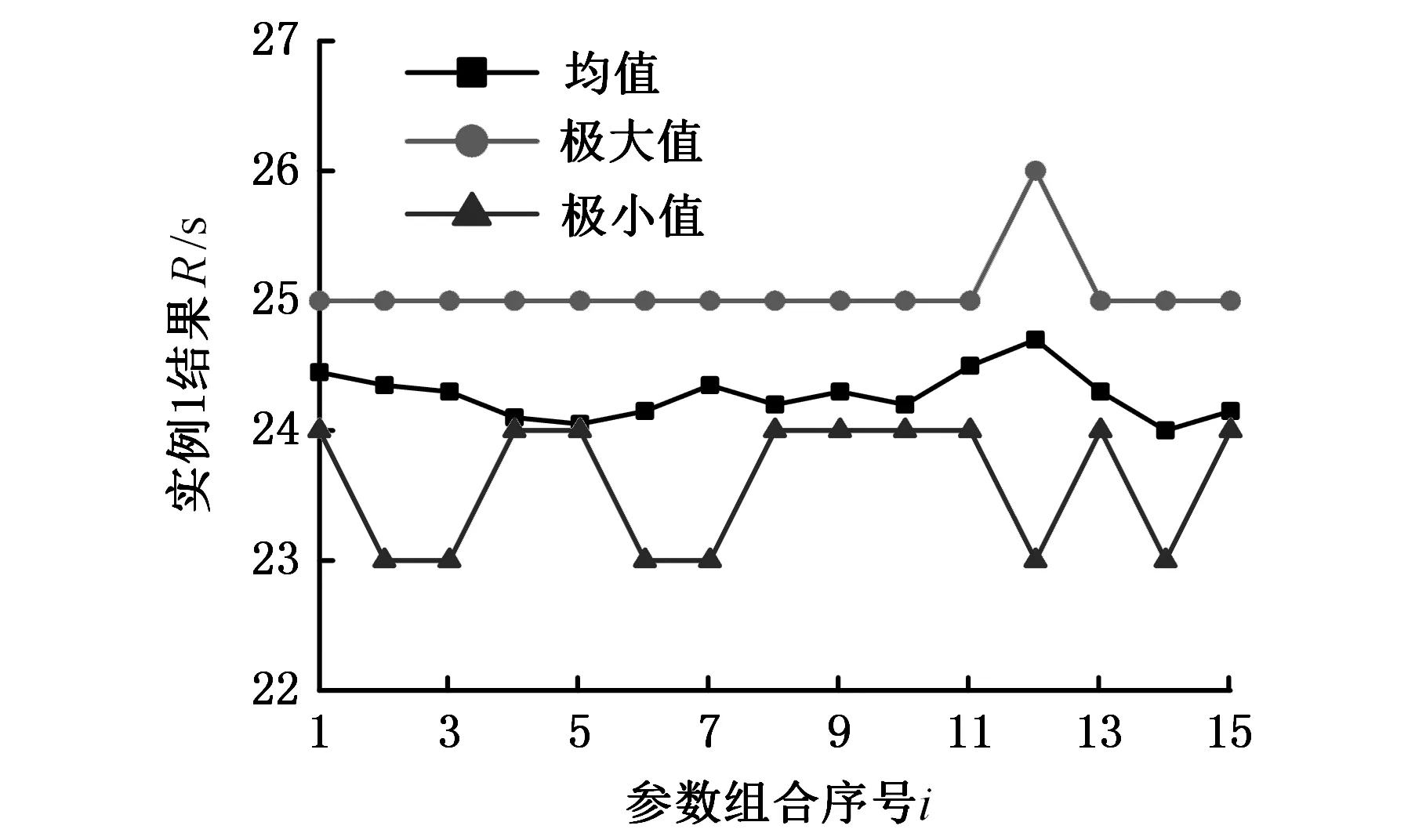
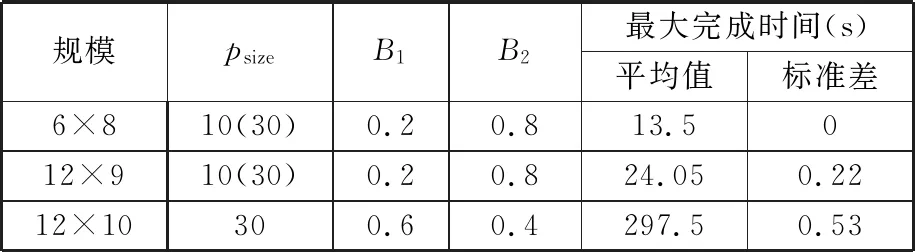
4.2 實驗結果對比



5 結論

