解析型Timoshenko梁有限單元

許 晶 ，李世堯 ,2，王斌泰 ，李 靜 ,3，蔣秀根

（1.中國(guó)農(nóng)業(yè)大學(xué)水利與土木工程學(xué)院，北京 100083；2.杭州電子科技大學(xué)通信工程學(xué)院，浙江 杭州 310018；3.河南職業(yè)技術(shù)學(xué)院環(huán)境藝術(shù)工程系，河南 鄭州 450046）

深梁指跨高比較小的梁.深梁是常存在于筏板基礎(chǔ)、深基坑支護(hù)結(jié)構(gòu)、高層建筑中的轉(zhuǎn)換梁、框筒結(jié)構(gòu)中的梁，基于結(jié)構(gòu)安全和經(jīng)濟(jì)角度考慮，提出一種對(duì)此類構(gòu)件的受力性能進(jìn)行精確且高效分析的計(jì)算方法很有必要.

分析梁的兩個(gè)常用基本理論為Euler-Bernoulli梁理論和Timoshenko 梁理論.基于Euler-Bernoulli梁理論，很多學(xué)者[1-4]對(duì)梁構(gòu)件進(jìn)行了受力分析并提出了各類模型，但是這些研究中均未考慮梁的剪切變形.文獻(xiàn)[5-6]研究發(fā)現(xiàn)，計(jì)算深梁內(nèi)力時(shí)不考慮剪切變形影響會(huì)導(dǎo)致結(jié)構(gòu)或構(gòu)件內(nèi)力計(jì)算結(jié)果偏低，故基于Euler-Bernoulli 梁理論提出的計(jì)算模型不能對(duì)深梁受力性能進(jìn)行精確分析.

針對(duì)深梁，各國(guó)學(xué)者提出了多種理論，其中Timoshenko[7]于1921年提出的兩廣義位移梁理論得到廣泛應(yīng)用.該理論認(rèn)為變形前垂直于直梁中心線的截面在變形后仍保持為平面，但不再假定它一定垂直變形后的中心線，即變形后截面轉(zhuǎn)角與梁軸線轉(zhuǎn)角不再相等，兩者之差為剪切角.基于Timoshenko梁理論，一些學(xué)者采用靜力法和能量法對(duì)梁進(jìn)行了研究，但這些理論方法可精確解決受力簡(jiǎn)單梁內(nèi)力和位移的計(jì)算問(wèn)題，對(duì)于存在移動(dòng)荷載和多種荷載共同作用的復(fù)雜結(jié)構(gòu)或構(gòu)件分析，靜力法和能量法無(wú)法得到滿意解.利用深梁理論構(gòu)造單元時(shí)，最為關(guān)鍵的問(wèn)題是確定剪切修正系數(shù).剪切修正系數(shù)有多種計(jì)算理論和方法[8-10]，但這些系數(shù)是對(duì)不同截面的剪應(yīng)力分布或梁的本構(gòu)關(guān)系采用不同假定得出的，這些假定對(duì)簡(jiǎn)單截面計(jì)算結(jié)果相同，對(duì)復(fù)雜截面計(jì)算的剪切修正系數(shù)不同.

數(shù)值計(jì)算法中的有限元法[11]以效率更高、適用性更廣、精度可以滿足工程要求被很多學(xué)者用于梁構(gòu)件受力性能分析中.實(shí)際分析中，常采用插值形函數(shù)法構(gòu)造的梁?jiǎn)卧獙?duì)梁受力及變形進(jìn)行分析.基于Timoshenko 梁理論，不同學(xué)者利用線性插值、二次插值、多次插值等方法構(gòu)造了深梁?jiǎn)卧猍11-12]，由于這些插值函數(shù)為位移的近似方程，計(jì)算結(jié)構(gòu)存在截?cái)嗾`差，計(jì)算精度較低.為取得較好計(jì)算精度，須采取多單元，加密節(jié)點(diǎn)的技術(shù)，則必然造成計(jì)算效率的降低.文獻(xiàn)[13-16]考慮剪切變形對(duì)沿桿長(zhǎng)方向的內(nèi)力和位移影響，提出了構(gòu)建桿件單元解析形函數(shù)的一般理論，并構(gòu)造出一系列解析型單元，通過(guò)與插值形函數(shù)構(gòu)造的單元對(duì)比發(fā)現(xiàn)，該解析型單元的計(jì)算精度更好，效率更高.

本文以深梁為研究對(duì)象，以Timoshenko 梁理論和有限元法為基礎(chǔ)，利用Timshenko 梁基本方程建立了深梁位移控制方程，進(jìn)而構(gòu)建了梁撓度、截面彎曲轉(zhuǎn)角和剪切角的解析位移形函數(shù).基于勢(shì)能原理和解析位移形函數(shù)，構(gòu)造了解析型深梁?jiǎn)卧?通過(guò)計(jì)算懸臂梁、簡(jiǎn)支梁的端部撓度和轉(zhuǎn)角，將本單元與理論解、插值形函數(shù)計(jì)算的結(jié)果進(jìn)行對(duì)比，驗(yàn)證了本解析型單元的高精度、高效性.

1 參數(shù)及控制方程

1.1 位移內(nèi)力參數(shù)

如圖1所示，深梁總長(zhǎng)度為l，梁上荷載有：節(jié)點(diǎn)A、B 兩端分別受彎矩MA、MB；剪力VA、VB；梁上集中力矩Mi、分布彎矩mi、 橫向集中荷載Pi、均布荷載qy，其中，i為橫向坐標(biāo)點(diǎn).梁上位移有：撓度v；梁兩端軸線轉(zhuǎn)角 φA、 φB.所有荷載和位移（撓度、轉(zhuǎn)角）與坐標(biāo)軸方向一致為正；當(dāng)截面法線與坐標(biāo)方向一致時(shí)，深梁內(nèi)力與坐標(biāo)方向一致時(shí)為正，反之為負(fù).

如圖2所示，深梁的位移變量有：v；彎曲撓度vM；剪切撓度vV；截面彎曲轉(zhuǎn)角θ；截面剪切角 γ；梁軸線轉(zhuǎn)角 φ.

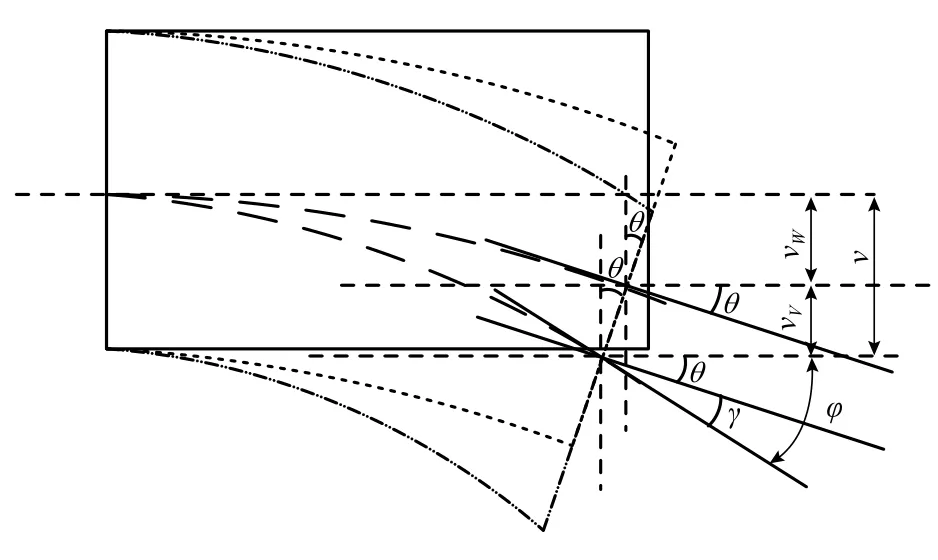
圖2 梁微段變形圖Fig.2 Deformation of beam micro segment

梁?jiǎn)卧淖杂啥龋汗?jié)點(diǎn)A、B 共有4 個(gè)自由度，節(jié)點(diǎn)位移向量其中，vA、vB為梁節(jié)點(diǎn)A、B 的撓度，θA、 θB為梁節(jié)點(diǎn)A、B 的截面轉(zhuǎn)角；單元的節(jié)點(diǎn)力向量

1.2 基本方程

1.2.1 幾何方程

梁軸線轉(zhuǎn)角方程為

轉(zhuǎn)角關(guān)系方程為

截面曲率方程為

1.2.2 平衡方程

力矩平衡方程為

式中：M（x）、V（x）表示沿深梁桿長(zhǎng)任意截面的彎矩、剪力.

剪力平衡方程為

1.2.3 物理方程

彎曲剛度方程為

式中：E為材料彈性模量；I為深梁截面慣性矩.

剪切剛度方程為

式中：G為材料剪切模量；A為截面面積；k為截面不均勻剪切系數(shù)[17]，，S為面積矩，b為截面寬度.

1.3 位移控制方程

1.3.1 撓度控制方程

由式（4）～（6），可得

由式（1）～（3）和式（7）可得

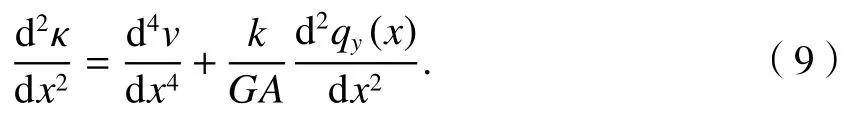
聯(lián)立式（8）、（9）可得撓度控制方程為

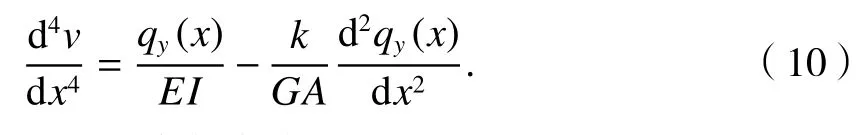
1.3.2 剪切角控制方程

由式（4）、（5）和式（7）可得剪切角控制方程為

1.4 位移協(xié)調(diào)方程

由式（1）～（7）可得撓度與剪切角的協(xié)調(diào)方程為

2 單元位移方程

2.1 控制方程求解

2.1.1 撓度控制方程求解

為了建立深梁?jiǎn)卧膿隙刃魏瘮?shù)，不考慮梁上的分布荷載，撓度微分控制方程（10）簡(jiǎn)化為齊次方程，對(duì)其求解，可得撓度為

式中：f為撓度基函數(shù)向量，為位移系數(shù).

2.1.2 剪切角控制方程求解

為了建立深梁?jiǎn)卧募羟薪切魏瘮?shù)，不考慮梁上的分布荷載，剪切角微分控制方程（11）簡(jiǎn)化為齊次方程，對(duì)其求解，可得剪切角為

式中：c5為位移系數(shù).

2.2 位移協(xié)調(diào)條件的應(yīng)用

將撓度方程（13）、剪切角方程（14）代入?yún)f(xié)調(diào)方程式（12），可得，剪切角可變?yōu)?/p>

式中：g為剪切角基函數(shù)向量[18]，

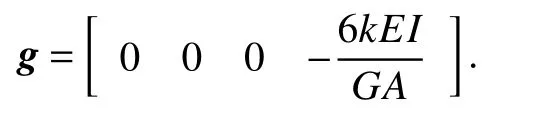
由軸線轉(zhuǎn)角方程（1）、轉(zhuǎn)角關(guān)系方程（2）和撓度方程（13），截面彎曲轉(zhuǎn)角可表示為

式中：h為截面轉(zhuǎn)角基函數(shù)向量[18]，

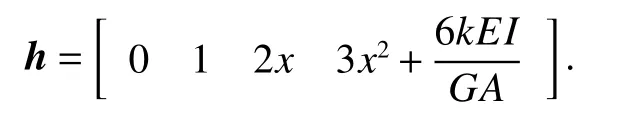
3 單元位移形函數(shù)

3.1 位移系數(shù)定解

由撓度方程（13）和截面轉(zhuǎn)角方程（16）及節(jié)點(diǎn)位移向量表達(dá)式，有

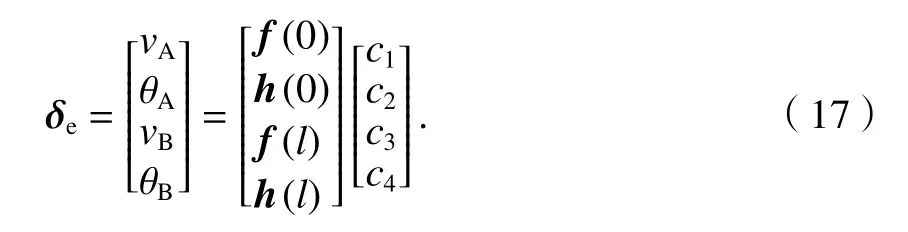
則式（17）用矩陣形式可表示為

位移系數(shù)可表達(dá)為

則有

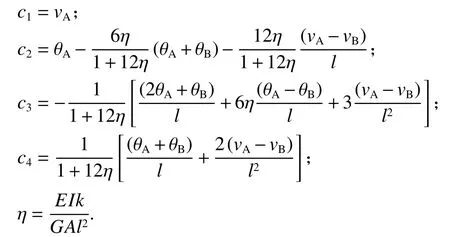
顯然，當(dāng)不考慮剪切變形時(shí)，深梁直接退化為淺梁，剪切剛度GA取為無(wú)窮大，則η 取為0.

3.2 單元位移形函數(shù)

3.2.1 撓度v位移形函數(shù)

由式（13）、（19），可得

由位移形函數(shù)的定義v(x)=Nvδe，可得

3.2.2 截面轉(zhuǎn)角θ 位移形函數(shù)

由式（16）、（19）可得

由位移形函數(shù)的定義θ (x)=Nθδe，可得

3.2.3 剪切角 γ位移形函數(shù)

由式（15）、（19）可得

由位移形函數(shù)的定義 γ=Nγδe，可得

4 Timoshenko 梁?jiǎn)卧惺?/h2>

4.1 單元?jiǎng)菽?/h3>

4.1.1 變形能

單元的變形能為桿件彎曲變形能UM和剪切變形能UV之和，其表達(dá)式用位移形函數(shù)形式表示為

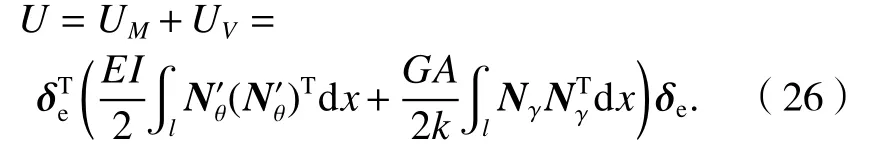
4.1.2 荷載勢(shì)能

梁的荷載勢(shì)能由節(jié)點(diǎn)力勢(shì)能、梁上豎向均布荷載勢(shì)能、豎向集中力及力矩勢(shì)能組成，其表達(dá)式用位移形函數(shù)形式表示為

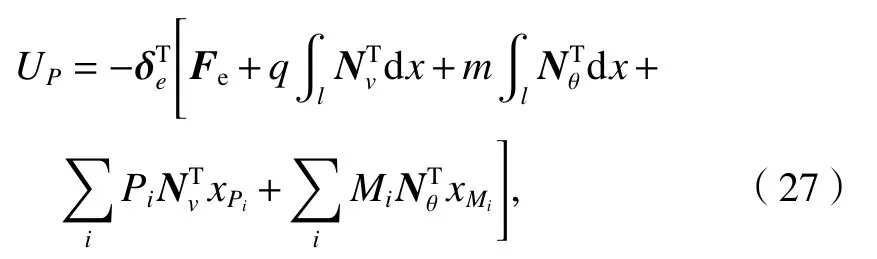
式中：xPi為 橫向集中荷載Pi的 作用點(diǎn)位置；xMi為為集中力矩Mi的作用點(diǎn)位置.

4.1.3 總勢(shì)能

單元總勢(shì)能為

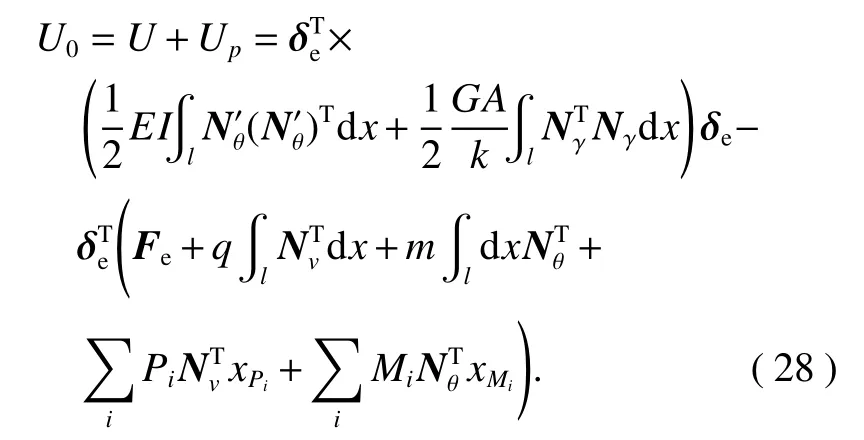
4.2 單元列式

根據(jù)勢(shì)能變分原理，真實(shí)的結(jié)構(gòu)位移必然使得單元的勢(shì)能最小，即對(duì)深梁?jiǎn)卧鎸?shí)的節(jié)點(diǎn)位移必然滿足由式（28）可得

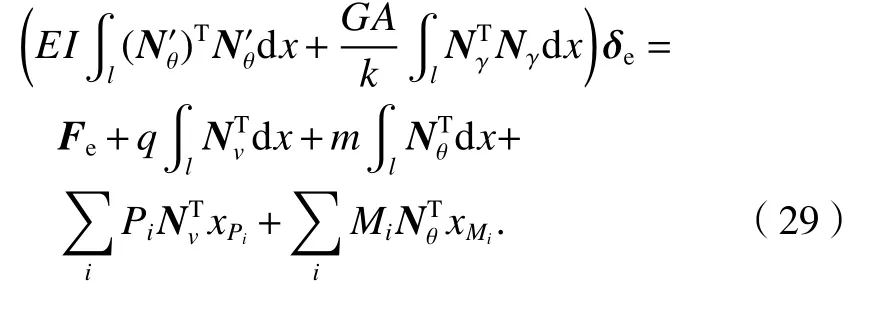
式（29）可簡(jiǎn)寫為

式中：Ke為 單元總剛度矩陣，Ke=KM+KV，KM為彎曲剛度矩陣，其表達(dá)式見(jiàn)文獻(xiàn)[18]，KV為剪切剛度矩陣，其表達(dá)式見(jiàn)文獻(xiàn)[18]；為等效荷載向量.

4.3 等效節(jié)點(diǎn)力

梁上均布荷載等效節(jié)點(diǎn)力向量為

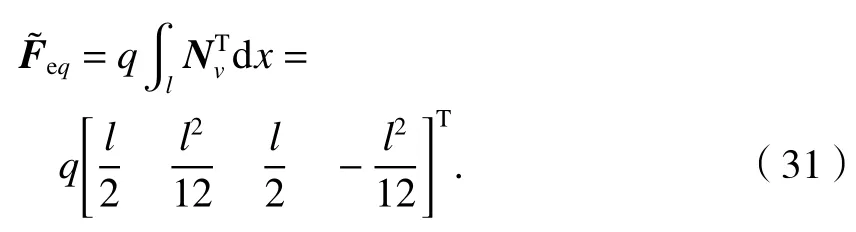
梁上分布力矩等效節(jié)點(diǎn)力向量為

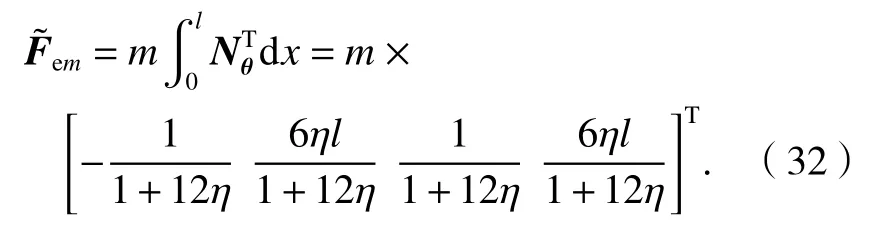
梁上集中力等效節(jié)點(diǎn)力向量為

梁上集中力矩等效節(jié)點(diǎn)力向量為

4.4 關(guān)于適用性的討論

由KM和KV表達(dá)式可得考慮剪切變形影響的單元總剛度矩陣，具體表達(dá)式為

不考慮梁的剪切應(yīng)變，剪切剛度GA取為無(wú)窮大，則η 取為0，式（35）可變?yōu)?/p>

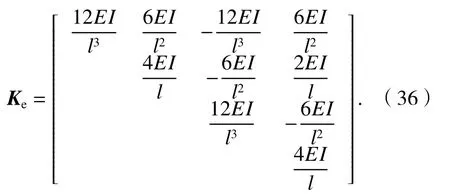
式（36）同Euler 梁?jiǎn)卧獎(jiǎng)偠染仃囈恢耓16]，由此可見(jiàn)，本文構(gòu)造的單元總剛度矩陣可退化為Euler梁?jiǎn)卧獎(jiǎng)偠染仃嚕也淮嬖诩羟虚]鎖問(wèn)題.

5 算例與對(duì)比

為驗(yàn)證基于Timoshenko 梁理論，采用解析形函數(shù)法構(gòu)造的梁?jiǎn)卧木_性，分別采用理論解、插值形函數(shù)法、解析形函數(shù)法求解懸臂深梁和簡(jiǎn)支深梁的端部位移，并進(jìn)行對(duì)比；為驗(yàn)證剪切變形對(duì)深梁位移影響，將Euler 梁?jiǎn)卧cTimoshenko 梁?jiǎn)卧?jì)算結(jié)果進(jìn)行對(duì)比.

5.1 桿件參數(shù)

圖3為懸臂梁和簡(jiǎn)支梁受力簡(jiǎn)圖.假定兩種梁的截面尺寸均為2 m × 3 m，梁長(zhǎng)均為9 m，材料彈性模量E=210 GPa，剪切模量G= 80 GPa，不均勻剪切系數(shù)k= 2/3.懸臂梁和簡(jiǎn)支梁所受的荷載工況：（1）右端集中力100 kN；（2）左端和右端集中彎矩500 kN·m；（3）滿跨均布荷載40 kN/m2.

圖3 梁構(gòu)件Fig.3 Beam

5.2 結(jié)果與分析

不劃分單元，采用解析形函數(shù)法計(jì)算懸臂梁和簡(jiǎn)支梁端部位移，并與理論解、插值形函數(shù)法的計(jì)算結(jié)果進(jìn)行對(duì)比，采用Euler梁?jiǎn)卧蚑imoshenko 梁?jiǎn)卧?jì)算的懸臂梁和簡(jiǎn)支梁結(jié)果對(duì)比見(jiàn)表1、2.對(duì)于懸臂梁，左端為固定端，故左端撓度 νA和 轉(zhuǎn)角 θA為0；對(duì)于簡(jiǎn)支梁，兩端為簡(jiǎn)支，故兩端撓度 νA和 νB均為0.

由表1、2 可知，在單元數(shù)量相同時(shí)，采用解析形函數(shù)法構(gòu)造的梁?jiǎn)卧谟?jì)算撓度和轉(zhuǎn)角精度上高于插值形函數(shù)法構(gòu)造的單元，這是由于本文構(gòu)造的解析型單元基于解析位移形函數(shù)模式，很大程度消除了模型誤差帶來(lái)的影響.同時(shí)，該解析型單元不需要?jiǎng)澐謫卧纯傻玫脚c理論解一致的計(jì)算結(jié)果.

對(duì)于懸臂梁，承受均布荷載作用時(shí)，基于Euler梁計(jì)算的位移與基于Timoshenko 梁理論構(gòu)造的解析型單元計(jì)算的梁端位移偏差可達(dá)到50.000%；承受右端集中彎矩作用時(shí)，計(jì)算的位移偏差較小.對(duì)于簡(jiǎn)支梁，承受均布荷載作用時(shí)，基于Euler 梁計(jì)算的位移與基于Timoshenko 梁理論構(gòu)造的解析型單元計(jì)算的梁端位移偏差為0.001%；承受端部集中彎矩作用時(shí)，計(jì)算的位移偏差可達(dá)到10.769%.

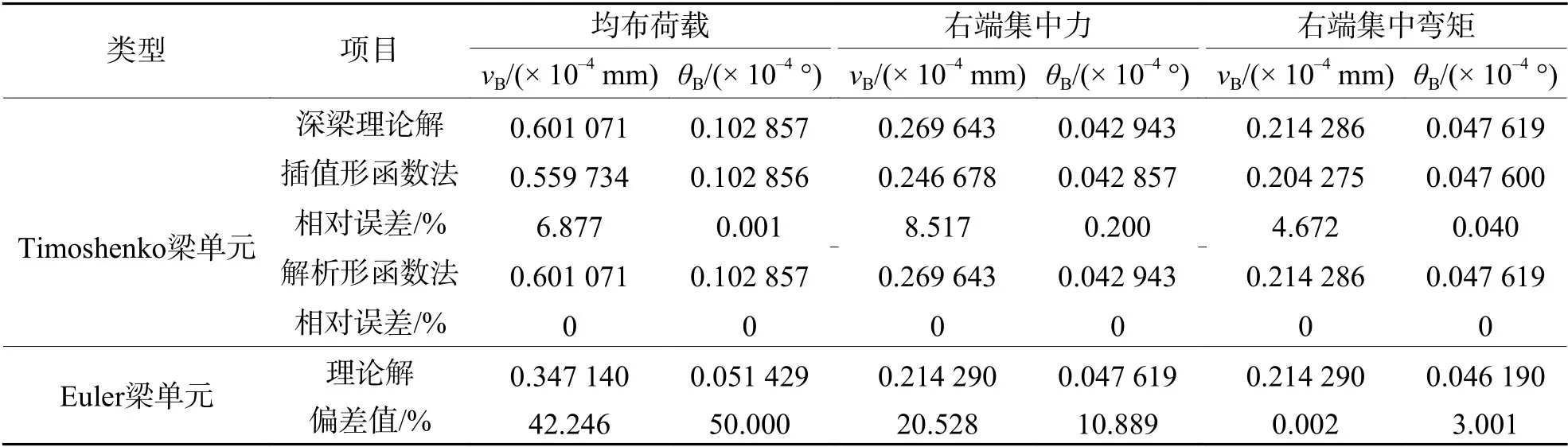
表1 懸臂梁端部位移計(jì)算結(jié)果對(duì)比Tab.1 Comparisons of end displacement for cantilever beam

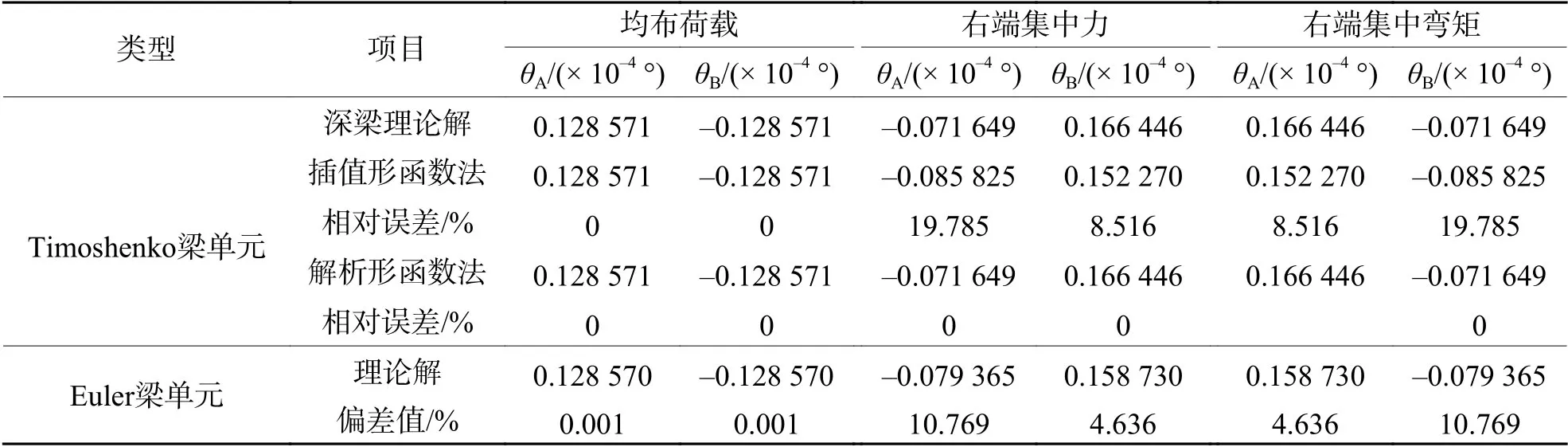
表2 簡(jiǎn)支梁端部轉(zhuǎn)角計(jì)算結(jié)果對(duì)比Tab.2 Comparisons of end bending angle for simply supported beam

6 結(jié) 論

基于Timoshenko 梁基本方程，建立了深梁位移控制方程，構(gòu)造了深梁?jiǎn)卧獜澢鷵隙取⒔孛孓D(zhuǎn)角和剪切角的解析位移形函數(shù)；利用勢(shì)能變分原理，結(jié)合解析位移形函數(shù)，構(gòu)造了解析型深梁?jiǎn)卧⒔o出了解析型深梁?jiǎn)卧倓偠染仃嚕挥蓜?shì)能泛函變分，得到均布荷載、集中力、分布力矩、集中力矩等荷載下的等效節(jié)點(diǎn)力.結(jié)合單元位移形函數(shù)，可得各種復(fù)雜荷載下深梁的節(jié)點(diǎn)位移.本文構(gòu)造的解析型單元計(jì)算深梁撓度和轉(zhuǎn)角的精度遠(yuǎn)高于插值形函數(shù)單元，且采用一個(gè)單元即可保證計(jì)算結(jié)果與理論解一致，滿足了高精度、高效率的要求；構(gòu)造的深梁?jiǎn)卧捎糜贓uler 梁結(jié)構(gòu)分析，且不存在剪切閉鎖問(wèn)題.