基于粒子濾波聯(lián)合算法的地磁室內定位

黃 鶴 ，仇凱悅 ，李 維 ，羅德安

（1.北京建筑大學測繪與城市空間信息學院，北京 102616；2.北京建筑大學北京未來城市設計高精尖創(chuàng)新中心，北京 100044）

在諸多建筑物的室內環(huán)境中，獲得高精度的位置信息是一項具有挑戰(zhàn)性的任務.由于衛(wèi)星信號的衰減，傳統(tǒng)方法（如GPS）在建筑物內部無法正常工作，這促進了室內定位系統(tǒng)的快速發(fā)展，例如基于WiFi[1]，ZigBee[2]和RFID[3]的室內定位系統(tǒng).然而，當使用無線電技術來解決室內定位問題時，物理障礙物產生的影響無法避免，會對定位系統(tǒng)接收信號產生干擾.此外，上述提出的室內定位解決方案的另一個需要解決的問題是都需要部署特定設備或在定位過程中使用額外的硬件，并且基礎設備需要定期維護，這些都需要高昂費用.

因此，無需額外設備投入的地磁定位技術備受關注.地磁場通常用于確定設備的航向[4].然而，室內環(huán)境中的重大磁擾動往往會對定向估計的準確性造成不利影響.通常需要校準，但這不是一件容易的事情.另一方面，建筑物中的混凝土與鋼結構以及磁性鐵質設備對室內地磁場造成的形變，可以被視為信息源.因此可以利用室內磁場的局部異常來獲取室內各個位置的獨特標記，采用類似“指紋”的方式構建參考圖，而且室內地磁場在幾周甚至幾個月的時間尺度上具有穩(wěn)定性[5-6].

早在2000年，Suksakulchai 等[7]認識到磁場干擾可以用于室內定位.在進行室內地磁定位時，需要已知的地磁參考圖.雖然同時定位和建圖（SLAM）技術克服了這個問題[8]，但大多數相關工作主要集中在解決匹配定位上，匹配算法通常是采用粒子濾波算法（particle filter，PF）.文獻[8]結合智能手機中的慣性傳感器，以航跡推算算法作為粒子濾波器的運動模型，利用測量磁場的總強度更新粒子權重，兩條走廊之間的角落則被用作位置矯正的地標，同時對匹配區(qū)域的范圍進行約束，在實驗中實現(xiàn)了小于1 m 的定位精度.文獻[9]中，利用現(xiàn)有的地磁參考圖和地磁傳感器的測量信息用粒子濾波器進行定位.實驗表明，相比于只用磁場總強度，若同時考慮磁場的3 個分量會使得定位精度更高，在小區(qū)域的室內定位中可以達到厘米級.文獻[10]提出了一種在粒子濾波器的實現(xiàn)中使用慣性傳感器并應用磁場圖和室內地圖的方法，以提高定位和跟蹤的準確性；使用梯度下降法來糾正由于磁擾動引起的用戶航向估計問題；使用磁場三分量加室內地圖的實驗實現(xiàn)了0.75 m的平均定位精度，標準偏差為0.52 m.

現(xiàn)有基于粒子濾波算法的室內地磁定位中大多是以點為匹配單元，基于點的匹配模式一共有3 種組合（磁場強度；水平分量和垂直分量；x、y、z軸分量），一個點的地磁匹配特征最多只有3 個.如果只依靠磁場測量值，在地磁匹配中會導致定位結果模棱兩可[11].增加匹配特征的數量是一個解決方法，因此本文提出基于路徑的匹配模式，由多點構成的路徑具有足夠的匹配特征數量，文獻[12]已經提出在一維路線中采用DTW （dynamic time warp）進行路徑匹配，精度接近1 m.本文提出的匹配算法結合了DTW 與PF，構造基于路徑的二維匹配模式，與一般的基于點匹配的模式相比，在匹配特征數量方面，具有更大的優(yōu)勢.同時通過計算地磁序列之間的相似度作為輔助定位手段.最后通過實驗對本文提出的匹配方法進行評估.

1 地磁室內定位

地磁室內定位系統(tǒng)可分為離線構圖與在線匹配兩個階段.離線構圖是利用磁傳感器遍歷匹配區(qū)域，利用收集的地磁數據采用類似“指紋”的方法建立參考圖；在線匹配是在目標運動階段實時收集所在位置的地磁數據，并利用匹配算法將其與參考圖進行最優(yōu)匹配，得出目標的最佳估計位置，整個過程如圖1.

1.1 粒子濾波（PF）算法

PF 算法是基于蒙特卡羅思想的一種最優(yōu)貝葉斯估計，在分析非線性、非高斯的動態(tài)時變系統(tǒng)問題上具有突出優(yōu)勢.一般而言，后驗概率分布p(xt|zt)十分復雜不容易獲得，當系統(tǒng)的先驗概率分布和似然函數已知時，粒子濾波器使用蒙特卡洛定位方法對其近似，原理就是利用粒子的狀態(tài)作為先驗概率，目標觀測值作為參數與粒子所在位置對應的參考值做匹配，最后推導目標的最大似然估計.整個粒子濾波算法包括三個步驟：預測，更新和重采樣.預測與更新方法如式（1）.

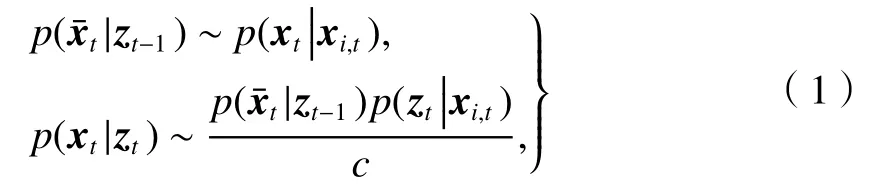
式中：xt為目標狀態(tài)；為目標預測狀態(tài)；xi,t為第i個粒子的粒子狀態(tài)；zt為觀測值；t為時間；c為歸一化常數.

為了解決迭代過程中粒子衰減問題，粒子濾波器加入重采樣（sampling importance resampling）算法.重采樣的基本思想是去除權重小的粒子，并對權重大的粒子進行復制.在二維定位中，以行人運動軌跡為粒子濾波算法的運動模型，如式（2）.

式中：l～U(0,L)；L為目標移動步幅長度；

式中：設定行人當前所在位置的方向為初始值0，θ為行進過程中與初始方向之間的偏移量.

似然函數是基于單變量高斯概率密度函數，如式（4）.

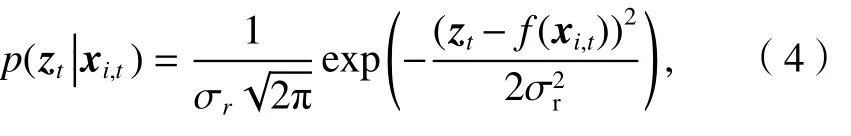
式中：σr為 觀測值zt的協(xié)方差；函數f(·)返回粒子xi,t在參考圖中對應的參考值.

式中：N為采樣粒子個數；wi,t為時刻t第i個粒子的權重.

并且，定位誤差定義為

1.2 動態(tài)時間規(guī)整算法（DTW）

在進行地磁路徑匹配（地磁序列匹配）時，收集地磁數據的行走速度不同，可能會使得由于速度不同產生的兩個序列的單個樣本不準確.用DTW 進行比較的好處是能夠允許兩個序列在時間尺度上變化.DTW 算法通過實現(xiàn)兩個序列之間的度量距離最小值，將一個序列的樣本映射到另一個序列.算法定義的距離度量具有時間尺度上的不變性.地磁路徑匹配是對室內兩條不同路徑上每個點的地磁強度進行對準，確定兩條路徑是否存在偏差，以及偏差的大小，這是室內地磁DTW 算法的概念.假設目標走過的路徑為Q，長度為K=q，某個粒子走過的路徑為P，長度為K=p.DTW 算法的度量距離定義為

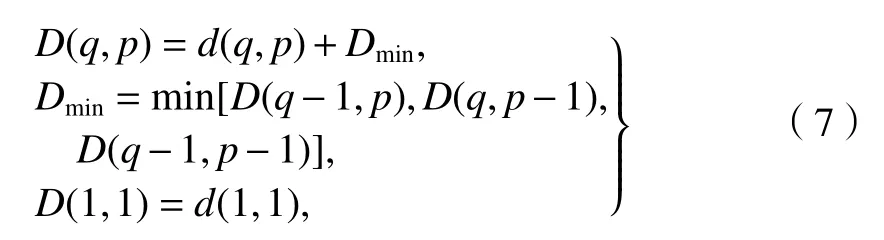
式中：D(q,p)為長度分別為q、p的路徑Q、P之間的度量距離；d(q,p)為路徑中對應點的歐幾里得距離，d(·)=‖·‖.

同時地磁序列之間的相似度可以作為輔助匹配手段，通過計算Spearman 相關系數確定相似度，該系數定義為

式中：xm、ym分別為兩條序列中第m個數據；M為序列中數據總數；、分別為兩條序列數據的平均值.

系數越高地磁序列相似度越高，并且該系數要求兩條序列的長度要一致.

聯(lián)合算法整體上還是遵循粒子濾波器的框架，整個聯(lián)合算法的流程如圖2.它與一般的粒子濾波器相比，優(yōu)勢在于：

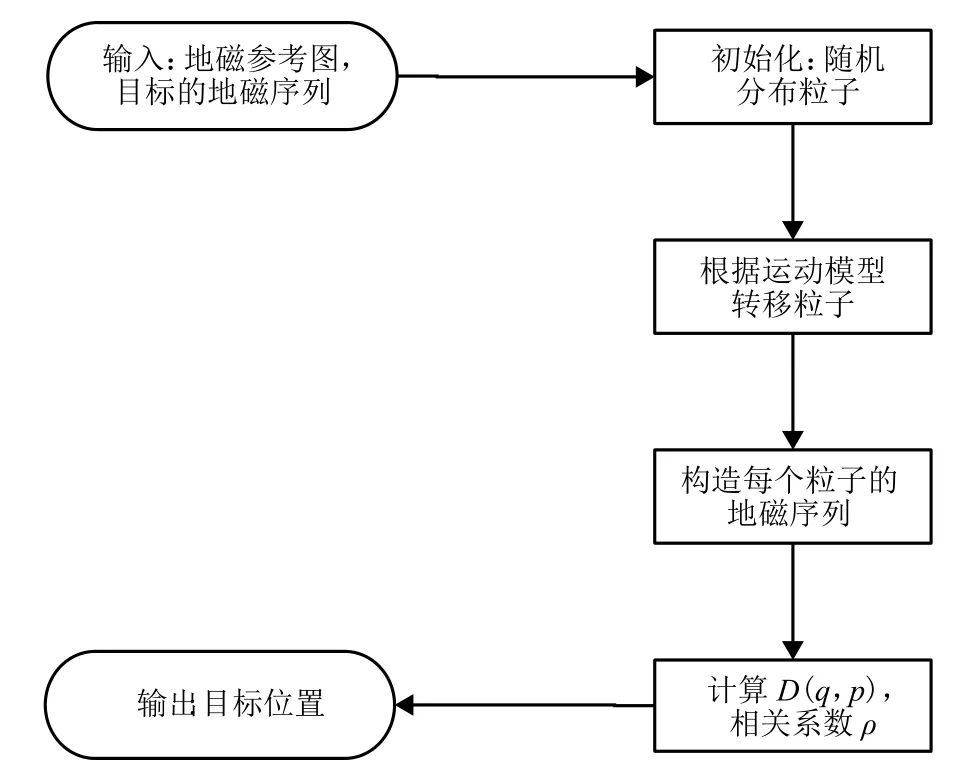
圖2 聯(lián)合算法流程Fig.2 Process flow of the joint algorithm

（1）在目標運動一定時間段后進行匹配，進而增加了匹配元素的數量，提高了匹配精度.

（2）利用DTW 算法，通過計算粒子與目標的距離度量值代替粒子權重，無需重采樣.

（3）減少了對粒子群數量的需求.

（4）利用地磁序列相似度來輔助定位.

2 實驗數據采集及參考圖構建

實驗地點是北京建筑大學測繪學院二樓走廊，長68.0 m，寬1.8 m，平面圖如圖3（a）.本文采用“指紋”模式的方法，采集二樓走廊的地磁數據用于構建參考圖（圖3（b））.

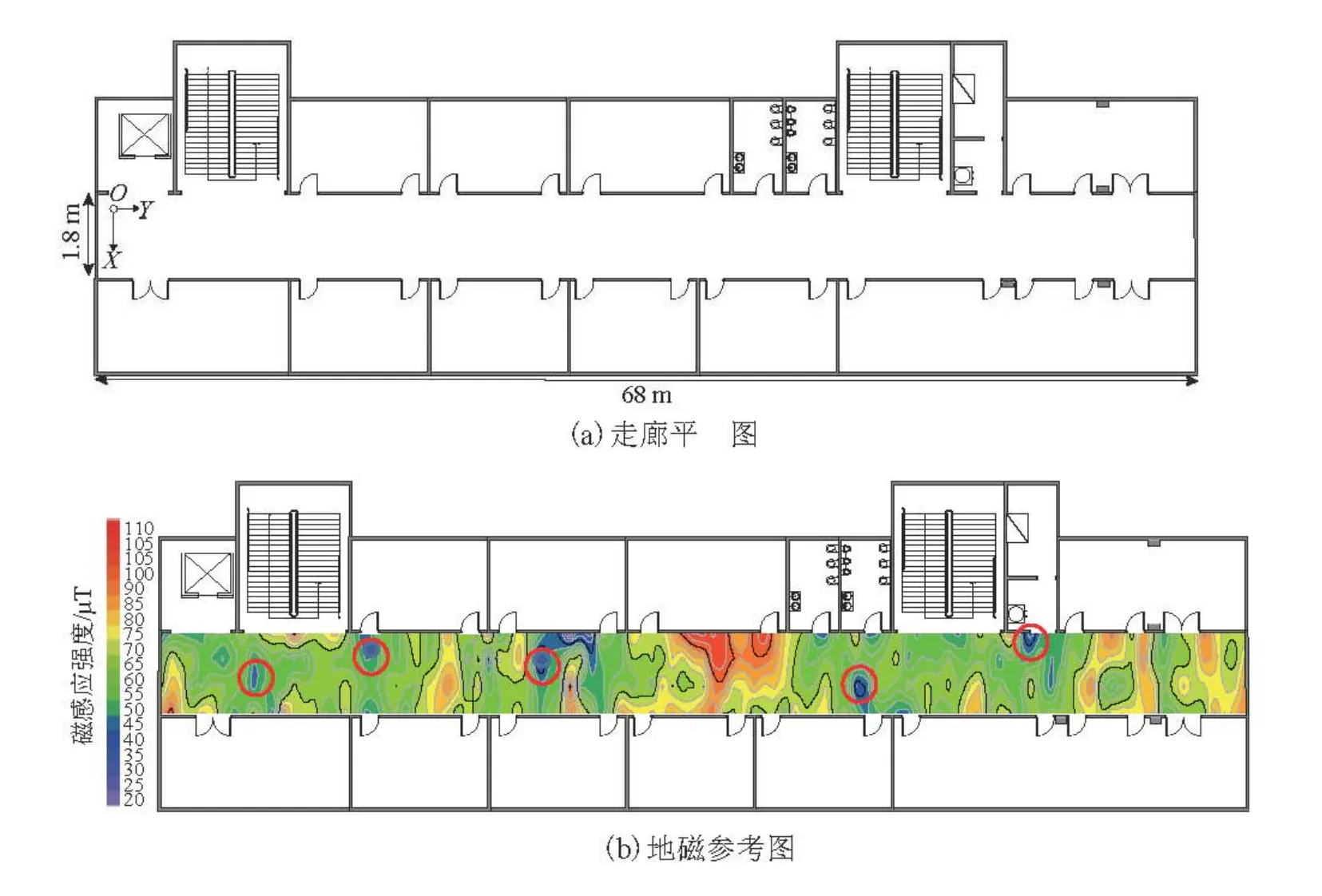
圖3 走廊平面圖以及地磁參考圖Fig.3 Corridor plan and geomagnetic reference map

為了能快速收集室內地磁數據，團隊（城市測繪研究所）開發(fā)了一款測量機器人，上面搭載的地磁傳感器HMC5983 裝載位置距離地面1.3 m，能夠避免機器人自身的影響，如圖4[13].HMC5983 體積小，具有自動偏置補償以及溫度補償功能，攜帶I2C 或者SPI 的數字接口，最大輸出功率為220 Hz，航向角的精確度為1°～2°.

實驗中，控制裝有地磁傳感器的測量機器人沿著走廊收集了4 行間隔0.6 cm 的地磁數據.機器人步長為0.2 m，每25 Hz 測量一次磁感應強度，產生三維矢量B=(Bx,By,Bz)，單位為μT，每個點采集時間10 s.為了進行定位，本文使用磁感應強度‖B‖作為匹配特征，計算方法如式（9）所示.因為磁感應強度是一個旋轉不變量，避免了設備在運動過程中輕微抖動對實驗的影響.

采集的參考地磁數據，利用克里金插值法進行處理，并且賦予網格坐標，構造的參考圖如圖3（b）.從圖3中可知，受建筑物鋼筋混凝土結構的影響，走廊地磁擾動隨空間位置的改變而發(fā)生明顯變化，因此能夠用于室內定位.而圖中紅色圓圈則表示存在地磁強度相似現(xiàn)象，這導致了室內地磁特異性的減弱，同時給定位結果帶來誤差.

圖4 測量機器人結構Fig.4 Structure of a measurement robot

3 實驗結果與分析

本文首先通過實驗分析在采樣粒子分布相同的情況下N與K對定位精度的影響.使用測量機器人隨機從某點（如點（1.2，15.4）m）開始沿著Y軸直線運動15 次，L設為0.6 m.在線采集地磁數據，獲取15 個位置點，路徑長度分為 1、2、···、14，如圖5，圖中所示相鄰兩個點位之間的路徑長度為1.另外基于路徑匹配只能從點2 開始，而且在每個位置進行匹配，所能使用的特征數量與點號的值相等.

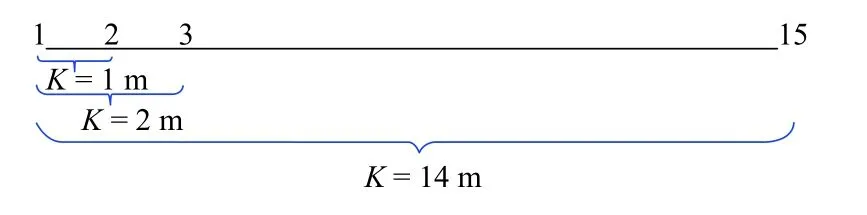
圖5 點位與路徑長度關系Fig.5 Relationship between points and path length

地磁數據采集完后，利用聯(lián)合算法將它與地磁參考圖進行匹配，其中粒子濾波算法中粒子分布的方式采用隨機分布，匹配次數設定為300 次，聯(lián)合算法通過MATLAB 計算機語言編寫實現(xiàn)，平均定位誤差與誤差占比（誤差e小于1 m）分別如圖6、7 所示.

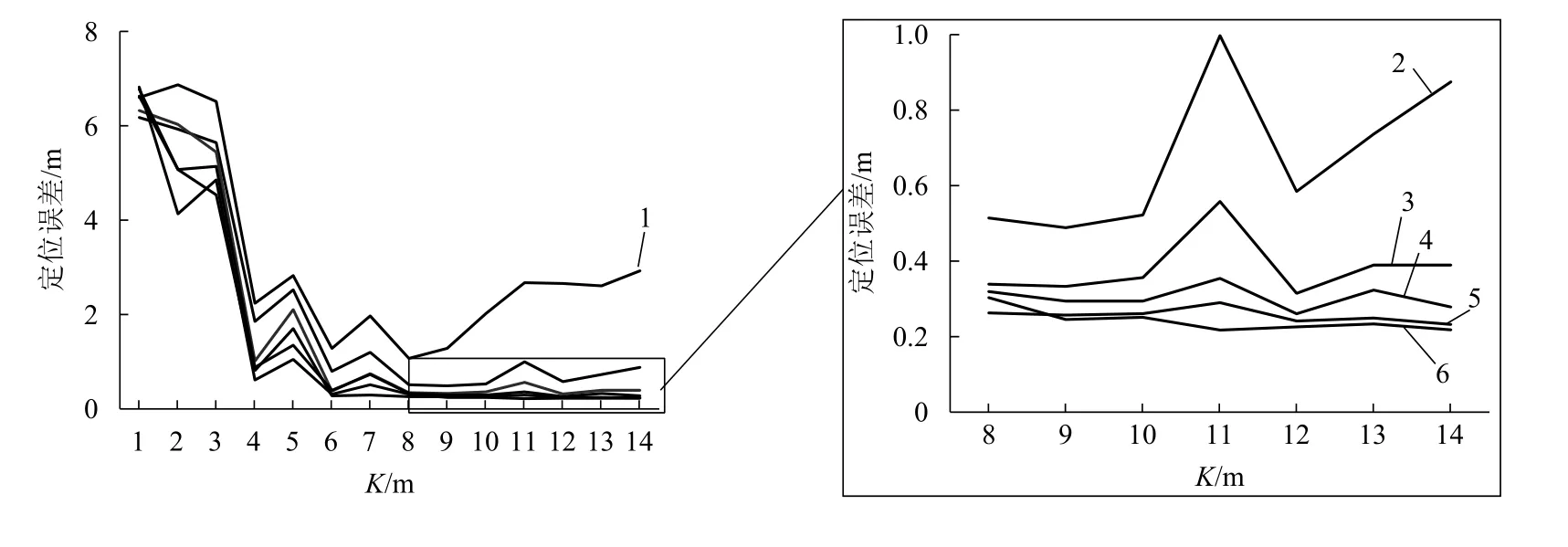
圖6 不同粒子數隨著路徑增加的定位結果Fig.6 Positioning results of different particle numbers increasing with path

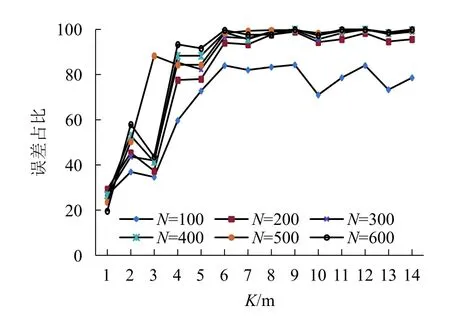
圖7 誤差占比（e ＜ 1 m）Fig.7 Proportion of error（e ＜ 1 m）

從圖6可知，當粒子稀疏時會出現(xiàn)定位不穩(wěn)定的情況，如N= 100 和N= 200，這與粒子的分布有關系.當N＜ 500 時，K= 5 m 和K= 7 m 出現(xiàn)波動情況，這與路徑的選擇有關，但不會影響實驗的整體定位結果，后續(xù)實驗會進一步說明.

充足的粒子數可以保證粒子分布密集，因此粒子隨機分布在目標周圍的概率增大，使誤差小于1 m的定位結果出現(xiàn)的概率也增大，如圖7.而且當粒子數一定，誤差小于1 m 的百分比隨著K的增加而提高；當N＞ 300 后，誤差區(qū)百分比的變化趨勢（隨著K值推移）基本保持一致.

總而言之，當N＞ 100，整體的定位精度隨著K增大而增加，尤其是當N＞ 300、K＞ 7 m 時，定位精度優(yōu)于1 m.同時表1顯示了不同粒子數對聯(lián)合算法的影響，表示粒子數與匹配時間近似成正比.并且確定后期實驗粒子數N= 400.

表1 不同粒子數匹配時間Tab.1 Time required to match different particle counts

傳統(tǒng)粒子濾波定位結果如圖8.從圖8中能看出，采用粒子濾波對同一條路徑進行單點定位的結果大致在點5 處開始收斂，但是收斂結果時好時壞，隨機匹配20 次中，最大收斂誤差能接近20 m，同樣最小收斂誤差也能小于1 m.在重復匹配300 次后，得出在第15 號點的各定位誤差范圍所占百分比情況，同時與本文提出的方法進行比較，如圖9（a）.圖中能充分說明在基于單點匹配的模式下，會導致粒子濾波器的穩(wěn)定性下降，很顯然這樣的穩(wěn)定性不足以用于室內定位，相比之下本文提出的方法具有良好的穩(wěn)定性，1 m 以內的定位精度接近100%，但是匹配時間方面，如圖9（b）所示，單點匹配所耗時間基本不變，且低于路徑匹配.

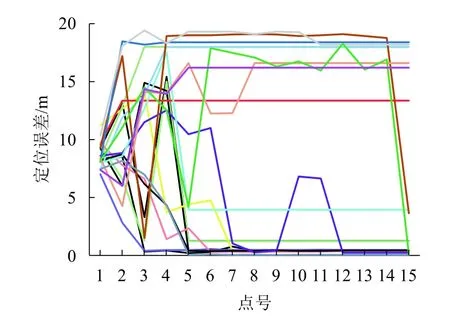
圖8 同一路徑基于粒子濾波器單點定位結果（N = 400）Fig.8 Positioning results of single point for the same path based on particle filter （N = 400）

圖9 粒子濾波器基于單點匹配和聯(lián)合算法基于路徑匹配的誤差占比以及匹配時間Fig.9 Error ratio and matching time of the particle filter based on single point matching and joint algorithm based on path matching

本文提出的方法中還加入了序列相似度作為輔助手段，實驗在計算DTW 算法后不能直接確定最優(yōu)位置估計，只能通過平均計算位置估計較好的前幾組來得出最終位置.因為DTW 算法定義的度量距離是指計算兩條序列的地磁強度差異，使得D(q,p) 值小的粒子不一定靠近目標.而加入Spearman相關系數做為相似度輔助是為了讓 ρ 與D(q,p) 進行互補.ρ 為序列間的梯度變化，當它取最大以及D(q,p) 取最小時就可以得出最優(yōu)估計位置.為了驗證輔助手段的有效性，取N= 400 分別進行匹配，結果如圖10.從圖10中可知，從K= 1 m 到K= 14 m，采用地磁序列相似度作為輔助手段都能夠提高路徑匹配過程的定位精度，路徑長度小于4 m 效果最好，路徑長度在4～8 m 之間其次.為了驗證方法的魯棒性，又隨機從不同任意點開始收集4 條路徑的地磁序列（一共5 條），移動步長不變.粒子數N設定為400，其中包括2 條直角轉彎路徑，結果如圖11.圖11中1、2、3 表示直線路徑，4、5 表示包含直角轉彎的路徑，很明顯當K＞ 9 m后，最優(yōu)定位精度在1 m 以內，而且不存在定位誤差突然劇增現(xiàn)象，說明本文所提出的算法性能可靠，具有良好的魯棒性.另外本文實驗是驗證基于路徑模式的室內地磁定位的可能性，同時得出該系統(tǒng)的定位精度，所以測量機器人的移動步長和航向角都屬于人工控制.

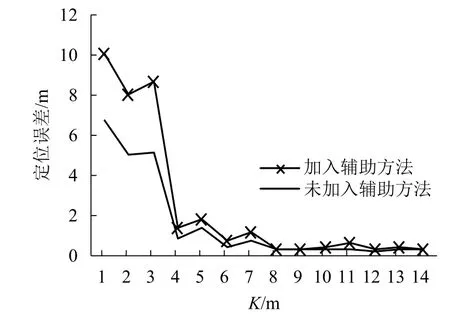
圖10 定位結果對比（N = 400）Fig.10 Comparison of positioning results （N = 400）

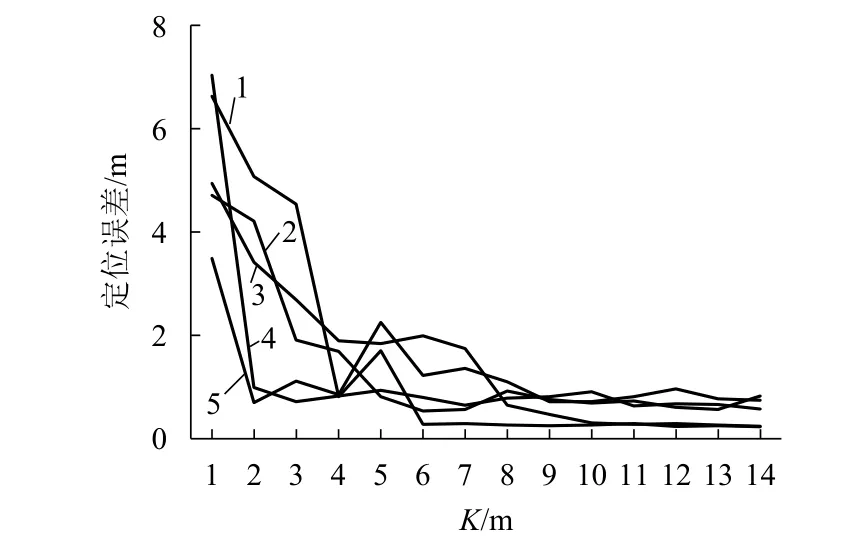
圖11 不同路徑定位誤差比較Fig.11 Comparison of positioning errors for different paths

4 結 論

在基于位置服務的發(fā)展中，室內定位是前提.各種定位方法中，基于地磁定位的方法因不需其他基礎設施投入而受到廣泛關注.然而在大型建筑中，地磁場的特異性會減弱，一般的基于粒子濾波器的定位方法會導致定位結果出現(xiàn)模糊現(xiàn)象.在本文中，提出了一種新的基于地磁的室內定位技術.該技術中有3 個創(chuàng)新點：（1）提出一種基于粒子濾波器與DTW的聯(lián)合算法；（2）一種新的基于路徑匹配的地磁定位模式；（3）使用地磁序列相似度進行輔助，后期實驗也證明了輔助手段的有效性.最后實驗證明，與傳統(tǒng)的基于粒子濾波算法的室內地磁定位方法相比，該算法有效地解決了定位模糊問題，當路徑長度和粒子數足夠時（K≥ 9 m，N≥ 400），總體定位精度優(yōu)于1 m，而且定位精度小于1 m 出現(xiàn)的概率接近100%，體現(xiàn)了該算法具有良好的穩(wěn)定性與可靠性.