鐵路貨車車體線路動態響應仿真與驗證

于躍斌 ，趙尚超 ，李向偉 ，李 強

（1.北京交通大學機械與電子控制工程學院，北京 100044；2.中車齊齊哈爾交通裝備有限公司，黑龍江 齊齊哈爾161002）

系統仿真技術已經成為高技術產業不可缺少的分析、研究、設計、評價、決策等的重要手段，近年來在軌道交通領域也得到廣泛應用[1].鐵路貨車提速、重載后，尤其輕量化技術已被普遍采用，車體在線路運行時的動態響應是工程人員所關注的一項重點，而車體僅僅是鐵路列車大系統的一個子系統，受線路、輪軌接觸、轉向架懸掛、車鉤緩沖、裝載及結構本身等因素的影響，其在線路運行過程中的動態響應較為復雜，如果按大系統仿真分析方法對車體結構受到的響應進行分析，建模時考慮需要考慮的因素會很復雜，對其結果的評估也會出現較大偏差.并且我國鐵路貨車領域仿真的輸入多采用美國機務標準手冊中的載荷譜[3].近年來，雖開展了我國鐵路線路測試，將測試結果統計為簡單工況譜作為仿真的輸入[4]，由于不考慮時間效應，這種仿真結果沒辦法與線路測試時域結果進行對比分析.為此本文將以車體為研究對象，通過采集車體在實際線路運行過程中的加速度及動應力響應，并以此為迭代目標輔助于模擬臺架的試驗數據，作為仿真建模的已知參數建立與試驗對應的多體仿真模型，以實現鐵路貨車車體線路動態響應的仿真方法.

1 仿真原理

1.1 線路動態響應的臺架模擬實驗

基于線路實際測試數據及車體在臺架試驗的線路動態響應模擬，可以簡化邊界條件，為車體子系統的仿真建模提供已知輸入.臺架模擬試驗主要由電液系統、機械系統、電氣系統、測試采集及處理系統等組成，以垂向、橫向、縱向及車鉤作動器為加載系統，通過加載機構的動作，模擬車體在線路上的運行工況，通過實測線路目標信號的迭代，使車體在臺架上與在線路上的動態響應基本一致[2-4]，如圖1所示.

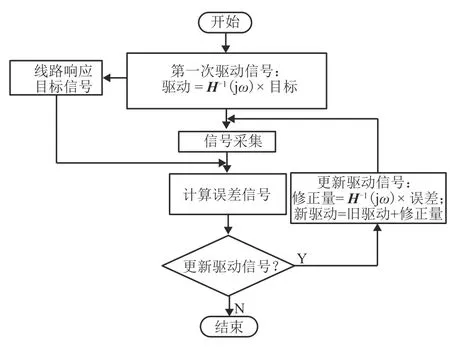
圖1 線路動態響應目標信號的迭代流程Fig.1 Iterative flowchart of dynamic response target signal

根據圖1，具體的迭代過程是把被試對象放置于試驗臺架上，對試驗臺架及被試車體所組成的系統進行系統辨識，獲得響應與激振輸入之間的頻響關系，建立傳遞函數矩陣H(jω)，進而得到系統的阻抗矩陣H-1(jω).

求第一次迭代的控制信號x1(t)，

式中：fIFFT(·)為 傅里葉逆變換；Ys(jω)為目標函數ys(t)的傅里葉變換.

將11 個通道信號作用于各激振點，在車體上得到響應信號y1(t)，誤差時間歷程為

當誤差計算精度大于某一預先設定的規定值，則進行補償運算，得到新的激勵x2(t)，

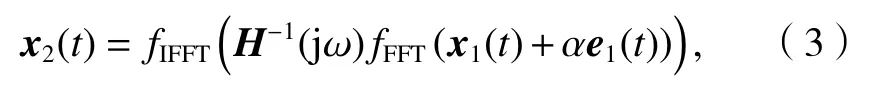
式中：α為加權系數，取誤差的百分數進行新激勵計算；fFFT(·)為傅里葉變換.

用x2(t) 進行激振，得到響應y2(t).若根據誤差進行第3 次迭代，則求再現響應信號所需的驅動信號x3(t).這樣，對于第i次迭代有

當誤差信號足夠小時，可結束迭代，并獲得驅動文件，在該信號激振下，即可在被試車體上再現線路的動態響應.

1.2 仿真模型的理論基礎

仿真建模是基于剛柔耦合多體動力學原理[5]，首先建立與試驗臺對應的剛體模型，然后與建立的柔性車體進行裝配，將上述驅動文件作為仿真的輸入，完成車體在線路動態響應的仿真分析.

模型中第l（l= 1 ,2,···）個剛體的廣義坐標通過3 個平動坐標x、y、z和3 個轉動坐標ψ 、θ 、φ 寫成6 ×1 矢量列陣，如式（5）.

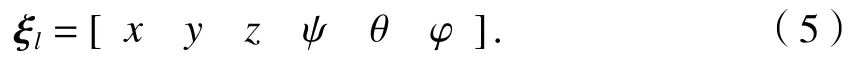
剛體系統帶拉格朗日乘子的能量方程為

式中：T為廣義坐標下的動能；Ql為廣義坐標下的方向力；n為約束方程的個數；λj為拉格朗日乘子；R為約束的表達.

鐵路貨車將車體作為柔性體時，在剛體的廣義坐標中添加模態坐標qm后變成柔性體的廣義坐標，如式（7）.

式中：m=1,2,···,M，M為柔性體的模態階數.

為了能夠獲得較好的擬合靜態、動態載荷條件下結構變形所需的模態，采用Craig-Bampton 模態綜合法來獲取所需要的模態集 Φ.故剛柔耦合系統帶拉格朗日乘子的方程為

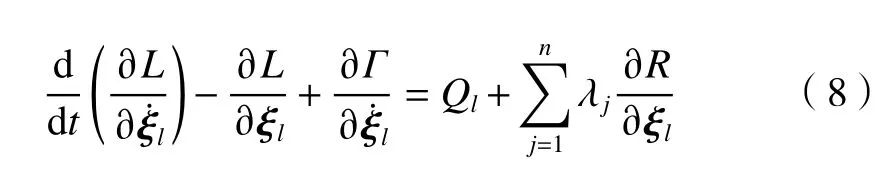
式中：L為動能與勢能的差；Γ為系統損耗函數.

對振動方程進行求解可獲得彈性體廣義模態坐標向量的時間歷程，根據模態坐標，疊加模態應力以獲得動應力的時間歷程.

2 仿真模型的建立

仿真分析模型包含臺架加載模型及車體模型兩部分，其中將臺架模型的模擬搖枕、作動器及連接桿考慮為剛體，將車體作為柔性體.

2.1 多剛體加載臺架模型

試驗臺加載系統主要由模擬搖枕結構、電液伺服控制系統、空氣彈簧系統3 部分組成.試驗臺對車體加載控制過程為：驅動信號通過伺服控制系統向作動器伺服閥發送驅動指令，通過作動器作用到模擬搖枕上，模擬搖枕通過心盤及旁承傳遞給車體，實現對車體的控制，車體產生的動態響應再由測試系統采回與目標進行對比.系統傳遞和加載控制如圖2和圖3所示.

電液伺服控制系統的油缸力、位移反饋信號為最終施加給系統機械結構的載荷，仿真可僅建立機械系統模型，并將此反饋信號作為輸入.

完成了機械模型裝配、設置參數和約束關系，模型包含了189 個移動部件，1 個圓柱副，32 個球鉸，10 個滑移副，155 個固定約束，8 個點線約束和12 個位移驅動，自由度數為26，如圖4所示.

圖2 系統傳遞結構示意Fig.2 Schematic diagram of system load transfer structure

圖3 加載系統簡化框圖Fig.3 Simplified block diagram of loading system

圖4 試驗臺架仿真模型Fig.4 Simulation model of test rig

2.2 柔性車體模型的建立

以某礦石敞車車體為例，采用shell 單元模擬，單元長度為30 mm，如圖5.傳統方法一般不建立焊縫等細部結構，這樣做將增大連接部位的剛度，特別對側墻橫向振型影響較大，而本文在建立柔性車體時，采用焊縫作為連接單元，經對比發現模態數據與試驗數據更為接近[6].

所裝載貨物對重車的動態響應影響較大，而對于貨物的建模方法，目前研究較少，且研究成果多集中在散粒貨物對車體側墻和端墻的影響[7-8].為研究貨物對車體動態響應的影響，利用試驗臺對不同散粒狀態進行了模態試驗，結果表明，散粒的實、松狀態對車體剛體和彈性體頻率影響很小[9]，鑒于此，為簡化模型，這里將散體采用質量單元附加到底架地板單元上.

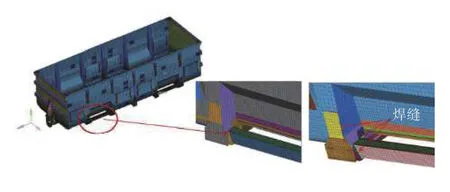
圖5 建立帶焊縫的車體模型Fig.5 Building the wagon body with welds

車體不同的模態振型對應的模態阻尼值通過模態試驗的線性插值獲得，超出的部分按折中5%選取.本文柔性體采用改進的Craig-Bampton 模態計算，根據線路加速度的頻譜分析結果，將主模態設置為20 階，主模態截止頻率為10.6 Hz，約束模態取66 階.

2.3 多剛體臺架模型與柔性車體模型連接

剛性體與柔性體處理難點為心盤和旁承存在高非線性問題，傳統采用摩擦力矩接觸模型[10-11]，而試驗臺為增大心盤連接處的阻尼，將心盤連接處的磨耗盤取消，保持車體上心盤尺寸不變，對下心盤進行了重新設計，將間隙減小，由原來單邊間隙2.5 mm減小到1.0 mm，增大了系統的線性傳遞.故建模時將心盤模型簡化為4 個較大剛度的單邊彈簧，常接觸旁承簡化為小阻尼的變剛度彈簧，如圖6所示.

完成裝配后進行了模態分析，如表1所示.表1的對比結果表明達到了仿真預期，仿真值略高的原因是由于該車體較短，剛性較大，仿真模型與實際結構稍有差異.

圖6 心盤簡化模型Fig.6 Simplified model of the centre plate

表1 模態頻率結果對比Tab.1 Results comparison of modal frequency Hz

3 線路動態響應仿真的輸入

將與控制信號對應的油缸力、位移反饋信號作為仿真輸入，這樣處理的優點是考慮液壓系統和控制系統引起的相位滯后.由于試驗臺是自下而上的激勵模式，若作動器全部采用位移控制模式時，由于系統的強耦合特性，仿真結果不易收斂.對于鐵路貨車車體無約束的仿真模式，仿真采用力控制和位移控制的組合是比較恰當的[2]，力控為車鉤力，其余作動器為位控，如圖7所示.

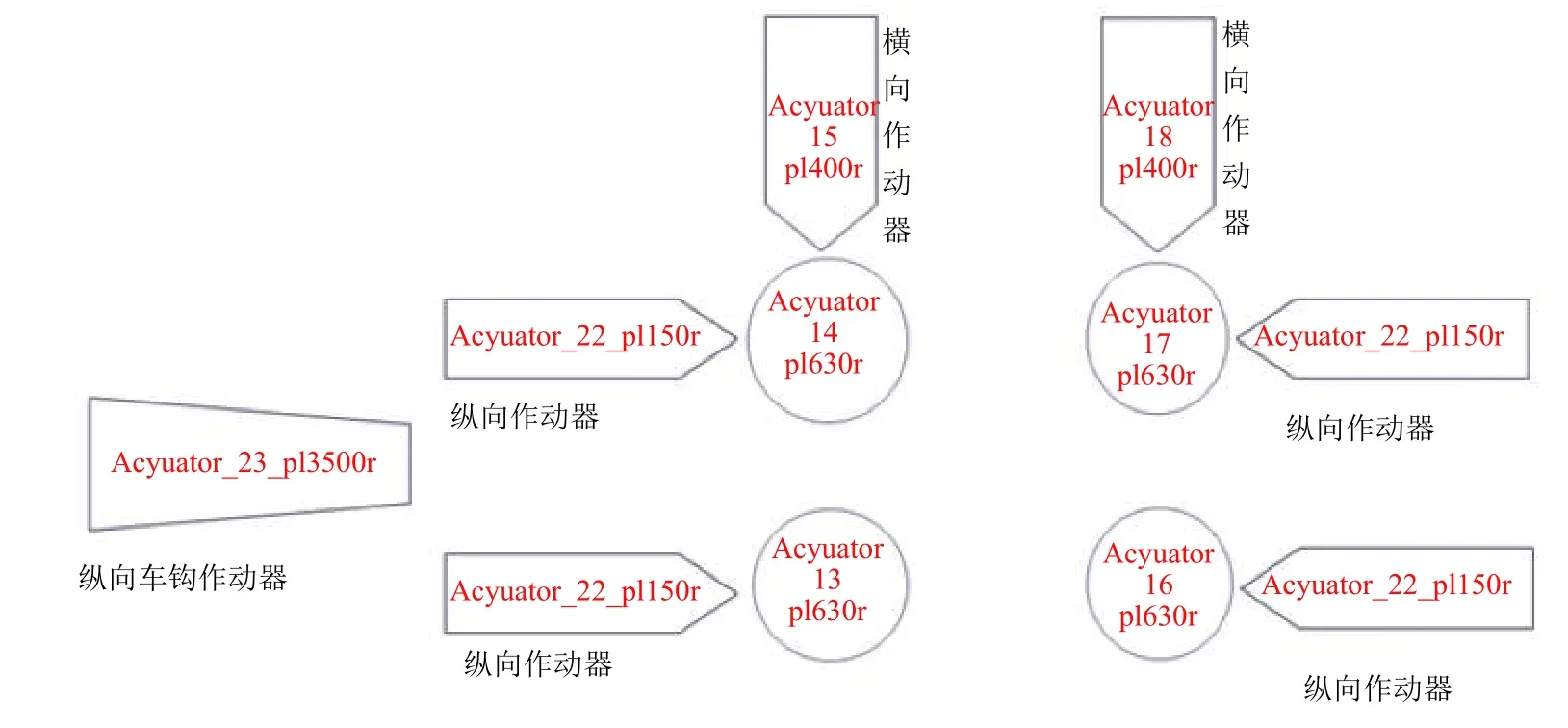
圖7 作動器分布圖Fig.7 Disposition of actuators

4 線路動態響應仿真與試驗驗證

選取試驗臺迭代好的驅動文件（縱向車鉤力及垂、橫作動器驅動文件），同時施加到仿真模型上和試驗臺架上，對比系統響應，結果見圖8～11 所示：搖枕垂向及橫向加速度響應結果模擬較好，仿真與試驗RMS （root mean square）誤差最大值為9.00%，但仿真與試驗車體RMS 誤差接近30.00%，經分析是由于重車模型散粒簡化及非線性心盤、旁承建模影響，導致了傳遞到車體的振動加速度有一定差異，仿真結果比試驗結果幅值偏低，尤其在低頻部分誤差較大.

圖8 搖枕垂向加速度對比Fig.8 Comparison of vertical acceleration of bolster

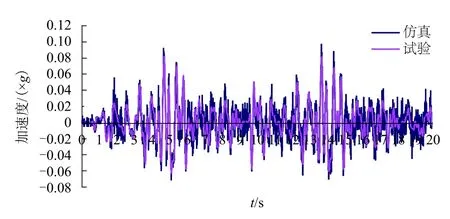
圖9 搖枕橫向加速度對比Fig.9 Comparison of lateral acceleration of bolster

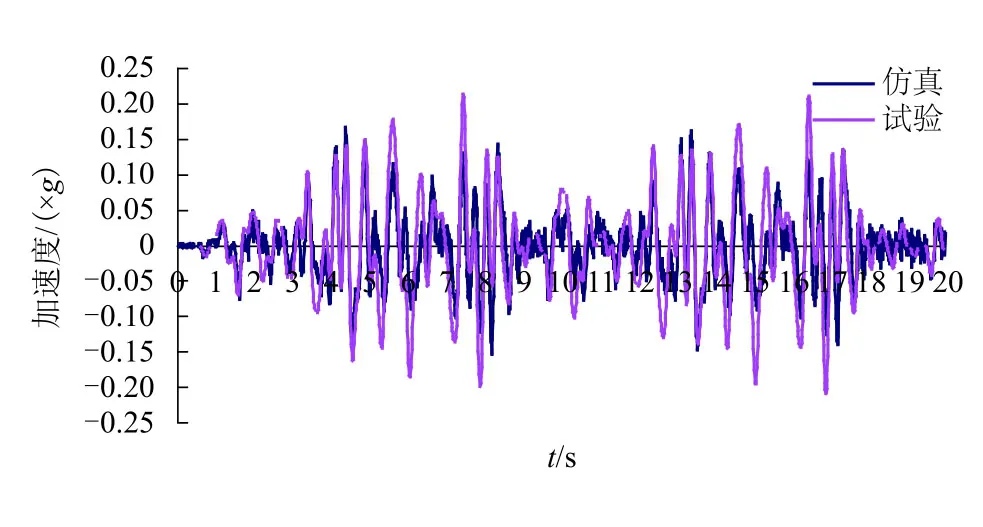
圖10 車體枕梁垂向加速度對比Fig.10 Comparison of vertical acceleration of body bolster

進一步對車體垂、橫向振動加速度進行PSD（power spectrum density）分析，如圖12：誤差較大的頻率段為1.0～2.0 Hz，為表1中的側滾振型控制區；進一步考慮到仿真步長選擇引起的高頻沖擊，故僅保留時域1.5～15.0 Hz頻率的主要成分，濾波后的計算結果如圖13、14 所示.統計分析結果見表2，車體枕梁垂、橫向振動加速度的試驗結果和仿真結果對應較好，兩者的RMS 誤差低于8.57%.

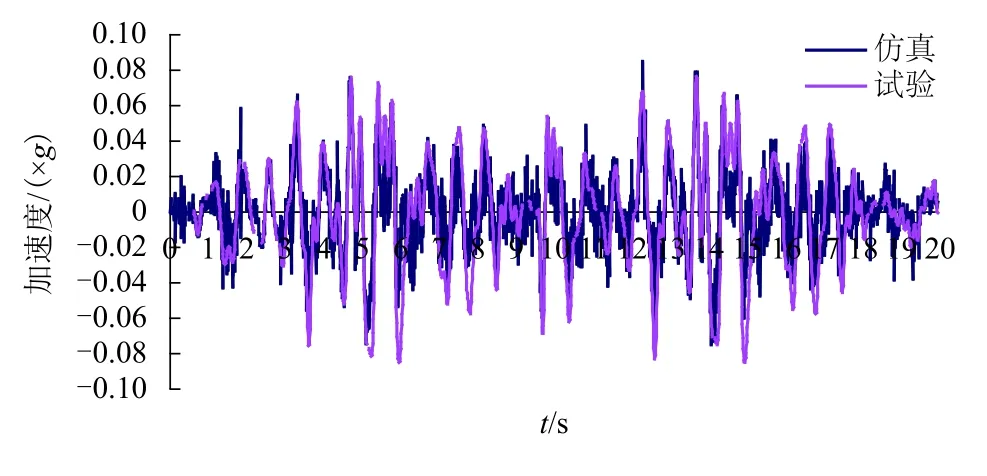
圖11 車體枕梁橫向加速度對比Fig.11 Comparison of lateral acceleration of body bolster

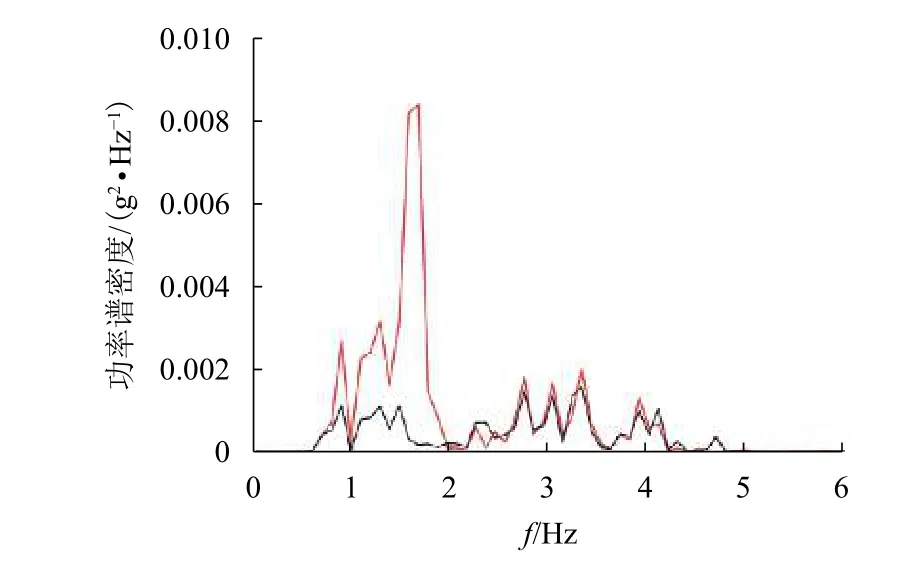
圖12 模擬搖枕振動加速度響應的PSD 分析結果Fig.12 PSD analysis results of acceleration response of dummy bolster

圖13 車體枕梁垂向加速度對比的仿真結果Fig.13 Comparison of vertical acceleration of body bolster with the simulation results

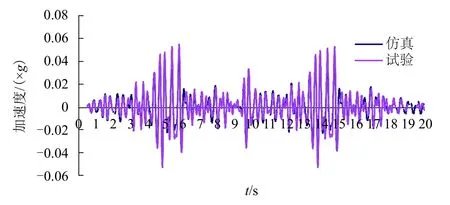
圖14 車體枕梁橫向加速度對比的仿真結果Fig.14 Comparison of lateral acceleration of body bolster with the simulation results

表2 車體枕梁振動加速度的統計結果Tab.2 Statistical results of acceleration of body bolster

圖15對比了車體大橫梁和中梁焊縫動應力時域波形.從圖15中可知，仿真結果在3 s 后進入穩態振動階段，試驗和仿真結果的波形基本一致，幅值略有差異，原因主要是有限元建立時的網格尺寸的影響.

圖15 仿真與試驗動應力對比Fig.15 Stress comparison between simulation and test

5 結 論

抽取車體子系統為研究對象，通過采集車體在實際線路運行過程中的加速度及動應力響應，并以此為迭代目標，輔助于模擬臺架的試驗數據，作為仿真建模的已知參數，建立了26 個自由度的與線路模擬試驗臺架對應的仿真模型，建模時還考慮了散粒貨物、車體模態及焊縫連接剛度對仿真結果的影響，實現了車體線路動態響應的建模與仿真.

通過在仿真分析中引入試驗臺架模型，能夠解決試驗與仿真邊界差異性，實現仿真與試驗的交流機制，使仿真與試驗相互指導、相互補充.

仿真與試驗結果表明：搖枕垂向及橫向加速度響應結果模擬較好，仿真與試驗RMS 誤差最大值為9.00%；在1.5～15.0 Hz 主要頻率段，車體枕梁垂、橫向振動加速度的試驗結果和仿真結果的RMS 誤差低于8.57%，車體關鍵焊縫仿真與試驗的動應力響應波形基本一致；通過與試驗結果的對比驗證，該車體子系統的仿真結果基本反映了車體在實際線路運行時的動態響應情況.