空間引力波探測任務的入軌誤差分析

李 卓，王有亮，鄭建華，李明濤*

(1.中國科學院 國家空間科學中心，北京 100190；2.中國科學院大學，北京 100039)

1 引 言

2016年，美國地基激光干涉引力波天文臺(LIGO)第一次完成地面引力波信號探測，檢驗了廣義相對論的正確性，也預示人類可以通過引力波探測來認識宇宙結構和天體的演化。為了擴展引力波探測頻段，對0.01 mHz～1 Hz左右中低頻引力波進行探測，需要開展空間引力波探測活動。空間引力波探測任務具有更寬廣的視野和大量的波源，涉及的關鍵技術包括無拖曳控制，高精度激光測距，微推進技術，大尺度高穩定編隊構型設計等[1]。

20世紀90年代開始美國國家航空航天局(NASA)和歐洲航天局(ESA)共同提出了空間激光干涉引力波探測項目LISA(Laser Interferometer Space Antenna)，旨在觀測由超大質量黑洞合并和由中子星或黑洞組成的雙星系統所產生的引力波[2]。LISA任務包括3個航天器，在地球軌道后方20°左右位置共同構成臂長為2.5×106的等邊三角形。利用空間自由懸浮測試質量塊作為傳感器，將引力波信號轉化為測試質量塊間距變化的信號，也是干涉儀臂長的變化[3]。

中國科學家也提出了類似的引力波探測項目，其中包括太極計劃和天琴計劃。太極計劃由位于等邊三角形頂端的三顆衛星組成，旨在探測中低頻波段的引力波。太極計劃的主要科學目標是觀測雙黑洞并合和極大質量比天體并合時產生的引力波輻射，以及其它的宇宙引力波輻射過程[1]。中山大學也提出了天琴計劃，天琴計劃在距地球105km的近圓軌道內放置三顆航天器形成等邊三角形，來驗證引力波在中低頻的存在和地球重力測量等其他觀測內容[4-5]。

空間引力波探測通常會維持四年以上任務周期，由于初始入軌誤差等不確定擾動的存在，使構型發生變化，可能導致其不再滿足任務要求。因此需要對誤差傳播進行分析。已知常用的方法有Monte-Carlo法，通過抽樣實驗統計狀態量的均值和標準差。Monte-Carlo法原理簡單，對各種誤差普遍適用，然而為得到準確值需要進行多次抽樣，當任務周期長時，計算量大，耗時長。

對于非線性誤差傳播分析問題，可以運用協方差分析方法，混沌多項式展開法，狀態轉移張量法，微分代數方程法，高斯混合模型法，解Fokker-Plank 方程等方法解決[6]，工程實際中非線性誤差通常符合正態分布形式，需要根據實際情況選擇合適的方法。線性協方差方法多用于分析動力學模型為線性函數的軌道預報、交會、轉移等問題，可快速獲得誤差傳播結果[7]。已有的研究結果可以解決線性模型下的空間引力波探測誤差傳播問題[8]，對于非線性模型，可用協方差分析描述函數法(CADET)解決。CADET法對非線性函數進行統計線性化，然后通過積分計算狀態變量的均值和協方差矩陣。不同于Monte-Carlo法的耗時長和線性協方差法的精度低，CADET方法計算速度快且精度高，適用于空間引力波探測軌道誤差分析問題。

本文運用CADET方法分析了空間引力波探測任務構型在入軌誤差下的穩定性，并研究了位置誤差和速度誤差的大小和方向對構型穩定性的影響。

2 空間引力波探測任務動力學模型

選取J2000日心慣性坐標系作為參考坐標系，航天器受到太陽引力及其他天體的攝動力。衛星在空間運動中主要受太陽引力及水星、金星、地球、火星、木星、土星、天王星、海王星和冥王星的攝動力作用。以LISA為例，對于相同初始條件，考慮以上所有力的作用時，其臂長變化約為2.9×105km，當去掉金星、地球、木星的作用時，臂長變化分別變為2.4×105km，2.0×105km，2.7×105km；而去掉其他天體作用時臂長變化仍然保持在2.9×105km左右。因此為簡化模型，只考慮金星、地球、木星的攝動力[8]。空間引力波探測任務動力學模型表示為[9]:

(1)

其中，Rk表示三顆衛星的位置矢量，k=1,2,3。Ri表示金星、地球和木星的位置矢量，i=1,2,3。μ0表示太陽引力常數，μi分別表示金星、地球和木星的引力常數，i=1,2,3。

定義Rij(t)=Rj(t)-Ri(t),(ij=12,23,31)為衛星之間的相對位置矢量。衛星編隊動力學指標分別為臂長L，呼吸角θ，臂長變化率V，星地距離D，可用公式(2)～(5)表達。

Lij(t)=‖Rij(t)‖ ,

(2)

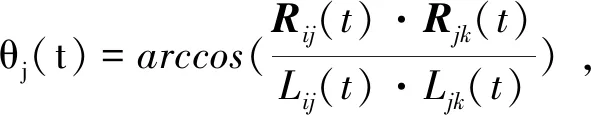
(3)

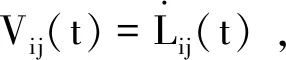
(4)

D(t)=‖Re(t)-Rc(t)‖ ,

(5)

其中：Re是地球位置矢量，Rc是三衛星中心位置矢量。

3 CADET在空間引力波探測任務軌道誤差分析中的應用

若x(t)是系統狀態向量；F(t)是系統狀態矩陣，無過程擾動的線性連續隨機系統微分方程是:

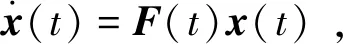
(6)

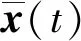
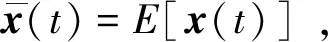
(7)

p(t)=E[δx(t)δxT(t)] ,

(8)

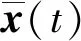
(9)

根據第二節，本文的動力學模型是非線性系統，可以表示為：

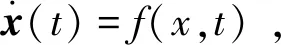
(10)

其中，x(t)是方程的狀態變量，x1～x18為衛星1,2,3的位置速度；x19～x21為臂長，x22～x24為呼吸角，x25～x27為臂長變化率；x28為星地距離。運用CADET方法分析入軌誤差對空間引力波探測任務的影響，需對系統進行統計線性化。

(11)

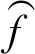
(12)

式(12)的計算比較復雜，工程中常常用如下方法簡化：

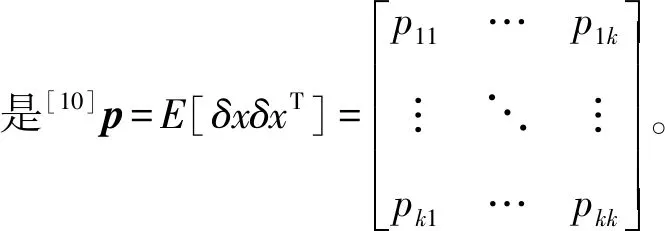
已知f(x)關于x一階可微，在m進行f(x)的一階泰勒展開，得

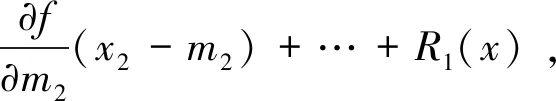
(13)

忽略一階泰勒余項R1(x)，求式(13)期望值，f(x)的線性化形式是

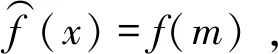
(14)

動力學方程的描述函數N為[12]

(15)

其中，I為28×28的單位矩陣，n為

(16)

式中，f1至f28包括下列方程：f1至f18為衛星1，2，3的位置速度；f19至f21為臂長L12，L13，L23；f22至f24為呼吸角θ1，θ2，θ3；f25至f27為臂長變化率V12，V13，V23；f28為星地距離D。

n的具體形式是

(17)

其中，

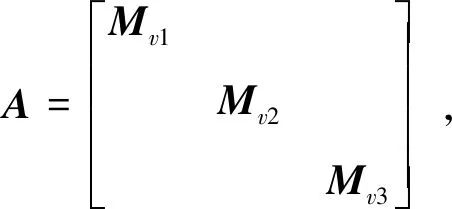
(18)

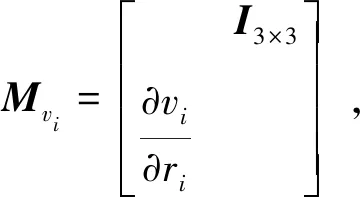
(19)

i(i=1,2,3)的速度對位置的偏導。

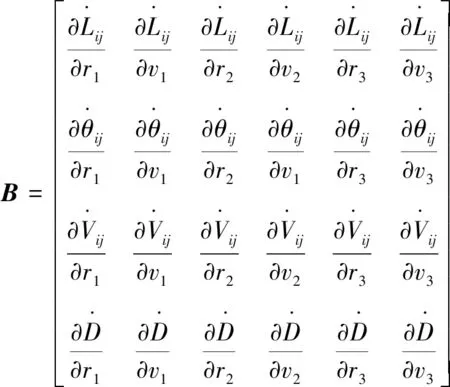
(20)

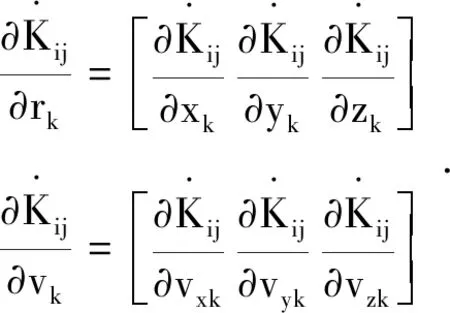
(21)

其中:K包括臂長L、呼吸角θ、臂長變化率V和星地距離D，其中ij=12,13,23，k=1,2,3。

根據CADET方法知，具有初始誤差，空間引力波探測任務航天器在J2000日心慣性坐標系中的狀態均值與協方差的微分方程如下[11]:

(22)

其中，初始條件m0包括三衛星初始位置速度和臂長、呼吸角、臂長變化率和星地距離，p0為對角線矩陣，數值由三衛星初始位置和速度誤差決定，N(t)由式(15)～(21)求出。根據以上條件，可通過積分求出任意時刻的均值和協方差矩陣。

4 CADET仿真驗證

基于動力學模型，以任務周期內一直滿足指標要求為標準選擇合適的位置速度初始條件，并加入正態分布誤差。分別用CADET法和Monte-Carlo法求任務周期10年內構型的臂長，呼吸角，臂長變化率和星地距離的均值和標準差。

圖1給出了CADET法和Monte-Carlo法求出的均值和標準差隨時間變化的結果。其中圓圈為Monte-Carlo法抽樣仿真1 000次結果，實線為CADET法結果。由圖1可知，兩種方法結果一致，以Monte-Carlo法的仿真結果作為標準，可以認為CADET法是有效的。

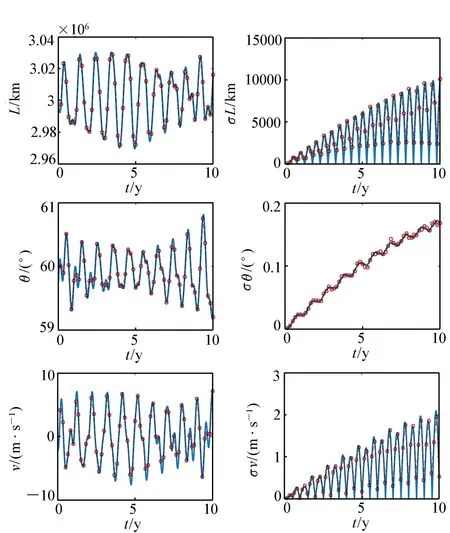
圖1 CADET法和Monte-Carlo法的對照結果Fig.1 Comparison diagrams of CADET and Monte-Carlo

任務過程中將產生大量數據，所以選取一個特殊點(10年周期內的最后時刻的數據)進行分析。考慮初始誤差時CADET法和Monte-Carlo法均值、標準差誤差和相對誤差如表1所示。

由表1可知，臂長均值相對誤差不超過0.017 8%，標準差相對誤差不超過5.600 4%；呼吸角均值相對誤差不超過0.014 5%，標準差相對誤差不超過4.780 2%；臂長變化率均值相對誤差不超過1.633 6%，標準差相對誤差不超過5.339 7%；星地距離均值相對誤差不超過0.028 8%，標準差相對誤差不超過2.833 7%。說明CADET方法對于空間引力波探測誤差分析問題確實準確有效。

表1 CADET法和Monte-Carlo法結果比較Tab.1 Results comparison of CADET and Monte-Carlo methods

5 基于CADET的空間引力波探測軌道誤差傳播分析

在空間引力波探測任務過程中，航天器面臨的入軌誤差是不確定的，不同的入軌誤差會對構型產生不同程度的影響。當使用Monte-Carlo法分析入軌誤差對構型影響的不確定性時，需要多次抽樣保證結果的可靠性，因此解決問題的過程將花費大量時間。現在已知CADET方法對于空間引力波探測誤差分析問題準確有效，可以運用CADET方法進行誤差傳播分析。

航天器的入軌誤差主要分為位置誤差和速度誤差，下面將對這兩類誤差對構型指標產生的影響進行分析。以空間引力波探測任務為例，臂長要求為3×106km，呼吸角變化小于1°，臂長變化率小于10 m/s，星地距離小于6.5×107km時可認為構型滿足空間引力波探測任務要求。初始 構型如圖2所示，1、2、3曲線分別代表衛星1、2，衛星1、3，衛星2、3之間的指標變化情況，其中臂長最大值為3.014×106km，呼吸角最大值為60.37°，臂長變化率最大值為3.325 m/s，標準差均為0。

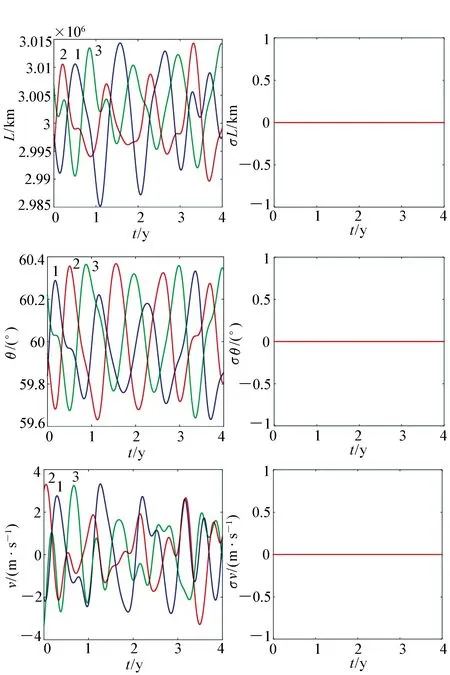
圖2 初始構型Fig.2 Initial constellations

5.1 誤差方向對構型的影響

(1)不同方向的位置誤差

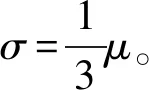
當同時向3顆衛星增加大小相等的位置誤差時，誤差的方向對構型產生顯著影響。徑向誤差使構型標準差產生的變化遠大于其他兩個方向的誤差。徑向位置誤差增加了衛星的勢能，所以構型產生的擾動更大。因此，航天器發射時需優先考慮減小徑向位置誤差。

(2)不同方向的速度誤差

同時向衛星1,2,3增加均值為1 cm/s，方向分別沿徑向，切向和法向的正態分布的速度誤差，構型變化如表3所示。

當同時向3顆衛星增加大小相等的速度誤差

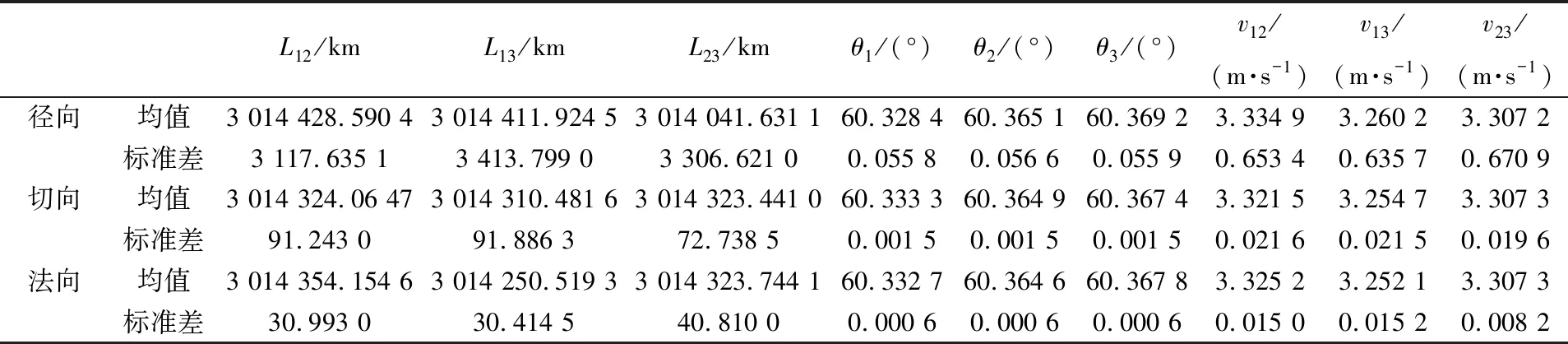
表2 位置誤差方向對構型的影響Tab.2 Effect of position error direction on constellation

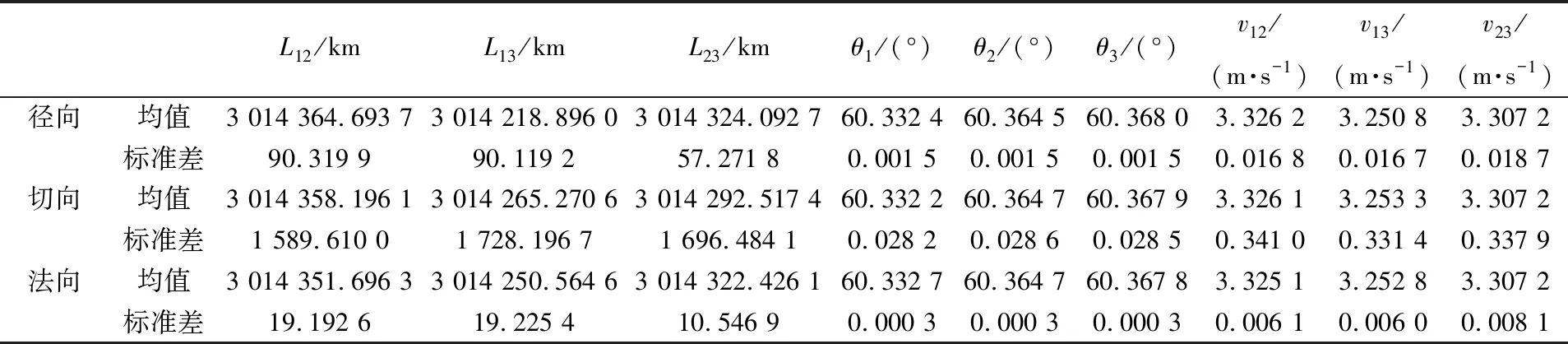
表3 速度誤差方向對構型的影響Tab.3 Effect of velocity error direction on constellation

時，誤差的方向對構型產生顯著影響。切向誤差使構型標準差產生的變化遠大于其他兩個方向的誤差。切向速度誤差增加了衛星的動能，所以構型產生的擾動更大。因此，航天器發射時需優先考慮減小切向速度誤差。

5.2 誤差大小對構型的影響

(1)不同大小的位置誤差

因為徑向位置誤差對構型影響最大，因此在本節中僅以徑向位置誤差為例分析誤差大小對構型的影響。

首先以任務周期4年為例，同時向衛星1,2,3增加正態分布的徑向位置誤差，誤差均值分別為100 km，1 000 km，構型變化表4所示。

同時向三顆衛星增加徑向位置誤差時，位置誤差對構型的影響不明顯。當誤差均值為100 km和1 000 km時，只考慮均值時構型指標滿足要求，但觀察標準差發現，1 000 km時標準差增大，構型發散不滿足指標要求。

表4 誤差大小對構型的影響(周期4年)Tab.4 Effect of error magnitude on constellation(T=4 years)

(2)不同大小的速度誤差

因為切向速度誤差對構型影響最大，因此在本節中僅以切向速度誤差為例分析誤差大小對構型的影響。

同時向衛星1,2,3增加正態分布的切向速度誤差，誤差均值分別為1 cm/s，10 cm/s，構型變化如表4所示。

向三顆衛星同時增加相同方向速度誤差時，速度誤差對構型的影響不明顯。當誤差均值為1 cm/s和10 cm/s時，只考慮均值時構型指標滿足要求，當誤差均值為10 cm/s時雖然標準差增大，但由于任務周期短，構型發散程度小，仍然滿足指標要求。

為比較周期4年和10年時誤差大小對構型的影響，對周期為10年的情況重復上述仿真，結果如表5所示。當位置誤差為100 km和速度誤差為1 cm/s時構型滿足指標要求；當位置誤差為1 000 km和速度誤差為10 cm/s時構型不滿足指標要求。當比較任務周期為4年和10年兩種情況，發現標準差大小隨時間增加，任務周期延長時，大小相等的入軌誤差會使構型產生更大擾動。

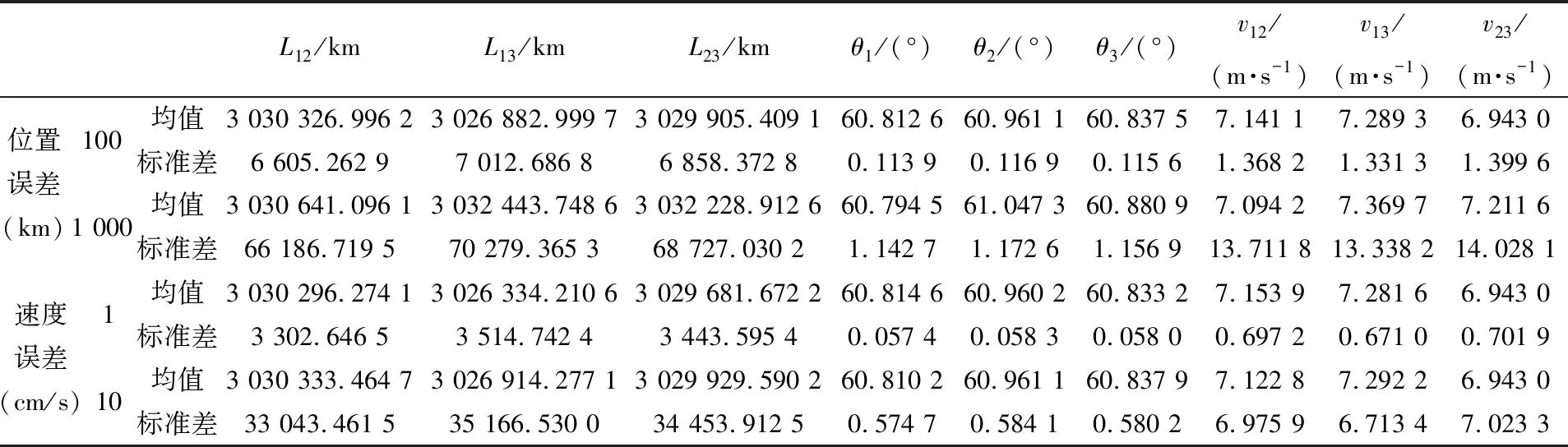
表5 誤差大小對構型的影響(周期10年)Tab.5 Effect of error magnitude on constellation(T=10 years)

5.3 三星間相對誤差方向對構型的影響

當航天器發射存在入軌誤差時，三衛星誤差的相對方向可能會對構型產生不同的影響。下文將探究相對方向相反的入軌誤差對構型產生的影響。

(1)相對方向相反的位置誤差

以任務周期4年為例，分別向三衛星徑向、切向、法向施加均值為100 km的正態分布的，相對方向相同和相反的位置誤差，構型變化如表6所示。

表6 相對位置誤差方向對構型的影響Tab.6 Effect of direction of relative position error on constellation

由于增加的位置誤差大小相等，方向相反，構型標準差相同，反向誤差的擾動大于同向誤差。當航天器受到的位置誤差相對方向不同時，構型產生的擾動更大。

(2)相對方向相反的速度誤差

分別向三衛星徑向、切向、法向施加均值為10 cm/s的正態分布的，相對方向相同和相反的速度誤差，構型變化如表7所示。

表7 相對速度誤差方向對構型的影響Tab.7 Effect of direction of relative velocity error on constellation

由于增加的速度誤差大小相等，方向相反，構型標準差相同，反向誤差的擾動大于同向誤差。當航天器受到的速度誤差相對方向不同時，構型產生的擾動更大。

無論是位置誤差還是速度誤差，當航天器受到的誤差相對方向相同時，誤差對構型的影響明顯小于誤差相對方向相反時的情況。這也為任務入軌工作帶來一些啟示，如果無法減小入軌誤差的絕對值，可以通過使三衛星受到的誤差保持相同方向，減小入軌誤差對構型的影響，保證后續任務順利完成。

5.4 位置速度誤差對構型的影響

入軌位置誤差和速度誤差通常同時存在，方向也可能不同，因此下文將分析兩種不同方向的誤差同時存在對構型產生的影響。以周期4年為例，使切向速度誤差由0.5 cm/s逐漸增加至3 cm/s，并調整徑向位置誤差的大小，以臂長在3×106±3.5×104km內為標準，記錄使構型發散的位置誤差臨界點，如圖3所示。

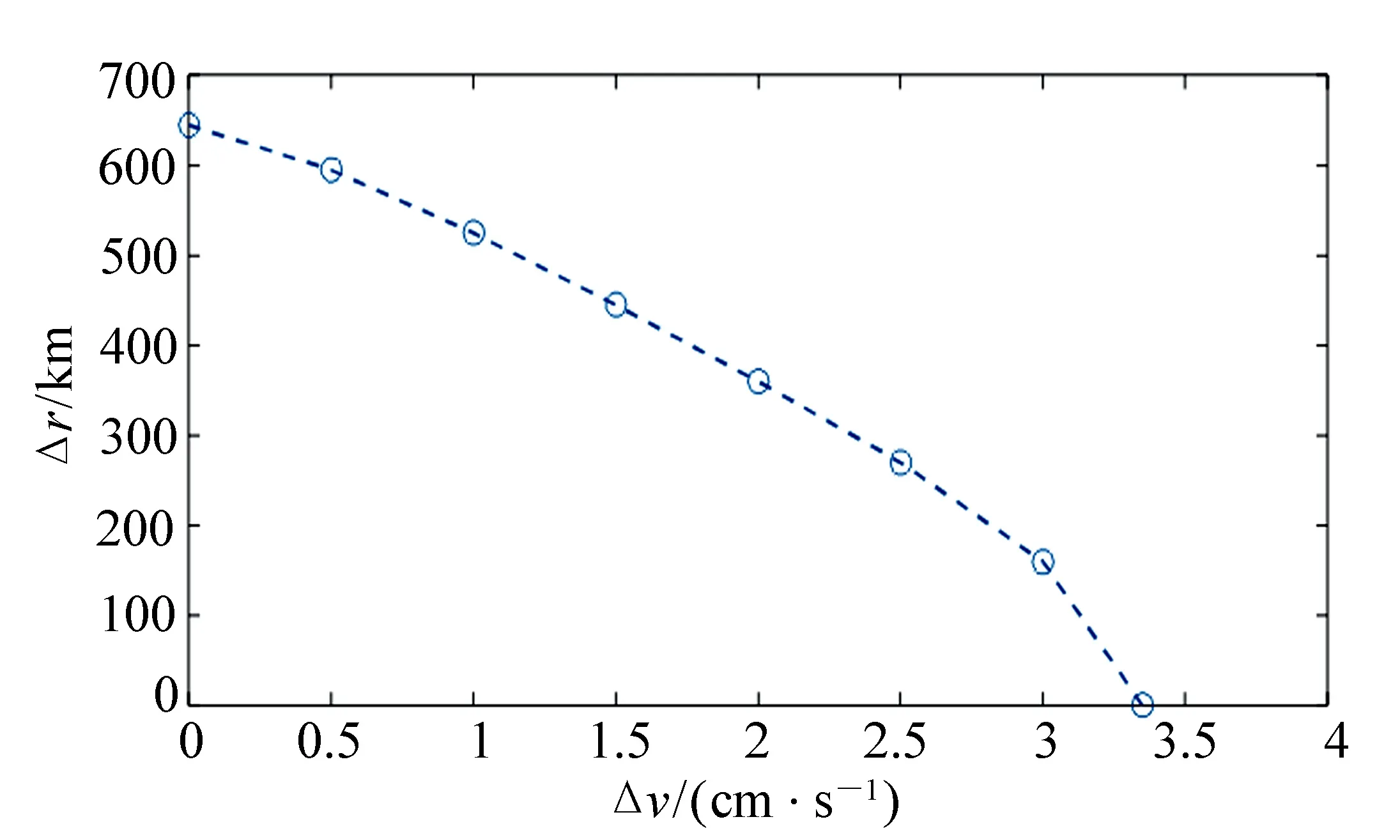
圖3 位置誤差與速度誤差的關系Fig.3 Relationship between position error and velocity error

由圖3可知，速度誤差的影響大于位置誤差，對于同一構型，當速度誤差增大時，為滿足指標要求需減小位置誤差。當速度誤差是0.5 cm/s，位置誤差將超過595 km時構型發散；當速度誤差是3 cm/s，位置誤差超過160 km時構型發散。

6 結 論

本文首先介紹了空間引力波探測任務的動力學模型；運用CADET法提出了空間引力波探測任務入軌誤差傳播方程；進行CADET方法仿真和Monte-Carlo法仿真，并比較二者結果；以本文構型為例，運用CADET方法對入軌誤差的影響進行分析。仿真結果表明：

(1)以Monte-Carlo法結果為標準，CADET法在10年任務周期內與其相對誤差不超過6%， CADET法可以進行有初始誤差情況下的任務過程的誤差傳播分析；

(2)在相同環境下完成Monte-Carlo法1 000次抽樣運算平均用時約為15 min，而CADET法平均用時不超過1 min， CADET法可以實現任務過程中對誤差傳播的快速預測，用時遠小于Monte-Carlo法。

(3)徑向位置誤差和切向速度誤差分別改變了衛星的勢能和動能，對空間引力波探測任務構型影響較大。當誤差的相對方向相同時，對構型的影響小于相對方向不同時，可以通過保持誤差方向相同減小入軌誤差對構型的影響。當周期為4年且同時存在兩種誤差時，位置誤差不超過160 km，速度誤差不超過3 cm/s時，構型仍滿足指標要求。