B電商智能物流中心訂單分波（處理）優化設計

文/陳增坤 余蕾 王旭

1.1問題的提出

1.1.1 問題背景

B電商智能物流中心24小時不間斷接收客戶訂單，并且所有訂單都要求次日達，為了提高多品種、小批量商品的分揀效率和效益，就要首先對商品訂單進行分類處理。同時B電商物流中心采用“貨到人”的自動化揀選系統，即通過智能搬運機器人實現“無人化”搬運作業模式，在方便快捷的同時也帶來了前所未有的挑戰，即要合理調度AGV才能以最低成本實現最大效益，而調度的原則便是基于客戶的訂單信息。因此，智能物流中心的訂單處理是提高揀選效率，降低運營成本，實現規模效益的關鍵環節。

1.1.2 問題分析

在B智能物流中心“貨到人”的作業模式下當已知目前的訂單情況，則其在倉庫中的貨位倉儲信息已知，因此只需要調度AGV小車將訂單品項所在貨架全部搬運到揀選臺即可完成所有的搬運任務。在物流中心目前的運營中按照客戶下單訂單的先后順序劃分訂單波次，發現這種分波模式下，經常造成AGV小車重復搬運貨架，并且由于不同訂單分布的移動貨架距離較遠，使得AGV小車搬運時間較長，且造成運力浪費。為解決上述問題，需要改變當前的訂單處理模式，需要基于訂單相似性來劃分訂單波次，即訂單品項所在統一個貨架的訂單分為一個波次，從而可以減少AGV小車搬運次數，提高揀選效率，降低運營成本。

2.1基于總搬運次數優化的訂單分波模型

2.1.1 訂單分波目標函數

對訂單進行分波是為了提高揀選的效率，更有效地完成揀選作業，為了達到這個目的，通常將訂單分波的目標設置為總的揀選距離最短或者總的揀選時間最短，這兩個目標都為定量并且是容易實現的。在運行的過程中，揀選時間除了與揀選的距離有關外，搬運行走的速度，尋找儲位的時間以及設備的自動化程度等因素有關，這些因素往往與整個系統的硬件以及人員設備有關，不受人力的控制，因此通常情況下，訂單分波的目標可通過減少總的搬運距離來實現。

以揀選距離最短為目標建立數學模型，首先要為AGV小車設置一定的路徑策略，本文采用穿越式策略，這種方式的特點是AGV揀貨小車從通道的一段進入，同時從揀選通道兩側尋找分配的貨架，抬起后從通道另一端離開，由于行走的路徑看上去像是一個“Z”形狀，所以又稱為“Z”形路徑式。

2.1.2 建立模型前的準備

假設AGV揀貨小車從貨架到揀選臺的行駛距離為si，貨架i被搬運的次數為ti，AGV揀貨小車從貨架i到貨架i+1之間行駛的距離為di，從起始點到第一個貨架行駛的距離為d0，從最后一個貨架回到起始點行駛的距離為dn，那么一臺AGV揀貨小車總的搬運

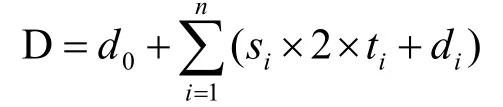
由于AGV搬運小車每次只能搬運一個貨架，因此訂單在分波前與分波后AGV揀貨小車在貨架之間的搬運距離和AGV揀貨小車從初始位置到第一個貨架的距離以及從最后一個貨架返回初始位置的行走距離都是必不可少的，這一點也是與“人到貨”的揀選方式最大的不同，另外，考慮AGV揀貨小車的作業成本，AGV揀貨小車在貨架之間移動時為空車運行，在貨架與揀選臺之間為承載貨架運行，其成本較高，因此認為AGV揀貨小車在貨架與揀選臺之間的搬運距離重要性更高，影響更大。

對AGV揀貨小車的搬運路徑進行分析，綜合考慮以上因素，認為AGV揀貨小車總的搬運距離可以簡化為以下公式：

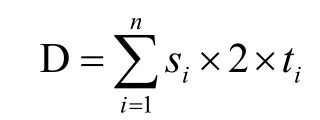
在不考慮AGV揀貨小車在哪一個揀選臺處揀選的情況下，即假設AGC揀貨小車到各個揀選臺的搬運距離相同，由于貨架與揀選臺的位置固定，那么AGV揀貨小車搬運貨架到揀選臺的距離則為固定，因此AGV揀貨小車的搬運距離只與AGV揀貨小車搬運貨架的次數有關，當AGV揀貨小車搬運貨架的總次數最少時，AGV揀貨小車的搬運距離也達到最小。

根據以上分析，同時系統中存在多臺AGV揀貨小車，假設所有小車搬運的總貨架數為N，則本文在對訂單分波的過程中，以所有AGV揀貨小車搬運貨架的總次數最少為目標函數建立數學模型，即目標函數為：

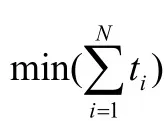
以AGV揀貨小車的搬運次數最少為目標函數建立數學模型，可以為訂單分波作指導，使得分波有所依據。另外以此目標建立的模型一方面不需要事先確定AGV揀貨小車搬運的路徑策略，同時在對模型的求解時，大大減少了計算量，方便了問題的求解。

2.1.3 訂單分波模型設定

為了建模的方便，本文對系統做了如下假設：

（1）一個訂單包含的品項數至少為1。

（2）一個訂單只能被分在一個波次中，不允許分割。

（3）一個貨架在同一個波次中只能被搬運一次。

（4）不存在缺貨的情況。

（5）訂單信息已知，并且訂單品項在貨架中的儲位已知。

（6）AGV小車的搬運路線策略已知。

同時在模型的建立中，設置了如下參數，對其進行了定義。

表1 訂單分波模型所用參數符號及含義

2.1.4 訂單分波模型的建立

根據以上的模型假設及其參數設置，可以將本文研究系統的訂單分波問題描述為：假設有M個訂單需要揀選，共包含W個品項，所有的品項共分布在N個貨架上。現在對這M個訂單進行分波，最終使得AGV揀貨小車搬運貨架的總次數最少。因此，本文中所研究系統的訂單分波問題的數學模型如下：

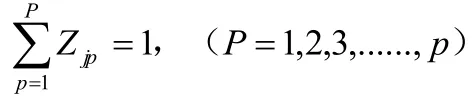
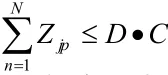
其中為目標函數，表示所有貨架被搬運到次數之和最小。通過每一個波次中每個貨架的搬運次數，即可求得總的搬運次數。約束條件公式表示每個訂單只能被分配到一個波次；公式表示一個貨架在一個波次中只能被搬運1次或者0次；表示一個波次的訂單總數不能超過周轉貨架總的儲位數D·C。

3.1基于節約算法的訂單分波模型求解

訂單分波問題屬于NP～hard問題，而且其隨著訂單數量的增多，其計算量呈指數增長，因此對其求精確解相當困難，在研究中通常選擇啟發式算法對其進行求解。目前對訂單分波問題求解的啟發式算法有多種，可以歸結為種子算法和節約算法兩類。本文應用節約算法來對該系統的訂單分波進行求解，找出優化的分波結果。

節約算法的提出是為了解決運輸問題，在配送的過程中，通常需要完成多個客戶的配送作業，根據客戶的地理位置以及客戶和客戶之間的距離，通過將兩個或兩個以上的客戶合并為一起同時配送，來計算節約的運輸里程，從而找出節約里程最多的客戶合并方式。本文將節約算法應用在配送中心內部AGV揀貨小車的搬運過程，通過計算AGV揀貨小車節約的搬運貨架總次數來對訂單進行分波。

3.2節約算法設計

本文應用C++語言對算法進行編譯求解，節約算法在求解以上訂單分波問題時的計算步驟如下：

（1）在系統中輸入當前所有的訂單信息，以及周轉貨架的儲位數。每一個訂單存放在一個儲位上，周轉貨架的儲位數則代表可以存放的訂單數。

（2）將所有的訂單兩兩組對，計算其組對后的搬運次數的節約量。假設訂單1分布在3個貨架上，訂單2分布在5個貨架上，其中訂單1和訂單2分布的貨架有兩個為重復。若按訂單別來揀選，那么訂單1需要搬運3次，搬運訂單2需要5次；而將訂單1和訂單2劃分為一波后，其重復的貨架只需搬運一次即可，那么兩個訂單總的搬運次數變為6次，則訂單分波后節約的搬運次數就為2次。

（3）將所有的節約次數按由大到小降序排列。

（4）選擇節約次數最大的兩個訂單組合作為初始訂單波量。

（5）首先以這兩個初始訂單組合為基準，找出與這兩個訂單同時位于同一貨架上的訂單，加入到該波次中來：其次再分別以這兩個訂單為基準，比較其與其他訂單的節約量，按節約量由大到小的順序降序排列，選擇節約量最大的訂單劃入該波次。

（6）重復步驟（5），直到該波次的訂單數不滿足周轉貨架所包含的儲位數，那么已完成該波次的分波作業。

（7）不斷的重復步驟（4）～（6），直到所有的訂單都完成分波。

在本文的研究中，通過C++語言對算法進行實現。在實際的應用中，將配送中心收到的顧客訂單進行處理，獲取訂單的貨架信息，將訂單及其貨架信息輸入算法中來，通過運行最終將返回訂單的分波結果。由于在實際的電商配送中心中，訂單量巨大，為了對所用的算法做出更加清晰地解釋，故對實際的配送中心進行了一定的假設并隨機產生少量的訂單來證明算法的有效性。

4.1訂單分波模型效果分析

B電商智能物流中心的分揀作業均在揀選站臺完成，揀選站臺按照波次訂單進行揀選作業，由于不同訂單調度AGV小車搬運的移動貨架不同，而不同移動貨架到各個揀選臺的位置不同，因此將客戶訂單依據AGV小車總搬運距離最短的原則劃分波次，將同一波次訂單分配到同一個揀選站臺，可以有效減少重復搬運、均衡搬運作業，縮短搬運時間，從而降低智能搬運機器人能量損耗、提高揀選作業效率。

5.1結論

在電商智能物流中心的實際運營中，改變傳統的根據時間先后劃分訂單波次的方式，根據訂單相似性，采用基于總搬運距離最短的訂單分波模型，對客戶訂單進行波次分配，可有效解決物流中心存在的智能搬運機器人重復搬運、搬運作業不均衡等問題，實現提高揀選效率，降低運營成本的運營目標，促進物流中心的持續發展。