湍流模型系數不確定度對翼型繞流模擬的影響

趙輝，胡星志，張健，陳江濤，馬明生

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

近些年來，隨著網格生成、流場求解和高性能計算機等學科的快速發展，計算流體力學（Computational Fluid Dynamics，CFD）在工業領域發揮了越來越重要的作用。但是在復雜工程外形的數值模擬過程中，存在著多種來源的不確定性因素，包括幾何外形、網格分布、物理模型及數值計算方法等［1－2］，這使得CFD給出的最終結果也存在著復雜的不確定性。在工程外形的評估或者優化問題中，如果不考慮CFD結果的不確定性，往往不能準確反映復雜物理條件下真實外形的氣動性能。因此CFD的不確定度量化成為近期研究的熱點。

對于工程中的湍流問題，通常都是通過湍流模型來模化雷諾應力，封閉雷諾平均方程。湍流模型是典型的認知不確定性問題。由于對湍流物理本質的理解不完備，導致了湍流模型存在明顯的不確定性。比如模型中的系數很多都是通過試探方法和經驗給出，或者應用漸進性原則通過簡單流動的直接數值模擬或試驗結果來確定的［3］。但是這樣得到的湍流模型并不能保證對所有流動情況都適用。因此評估湍流模型系數的不確定性對數值模擬結果的影響對于CFD的確認問題或者工程外形的設計優化都十分重要。

在常用的不確定度量化方法中，蒙特卡羅（Monte Carlo，MC）方法［4］由于構造簡單、易于實現被廣泛使用。但是MC方法收斂速度慢，需要大量的采樣點才能得到滿足精度要求的結果，因此限制了其在大維度多變量不確定性問題中的應用。隨機譜方法，包括本文要討論的多項式混沌（Polynomial Chaos，PC）方法［5－6］，是一種更有效率的不確定度量化方法。PC方法將整個數值模擬過程認定為一個隨機過程，根據輸入參數的概率密度分布函數，選擇合適的正交基函數，然后將該隨機過程的輸出在基函數構成的譜空間中展開。通過嵌入式或者非嵌入式方法，確定展開式中的自由度，從而得到輸出的完整的譜空間展開和各種統計信息，比如平均值、均方根以及每個不確定輸入變量的全局敏感度指標。使用PC方法的不確定度量化已經有了很多成功的應用［7－14］。

本文使用非嵌入式PC方法研究了Spalart-Allmaras（SA）模型系數的不確定度對RAE2822翼型數值模擬的影響。首先，介紹了非嵌入式PC方法和使用的流場解算工具，研究從單變量入手，考察了卡門常數的不確定度對升阻力系數、壓力分布、摩擦系數分布和馬赫數的影響。然后，同時考慮了SA模型中9個參數的不確定度對數值模擬的影響。最后，給出了研究結論。

1 PC方法展開

PC方法源于Wiener提出的各向同性混沌理論［15］，用于湍流問題中隨機變量的譜空間展開。Ghanem和Spanos將該方法應用到有限元計算中，用來分析固體力學中的不確定性問題［16］。Xiu和Karniadakis將適合高斯隨機過程的 Hermite PC推廣到 Wiener-Askey PC，適用于滿足更一般的概率密度分布的隨機過程［6］。PC方法基于不確定量的譜空間展開，將隨機量分解為確定性的和隨機的兩部分。下面首先從單輸入變量入手，介紹PC方法。

假定隨機的輸入變量ξ，滿足某種概率密度分布f（ξ）。對于任意的隨機輸出變量y（可以是升力、阻力系數等積分量，也可以是流場中某處的壓力系數、摩擦力系數或者馬赫數，或者分離區長度、再附點位置等流場特征量），可以在輸入變量ξ的正交基函數序列構成的譜空間中展開，即

式中：αj為確定性分量，也可稱為自由度；ψj為隨機變量的基函數。理論上式（1）的展開有無窮多項，但是在實際應用中通常將展開在某階次處截斷，即

正交基函數的選擇由隨機輸入變量的概率密度函數決定，滿足：

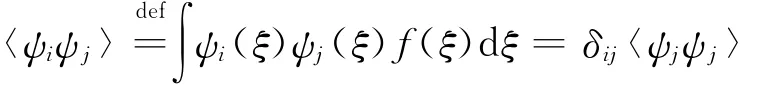
即 ｛ψj，j≥0｝是帶權函數為f（ξ）的正交多項式序列。對于均勻分布的隨機變量，最優的基函數序列是Legendre多項式；而對于正態分布的隨機變量，最優的基函數序列是Hermite多項式。這里談到的最優，是指系統輸出的統計信息隨著多項式階數增加而收斂的速度與理論一致。

根據與求解器耦合方式的不同，可以將PC分為嵌入式多項式混沌（Intrusive Polynomial Chaos，IPC）法和非嵌入多項式混沌（Non-Intrusive Polynomial Chaos，NIPC）法。在IPC中，控制方程中的不確定變量和參數都用其PC展開替代，經過投影之后，得到與原控制方程相似的隨機控制方程，自變量為PC展開中的自由度。IPC需要對現有代碼做較大的改動，不僅工作量大，而且很多時候現有代碼都是封閉的，這限制了IPC在工程問題中的應用。而NIPC無需修改控制方程，將現有的求解器視為一個黑匣子。首先在輸入變量的隨機空間里通過恰當的抽樣方法獲得一系列的采樣點，傳遞給求解器，進行確定性的計算，得到各采樣點對應的輸出響應值，然后通過下文介紹的投影法或回歸法，得到完整的PC展開。本文主要討論NIPC方法。

在NIPC中，主要有兩種方法求解PC展開式中的自由度，投影法和回歸法。投影法利用基函數的正交特性，在式（2）的左右兩側同時乘以ψj，并在ξ的支撐集內積分，利用基函數的正交性質，可以得到

式中：右側積分〈yψj〉可以通過蒙特卡羅積分或者高斯積分得到。當輸入變量的維數較大時，投影法需要大量的采樣點才能滿足精度要求，即使使用稀疏網格的高斯積分，計算量也是巨大的。

在回歸法中，通過確定性的CFD計算得到采樣點 ｛ξ1，ξ2，…，ξN｝對 應 的 響 應 值 ｛y1，y2，…，yN｝。通常情況下，采樣點的數目大于PC展開中自由度的個數。因此形成一個超定方程組Ψα＝Y，其中Ψ是測量矩陣，Ψij＝ψj（ξi）。通過最小二乘法可以得到自由度組成的向量α。本文中自由度計算都是采用回歸法得到。在單變量的不確定度量化中，使用高斯積分法進行結果的對比。

采樣點的數目N跟PC展開中的自由度個數有關，即

式中：n為輸入隨機變量的維數；p為混沌多項式的階數；np定義為過采樣率。Hosder等［17］在計算中發現，np＝2時，PC展開對輸出變量統計信息的近似較好。因此在本文的計算中np均取為2。

得到輸出的PC展開之后，可以根據基函數的正交特性直接得到輸出的均值μ、均方根σ等統計信息，即

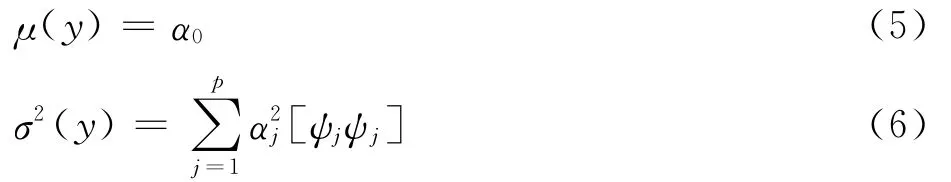
對于多輸入變量的情況，如果各個變量之間是相互獨立的，多維基函數可以直接取為單維基函數的乘積形式，聯合概率密度函數為各變量概率密度函數的乘積。

在多輸入變量的情況下，每個變量的不確定度對系統輸出的不確定度的貢獻大小不一，很多時候需要量化每個變量的相對貢獻大小，分析輸入變量的全局敏感性。Sobol指標［18］提供了工具來量化每個輸入變量對系統輸出方差的貢獻程度。Sobol指標通過Sobol分解得到，是一種基于方差分解的全局敏感性分析方法，其優點是考慮了隨機輸入參數在整個取值范圍內對輸出響應的貢獻以及隨機輸入參數的交互作用［17］。Sobol指標的詳細推導過程和具體形式可以參考文獻［18-19］。

2 計算外形和方法

本文考慮的算例是RAE2822翼型［20］，這是一個典型的超臨界翼型，也是測試CFD程序跨聲速流動模擬能力的經典算例，國內外研究機構針對該翼型開展了大量的風洞試驗和數值模擬研究。本文的計算狀態是：馬赫數Ma＝0.729，雷諾數Rec＝6.5×106，迎角α＝2.31°。使用的網格如圖1所示。

計算使用的程序是課題組自行研發的MFlow［21］。該程序采用基于格心的有限體積法，能夠處理多種網格單元類型（六面體、四面體、三棱柱、金字塔以及使用幾何多重過程中融合產生的多面體）。單元內使用線性重構達到二階精度。梯度計算使用基于格點的格林高斯方法［22］。使用Venkatakrishnan限制器［23］來抑制間斷附近的振蕩。使用Roe格式來計算無黏通量。計算使用一階歐拉后差來推進到收斂狀態，使用局部時間步長加速收斂過程。Jacobian通量使用一階迎風格式得到。

圖1 RAE2822翼型網格分布Fig.1 Grid distribution for RAE2822airfoil

計算使用SA一方程模型［24］，這是在工程界應用非常廣泛的湍流模型。在使用中，假定流動為全湍流，忽略了原始模型中的轉捩項（Trip Term）。因此模型中有9個常數，分別為：cb1、σ、cb2、κ、cw2、cw3、cv1、ct3、ct4。SA 模型的輸運方程形式和模型系數是通過量綱分析、伽利略不變性和部分試驗（包括二維混合層、尾流和平板邊界層等）結果給出的［25］。模型參數的取值存在著一定的不確定度。比較典型的是卡門常數κ，κ描述了邊界層內平均流向速度U＋隨離開壁面距離y＋變化的對數關系［26］。在大氣表層試驗中，κ的值最大為Sheppard測得的0.46，最小為Kansas的結果0.35［27－28］。也有學者指出κ跟雷諾數和壓力梯度有關［29－30］。佘振蘇給出了規范壁湍流中普適卡門常數（κ＝0.45）的定義［31－32］。本文參考了文獻［33］中8個變量的取值范圍，如表1所示，假定每個參數在各自的支撐集內為均勻分布。

表1 SA模型的標準參數和支撐Table 1 SA model closure coefficients and associated support

在進行不確定度量化之前需要指出的是本文側重于研究SA模型系數的不確定度對該算例模擬結果的不確定度影響，沒有考慮網格分布、數值格式等方面的不確定度帶來的影響。

3 不確定度分析

3.1 單變量

從單變量入手，首先研究了卡門常數的不確定度對RAE2822翼型模擬的影響。由于事先無法知曉系統輸出對卡門常數的響應關系，所以假定PC展開的截斷階次分別為p＝1，2，3，4。圖2和圖3給出了翼型升力、阻力系數CL和CD的平均值和均方差值結果。可以清楚地看到，隨著PC展開的階次增加，升力、阻力系數的統計信息變化很小，特別是平均值只有0.01%以內的差別。圖4給出了所有采樣點的升力、阻力系數隨著卡門常數變化的曲線，據此可以推斷升力、阻力系數對卡門常數是近似線性的響應關系。圖5給出了升力、阻力系數的PC展開中各項自由度隨多項式階次的變化，二階和二階以上基函數對應的自由度比一階基函數對應的自由度量值小兩個量級以上，進一步證實了上述結論。

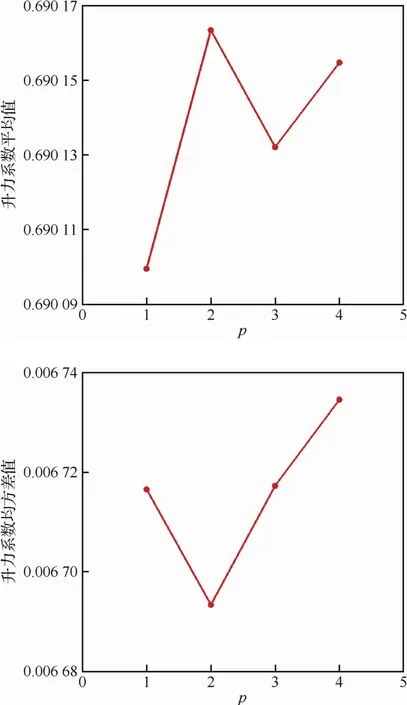
圖2 升力系數的平均值和均方根值Fig.2 Mean values and standard deviations of lift coefficients

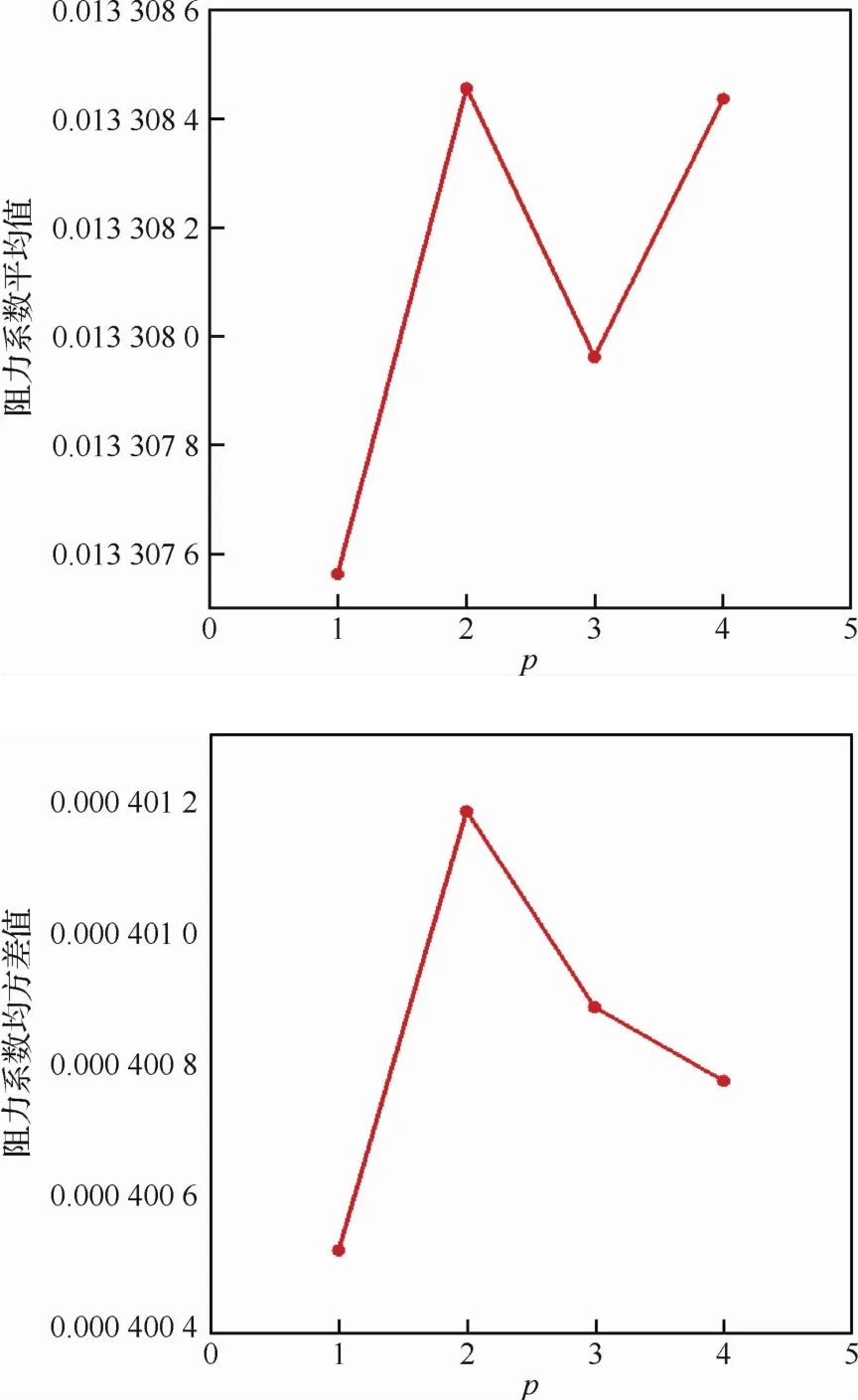
圖3 阻力系數的平均值和均方根值Fig.3 Mean values and standard deviations of drag coefficients

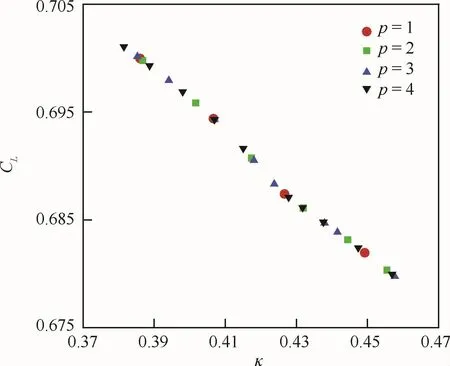
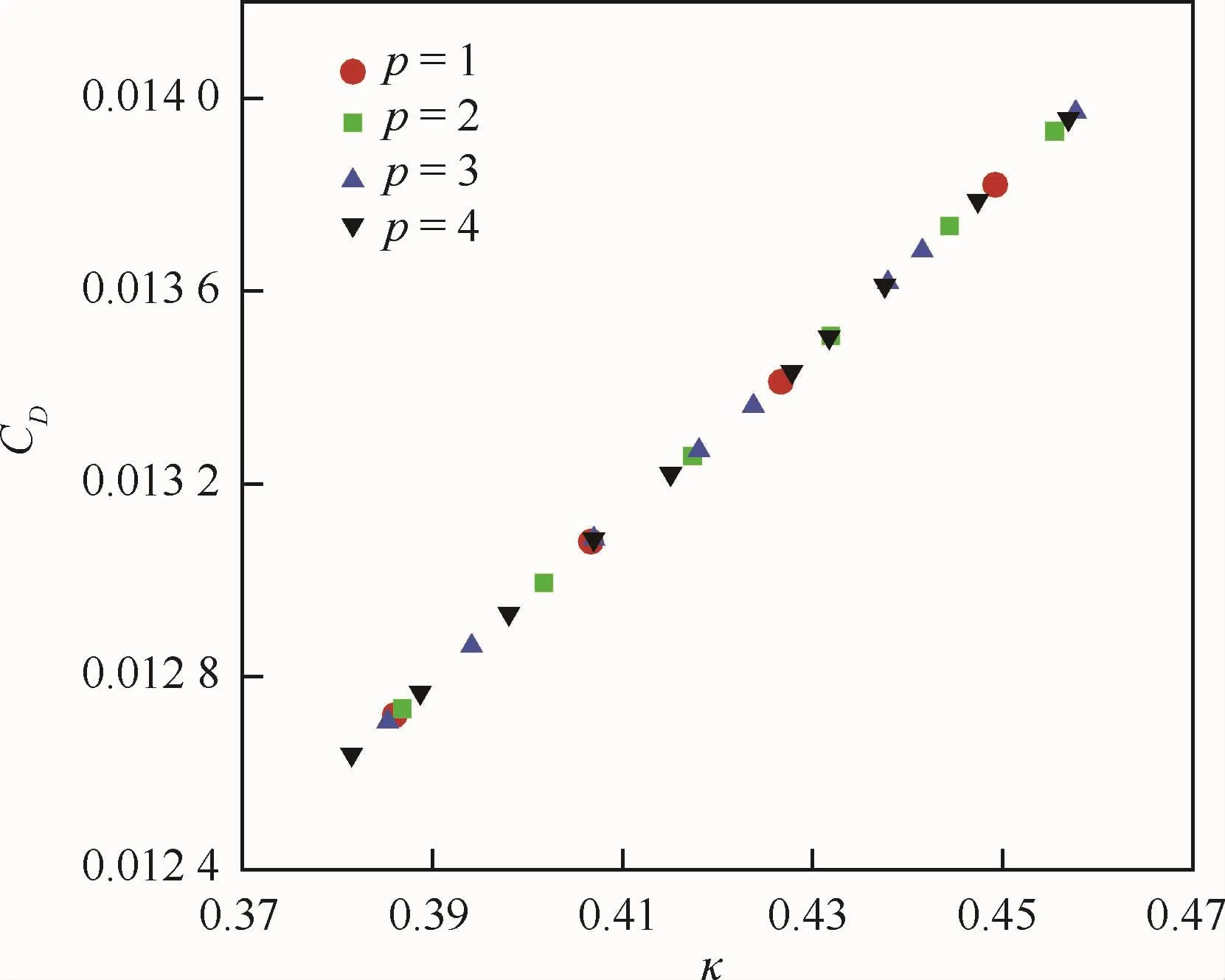
圖4 所有采樣點的升力、阻力系數Fig.4 Lift and drag coefficients for all samples

圖5 升力、阻力系數的自由度Fig.5 Freedoms of lift and drag coefficients

得到輸出的PC展開后，可以預測任意一點的輸入對應的輸出響應。表2給出了κ為模型標準取值0.41時，PC預測值和CFD計算的結果，兩者的誤差幾乎可以忽略不計。說明建立的PC展開能夠準確地描述輸出對輸入的響應。

在單變量情況下，利用高斯積分法和回歸法計算PC展開的自由度，計算量相當。圖6給出了兩種方法得到的升力、阻力系數PC展開中各項自由度，兩者結果也基本一致。

在上面的分析中，系統輸出關注的是升力、阻力系數等積分量，下面進一步討論流場中某處的壓力系數、摩擦力系數或者馬赫數。圖7和圖8給出了壁面壓力分布的不確定度分析結果。其中包括壓力分布的試驗值、平均值、最大值、最小值和方差值。κ的不確定度主要影響翼型上表面，特別是激波附近的壓力分布。減小κ會使得激波位置后移。

圖9給出了壁面摩擦系數Cf預測的均值和極值。κ的不確定度影響著翼型上、下表面的摩擦系數預測。當κ在其支撐集內取最小值時，預測的壁面摩擦系數最小；當κ取最大值時，預測的壁面摩擦系數最大。對于激波位置和壁面摩擦系數隨著κ變化的原因，可以從湍流渦黏系數υt的變化來解釋。在簡單平面剪切湍流的等雷諾應力層，渦黏系數υt與κ成正比［3］，即υt＝κuτd，其中uτ為壁面摩擦速度，d為到壁面的距離，因此減小κ會得到較小的渦黏系數。圖10給出了κ取最大值時計算的渦黏系數與κ取最小值時的渦黏系數的差值云圖。從圖可以清楚地看到，在流場的大部分區域，減小κ會減小渦黏系數，從而導致預測的壁面摩擦系數減小，同時邊界層內流體微團動能損失較少，抵御逆壓梯度的能力更強，預測的激波位置因此后移。

表2 PC展開與CFD得到的升力、阻力系數比較Table 2 Comparison of lift and drag coefficients obtained with PC and CFD

圖6 升力、阻力系數的自由度比較（回歸法和高斯積分法）Fig.6 Comparison of freedoms of lift and drag coefficients（regression method and Gauss integration method）

圖7 單變量下的壓力分布Fig.7 Pressure distribution under single variable

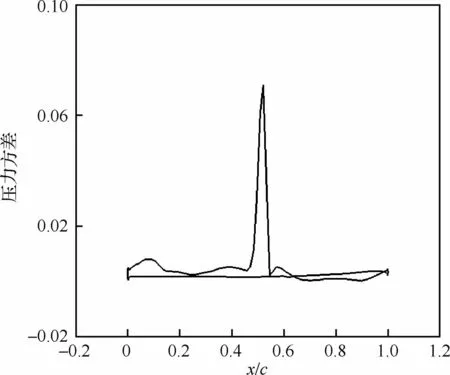
圖8 壓力分布的方差Fig.8 Variance of pressure distribution

圖11是馬赫數方差的云圖，κ的不確定度主要影響上表面激波位置的預測，從而也會影響激波附近馬赫數的預測。

圖9 單變量下壁面摩擦系數的平均值和極值Fig.9 Mean and extreme values of skin friction coefficient under single variable

圖10 渦黏系數差值云圖（υt｜κ＿max－υt｜κ＿min）

圖11 馬赫數方差云圖Fig.11 Contours of variance of Mach number

3.2 多變量

通過上面的分析可以知道κ的變化對激波位置和壁面摩擦預測的影響，也得到了系統輸出對κ的響應。下面同時考慮SA模型中9個參數的不確定度對數值模擬的影響。計算中PC展開的階次為p＝2，考慮了任意兩個參數的聯合影響。在9維空間中，采樣點通過拉丁超立方抽樣得到。

表3給出了升力、阻力系數預測中9個參數各自的Sobol指標，按照貢獻大小排序。與文獻［33］的結果存在明顯的差異，主要表現為在本文的計算中ct3、ct4這兩個參數對升力、阻力系數方差的貢獻很小。這是因為本文使用的SA模型忽略了原始模型中的轉捩項，由此很多學者指出包含ct3、ct4的ft2也是可以忽略的。同時cb2、cw3這兩個參數的貢獻也是可以忽略不計的。cb1、σ、κ、cw2、cv1這5個參數對于升力、阻力系數的不確定度影響都相對比較大，κ是其中貢獻最大的參數，其他4個參數的貢獻大小排序并不完全一致。

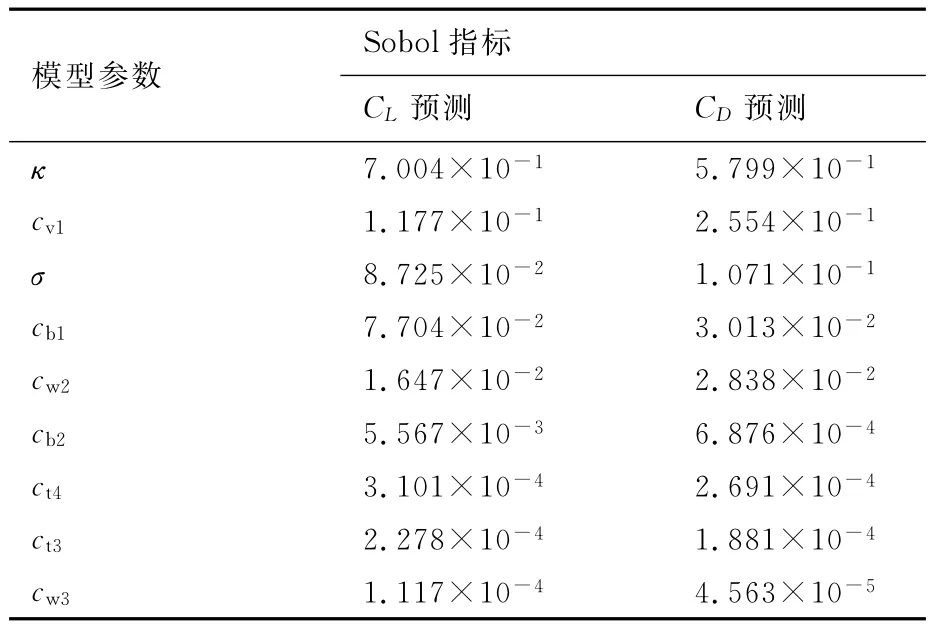
表3 升力、阻力系數預測中9個參數的Sobol指標Table 3 Sobol indices of 9closure coefficients for lift and drag coefficients

通過升力、阻力系數的響應，可以得到其平均值、均方差等統計信息，如表4所示。其中升力系數 的 最 大 值 取 在 ｛cb1＿max、σ＿max，κ＿min，cw2＿max，cv1＿max｝，最 小 值 取 在 ｛cb1＿min，σ＿min，κ＿max，cw2＿min，cv1＿min｝。阻力 系 數 的 最 大 值 取 在 ｛cb1＿max，σ＿max，κ＿max，cw2＿max，cv1＿min｝，最 小 值 取 在 ｛cb1＿min，σ＿min，κ＿min，cw2＿min，cv1＿max｝。ct3、ct4、cb2、cw3這 4 個 參 數 在支撐集內變化對升力、阻力系數影響很小。

表4 升力、阻力系數的均值和均方差值Table 4 Mean value and standard deviation of lift and drag coefficients

得到輸出的PC展開后，可以預測任意一點的輸入對應的輸出。表5給出了模型參數為標準取值時，PC預測值和CFD計算的對比，其中，CDp為壓差阻力，CDf為摩擦阻力，兩者誤差很小。說明建立的PC展開能夠準確地描述輸出對多變量輸入的響應。

表5 PC展開與CFD得到的升力、阻力系數比較Table 5 Comparison of lift and drag coefficients obtained through PC and CFD

通過確定的CFD計算可以得到壁面壓力分布響應。圖12給出了壓力的試驗值、平均值和極值。在機翼的上表面，特別是激波附近，壓力的不確定度表現顯著。上表面壓力極小值取值在｛cb1＿max，σ＿max，κ＿min，cw2＿max，cv1＿max｝，極 大 值 取 值 在｛cb1＿min，σ＿min，κ＿max，cw2＿min，cv1＿min｝，與 升 力 系 數 的情況類似。圖13給出了9個輸入參數對壓力方差的貢獻度。與升力、阻力系數貢獻結論一致，ct3、ct4、cb2、cw3這4個參數對壓力的不確定度貢獻相對較小，其他5個參數，特別是σ、κ貢獻較大。

圖14給出了壁面摩擦系數的平均值和極值。與壓力分布不同的是，ct3、ct4、cb2、cw3這4個參數在機翼的前緣對摩擦系數的不確定度也有著不可忽視的貢獻，如圖15所示。

Fig.12 Pressure distribution under multi-variables

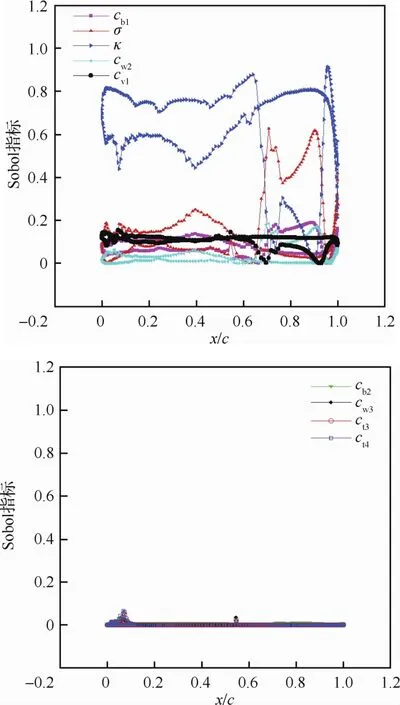
圖13 壓力分布的Sobol指標分布Fig.13 Sobol index distributions for pressure distribution

圖14 多變量下壁面摩擦系數的平均值和極值Fig.14 Mean and extreme values of skin friction coefficient under multi-variables

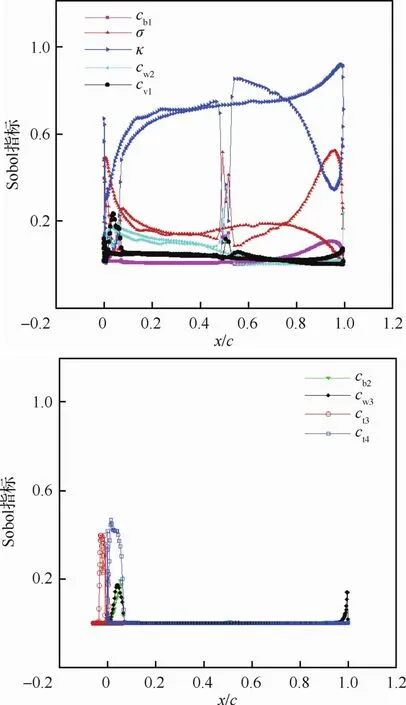
圖15 壁面摩擦系數分布的Sobol指標分布Fig.15 Sobol index distributions for skin friction coefficient distribution

SA模型中的9個參數綜合影響了湍流渦黏系數的生成、擴散和耗散。比如參數cb1與渦黏系數的生成項和耗散項（部分）成正比，該參數的改變會同時增大或者減小生成和耗散，對渦黏系數的綜合作用尚且未知。從理論上很難得到參數變化對渦黏系數影響的規律，而且很可能在流場不同區域產生相反的結論。因此本文只對κ、ct3、ct4這3個參數引起的不確定度進行簡單分析，其他參數的影響需要繼續深入研究。

參數ct3、ct4對模型的影響體現在生成衰減項ft2里。本文使用的SA模型忽略了原始模型中的轉捩項，由此ft2只在翼型前緣附近渦黏系數很小的區域發揮作用，在其他區域的邊界層內基本沒有作用。因此ct3、ct4的不確定度對模擬的影響主要體現在前緣附近，特別是對摩擦系數的預測。

圖16給出了馬赫數的平均值和方差的云圖，在激波附近馬赫數表現出較大的不確定度，與設想的一致。

4 結 論

本文使用非嵌入式多項式混沌方法研究了湍流模型系數的不確定度對RAE2822跨聲速翼型繞流模擬的影響。

Fig.16 Contours of mean values and variances of Mach number

1）從單輸入變量入手，研究了卡門常數κ的不確定度對數值模擬的影響。研究發現升力、阻力系數對κ是近似線性的響應關系。在單變量情況下，利用高斯積分法和回歸法計算PC展開的自由度，兩者結果也基本一致。κ的不確定度主要影響翼型上表面，特別是激波附近的壓力分布，同時還影響翼型上、下表面的摩擦預測結果和激波附近馬赫數的預測結果。κ減小時，預測的激波位置后移，摩擦系數預測值變小。

2）同時考慮模型中9個參數的不確定性帶來的影響。通過升力、阻力系數預測中9個參數各自的Sobol指標可以發現，ct3、ct4、cb2、cw3這4個參數對升力、阻力系數方差的貢獻很小，可以忽略不計。其他5個參數對于結果的不確定度影響都相對比較大，κ是其中貢獻最大的參數。建立的PC能夠給出壁面壓力分布、摩擦系數分布和馬赫數分布的不確定度。

3）通過PC展開和CFD計算的對比證實了建立的PC展開能夠準確地描述輸出對輸入的響應。這為量化計算結果的不確定度提供了切實可行、有較高效率的解決方案。需要指出的是本文的計算只考慮了RAE2822跨聲速翼型模擬的單一計算狀態，影響規律是否可以推及其他工況和算例需要進一步檢驗。