風洞試驗模型表面的熒光油膜路徑運動速度測量

鄒易峰，張征宇＊，王學淵，黃敘輝范金磊

1.西南科技大學 信息工程學院，綿陽 621000

2.中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

摩阻是表面摩擦阻力的簡稱，是飛行器飛行時總阻力的重要組成部分［1］。降低摩阻不僅意味著飛行器的油耗下降、航程增加，對于高超聲速飛行器還意味著其表面熱流降低，防熱材料重量減少，有效載荷增加［1－4］。例如，對現代寬體大型民航客機巡航阻力分析，發現巡航飛行時摩阻可占總阻力的50%，遠超其他阻力項，同時，摩阻每下降1%，油耗和碳排放量可下降0.625%，因此減少摩阻對改善飛機性能和降低成本都具有重要意義［5－6］。對于高超聲速飛行器，其摩阻最大時可占總阻力的50%以上，直接關系到其有效航程，甚至影響到超燃沖壓發動機的推阻平衡，從而嚴重制約高超聲速飛行器的性能［7］。因此，高精度的全局摩阻測量技術對于飛行器的減阻研究與設計不可或缺。

另一方面，準確的全局摩阻測量數據與清晰的摩阻線圖譜對于空氣動力學基礎研究也至關重要，既能為創建與驗證近壁湍流模型提供依據，又能為物面流動特性、分離特性以及渦形成機理研究等提供重要的手段與數據，同時也是考核湍流理論研究（如模式理論）與檢驗數值模擬結果的重要依據之一［8－12］。

現有的全局摩阻測量技術有蒸發膜、液晶膜、油膜以及基于微機電系統（Micro-Electro-Mechanical System，MEMS）的摩擦天平、熱膜等。雖然基于微機電系統的摩擦天平與熱膜在未來有巨大的潛力，但現階段面臨制造難、成本高、空間分辨率低等問題［13－17］；液晶膜的測量結果對光源和觀測角度的敏感阻礙了其運用到外形復雜的試驗模型，加之其顏色變化不僅與摩阻相關還與測量的溫度相關，而且為了定量測量表面摩阻，需要5～10個相機以獲得足夠多方位角的圖像數據，而現有高速風洞試驗條件難以滿足［18－19］；基于干涉的油膜摩阻測量能實現較高空間分辨率的全局測量，但為了獲得必要的反射特性，試驗模型須具備特殊材質的物面，粗糙的物面不適用于干涉法，盡管用x-y探測器替代記錄干涉圖像的光學器件可消除其對模型表面的特殊要求，但仍難滿足高分辨率、復雜形面的摩阻分布測量需求［20－24］；表面應力敏感膜通過橫向變形和垂直變形來測量摩阻和正壓力，但這兩個方向的變形存在一定的耦合干擾［25－26］。

熒光油膜全局摩阻測量法［27］因具有設備簡單（僅需紫光激發光源、相機與鏡頭）、空間分辨率高、對模型物面無特殊要求等優點，成為研究的熱點［28-33］。該法通過熒光油膜控制方程［11］，建立熒光油膜（受紫外光激發的輻射光成像）灰度與其運動速度的關系，獲得油膜在表面摩阻、壓力梯度、體積力以及表面張力等作用下其厚度h隨時間變化的關系，由于摩阻僅與油膜厚度的一次方h相乘，其他項則是與油膜厚度的二次方h2相乘，且兩項乘積互不相關，因此，當油膜厚度h極小時，表面摩阻將占主導地位，壓力梯度、體積力及表面張力相對表面摩阻而言可以忽略不計，可簡化得出熒光油膜摩阻測量模型［27－30］。熒光油膜全局摩阻測量需要先用光流法求出熒光油膜路徑運動速度，再將其和油膜厚度h代入測量模型［27－30］以獲得摩阻。因此，熒光油膜路徑運動速度測量的精準度對于全局摩阻測量至關重要。但現有熒光油膜全局摩阻測量法尚難用于高速風洞試驗，尤其無法用于試驗模型存在運動的環境（如動態風洞試驗環境、模型振動環境），而且試驗模型在非定常氣動力或氣流脈動作用下或多或少存在振動，原因在于：中國現有試驗模型大多通過桿式懸臂梁承載結構與風洞中部支架相連，因支撐剛度不足出現振動。因此，從模型表面熒光油膜時序圖像中解得的熒光油膜路徑運動速度必然含有模型運動速度，特別是當模型運動速度較大時，還將導致相鄰時序圖像亮度不變性和時間持續性（小移動）假設失效，致使光流約束方程求解得到的全局摩阻測量數據出現較大誤差，而且熒光油膜解在一般條件下的準自相似特性［30］不再成立，即簡單地將不同時段獲得的多對解進行融合，不能再提高測量結果的分辨率和精度。雖然，通過圖像空間降采樣（即犧牲圖像的空間分辨率將多個像素融合為一個像素）可使其滿足光流法求解條件，但解得的結果仍是熒光油膜路徑運動速度與模型運動速度之和，并且丟失了物面流動的精細結構。

為此，本文面向生產型風洞試驗環境，研究模型振動與其表面熒光油膜路徑運動的解耦方法，以得到定量、清晰、準確的表面摩擦應力線圖譜與油膜路徑運動速度場。

1 理論基礎

1.1 熒光油膜的路徑運動速度

來流在試驗模型表面產生平行于表面的切向摩擦應力τ和垂直于表面的壓力。油膜在τ和體積力作用下在模型表面流動，將其速度記為熒光油膜的路徑運動速度U1；由于風洞試驗中模型在氣流脈動作用下或多或少存在振動，模型振動必然帶著熒光油膜一起運動，將其速度記為U2。鑒于高速風洞試驗中，來流速度遠遠大于U2，即U2在測量表面誘發的表面摩擦應力τ0非常小，可將τ0產生的熒光油膜流動忽略不計。因此，利用熒光油膜時序圖像解得的油膜速度為

式中：U3為油膜自身慣性力導致的運動速度。考慮到測量時熒光油膜的Reynolds數非常小，即油膜的慣性力與黏性力相比可以忽略不計［33］，所以可以忽略U3，得出

由此可見，只有在U2遠小于U1時，方可忽略U2的影響，但在熒光油膜全局摩阻測量法中，尤其是油膜較薄時，U1相對于U2是個小量，因此，模型振動與其表面熒光油膜路徑運動的解耦攸關全局摩阻測量的精準度。

1.2 離散匹配原理

薄油膜中熒光材料受紫光激發后，對模型表面明顯的背景紋理（如人工網格線或其他典型特征）的成像影響極小，為此本文利用視頻測量的同名點圖像匹配方法［31－36］，利用模型表面的背景紋理作為模型運動與油膜路徑運動的解耦基準。由于三維空間到CCD上投影成像具有非線性特性［31－36］，本文將時序圖像離散為網格塊區域，利用數字圖像相關法進行離散匹配，獲得相鄰時序圖像的離散映射矩陣，并基于模型運動的連續性，對離散映射矩陣進行平滑優化，得到連續平滑的離散映射矩陣，進而在圖像空間實現模型運動與熒光油膜路徑運動解耦。

圖1所示為油膜模擬圖像（230pixel×230pixel），將圖像離散化為相同大小且不重疊的離散網格，對圖1（b）施加1°旋轉量以模擬模型振動。當時間間隔Δt很小時，對于相鄰幀圖像上具有相同編號的離散網格區域，若網格足夠小，則網格內各像素點運動速度差異非常小，可用給定的網格中心特征點Pi，j（如圖1中綠色標記點所示，其中i，j為圖像離散網格行列編號）的速度表示該離散網格的速度。以Pi，j為中心，以2倍網格邊長為匹配窗口邊長，設定合適搜索域參數，匹配圖像It1上的Pi，j特征點在后序圖像It2上的對應點坐標位置 （x′，y′），采用的相關匹配函數為

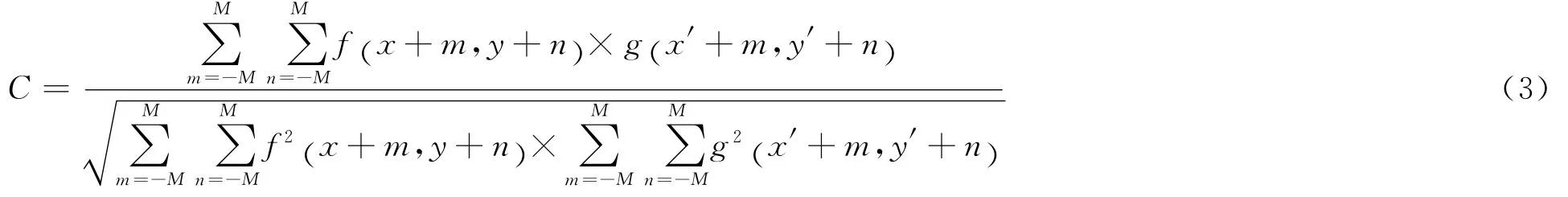
式中：C為匹配度；f（x，y）為圖像It1上特征點Pi，j坐標 （x，y）處的灰度值；g（x′，y′）為圖像It2坐標 （x′，y′）處的灰度值。通過式（3）搜尋計算Pi，j在圖像It2上的最佳匹配點，即匹配度C值最大的點。

根據圖像It1上的特征點及其通過離散匹配計算得到的圖像It2上的對應特征點，本文提出基于鄰域4特征點的相鄰時序區域圖像映射矩陣計算方法，如圖1所示，計算It2到It1區域圖像的映射矩陣為

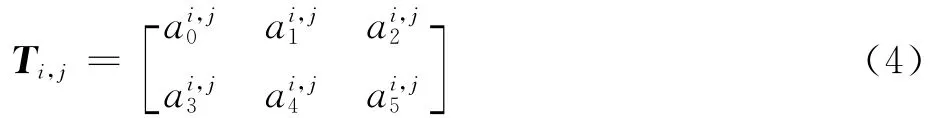
式中：ai，jm（m ＝0，1，…，5）為映射矩陣系數。

將鄰近4個特征點代入

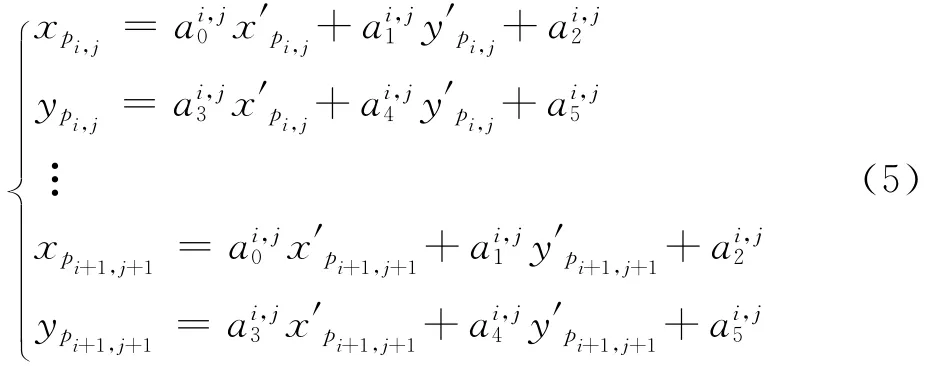
利用最小二乘法求解式（5）得到離散網格區域的映射矩陣。與利用單個特征點的運動來代表離散網格的運動相比，采用鄰域4特征點求取映射矩陣的方法，可充分利用明顯的背景特征，同時求得的映射矩陣包含鄰近4個離散網格的運動信息，其準確性更高。

圖1 圖像It1及圖像It2Fig.1 Image It1and image It2

1.3 映射矩陣全局平滑原理

圖像It2經映射矩陣變換后，可能出現離散網格邊界與其相鄰離散網格邊界的位移不相等，進而導致映射變換后的圖像I′t2上出現灰度不連續，因此，本文對映射矩陣施加全局平滑約束。

對于圖像It2中給定的離散網格，網格內所有像素點對應同一映射矩陣Ti，j，根據離散映射矩陣Ti，j構建全局映射矩陣：

為了使平滑后的映射矩陣S′盡可能地接近于原矩陣S，可構建映射矩陣的全局平滑模型

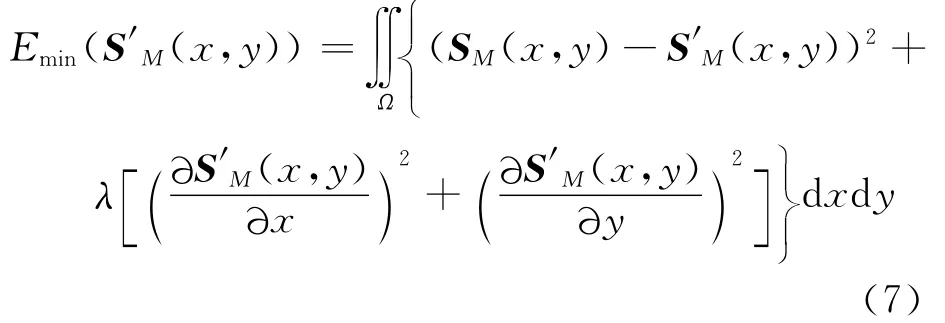
為了便于表述，記SM（x，y）與S′M（x，y）分別為SM和S′M，M 表示映射矩陣Ti，j中的元素序號（M ＝0，1，…，5），Ω表示能量函數的積分范圍，（x，y）為離散矩陣的行列號。該模型包括兩項：前一項為數據項，控制全局平滑前后SM和S′M間的最小差值；后一項為平滑約束項。λ為Lagrange乘數，用于平衡誤差數據項與平滑約束項之間的權重關系，λ越大，得到的映射矩陣S′M越平滑。

式（7）將數據項與平滑約束項一起構成能量函數E（S′M），使得能量函數E（S′M）取得最小值Emin（S′M）的S′M就是最終的解，這是一個求取復雜方程的極小值問題，因此本文采用變分技術進行求解。

考慮到求取的對象為S′M，而S′M取決于位置變量（x，y），因此主要考慮以多元函數S′M為自變量的積分型泛函的極值問題，將式（7）寫成泛函形式為

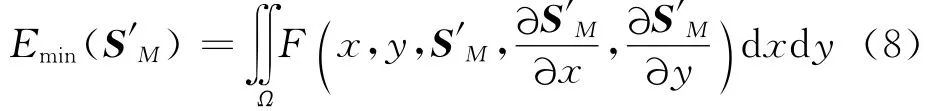
函數F為泛函Emin（S′M）的核：

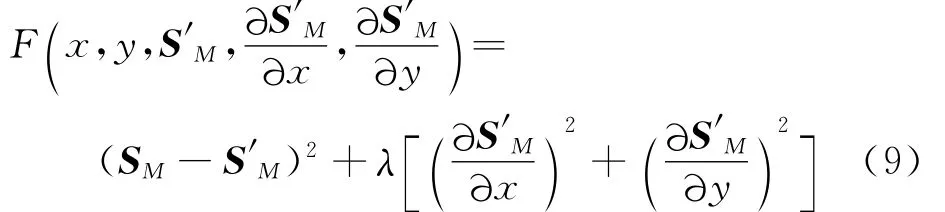
對泛函Emin（S′M）進行變分求解，其解滿足歐拉-拉格朗日（Euler-Lagrange）方程：

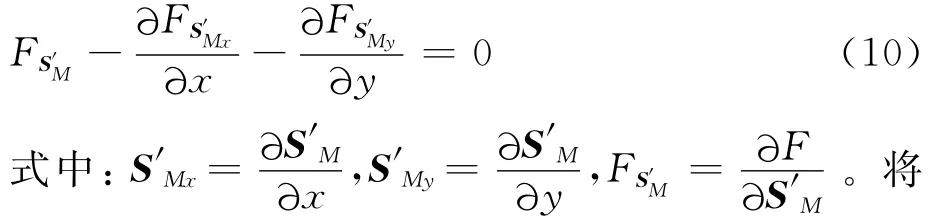
函數F代入式（10）整理可得

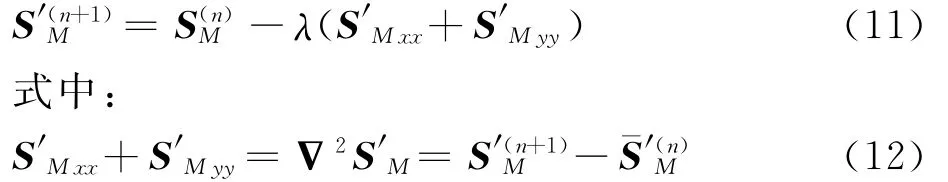
即用某一點的灰度值與周圍灰度平均值之差表示拉普拉斯算子，可得

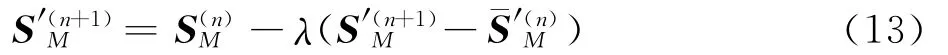
采用迭代法可以求解得到平滑映射矩陣S′M。

1.4 模型運動與熒光油膜路徑運動解耦

根據S′M對圖像It2進行映射變換，得到運動解耦后圖像I′t2的像素坐標計算式為

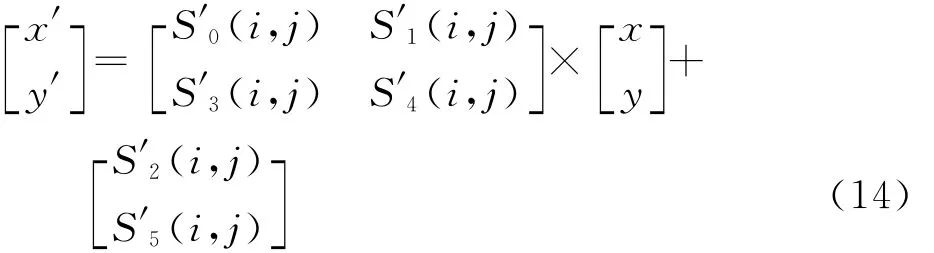
此時，I′t2與圖像It1滿足光流法求解油膜路徑運動速度的灰度連續性假設。

2 數值仿真及試驗

參考文獻［30］中熒光油膜圖像的模擬方法，用圖2（a）與圖2（b）所示的熒光油膜模擬圖像（230pixel×230pixel）表征給定的速度場：

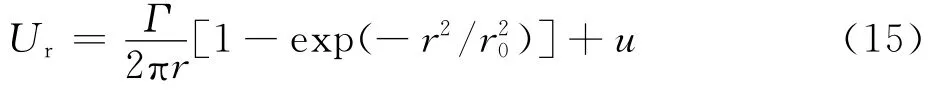
即將一由左至右的均勻速度場u和Oseen渦對速度場疊加，r為圖像某像點離渦核的距離，渦強度Γ 為2 000pixel2／s，r0為20pixel，u為10pixel／s，其速度場疊加效果圖如2（c）所示。取演化時間為0.000 1s，對圖2（a）利用雙線性插值，演化1 000步得到0.1s后如圖2（b）所示熒光油膜模擬圖。

圖2 熒光油膜模擬圖像及人工合成Oseen渦對速度場Fig.2 Fluorescent oil film simulation images and synthetic Oseen vortex pair velocity field

對圖2（a）和圖2（b）添加不同灰度對比度的人工網格線（網格線寬度與相鄰兩網格線間距之比為1∶20），以研究其對離散匹配精確度的影響。定義灰度對比度為

式中：g′為人工網格線灰度值；g（x，y）為圖2（a）與圖2（b）上 （x，y）坐標處灰度值。當Cg為最大值1，即網格線灰度g′最大值為圖像灰度均值時，說明網格線灰度值g′與圖像灰度均值最接近，網格紋理不明顯；反之，當Cg值越接近0時，網格紋理越明顯。

對圖2（a）添加Cg分別為0.8、0.6、0.4、0.2與0的人工網格線，其中Cg＝0的人工網格線如圖3（a）所示；同理，對圖2（b）添加Cg分別為0.8、0.6、0.4、0.2與0的人工網格線，并使圖像繞其中心坐標順時針旋轉1°，得到如圖3（b）～圖3（f）所示的圖像，旨在評估Cg對離散匹配精確度的影響。

圖3（b）～圖3（f）經離散圖像匹配、映射變換后得到映射圖像，對映射圖像采用光流法求解速度場，取過Oseen渦對渦核直線上的x方向速度，與理論結果的對比如圖4所示，其測量誤差見表1。

如圖4所示，在邊界A、B區域，光流法求解結果與理論結果存在明顯差異，原因在于：求取圖像邊界的灰度梯度時，由于缺乏圖像邊界外的灰度信息，本文通過復制邊界值進行填充以計算圖像邊界處的灰度梯度，從而在邊界處產生誤差，因此，在分析對比結果時，可忽略邊界值（如圖3（a） 所示，x≤10pixel，x≥220pixel）對試驗的影響。

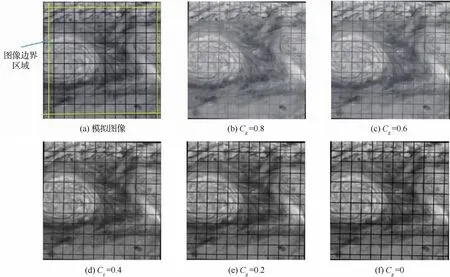
圖3 不同Cg值下的圖像Fig.3 Images under various Cgvalues

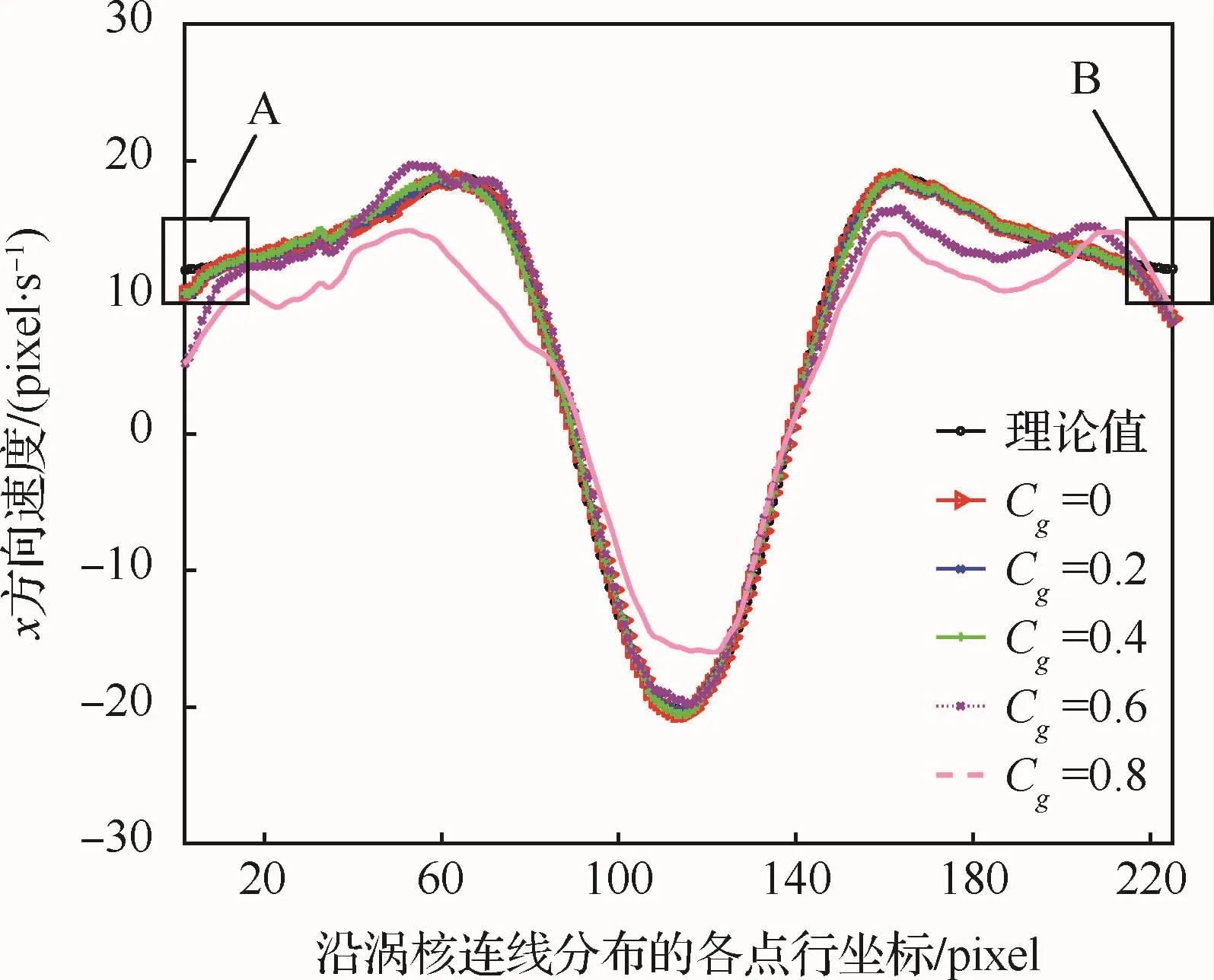
圖4 不同Cg下沿Oseen渦核分布的測量速度Fig.4 Measurement velocities distributed along Oseen vortex cores under various Cg

表1 不同Cg下沿Oseen渦核分布的最大速度相對誤差Table 1 Maximum velocity relative errors distributed along Oseen vortex cores under various Cg

如表1所示，對于Cg為0.4、0.2和0的圖像，經離散匹配、映射變換后，與理論結果相比，其光流求解速度最大相對誤差為3.6%；而對于Cg為0.6與0.8的圖像，最大相對誤差分別達到了21.9%和49.9%，表明：網格線灰度與圖像灰度越接近，離散匹配過程中出現特征點匹配錯誤的概率越大，得到的映射矩陣誤差也越大，此時，利用光流法計算得到的速度與理論結果差異也越大。因此，本文在后續試驗中添加Cg＝0的人工網格線。

為測試本文算法解耦模型振動與油膜路徑運動的效果，如表2所示，對圖2（b）添加不同平移旋轉參數以模擬試驗模型的振動，其中，定義平移量為圖像在x、y方向上的移動量，旋轉量為圖像繞其中心位置的旋轉角度，得到圖5（a）所示圖像。

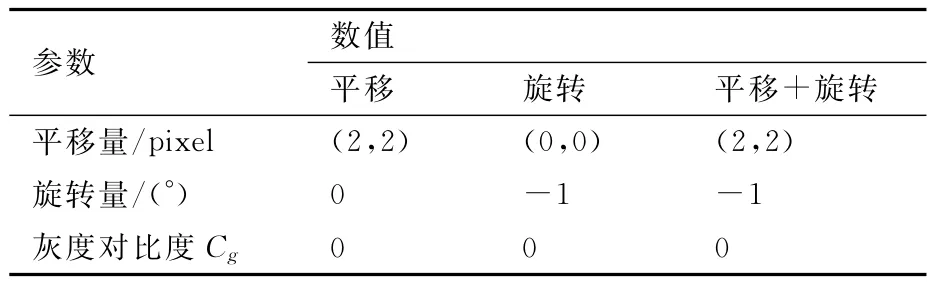
表2 對圖2（b）添加不同平移旋轉參數Table 2 Parameters for translation and rotation of Fig.2（b）

圖5（a）是未經離散匹配、映射變換的圖像，直接用光流法解得的流線圖如圖6（a）所示，與圖2（d）理論結果不相符，說明小幅度平移旋轉量對速度求解準度的影響巨大；圖5（b）是經離散匹配、映射變換的圖像，用光流法解得的流線圖如圖6（b）所示，與圖2（d）相符；圖7為離散匹配后未進行全局平滑優化的圖像經光流法解得的流線圖，與圖6（b）相比效果明顯變差。

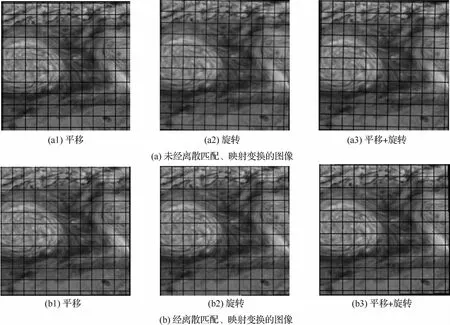
圖5 不同平移旋轉參數下油膜圖像及其運動解耦圖像Fig.5 Oil film images and movement decoupling images under different translation and rotation parameters

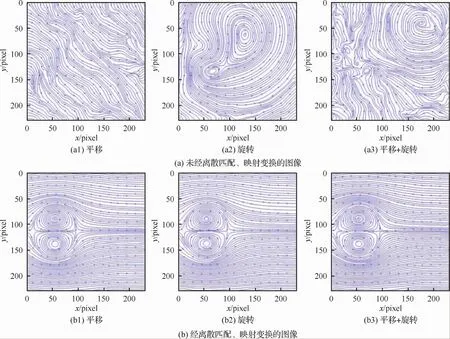
圖6 光流求解速度流線Fig.6 Velocity streamline by optical-flow solutions

如圖8所示，取過Oseen渦對渦核直線上的x方向速度與圖2（c）理論結果對比，誤差如表3所示。其中，“原始圖像”指對圖2（a）與圖2（b）直接采用光流法求解，其速度與理論值的最大相對誤差為3.5%；“平移旋轉圖像”為圖6（a3）的光流求解速度，與理論結果的最大相對誤差為148.4%，這是因為：在旋轉平移條件下，光流求解得到的速度包含模型運動速度，與油膜路徑運動速度有巨大差距；“離散匹配圖像”是圖7光流求解速度與理論結果的比較，其最大相對誤差為91.5%，這是因為：修正旋轉平移時，映射矩陣未進行全局平滑優化，導致相鄰離散網格邊界間的位移不相等，造成圖像灰度不連續，進而導致光流求解的速度與理論值之間誤差巨大；“離散匹配并平滑處理”是圖6（b）與理論結果的比較，其最大相對誤差為4.1%，與“原始圖像”相比，經離散匹配、映射變換修正旋轉平移后，最大相對誤差僅增加0.6%，說明本文算法是正確有效的。

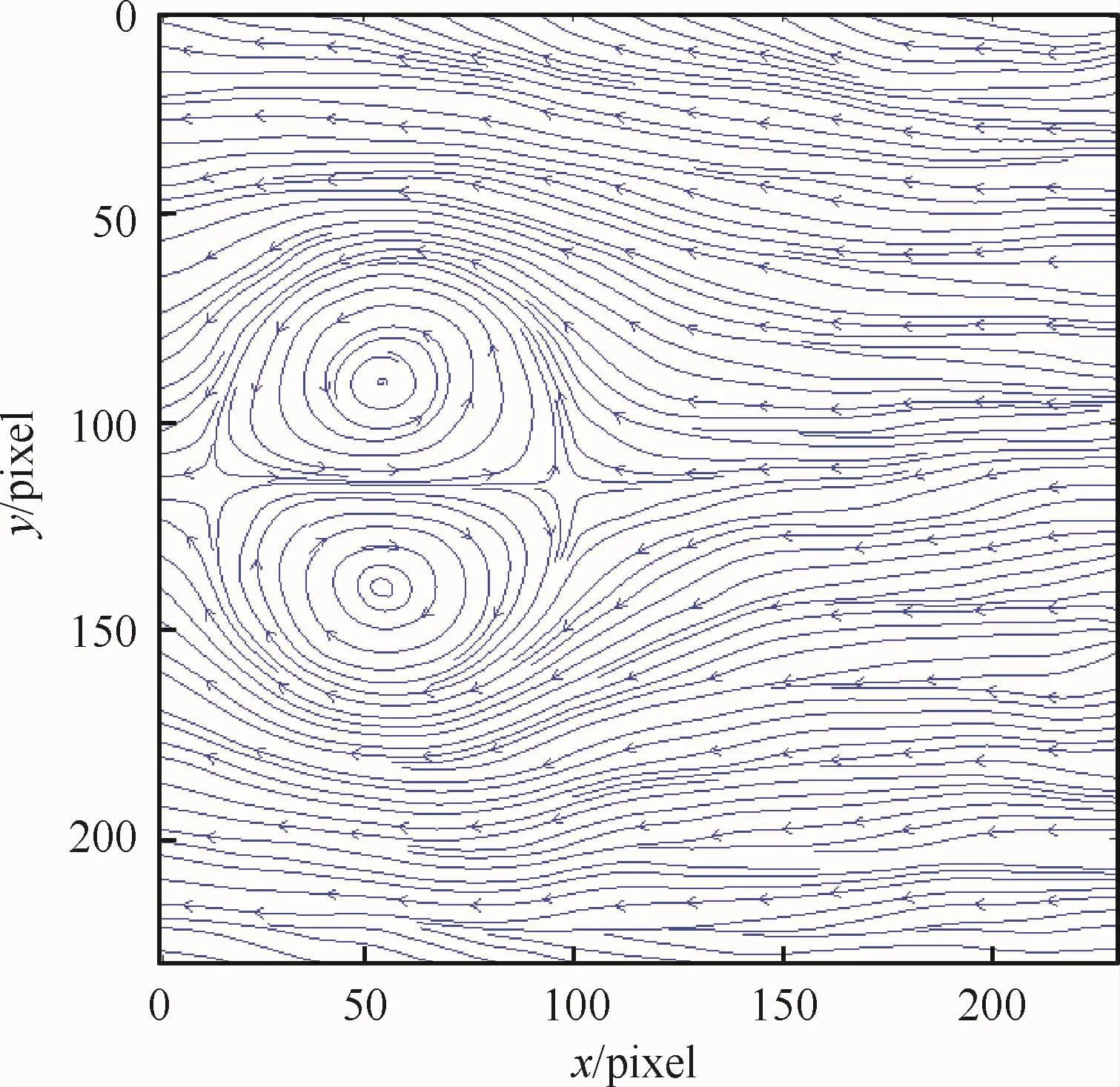
圖7 未全局平滑圖像速度流線Fig.7 Velocity streamline of no global smoothing image

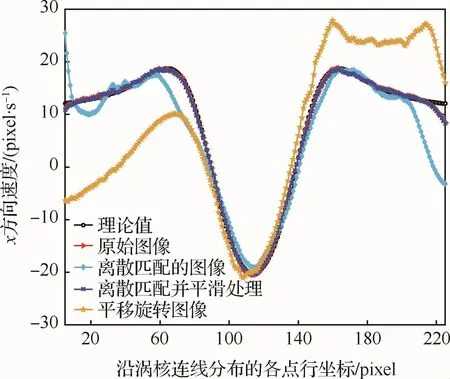
圖8 不同圖像沿Oseen渦核分布的測量速度Fig.8 Measurement velocities distributed along Oseen vortex cores for different images

表3 不同圖像沿Oseen渦核分布的最大速度相對誤差Table 3 Maximum velocity relative errors distributed along Oseen vortex cores for different images

3 風洞試驗

3.1 空腔熒光油膜路徑運動速度測量

文獻［37］給出了前緣直板擾流對高速空腔的降噪效果分析結果，鑒于文中有很好的油流試驗結果，為此，本文按照文獻［37］試驗參數，在中國空氣動力研究與發展中心（CARDC）開展了空腔熒光油膜路徑運動速度測量試驗，以對比說明本文方法的優勢。

空腔風洞試驗模型如圖9所示，模型長深比為6；模型前緣裝有直板，控制參數為：展度e＝3.3，傾角θ＝45°，底縫開度h＝1.5mm；試驗馬赫數Ma分別為2.0（2m超聲速風洞）與0.9（2.4m跨聲速風洞）；相機分辨率為4 096pixel×3 072pixel，曝光時間為1ms，鏡頭焦距為35mm。

圖10（a）、圖10（b）為2m超聲速風洞中采集的連續兩幀基準狀態下的熒光油膜圖像，對其直接利用光流法求解，得到的速度場流線如圖10（c）所示；通過圖像匹配技術對相鄰幀模型上兩個標記點A、B進行匹配，得到A點質心坐標在相鄰幀圖像上分別為（1 003，3 853）pixel、（992，3 854）pixel，B點質心坐標分別為（1 849，3 787）pixel、（1 837，3 785）pixel，表明模型振動方向主要為豎直方向。可以看出：在風洞試驗中采集的圖像，其光流求解速度方向（圖10（c））與模型振動方向一致，而與油膜實際流動方向（由空腔后緣流向前緣）不符，表明測得的速度主要反映的是模型振動，即高速風洞試驗模型的振動對熒光油膜路徑運動速度的光流求解影響巨大。

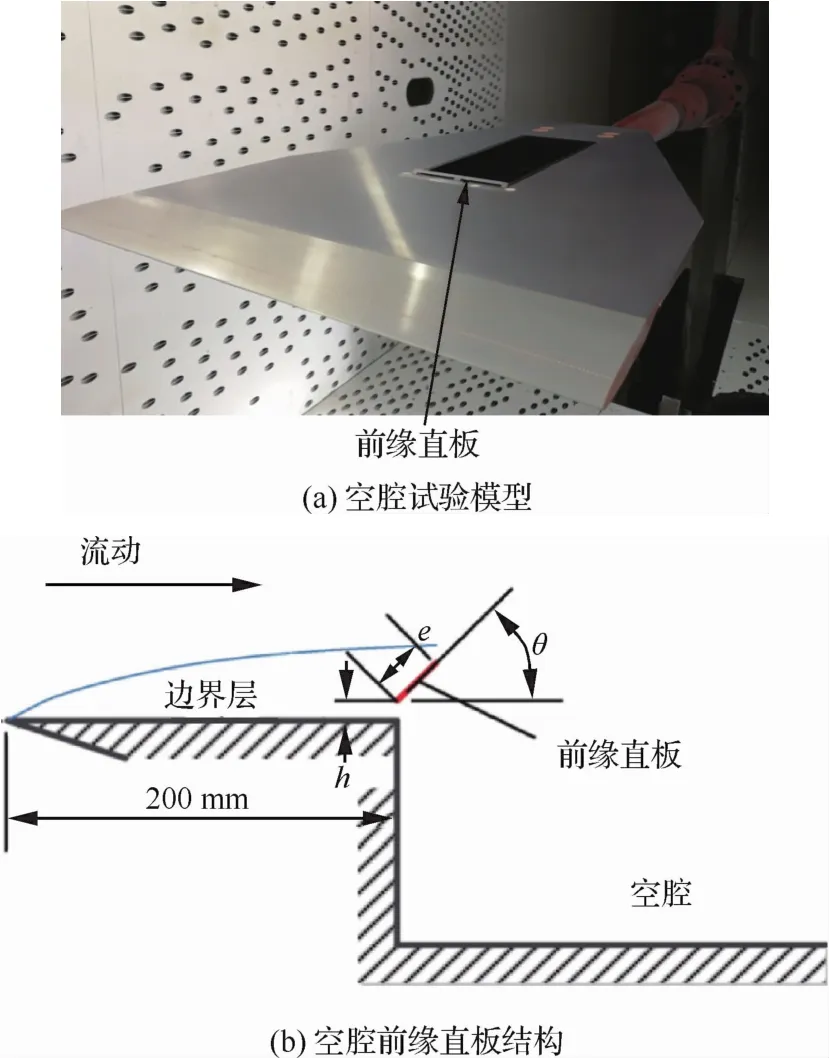
圖9 試驗模型及空腔前緣直板結構（長深比為6）Fig.9 Cavity test model and plate structure at leading edge（length to depth ratio is 6）

本文利用空腔邊界、空腔內部板面連接處邊界線（圖10（a））以及空腔模型上的紋理作為基準，利用本文算法，用式（4）得到相鄰幀圖像的映射矩陣、用式（13）得到全局平滑優化映射矩陣，在圖像空間實現模型運動與油膜路徑運動解耦，隨后經光流法求解得到油膜運動速度場，代入熒光油膜摩阻測量模型［27－30］，得到空腔壁面摩擦應力線。

在Ma＝0.9，2.0時分別采集熒光油膜運動時序圖像，通過本文離散匹配、光流法求解得到油膜路徑運動速度場，代入熒光油膜摩阻測量模型［27－30］得到摩擦應力線分布如圖11和圖12所示。

為了便于與文獻［37］中的油流結果對比，參照無量綱靜壓分布曲線呈明顯的3段式擬線性分布，本文將空腔內流場沿流向分為3個區域，Ⅰ區域x／L ∈ （0，0.43），Ⅱ區域x／L∈ （0.43，0.85），Ⅲ區域x／L∈ （0.85，1.00）。

根據摩擦應力線分布情況可知，流體撞擊空腔后緣后，沿底面回流，其中回流A沿底面中軸線向前運動，直至Ⅰ區域的分離線，其流動軌跡集中在底面中軸線及其兩側；回流B沿兩側壁流向前緣，在Ⅰ區域中撞擊前壁后改變其流向，向底面中軸線匯聚的同時轉為沿流向流動。

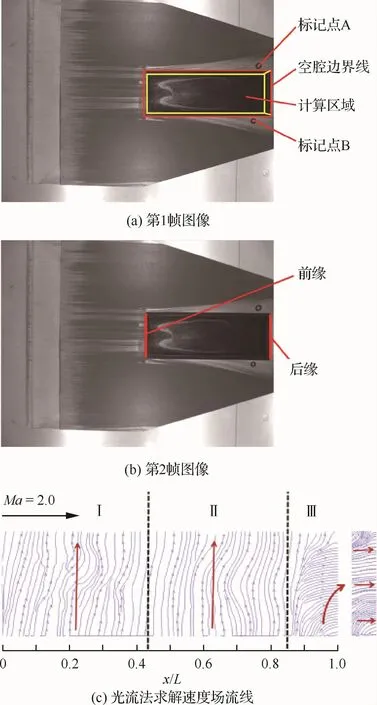
圖10 基準狀態下（Ma＝2.0）相鄰幀油膜運動圖像及其光流求解速度場流線Fig.10 Adjacent frame oil film movement images and velocity streamline by optical-flow under basic condition（Ma＝2.0）

Ma＝0.9時，回流A、B在Ⅰ區域相撞并發生流動分離。圖11（a）基準狀態下可以看出兩者交匯形成的鞍點、分離線以及沿中軸線對稱的兩個旋渦分離點；圖11（b）直板流動控制狀態下，Ⅰ區域中從后緣進入腔內的流量減少，導致回流A的強度顯著下降，因而鞍點與分離線向右移動。

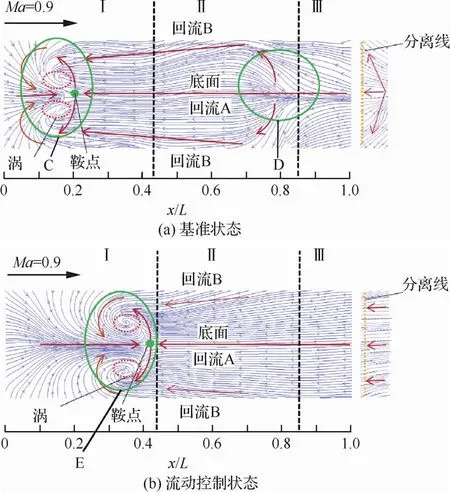
圖11 2.4m跨聲速風洞中Ma＝0.9時基準狀態和直板流動控制條件下空腔壁面摩擦應力線Fig.11 Friction stress line on cavity surfaces under basic condition and plate flow control condition at Ma＝0.9in 2.4mtransonic wind tunnel

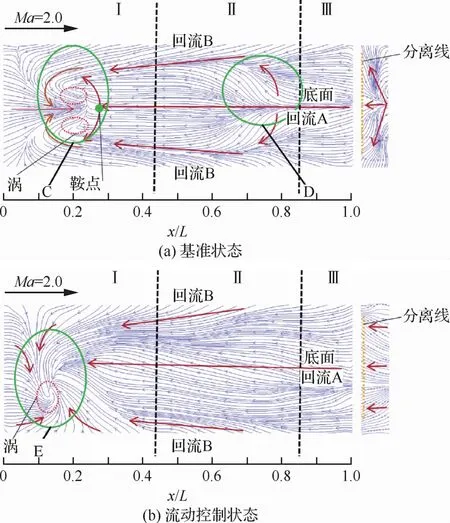
圖12 2m超聲速風洞中Ma＝2.0時基準狀態和直板流動控制條件下空腔壁面摩擦應力線Fig.12 Friction stress line on cavity surfaces under basic condition and plate flow control condition at Ma＝2.0in 2msupersonic wind tunnel

Ma＝2.0時，圖12（a）基準狀態下其流動現象與Ma＝0.9時基準狀態下類似，即回流A與回流B在Ⅰ區域相撞并發生流動分離，形成兩部分回流交匯的鞍點、分離線以及沿中軸線對稱的兩個旋渦分離點；圖12（b）直板流動控制狀態下，Ⅰ區域中沿中軸線對稱的分離線與兩個旋渦分離點被一個旋渦分離點取代，回流A、B共同匯入該分離點，使得底面摩擦應力線表現出一定的非對稱性。由于Ma＝2.0時來流的非穩定性較強，而前緣直板進一步放大了流動的非穩定性，使得腔內兩側回流B的流動失衡，因此在撞擊前壁后，匯聚過程中偏離了中軸線，形成一個距離前壁較近的旋渦分離點。

對比圖11、圖12摩擦應力線分布與文獻［37］的油流圖譜發現：在振動環境中采集的熒光油膜路徑運動時序圖像，利用本文算法對模型運動與油膜路徑運動解耦后，經光流法求解的油膜路徑運動速度場，代入熒光油膜全局摩阻測量模型［27－30］得到的摩擦應力線與傳統油流圖譜宏觀結果一致；同時，本文得到的摩擦應力線在復雜流動區域，如Ⅰ區域回流A、B交匯處（見圖11、圖12的C、E區域）以及Ⅱ區域回流A、B分離處（見圖11、圖12的D區域），提供了較傳統油流圖譜更加清晰、豐富的流動細節。表明：本文算法不僅在圖像空間實現了模型運動與油膜路徑運動的正確解耦，而且提供了更為清晰、豐富的摩擦應力線圖譜。

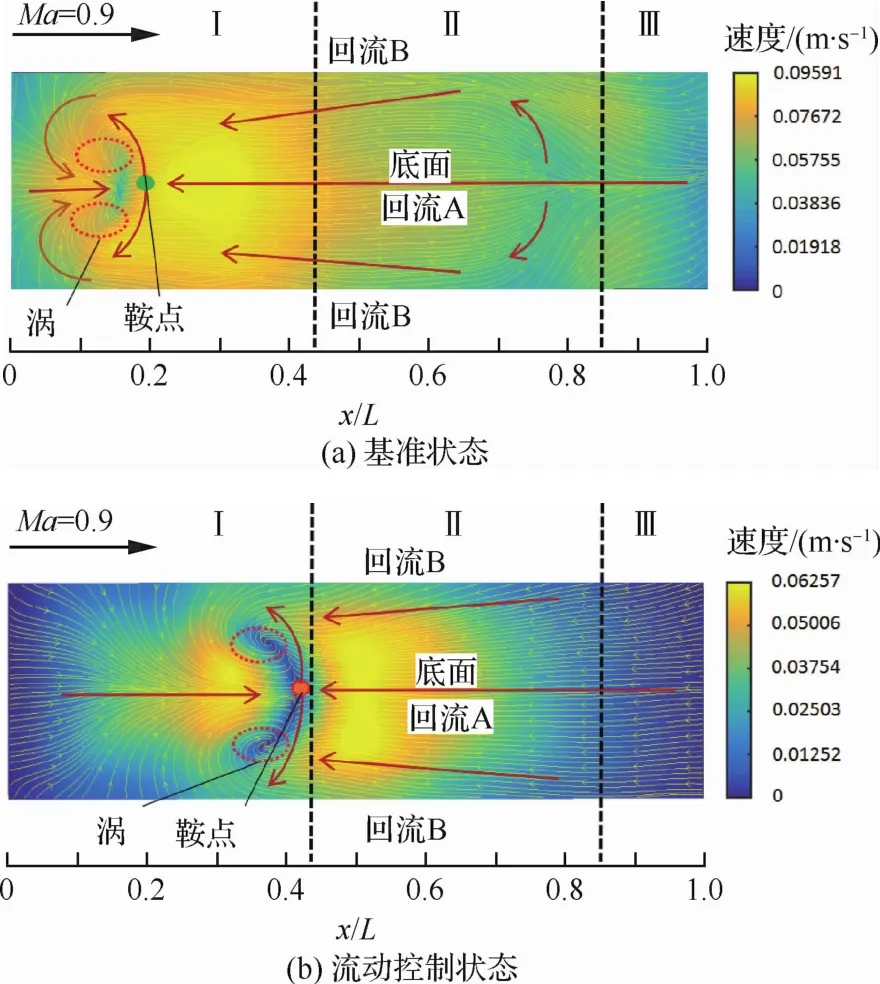
圖13 2.4m跨聲速風洞中Ma＝0.9時基準狀態和直板流動控制條件下油膜路徑速度Fig.13 Oil film path velocity under basic condition and plate flow control condition at Ma＝0.9in 2.4m transonic wind tunnel

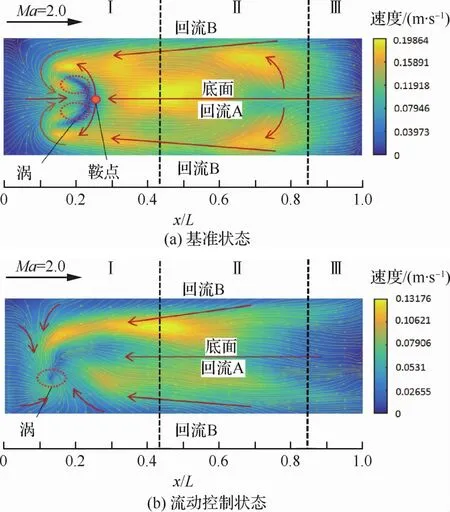
圖14 2m超聲速風洞中Ma＝2.0時基準狀態和直板流動控制條件下油膜路徑速度Fig.14 Oil film path velocity under basic condition and plate flow control condition at Ma＝2.0in 2m supersonic wind tunnel

圖13 與圖14分別給出了Ma＝0.9和Ma＝2.0時基準狀態和直板流動控制狀態下，腔內底面的油膜路徑運動光流法求解速度場，圖中顏色表示速度的大小，通過視頻測量技術［31－36］可得到速度的標準單位（m／s）。Ma＝0.9時在控制狀態下，從后緣進入腔體的流量減少，導致回流強度顯著下降，油膜流動速度相對于基準狀態出現明顯下降，達0.033 34m／s；Ma＝2.0時在控制狀態下，油膜流動速度相對于基準狀態也出現明顯下降，達0.066 88m／s。

與傳統油流結果［37］相比，本文方法不僅提供了更為清晰、準確的空腔底面摩擦應力線圖譜，而且提供了定量的油膜路徑運動速度場，為邊界層研究提供了新的手段。

3.2 某機翼表面熒光油膜路徑運動速度測量

為了驗證本文算法能夠在曲面的試驗模型上正常工作，以某大展弦比靜彈性試驗機翼為對象，在2.4m跨聲速風洞中開展驗證試驗。試驗采集圖像如圖15所示（Ma＝0.82，迎角為α＝10°）。

本文求解得到的油膜運動速度場如圖16（a）所示，代入熒光油膜摩阻測量模型［27－30］，得到機翼表面摩擦應力線如圖16（b）所示。通過對比油流試驗圖像（圖15）與機翼表面摩擦應力線圖譜（圖16（b）），發現在F、G區域油流流動分離處，油流試驗圖像上流動細節不清晰，而本文得到的摩擦應力線提供了豐富、清晰的油流流動細節。該試驗表明：本文方法同樣適用于曲面的試驗模型，得到的摩擦應力線與傳統油流圖譜宏觀結果一致，并能提供更清晰、全面的摩擦應力線圖譜。

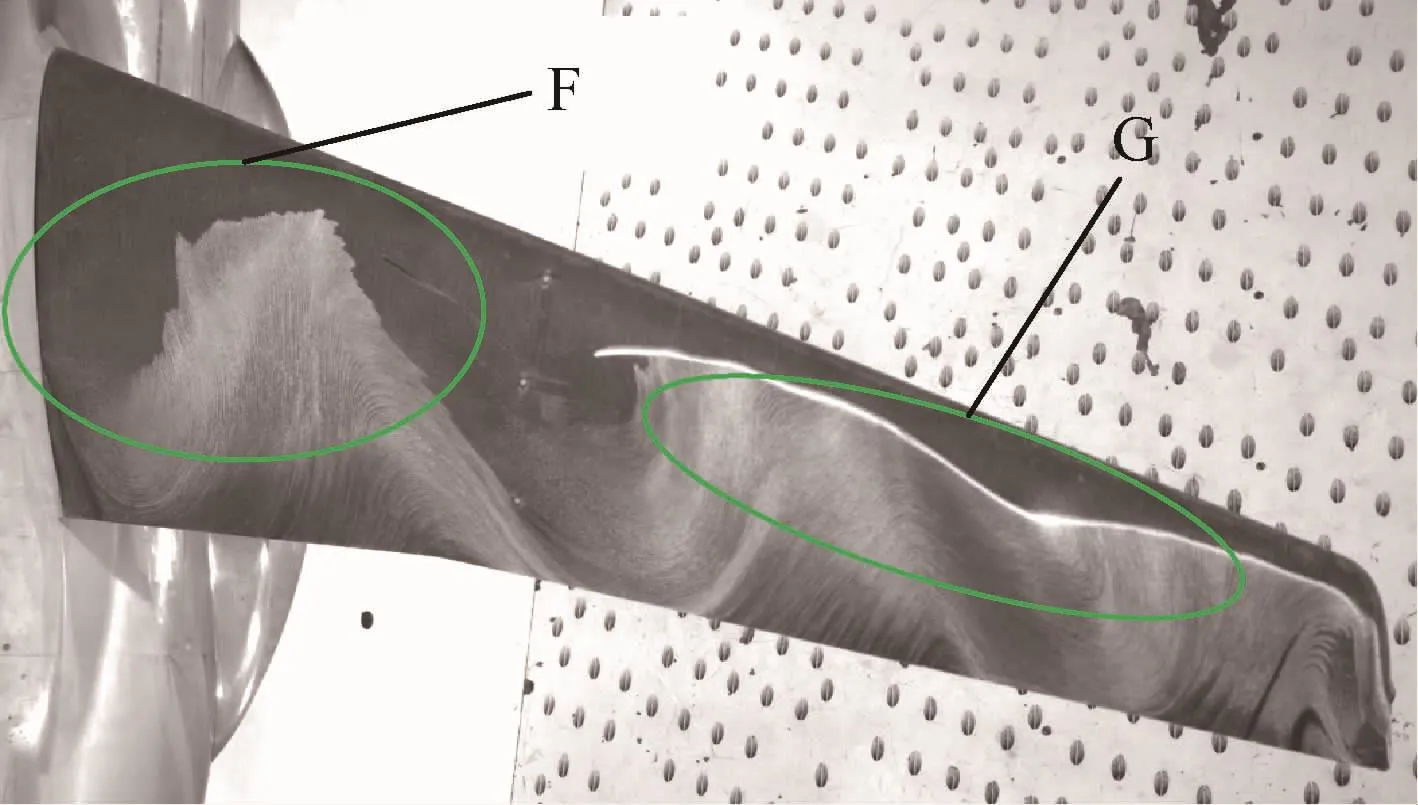
圖15 機翼表面油流試驗結果Fig.15 Test result of oil flow on wing surface

4 結 論

本文提出試驗模型表面熒光油膜路徑運動速度測量方法，通過圖像相關法離散匹配獲得相鄰時序圖像中背景紋理的（幾何位姿）映射矩陣，并推導了映射矩陣的全局平滑優化方程，實現了模型振動與其表面熒光油膜路徑運動的解耦。

1）Oseen渦對的熒光油膜路徑運動速度場仿真試驗結果表明：在給定的平移旋轉條件下，本文方法的計算結果（沿Oseen渦核連線分布的測量速度）與理論結果的最大相對誤差為4.1%，較無平移旋轉條件下的光流計算結果最大相對誤差僅增加0.6%。

2）2m量級高速風洞的空腔與機翼熒光油膜路徑運動速度測量結果進一步顯示：在空腔與機翼模型表面進行熒光油膜路徑運動速度測量試驗，不僅測得的流動現象正確，而且能得到定量的、清晰的油膜路徑運動速度場，將其代入熒光油膜摩阻測量模型［27－30］，即可獲得摩阻。模型表面摩擦應力線圖譜提供了更豐富的熒光油膜流動細節，較傳統方法優勢明顯，工程應用價值大。