鐵路曲線實測正矢轉化坐標計算的研究

廖顯軍

（南寧局集團有限公司南昆鐵路南百段增建二線工程建設指揮部 工程師 廣西 南寧 530000）

傳統的繩正法整正曲線原理是漸伸線法，但漸伸線法存在的缺陷是多方面的[1]，利用缺陷的理論整正曲線，撥量大，精度差，質量無法得到提高。而坐標法具有計算精確高、理論嚴密的優點，如何將坐標法原理應用到繩正法整正中，是工務工作者的努力方向，本文對此進行如下研究。

1 實則正矢換算現場坐標計算

根據實測正矢和弦長的幾何關系，建立統一坐標系，求對應各樁點的相對坐標，按相鄰弦線的偏角、各弦的方位角和測點坐標增量和各測點坐標幾個計算步驟如下：

1.1 首先計算各相鄰弦線的偏角 以曲線始端切線方向上的0#樁作為坐標原點，0#～1#樁連線作為橫軸建立獨立坐標系（見圖1）。

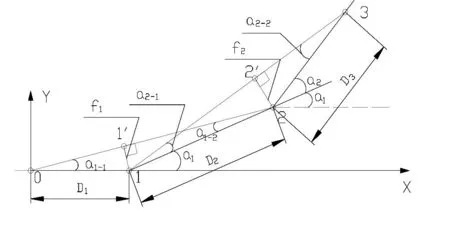
圖1 獨立坐標系示意圖

圖1中D1、D2、D3、Dn為各測點實測間距，通常為5或10m，f1、f2、fn為各測點實測正矢（不等弦長為矢距），α1、α2、α3……αn為各相鄰弦的夾角。

由圖1可知，在三角形△102中，根據三角形△外角等于兩內角之和原理，

依次類推，α2=α2-1+α2-2、……αn=αn-1+αn，以直角三角形直角邊和斜邊反求內角，公式如下：

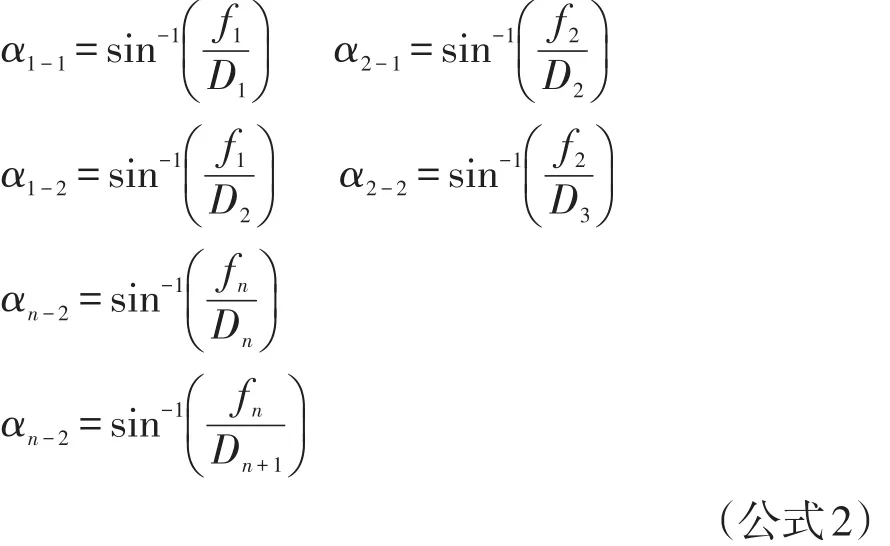
根據（公式1）和（公式2）可以計算出各相鄰弦的夾角。

1.2 計算各段弦的方位角和測點坐標增量

1.2.1 各段弦的方位角 根據圖1，弦0-1的方位角Fα0=0，1-2弦的方位角Fα1=α0+α1，

2-3弦的方位角Fα3=α1+α2，………終切線的方位角，中間各弦方位角公式為

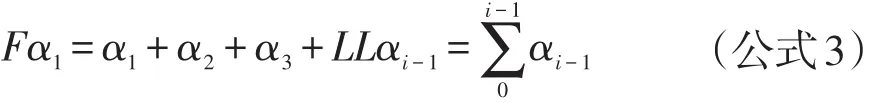
1.2.2 相鄰各測點坐標增量計算 在獨立坐標系中，某樁坐標增量=某弦方位角×某弦長，0#樁為坐標原點，其橫、縱坐標均為0，即X0=0，Y0=0

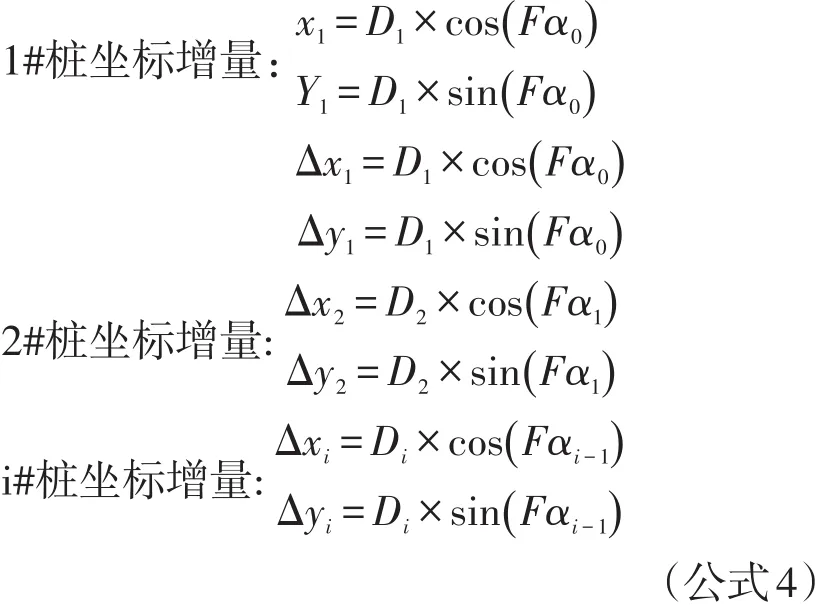
1.2.3 各測點坐標計算 圖2為獨立坐標系二示意圖。由圖1和圖2可知，獨立坐標系中某測點坐標值等于前各測點坐標增量累計（見公式5）。

圖2 獨立坐標系二示意圖

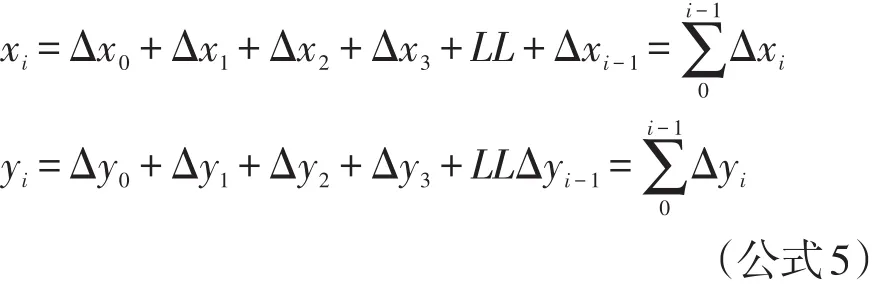
2 計算實例

根據吳耀庭著作的例子[2]，進行實測正矢轉換坐標計算，其結果如下：

2.1 各相鄰弦線的偏角

由：

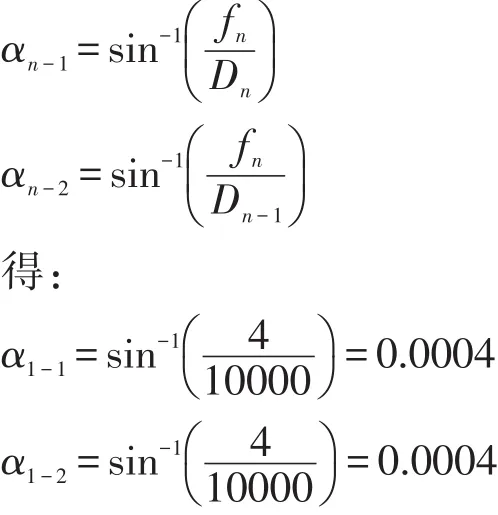
2.2 計算各段弦的方位角和測點坐標增量 以第1、2、3根弦方位角計算為例，計算方法如下：

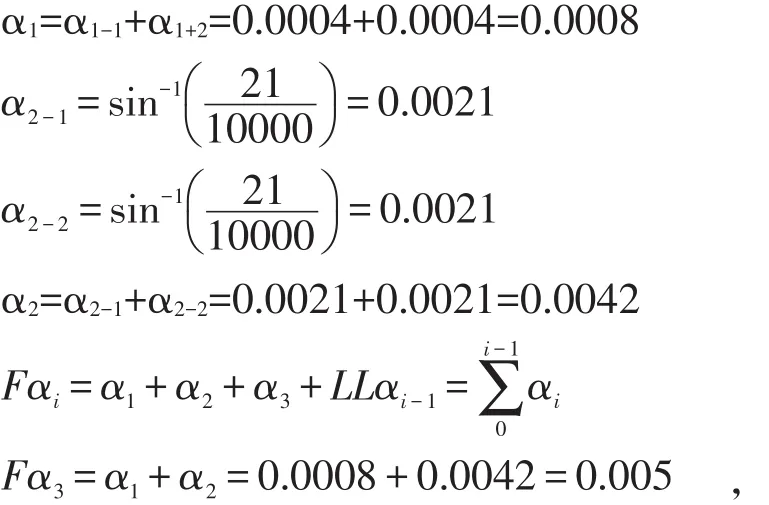
其他弦的方位角依次類推，計算結果如下表1。

表1-1 弦線方位角計算表

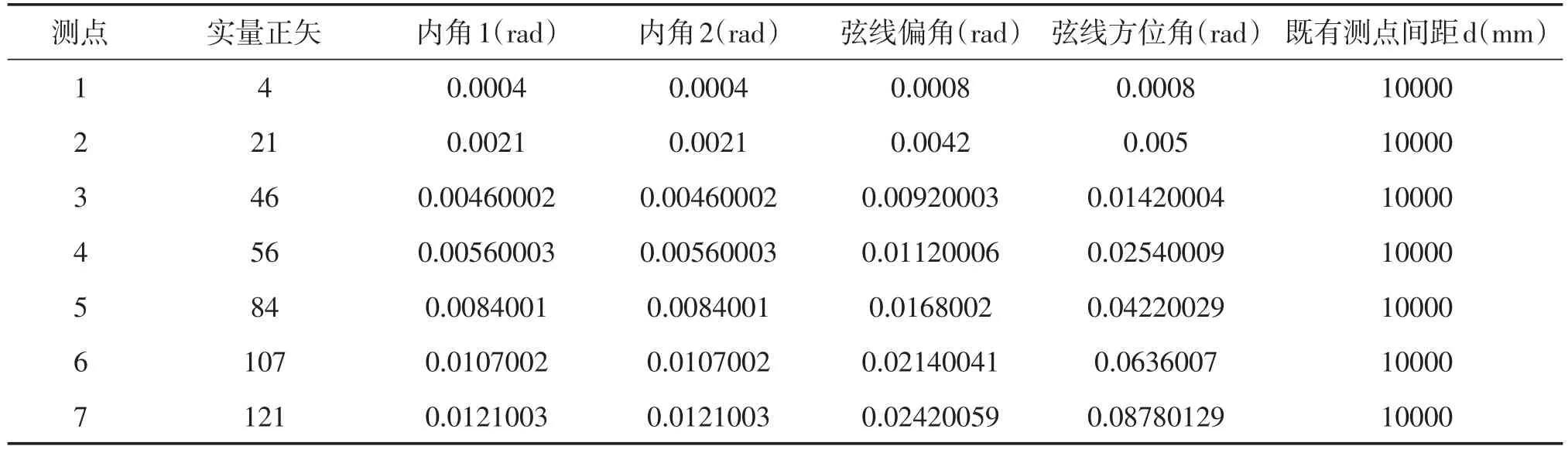
表1-2 弦線方位角計算表

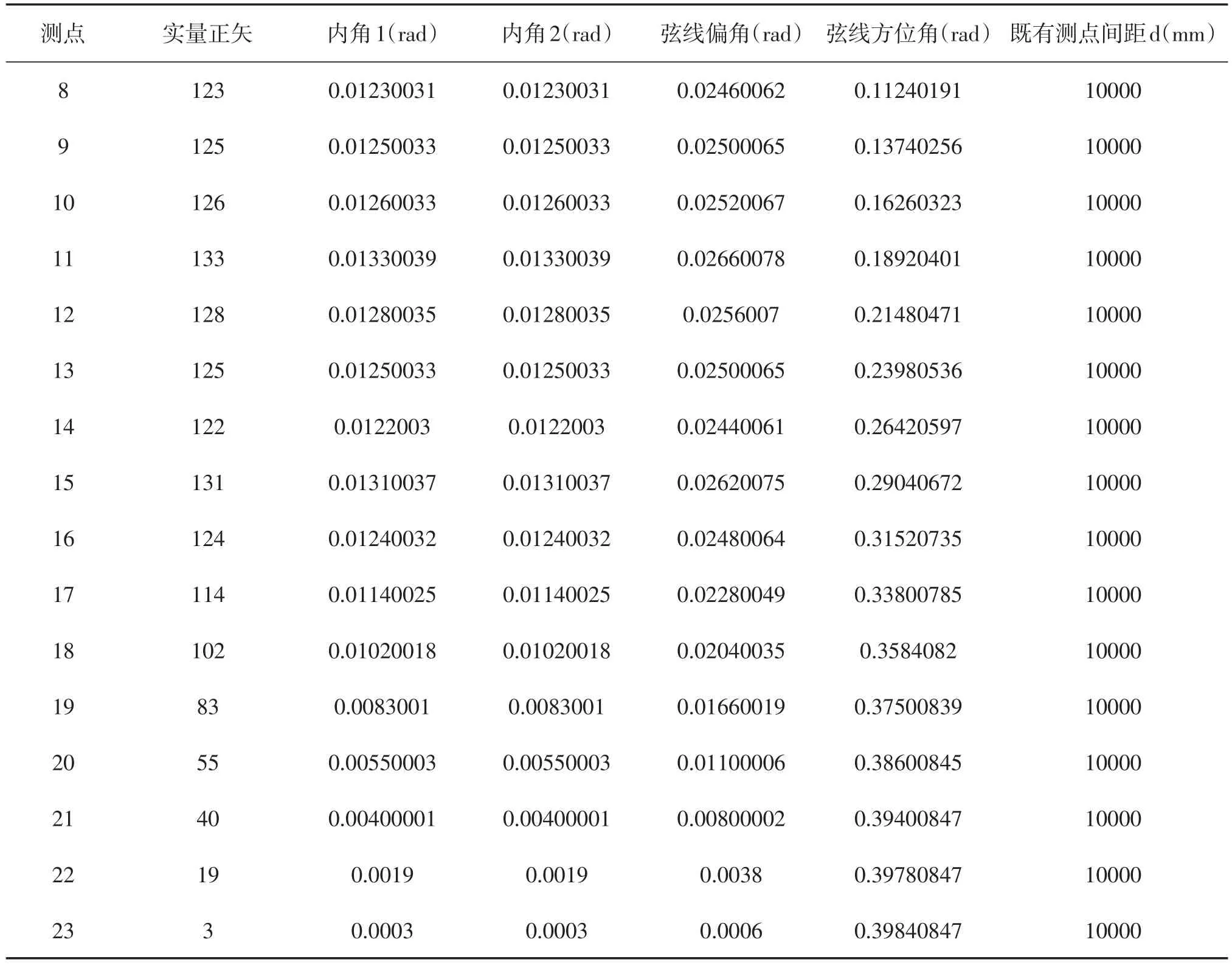
表1-2 弦線方位角計算表

2.3 各測點坐標計算 計算結果如下表，第6、7列分別為轉換的曲線實測坐標，因利用計算機程序計算，保留多位小數點：

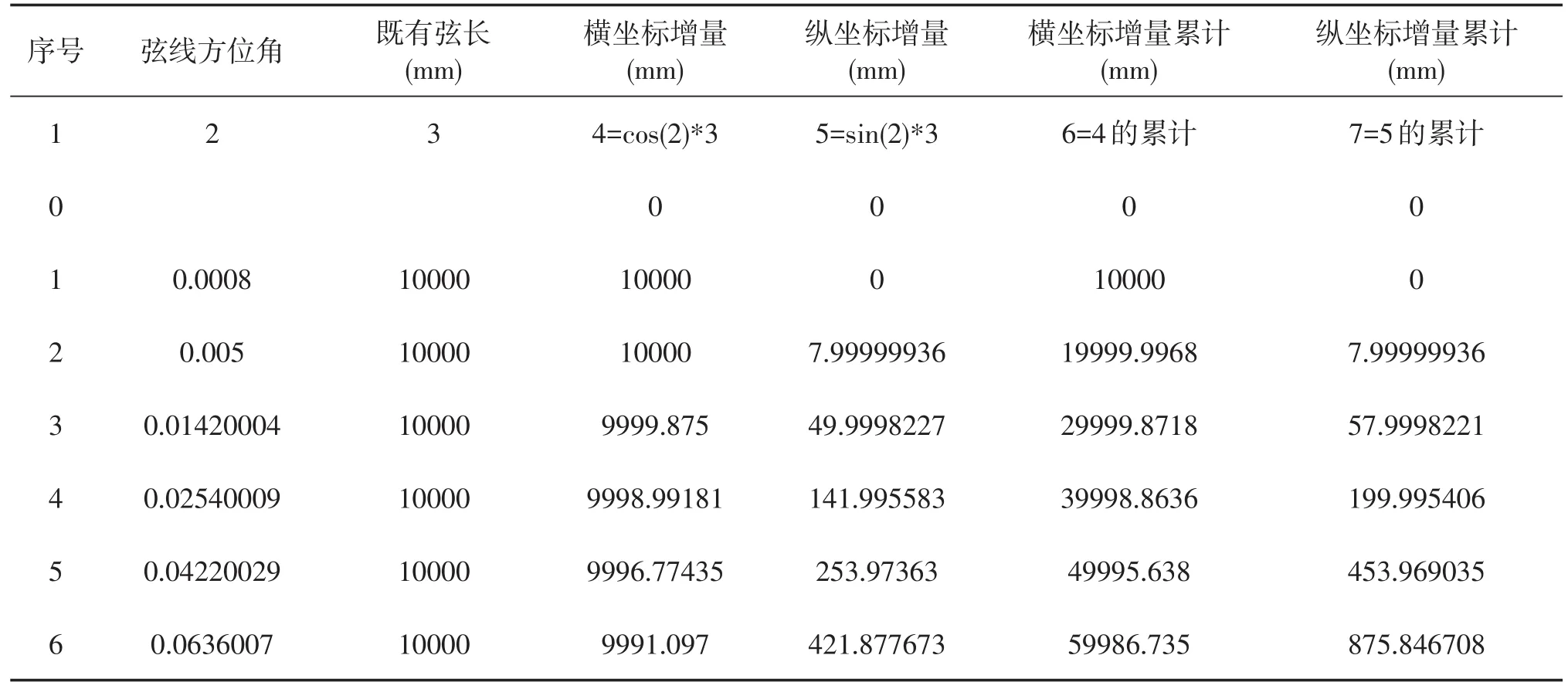
表2-1 測點坐標計算表

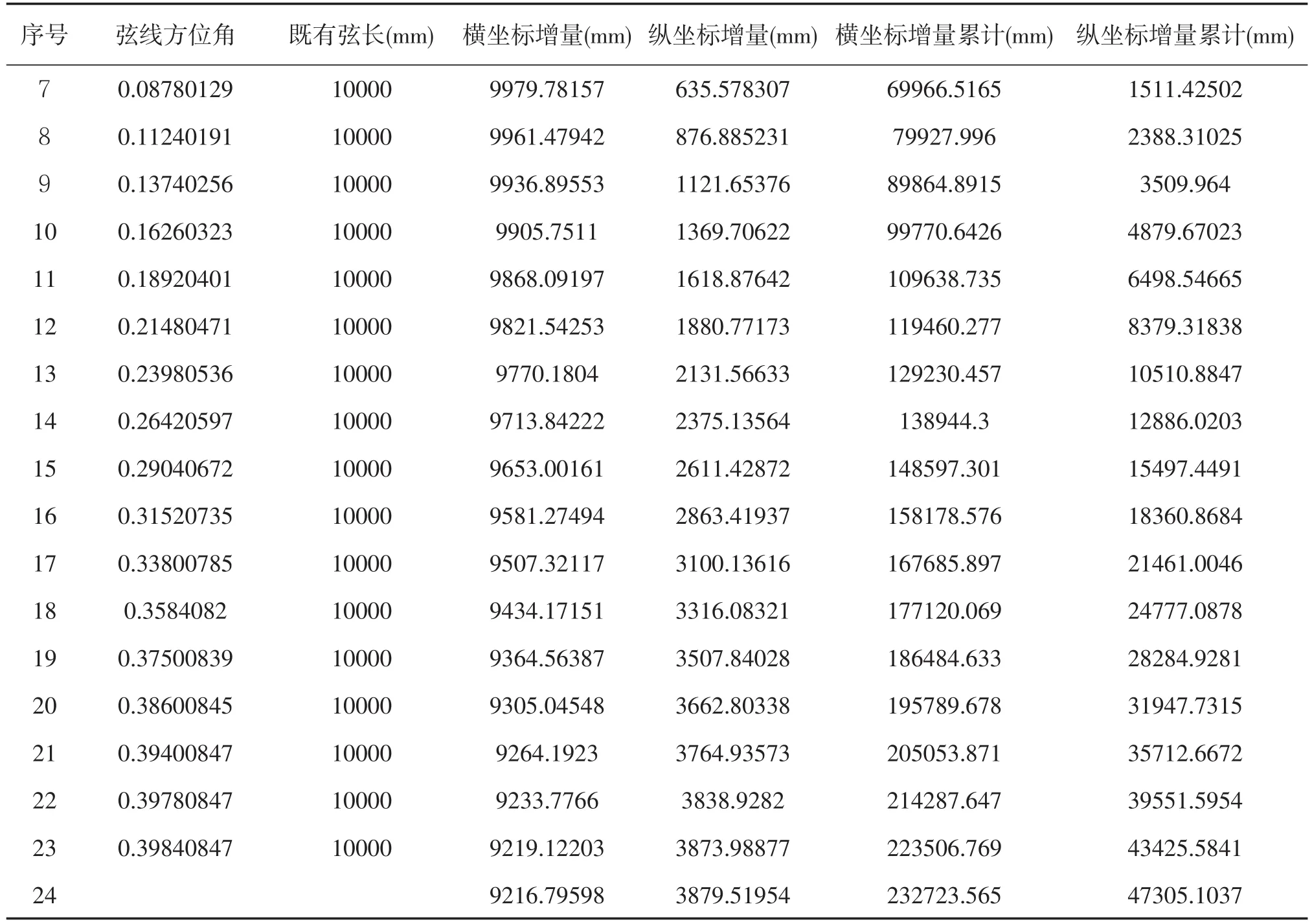
表2-2 測點坐標計算表

根據表2計算的坐標值，利用坐標法原理進行曲線整正計算，結果明顯比用傳統的繩正法漸伸線原理質量好，整正計算成果這里從略。

3 結束語

通過將實測正矢轉化為坐標，運用坐標法原理進行曲線要素優化，經過對多條曲線整正，精度高，質量好，探索出一種繩正法整正曲線的新方法，結束了繩正法只能用傳統的漸伸線理論進行整正的歷史。雖然該方法計算過程較復雜，隨著計算機的普遍應用，復雜計算可編寫計算程序解決。