壓縮載荷下織構對冷軋和退火Cu板力學行為各向異性的影響

王仁可，陳志永，邵建波，肖柱，劉楚明，唐建國

(中南大學 材料科學與工程學院，湖南 長沙，410083)

對高速沖擊下金屬材料動態行為進行研究對于金屬材料在國防和工業中應用具有重要的意義。軍事上的穿甲、爆破和工業上的高速切削、爆炸成型等均與材料在沖擊載荷、高應變率下的響應密切相關，為此，必須深入研究材料在高應變率下的動態行為。由于Cu具有良好的塑性，其已經成為高應變率下研究較多的材料[1-5]。MEYERS等[6]發現具有不同晶粒尺寸多晶Cu的動態力學行為與準靜態時的類似；NEMAT- NASSER等[7]基于位錯動力學和熱力學預測了多晶Cu的流變應力；ALEXANDER等[8]發現初始各向同性的純銅在等徑角擠壓后會出現力學行為的各向異性；LI等[9-10]研究了低溫動態塑性變形條件下Cu的微觀結構演變以及退火對納米銅動態力學性能的影響，認為高密度的變形孿生在納米晶形成過程中具有重要作用，并認為退火后納米銅的強度與延性均比應變誘導的超細晶銅的高。MISHRA等[11]研究了動態加載條件下等徑角擠壓銅的力學行為，但沒有考慮材料的各向異性。陳志永等[12]研究了冷軋Cu 板法向、軋向和橫向等軋制樣品在這3 個特征方向的動態壓縮力學行為各向異性，但對退火Cu 板展現出來的近似各向同性未進行深入研究，沒有分析織構對其行為的影響。TANG等[13-14]研究了動態變形中不同應變條件下退火Cu 板剪切帶內微觀結構的演化。MA等[15]研究了鋅含量對銅-鋅合金靜態及動態力學性能的影響。MAO等[16]分別在低/高應變速率下研究了銅應變速率敏感性與晶粒粒度的關系。作為制備銅藥型罩所需的重要原材料，初始Cu 板板平面各方向上力學行為的差異即各向異性對其破甲性能具有重要影響，其實質是織構對射流的形成和穩定性的影響。理想藥型罩應具有高密度和足夠的動態延性，且其力學行為具有近似各向同性。因此，研究織構對Cu 板力學行為各向異性的影響有重要意義，且具有重要的實際應用價值。為此，本文作者利用 Instron 電子拉伸機和分離式Hopkinson 壓桿等實驗裝置，研究準靜態和動態壓縮條件下織構多晶冷軋和退火Cu 板板平面力學行為各向異性特征規律，考慮晶體學取向分布即織構并基于微觀晶體塑性理論，探討織構對其力學行為各向異性的影響規律，以期為金屬材料動態力學行為的研究以及高性能破甲彈的研制提供參考。

1 實驗

以工業純Cu為原料，原始狀態為鍛態，初始厚度為60 mm，冷軋變形總壓下量90%至6 mm，截取部分冷軋板材在450℃退火2 h。對冷軋和退火Cu板分別沿與板材軋向成0°，45°和90°方向取圓柱形試樣(樣品編號分別為RD-0°，RD-45°和RD-90°)，其長度和直徑均為5 m，然后，在Instron 電子拉伸機和分離式霍普金生壓桿(split hopkinson pressure bar,SHPB)實驗裝置上進行準靜態(應變率約為1×10-3s-1)和動態(應變率約為4×10-3s-1)壓縮實驗，并獲得不同方向上的準靜態和動態壓縮應力-應變曲線。采用全自動X線衍射儀測量樣品{111}，{220}，{200}和{113}不完整極圖，應用BUNGE[17]球函數諧分析法及LüCKE[18]高斯函數織構組分擬合方法計算相應的取向分布函數ODF(orientation distribution function，最大展開項級數lmax=3，包括偶數項和奇數項展開系數)。

2 結果

2.1 退火Cu 板織構

圖1所示為冷軋變形和相應退火后Cu 板的真ODF圖。從圖1(a)可以看出：冷軋Cu 板取向分布具有軋制變形織構基本特征，主要聚集在取向空間α和β 線附近；α 線上主要有高斯取向G{110}〈001〉(0°，45°，0°)和黃銅取向B{110}〈112〉(35°，45°，0°)，在此取向線上所有取向的{110}面平行于板平面；β 線由銅取向 C{112}〈111〉(90°，35°，45°)經由S{123}〈634〉(61°，34°，64°)(具體位置略有變動)與α 線相交于黃銅取向B。圖1(b)所示為退火Cu 板的真ODF，從圖1(b)可以看出其同時具有軋制變形織構和再結晶退火織構特征，軋制織構主要為C 織構，再結晶織構主要為立方織構，可見在此情況下其再結晶過程尚未充分完成。

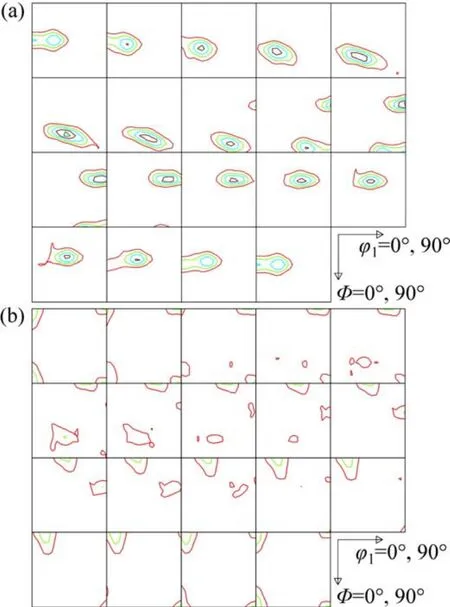
圖1 冷軋和退火Cu 板的真ODF圖Fig.1 True ODFs for cold-rolled and annealed copper sheets

2.2 織構多晶體板材壓縮力學行為各向異性

圖2所示為冷軋織構多晶Cu 板各方向的壓縮真應力－真應變曲線。在加載過程中，各個試樣都經歷了明顯的彈性變形與塑性變形階段。從圖2(a)可見：在準靜態壓縮變形時，RD-90°樣品的屈服強度和流變應力最大，RD-45°樣品次之，RD-0°樣品最小；在高應變較高時，各樣品的流變應力變化趨勢趨于一致。從圖2(b)可見：動態壓縮變形時，依然是RD-90°樣品屈服強度和流變應力最大，RD-45°樣品次之，RD-0°樣品最小。以上結果表明無論是準靜態還是動態壓縮變形，冷軋織構多晶Cu 板的力學行為均具有明顯的各向異性，且變化規律一致，在動態加載下，各向異性更加顯著。圖3所示為退火Cu 板不同方向上的準靜態壓縮應力-應變曲線。從圖3可見：不同方向上的屈服強度以及在真應變低于0.2 時的流變應力基本一致，力學行為近似各向同性；當真應變高于0.2 時，各方向上的流變應力略微有所差別。盡管準靜態下退火Cu 板壓縮力學行為表現出的各向異性程度很小，但織構分析表明退火Cu 板的晶體取向分布表現出一定程度的擇優取向，故需分析織構對冷軋和退火板材平面不同方向的壓縮力學行為的影響規律。

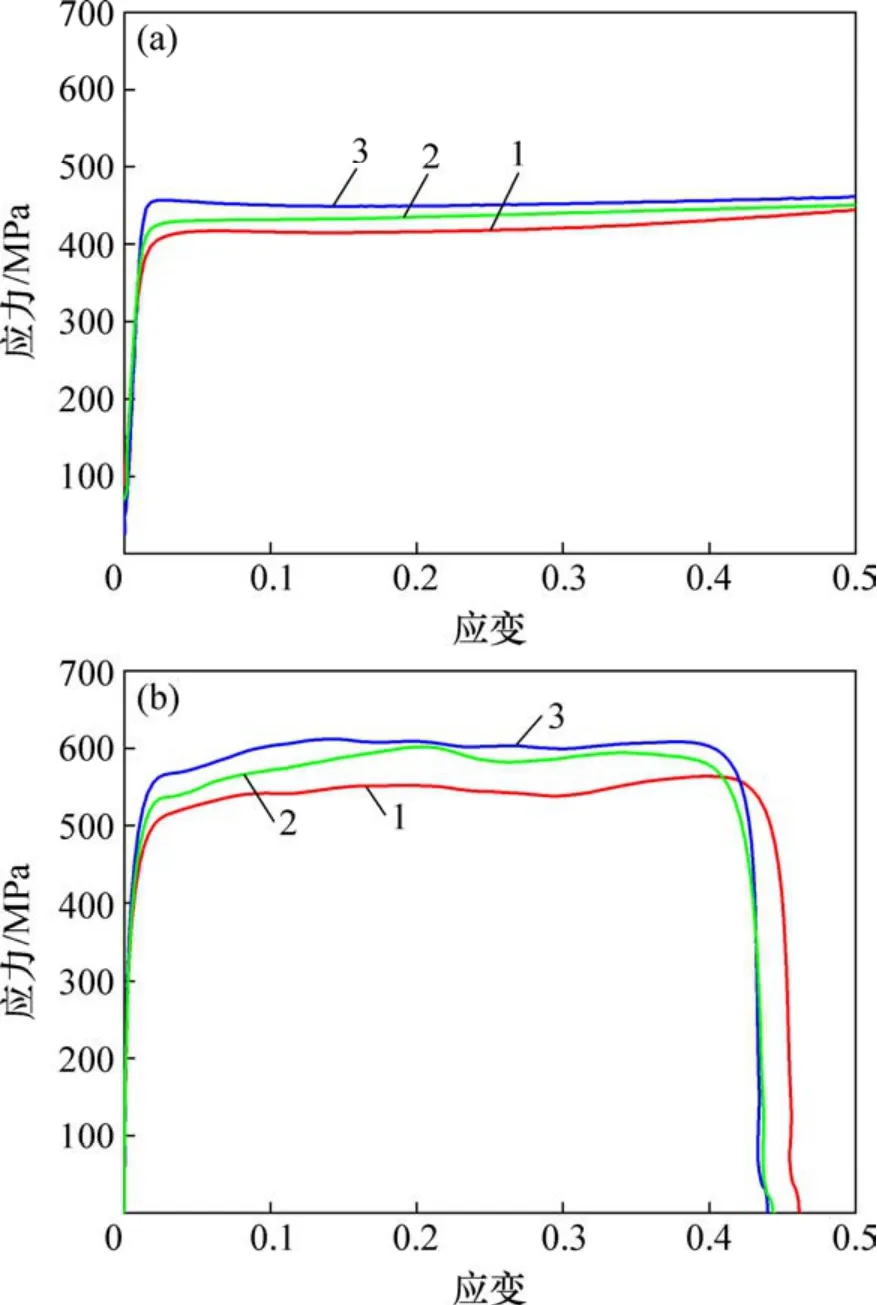
圖2 冷軋Cu 板準靜態和動態壓縮真應力-真應變曲線Fig.2 Compress true stress-strain curves of samples with different directions for cold-rolled copper sheet

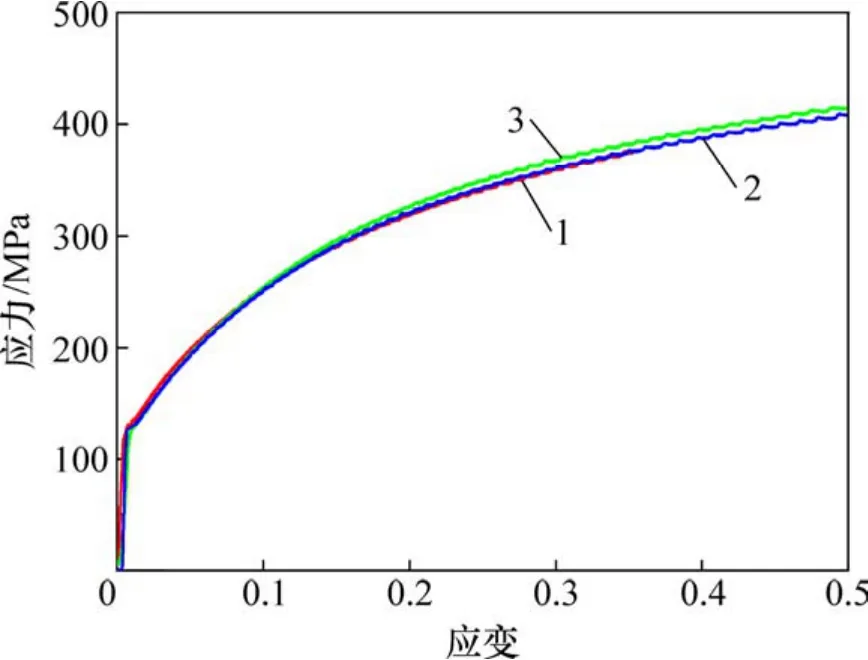
圖3 退火Cu 板準靜態壓縮(應變率約為1×10-3 s-1)真應力-應變曲線Fig.3 Quasi-static compressive(ε˙is about 1×10-3 s-1)true stress-strain curves of samples with different directions for annealed copper sheet

3 分析與討論

冷軋Cu 板織構較強，其力學行為表現出各向異性。退火Cu 板盡管織構較弱，但依然表現出一定的擇優分布，其力學行為近似為各向同性，故難以依據多晶體板材內是否存在織構來判斷其是否存在各向異性。當多晶體內具有織構時，其宏觀性質受到相應單晶體的各向異性以及晶粒取向分布這2 個因素的雙重影響，在此情況下，材料的宏觀行為可以表示為晶粒微觀行為的總和。基于此，對于具有初始織構的樣品，首先將初始樣品離散化，即將其表示為一些具有特定權重分立取向的組合。圖4所示為離散化后，由具有特定權重分立取向計算的取向分布函數(ODF)，與實測ODF(見圖1)相比，離散化后的晶體取向保持了冷軋和退火Cu 板織構的基本特征，可作為其各向異性分析的出發點。

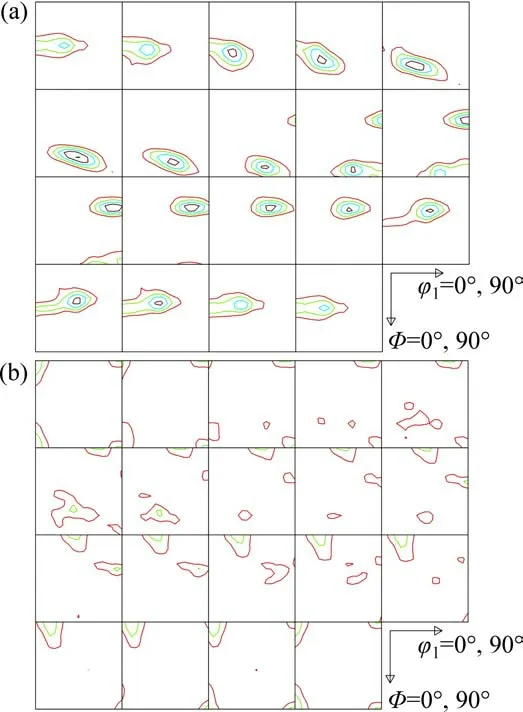
圖4 冷軋和退火Cu 板的離散化后的真ODFFig.4 True ODFs calculated from individual orientations for cold-rolled and annealed copper sheets

一般地，當單晶體的塑性行為確定后，金屬多晶體的塑性行為依賴于微觀物理量向宏觀物理量轉換，因此，考慮單個晶粒變形機制的多晶塑性理論時必須將它們聯系起來。根據塑性變形條件，人們提出了多種多晶體變形模型，主要分為 SACHS[19]和TAYLOR[20]模型以及由此而產生的各種修正模型。對于fcc 金屬，由于Taylor 模型比Sachs 模型更能反映實際結果，因此，本文采用Taylor 模型分析其壓縮行為各向異性。

為便于分析織構多晶板材不同方向上的力學行為，采用R，S和C分別表示軋制(RD，TD，ND)、樣品壓縮(X，Y，Z)和晶體(〈100〉，〈010〉，〈001〉)的坐標系。Taylor 模型假定多晶聚集體內各晶粒所承受的應變與宏觀應變一致。對于多晶聚集體壓縮塑性變形，它可由X方向上的壓縮變形以及Y和Z方向上的延伸變形來描述，應變張量可表示為

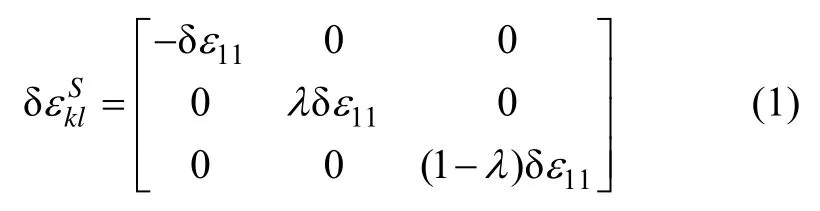
式中：上標S表示樣品壓縮坐標系。設α為壓縮方向(X)相對于軋向(R)的夾角，即樣品壓縮坐標系相對于軋制坐標系的夾角，則軋制坐標系相對于樣品壓縮坐標系的取向矩陣為

依據張量轉換法則：

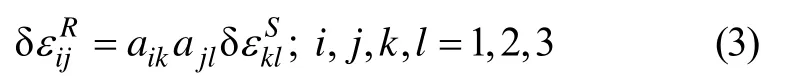
可將樣品壓縮坐標系上的應變張量轉換到軋制坐標系。假定晶體坐標系相對于軋制坐標系的取向矩陣為g，則有

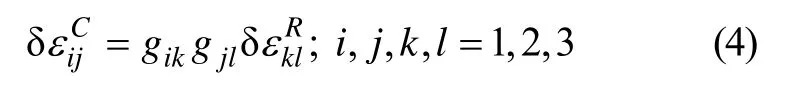
其中：

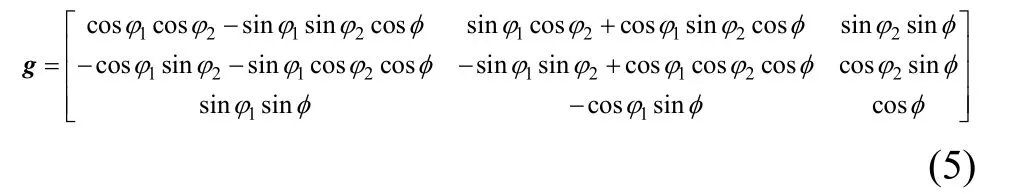
從軋制坐標系出發，將晶體坐標系按φ1，φ和φ2順序轉動，即可得到歐拉空間的任一取向(φ1，φ，φ2)。對于任意取向的晶粒，將BISHOP-HILL[21-22]最大塑性功原理拓展于滑移或/和孿生共生變形之中，根據

可以確定實際所需的屈服應力(包括滑移或/和孿生屈服應力)，由此也可確定相應啟動的滑移或/和孿生系。定義Taylor 因子為

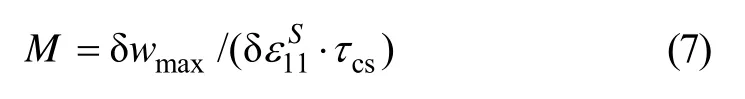
其中：csτ為{111}〈110〉滑移臨界剪切應力。在此基礎上，進一步考慮晶體取向分布，將上述過程應用于具有一定初始織構的樣品的離散化取向，再根據各自的權重Vi加權計算總的Taylor 因子，即

顯然，可以將任一取向的Taylor 因子作為相對強度的度量：Taylor 因子越大，使材料產生塑性變形所需外力越大。

由于Cu為中等層錯能金屬，在室溫準靜態變形條件下變形機制一般為{111}〈110〉滑移；在沖擊載荷即本文實驗條件下，{111}〈110〉滑移和{111}〈112〉孿生機制可能同時發生作用。CHEN等[23]對fcc 晶體引入孿生機制，將滑移和孿生綜合起來進行考慮，系統分析了當{111}〈112〉孿生對{111}〈110〉滑移的臨界分解剪切應力之比ξ不同時，fcc 晶體滑移和/或孿生共生單晶共生屈服應力狀態及其特征，發現：當時，僅能產生滑移，有56 種應力狀態；當時，僅能產生孿生，有25 種應力狀態；只有當時，滑移和孿生才可能同時產生，且僅存在2種類型混合屈服面，其臨界值為，共有259種應力狀態，其中139 種相同，120 種不同。在此基礎上，根據各種多晶體塑性變形模型，結合織構離散化后冷軋和退火Cu 板具有一定權重的分立取向，可以計算不同塑性變形機制起作用下的織構多晶板材的Taylor 因子，分析其壓縮行為各向異性。

圖5所示為僅考慮{110}〈111〉滑移變形機制時，采用上述方法計算的冷軋和退火織構Cu 板平面內不同方向的Taylor 因子。計算時考慮了樣品對稱性，即對于某一取向g1(φ1，φ，φ2)，有3 個對稱取向g2(180°+φ1，φ，φ2)，g3(180°-φ1，180°-φ，φ2)和g3(360°-φ1，180°-φ，φ2)。很明顯，對于冷軋織構多晶Cu 板，其不同方向上的Taylor 因子差異較大：隨著軋制方向角度增大，其Taylor 因子先減小，在33°方向附近其Taylor 因子最小，然后，隨著與軋制方向角度的增大而進一步增大，在RD-90°方向上的Taylor 因子達到最大，表現出強烈的各向異性，且Taylor 因子相對于RD-90°方向對稱。對于退火織構多晶Cu 板，其Taylor 因子變化非常平緩，與初始織構為自由取向分布的各方向的Taylor 因子相差不大，近似為各向同性，說明盡管退火Cu 板晶體取向擇優分布具有初始織構，但由于其再結晶織構和形變織構達到了較好平衡，其宏觀壓縮力學性質表現出近似各向同性。

圖6所示為考慮{110}〈111〉滑移和/或{112}〈111〉孿生變形機制時和共4 種情況)計算的冷軋和退火織構Cu 板板平面內不同方向的Taylor 因子。需指出的是：隨著ξ減小，其Taylor 因子均降低，這并不意味著使金屬產生塑性變形的外力越來越低。這是因為隨著應變率增加，由于Cu為應變速率正敏感性材料，其滑移和孿生的臨界分解剪切應力也隨之增大，導致其產生塑性變形的外力也相應增大。顯然，對于冷軋織構多晶Cu 板，隨著ξ減小即塑性變形機制由滑移向滑移和/或孿生塑性變形機制轉變，其Taylor 因子的變化規律是相似的，均表現出各向異性，且各向異性程度越來越低。對于退火織構多晶Cu 板，不管其塑性變形機制如何變化，其Taylor 因子變化較平緩，近似為各向同性。將Taylor 因子歸一化，也可得到同樣結論。

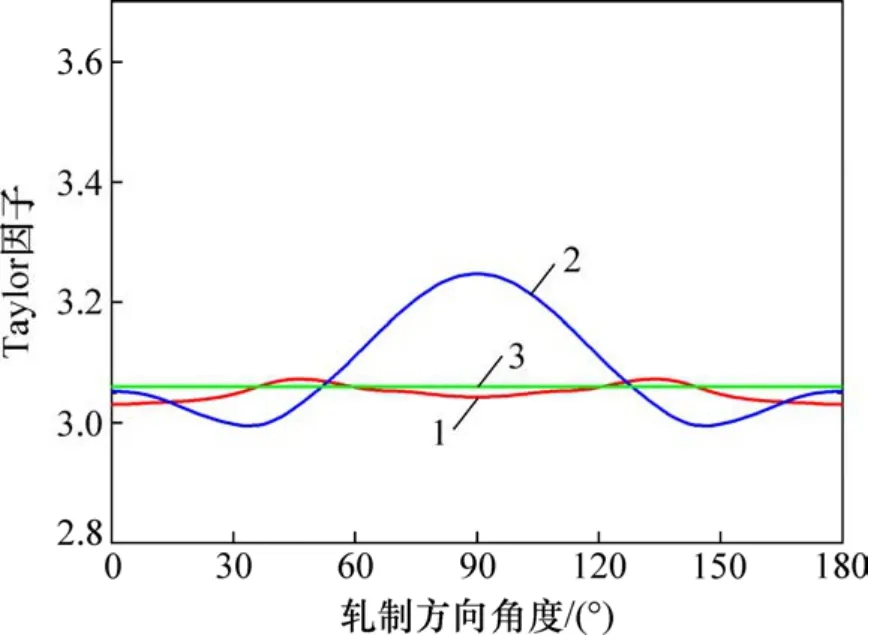
圖5 僅考慮{110}〈111〉滑移時冷軋和退火Cu 板Taylor 因子Fig.5 Taylor-factors of cold-rolled and annealed Cu sheet considering{110}〈111〉slip

圖6 考慮{110}〈111〉滑移和/或{112}＜111〉孿生時 Cu 板的Taylor 因子Fig.6 Taylor-factors of Cu sheets for{110}〈111〉slip and/or{112}〈111〉twinning

由上述分析可知：無論是準靜態還是動態壓縮變形，對于冷軋和退火織構Cu 板，考慮晶體取向分布即織構的影響，其各向異性規律與實驗結果定性符合，可見本文分析結果與實際結果基本相符。

4 結論

1)退火織構多晶Cu 板3 個方向上的力學行為差別很小，近似為各向同性；相比較而言，冷軋織構多晶Cu 板準靜態和動態壓縮力學行為呈現出明顯的各向異性，RD-90°方向屈服強度和流變應力最大，RD-45°方向的次之，RD-0°方向的最小。

2)考慮晶體取向分布即織構的影響，計算了板平面內與軋制方向成不同角度樣品方向導致壓縮塑性變形所需外力強度因子，結果可用于定性解釋織構多晶Cu 板壓縮力學行為各向異性。退火Cu 板表現出近似各向同性的原因是其再結晶織構和形變織構共同作用即兩者之間相互平衡。