基于更新Kriging模型的雙重螺旋法加工齒面的重構方法

鄧辰，嚴宏志,3，陳義忠，伊偉彬

(1.中南大學輕合金研究院，湖南長沙，410083；2.中南大學高性能復雜制造國家重點實驗室，湖南長沙，410083；3.中南大學機電工程學院，湖南長沙，410083)

與傳統的“五刀法”加工螺旋錐齒輪相比，雙重螺旋法具有高效、綠色制造的特性[1-8]。張宇等[7]對雙重螺旋法的切齒原理以及螺旋錐齒輪的動靜態嚙合性能等方面進行了研究。由于螺旋錐齒輪齒面形狀復雜，不能使用顯示函數表達。為了分析及優化螺旋錐齒輪的嚙合性能，一般基于機床調整參數仿真加工形成螺旋錐齒輪齒面。由于已有軟件仿真加工齒面精度較低，不適合作為后續動靜力學分析的模型，因此，目前大多數集中在NURBS 函數的擬合研究。其中，林家春等[9]利用數據點進行NURBS 曲面擬合，建立齒面三維參數化模型，解決了特大型齒輪特征線測量問題；ZHAN等[10-11]在NURBS 齒面重構基礎上對擬合后的曲面進行最小二乘法再次優化逼近。一些三維軟件建模都用類似的樣條曲線擬合三維曲面，但因結果受其控制點及權因子等多方面因素的影響，最終精度不理想。與多項式最小二乘法、樣條曲線等插值方法相比，Kriging 作為一種估計方差最小的無偏估計模型，具有全局近似與局部隨機誤差相結合的特點，它的有效性不依賴于隨機誤差的存在，對非線性程度較高和局部響應突變問題具有良好的擬合效果，能夠對擬合點進行誤差控制，由此Kriging 模型在近些年得到了廣泛運用。楊麗等[12]運用Kriging 模型預測了齒輪嚙合剛度，由此以齒輪動態傳動誤差響應波動最小為目標對齒輪修形參數進行了優化；CHEN等[13]將Kriging 模型與支持向量回歸結合，對受噪聲影響的數據進行了精確預測；佟操等[14]基于MonteCarlo 法，結合Kriging 預測，提出一種主動學習可靠度計算方法；陳志英等[15]將粒子群優化算法引入Kriging模型，快速準確地預測了輪盤危險點的應變變程；李小剛等[16]提出了一種雙層更新的Kriging 模型，對某型號大型汽輪發電機定子端部繞組錐環固定結構動態特性進行了穩健優化設計。MUKHOPADHYAY等[17]對比了不同Kriging 模型的精度和計算效率，研究了不同協方差函數的比較性能，然后利用隨機Kriging 法解決了噪聲在不確定傳播中的作用。本文作者以實現雙重螺旋法加工螺旋錐齒輪三維幾何精確建模為目標，通過提取適當的型值點，進行基于更新Kriging 模型的齒面重構研究，以便為雙重螺旋法螺旋錐齒輪嚙合性能準確分析提供支持。

1 雙重螺旋法齒輪加工原理

依據螺旋錐齒輪雙重螺旋法成型原理，大輪使用成形法加工，小輪使用雙重螺旋法加工。與小輪雙重螺旋法加工相比，大輪加工不附帶刀傾機構與螺旋運動機構，而且搖臺不需要在繞自身轉動的同時還要沿其軸線方向做進給運動，其大輪理論齒面方程可參考文獻[2-6]，因此，在此主要介紹小輪的雙重螺旋法加工原理。

小輪刀盤側刃切削面的其次坐標方程為

式中：rt1為刀盤名義半徑；W1為刀頂距；u1為切削刃上任意一點到刀尖的距離；α1刀具齒形角；θ1為刀盤相位角；凸面取“-”，凹面取“+”。

同理，刀盤側刃切削點處的法向量nt1與切向量tt1分別為：

式(2)中小輪輪齒凹面取“-”，凸面取“+”；式(3)中小輪輪齒凹面取“+”，凸面取“-”。

圖1所示為小輪加工坐標系σ1={O';i1,j1,k1}，其中，O'為機床中心，O1為小輪設計交叉點，Oo1為刀盤中心；i1-j1所在平面為機床平面；S1為徑向刀位，q1為角向刀位，XB1為床位，X1為軸向輪位，E1為垂直輪位，I為刀傾角，J為刀轉角，δM1為小輪輪坯安裝角。產形輪的軸向與k1軸方向相同，用單位矢量k1=[001]T表示。

小輪產形面方程位置矢量在機床坐標系的表達為：

式中：Mo1o′為刀盤坐標系到機床坐標系的坐標變換矩陣；Mdz和Mdq分別為小輪刀盤經過刀傾角和刀轉角的坐標變換矩陣；Lo1o′，Ldz和Ldq分別為Mo1o′，Mdz和Mdq的三階主子式。

而小輪交叉點O1到機床中心O′的位移矢量為

圖1 小輪加工坐標系Fig.1 Coordinate system to manufacture pinion

式(7)中床位XB1會隨著加工過程發生變化，與螺旋運動系數有關[8]。

設產形輪的角速度為1，即ωp=k1，小輪轉速為ω1=io1p1，其中，io1為加工小輪時的滾比，而小輪產形輪與工件之間的相對角速度ω與相對速度v分別為：

式中：Hl為小輪雙重螺旋法加工的一階螺旋運動系數。

最后，將小輪齒面方程表示在以小輪設計交叉點O1為原點的坐標系中，即可得到小輪的齒面方程：

2 Kriging模型及齒面重構優化方法

2.1 Kriging模型

對待求曲面基于Kriging模型進行擬合可表示為

式中：y(x)為未知的Kriging模型；x=[x1,x2,…,xi,…,xn]T，為其中一個輸入樣本，n為輸入的樣本維數，為第i維中有m個樣本點；f(x)=[f1(x),f2(x),…,fi(x),…,fp(x)]T為回歸多項式基函數向量，p為回歸多項式的數量；β=[β1,β2,…,βi,…,βp]T為多項式參數向量；z(x)為Gaussian 隨機過程函數，其期望為0，方差為σ2，協方差矩陣為

式中：xi與xj為不一樣的隨機變量；R(θ,xi,xj)有多種函數形式可以選擇，在此，選擇參數θ=[θ1,θ2,…,θi,…,θn]T的高斯函數作為相關系數，R(θ,xi,xj)表示為

式中：θk為未知的相關參數。

根據Kriging理論，在未知點x的預測值為

式中：c=c(x)=[c1(x),c2(x),…,ci(x),…,cm(x)]T，為試驗點在預測點處的響應向量，m為試驗點數。

考慮Gaussian隨機過程，為確保預測值無偏且預測均方誤差最小，采用拉格朗日乘數法求最小值，可得

式中：F為n個樣本構成的設計矩陣。將式（15）代入式（14）可得

對于回歸問題Y?Fβ，由最小二乘法可得多項式參數向量：

再將式（17）代入式（16）得

式中：r*可通過已知設計點的殘差計算得到，即Rr?=Y-Fβ?。

為了使預測值無偏差且預測均方誤差最小，在未知點x處的Kriging 預測值的均值uG(x)和方差分別為：

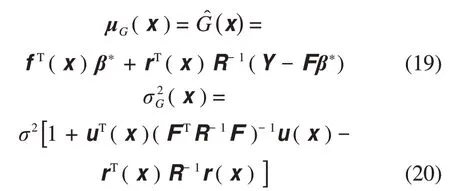
式中：u(x)=FTR-1F-f(x)具體推導過程見文獻[18]。

2.2 基于Kriging模型的齒面重構優化方法

1)采樣點的選擇。只有選擇按齒面上按一定規律分布的采樣點才能得到光滑的齒廓曲面。一般地，采樣點越多，擬合的齒面和理論齒面越接近，但是相應的計算時間也會越長。因此，在滿足精度要求的前提下，盡量使用較少的型值點進行曲面重構。齒面型值點的采集如圖2所示。以每個加工仿真齒面上齒高、齒長方向的N×M個數據點作為初始采樣的型值點進行齒面擬合。

2)數據歸一化處理。對型值點的數據進行歸一化，即

圖2 齒面型值點的采集Fig.2 Extraction of initial data points on tooth surface

式中：xi,nomalized為歸一化后的第i維樣本；i=1,2,…,m；k=1,2,…,n;xi,min=min(xi)為型值點在第i維上的最小值；di=max(xi)- min(xi)為第i維上的m個數據點之間的最大距離。型值點歸一化后再建立Kriging模型，可提高其精度和魯棒性[19]。

3)擬合精度判斷。基于Kriging模型的更新策略，用復相關系數R2作為全局精度的檢驗標準，其值越接近1，則模型的全局近似精度越高。

同時，以最大絕對誤差為局部近似精度檢驗標準，其值越接近0，則模型的局部精度越高。

最大絕對誤差Emax為

均方根誤差ERMSE為

平均絕對誤差Emean為

這些參數也作為檢驗曲面擬合精度的判據。首先，基于Kriging 模型求出控制頂點的數據，再對擬合曲線的R2進行判斷，若R2滿足預定要求，則保留模型，輸出控制頂點；否則，對模型進行更新。具體方法為：若求出控制頂點中最大絕對誤差小于0.001 mm的點，則將這些數據作為新增樣本加入初始樣本點集中，以此加密樣本從而提高局部精度；否則，將求出的控制頂點中最小值的點作為新增樣本加入初始樣本點集。再以新樣本點集為基礎繼續進行歸一化處理，然后重新進行新的Kriging 擬合，直至R2滿足預定要求為止。

4)進行蒙皮操作。根據上一步所得的控制頂點，采用蒙皮法生成重構的齒面。

整個齒面重構流程如圖3所示。

圖3 齒面重構流程圖Fig.3 Flow chart of reconstructing tooth surface

3 算例

以1對螺旋錐齒輪為例，其基本參數與機床調整參數如表1和表2所示。基于不同數目的型值點進行基于更新Kriging模型的曲面重構，并將其與在Pro/E中通過樣條曲線擬合的齒輪模型進行對比，得到重構齒面誤差特征值如表3所示。

由表3可得：通過樣條曲線擬合出的Pro/E 模型重構齒面平均絕對誤差為采用本文更新Kriging 模型的3.294 9×106倍。基于更新Kriging 模型重構螺旋錐齒輪齒面精度更高。

采用差曲面表達建模的誤差可更直觀反映重構精度。取法向偏差作為Kriging 模型誤差可得其差曲面如圖4和圖5所示。

從圖4和圖5可知：用基于更新的Kriging方法得到的擬合結果中，最大誤差為1.539 0×10-6μm，最小誤差為-3.348 4×10-7μm，擬合齒面點基本與理論齒面點坐標一致；而通過Pro/E生成的齒面，其最大誤差為11.833 8 μm，最小誤差為-16.443 4 μm。由此說明采用本文更新Kriging 模型擬合齒面更接近理論齒面。

表1 齒輪基本參數Table 1 Basic parameters of gear and pinion

表2 齒輪機床調整參數Table 2 Machine Setting Parameters of gear and pinion

表3 不同重構數據比較Table 3 Comparison of reconstructing data for different models

圖4 Kriging模型差曲面圖Fig.4 Ease-off of Kriging model

圖5 Pro/E模型差曲面圖Fig.5 Ease-off of Pro/E model

4 結論

1)基于更新Kriging 模型，通過采樣點選擇、型值點歸一化、Kriging 模型的更新策略、蒙面法提出了齒面精確重構優化方法。

2)與常用樣條曲線擬合方法相比，本文重構方法所建模型更接近理論齒面，誤差更小，精度更高，為后續的齒面接觸分析(TCA)以及承載齒面分析(LTCA)提供更為可靠的模型基礎。