考慮渦流效應的磁懸浮轉子非線性振動分析

劉學平，朱戡

(清華大學深圳研究生院 先進制造學部，廣東 深圳 518000)

磁懸浮軸承(Active Magnetic Bearing，AMB)可以提供非接觸式支承力，調節剛度和阻尼，具有無機械摩擦力,轉速高,溫升小等優點。由于電磁軸承中電磁力的非線性，往往需要將其線性化以便于控制。文獻[1]最早提出線性化模型，利用一對差動電磁鐵構造出近似的線性力-電流模型。為了避免該模型局部線性化的問題，其他線性化方法也被陸續提出[2-3]。

磁泄漏、裂紋轉子、轉子與定子的碰摩運動都會導致非線性響應。在磁場分析方面，文獻[4]研究了在軸向電磁軸承中，隨著氣隙間距的變化磁泄漏對電磁力的影響。在轉子的碰摩分析方面，文獻[5]研究了磁懸浮軸承中轉子與保護軸承接觸的各個方面，并且介紹了相關的控制方法。

傳統文化中隱藏著中華精神和靈魂。隨著國學的普及和發展，傳統文化的價值日益被現代中國人所接受和認可。語文教學中滲透傳統文化，可以提升學生的道德品質和民族自豪感，有助于身心的修養和完善，并幫助學生樹立中國人特有的認識世界和理解世界的觀念，做一名熱愛祖國熱愛人民的好學生。

在電磁力所引發的非線性問題上，文獻[6]考察了在非線性電磁力作用下，幾何耦合參數對磁軸承柔性轉子運動的影響，發現當參數較大時系統存在明顯的分岔、次同步諧振等非線性現象。文獻[7]對磁懸浮軸承的分岔行為進行了分析，并用Lyapunov第一定理分析了系統的穩定性，發現系統中存在廣泛的分岔、跳躍、多值響應和較大的初值敏感性。文獻[8]考察了磁懸浮支承柔性轉子的非線性振動，研究了轉子的連續性和電磁力的非線性，發現了非線性模態下的內共振現象。文獻[9-10]分析了在不同參數激勵下擁有時變剛度的電磁軸承的動力學響應，考察了轉子的響應情況，發現轉子非線性響應較豐富。文獻[11]利用多尺度方法計算了具有時變剛度的磁懸浮軸承的瞬態和穩態響應。文獻[12]考察了存在轉子角度偏移的電磁軸承的非線性動力學響應，發現隨著幾何參數的變化，系統產生了大量的次同步諧振、準周期和混沌現象。文獻[13]考察了存在時變剛度和幾何耦合的磁懸浮軸承，并且利用非線性PD控制推遲了分岔發生的時間點，提高了轉子的響應性能。

目前的研究大多集中在電磁力固有非線性導致的軸承剛度及阻尼非線性對磁軸承行為的影響，較少關注渦流產生的非線性對磁軸承的影響。因此，現考慮渦流效應對電磁力的影響，建立磁懸浮轉子的動力學模型，分析轉子的頻率響應。

1 磁懸浮轉子模型

1.1 考慮渦流的電磁力模型

磁懸浮軸承原理如圖1所示。圖中：u為電磁鐵的端電壓;i為電磁鐵線圈電流;a,b分別為鐵芯寬度和厚度的一半;l為磁路長度;s為氣隙總長度。

新零售不再受空間時間束縛，去邊界化特征。新零售的興起打破了傳統零售業基于時間和空間的經營邏輯，不斷被削弱營業時間、經營范圍、業態區域等對消費者的控制力，消費品受品種、數量、形態的限制也越來越低，消費體驗和商品交換活動逐漸呈現出無邊界性。

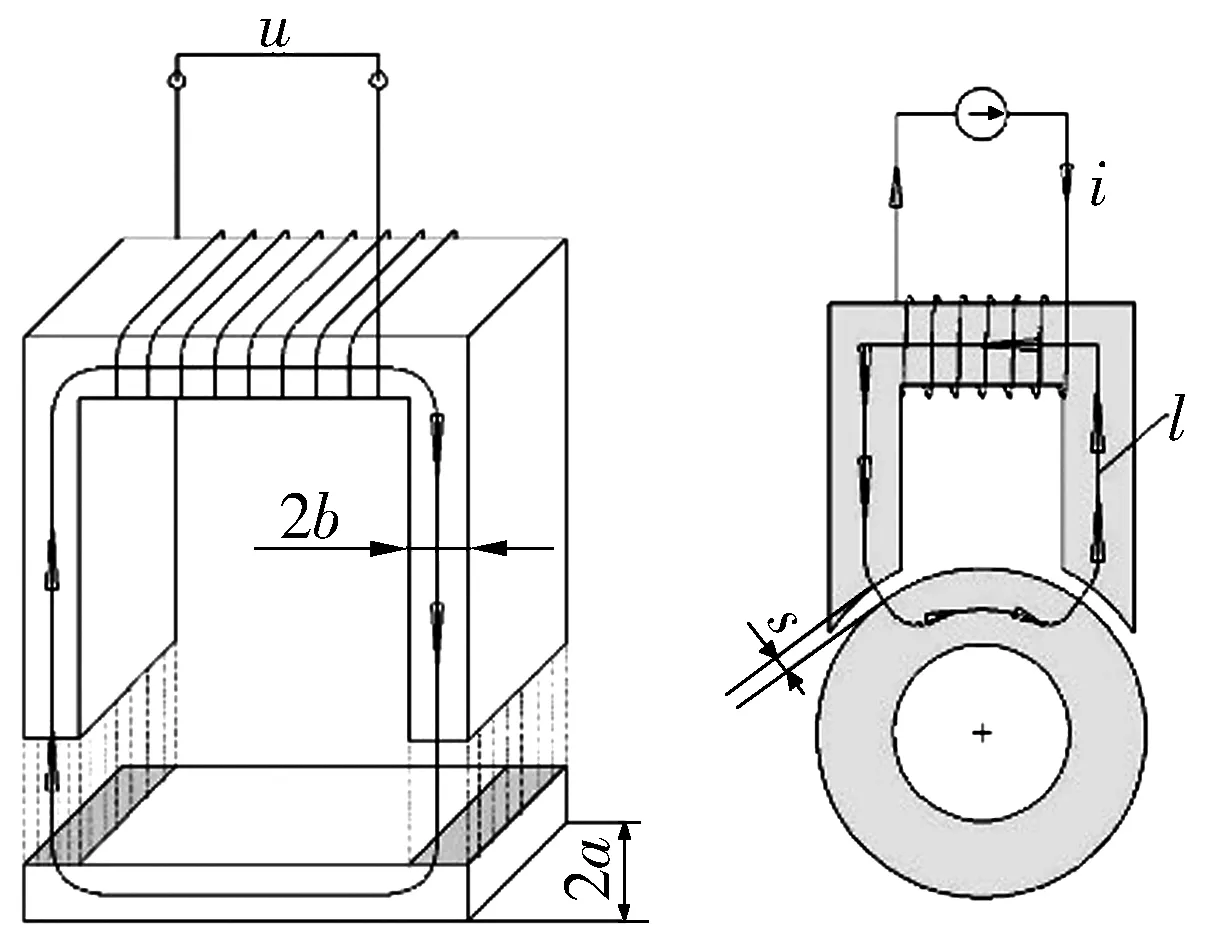
圖1 磁懸浮軸承原理圖

當電流按照正弦規律變化時，其產生的磁場強度H滿足

(1)

式中：σ，μ分別為鐵芯的電導率和磁導率。利用Laplace變換，設H=H0esjt，sj為Laplace變量，則(1)式變為

(2)

磁感應強度B與磁場強度H之間的關系為

B=μH，

(3)

由此可得磁感應強度空間分布為

(4)

式中：B0為鐵芯中心處的磁感應強度。

磁通量φ與磁感應強度的關系為

φ=B0A，

(5)

由此可得

(6)

式中：A為鐵芯的橫截面積,A=4ab。

利用磁路法，可知磁感應強度B0和線圈匝數N、電流i、磁路總長度l(x)滿足如下關系

(7)

式中：s(x)為氣隙總長度；μ0為真空磁導率；μr為鐵磁導率，μr?1；lfe為鐵芯氣路長度。

將以上參數代入原方程，并聯合(14)～(17)式，經化簡可得

(7)式可化簡為

(8)

結合(6)，(8)式，系統的磁通量與線圈電流滿足以下頻域關系

(9)

將(9)式進行級數展開，并保留主要的一次項，可得

本文的KBE系統集成技術包括知識集成和系統集成。KBE系統與之前的傳統專家系統相比在產品設計時更加偏重于知識集成，可以實現在產品設計過程中，充分調動和利用各種知識資源；系統集成方式將KBE系統集成到CAD系統，增加KBE系統的功能，使其變得更加完善。NX系統為KBE系統提供了一個可視化環境，能夠利用面向對象語言對設計的三維模型進行建立和修改，利用數據庫和電子表格來存儲知識信息，以及編輯Dfa文件實現知識的傳遞和規則庫的建立。本文為了方便實現知識的集成，采用統一數據庫，不需要知識數據的轉換，將知識管理系統集成到NX系統中，實現知識庫中數據的添加、刪除和更新以及KF模塊知識的獲取。

(10)

(10)式即磁通量與線圈電流在頻域中的關系式,為了便于分析，將其轉換為時域表達式

(11)

由此可知，除了電流項以外，磁通量還與電流的微分項有關。

通常電磁軸承中采用差動模式，作用在轉子上的電磁力可以表示為位移和電流的函數[1]4，即

紙漿洗滌過程并非一個穩態的模型就能準確地辨識，要用一個動態變化的模型逼近紙漿洗滌過程，前述研究中采用了神經網絡的兩步辨識法得到紙漿洗滌模型。兩步辨識法：①采集大量的動態數據為樣本，訓練多輸入的神經網絡，通過訓練好的神經網絡辨識動態生產過程；②以此動態神經網絡生成的大量樣本數據為穩態模型的樣本，訓練只有主導輸入的穩態模型，訓練好的神經網絡可穩定模擬生產過程的穩態特性。

(12)

式中：x為轉子位移。

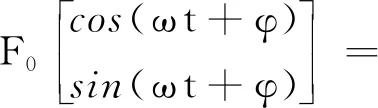
圖1中磁懸浮軸承的電磁力為

(13)

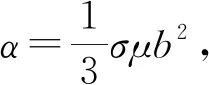
(14)

1.2 轉子動力學模型

轉子的動力學模型為

(15)

式中：x，y為轉子的徑向位移;轉子受力除了重力mg(g=9.8 m/s2)外，還包括轉子質量不平衡所導致的不平衡力Fw和電磁鐵施加的電磁力Fs。

細菌培養基：稱量牛肉膏1.5 g、蛋白胨3.0 g、NaCl 1.5 g、瓊脂6.0 g，再加入清水300 mL煮沸，調節pH7.0。

(16)

式中：F0為轉子所受偏心力；md為轉子的不平衡質量；ω為轉子轉速；e為轉子偏心量；φ為初始相位角。

當采用比例-微分(PD)控制時，需要建立關于電流的模型，即

(17)

為便于分析，將轉子方程中參數作量綱一化處理，即

式中：kP為比例控制系數；kD為微分控制系數；ωn為轉子的固有頻率；t為時間。

學術界認為，無論是在理念上倡導人類命運共同體意識，還是在實踐上構建人類命運共同體，并不意味著其已成為當代世界的事實判斷[47]，還要準確認識其面臨的諸多困境。

2.4 兩組咳嗽緩解及消失時間比較 治療后，B組的咳嗽緩解時間與咳嗽消失時間均短于A組，差異均有統計學意義(P<0.05)。見表3。

中糧寧夏年產2萬t葡萄酒及配套種植基地項目區生活用水為從事葡萄酒生產101名工作人員生活用水。考慮到企業生產規模現階段無增加的計劃，因此不考慮項目區人口增加。

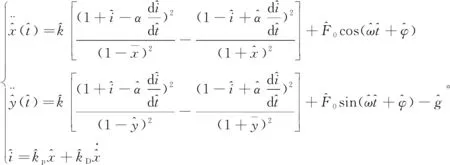
(18)

磁懸浮軸承參數見表1，將其量綱一化并代入(18)式，可得磁懸浮軸承的非線性動力學方程。

表1 磁懸浮軸承參數

2 數值計算結果與分析

(18)式是二階非線性微分方程組，利用Runge-Kutta法可以計算得到轉子的位移響應。利用MATLAB軟件分析渦流參數對轉子的主共振與諧振響應的影響。

當前跨境電商企業最希望招聘的是跨境電商專業對口的人才，但是由于目前鮮有院校專門開設該專業，因此，企業選擇畢業生最多的專業主要是國際貿易74%，電子商務61%，和商務英語45%。

2.1 渦流效應對轉子主共振響應的影響

不同偏心力下，轉子在共振頻率附近的最大振幅隨渦流因子變化曲線如圖3所示。由圖可知，轉子的最大振幅隨偏心力的增大而增大；在同一偏心力下，渦流因子越大，轉子的最大振幅越大。

由上海市高等學校圖書情報工作委員會、上海市圖書館學會、中國索引學會共同主辦，上海師范大學圖書館、湖北三新文化傳媒有限公司三新研究院、江蘇中楊數據科技有限公司共同承辦的2018“圖書館學術論壇”，今天在上海師范大學順利召開。在此，我謹代表上海市高校圖工委和相關主辦、承辦單位，對各位領導、專家學者及與會代表的到來表示熱烈的歡迎！

圖2 不同模型下的頻響曲線

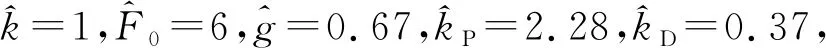
隨著我國的企業的發展和創新，企業的治理結構也在緊隨市場形勢進行優化，從當前公司治理結構來透視企業財務管理目標。暴露出企業很多發展問題，因此在新形勢企業在做好創新和改革的同時，也要積極強化自身內部的人才儲備。選擇專業素質高、文化素質強、領導能力高的人員擔任公司的管理層，不僅可以為企業的發展注入新鮮血液，同時最大限度地提升企業的人才競爭力。對其企業治理結構的升級和財務管理目標的實現都具有重要意義。

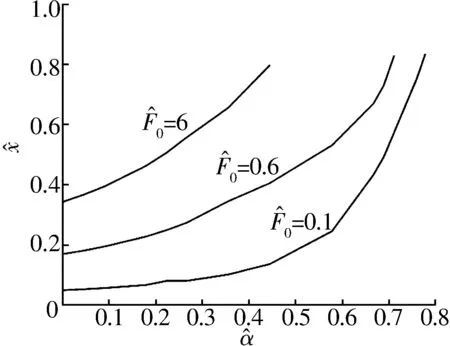
圖3 不同偏心力下轉子振幅隨渦流因子的變化曲線

綜上可知，渦流效應會增強磁懸浮軸承中電磁力的非線性，一方面會使電磁力的“軟彈簧”效應更加嚴重，使主共振的“左偏”現象更突出，甚至出現“跳躍”現象；另一方面，渦流效應會使轉子在主共振點處的振幅進一步增大，該現象在較大偏心力下更加明顯。

2.2 渦流效應對轉子超諧振和次諧振響應的影響

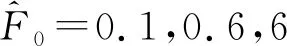
3.4.2 直流電源自身具有完善的蓄電池管理功能，可對蓄電池進行充放電管理，能有效延長蓄電池使用壽命，減少站點蓄電池投資和維護費用。

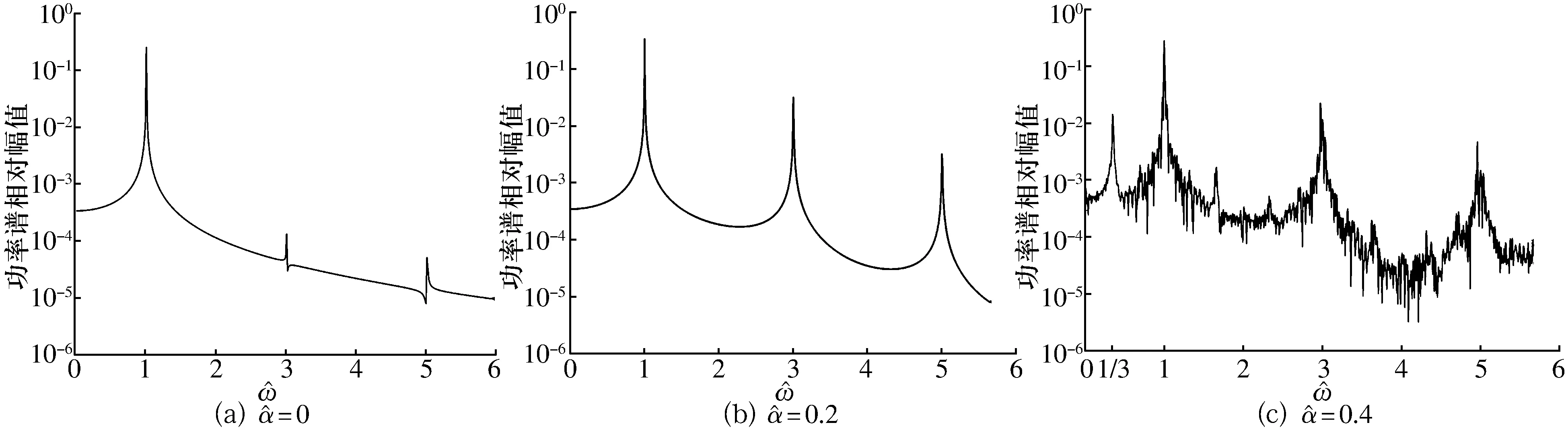
圖不同渦流因子下轉子位移功率譜

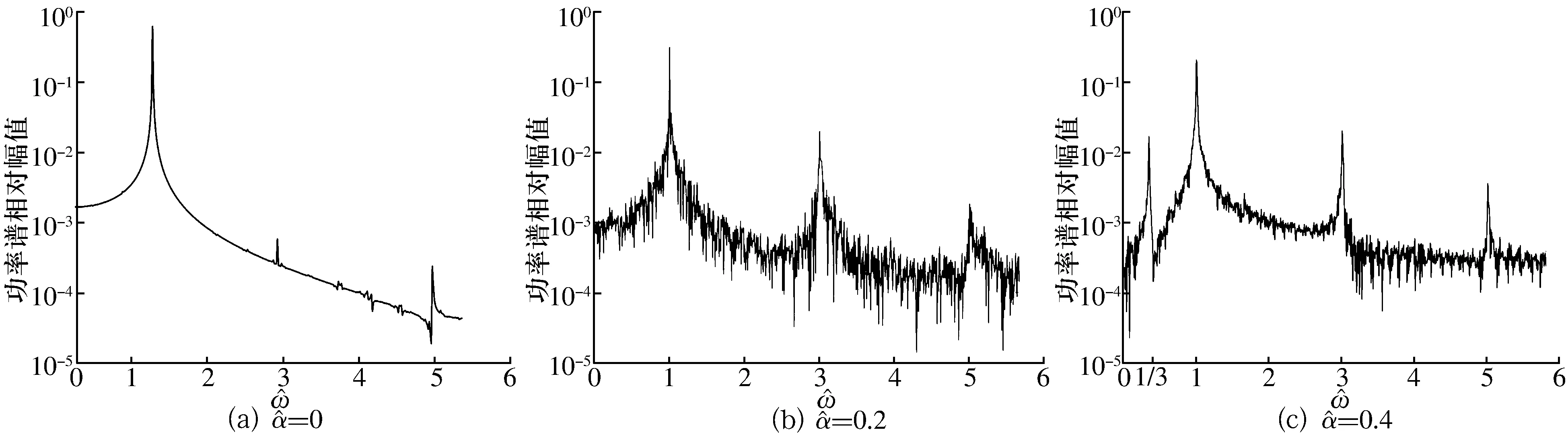
圖不同渦流因子下轉子位移功率譜

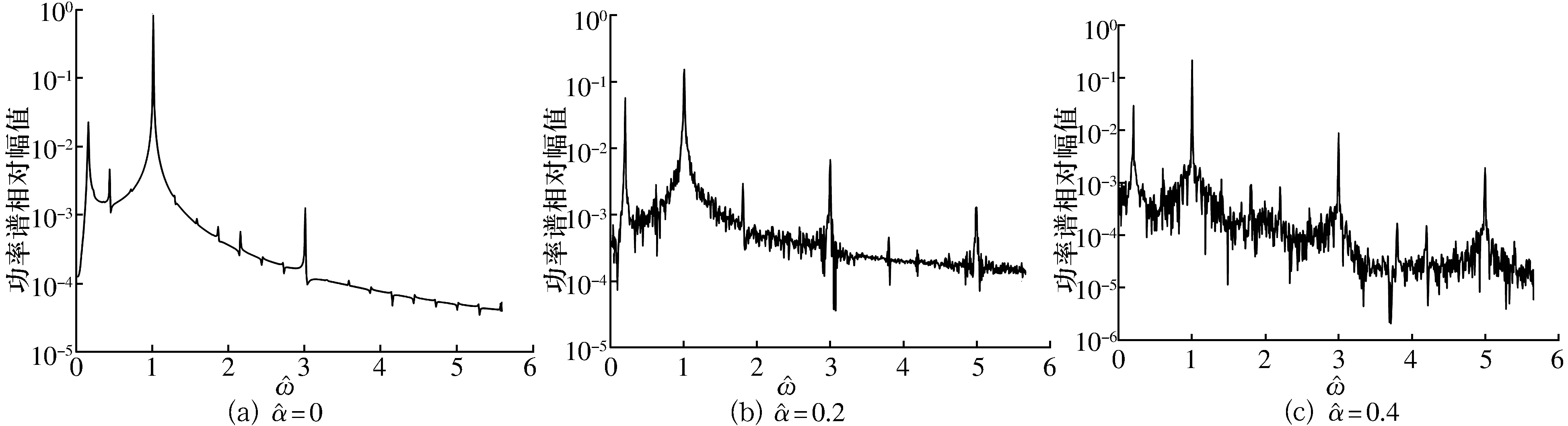
圖不同渦流因子下轉子位移功率譜

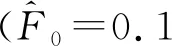
汪安南：在2013年年初召開的全國水利廳局長會議和水利規劃計劃工作視頻會議上，陳雷部長深刻剖析和闡釋了水利工作面臨的新形勢、新機遇和新要求，對做好新形勢下水利規劃計劃工作指明了方向。規劃計劃司切實貫徹落實中央要求和部黨組決策部署，重點開展了以下工作：

3 試驗結果對比

由于渦流效應的結果表現為系統動力學方程中增加的電流微分項，因此，若已知電流微分項對轉子運動的影響，就可得到渦流效應對轉子運動的影響。關于磁懸浮軸承中電流增加微分項后對轉子運動的影響，文獻[15]進行了試驗，結果如圖7所示。由圖7a可知，存在渦流非線性的情況下，磁懸浮軸承的轉子頻響曲線出現了跳躍現象，試驗結果與理論分析結果(圖2b)相似；由圖7b可知，轉子振動位移的頻譜同樣出現了多種倍頻成分，與理論分析結果也相似。

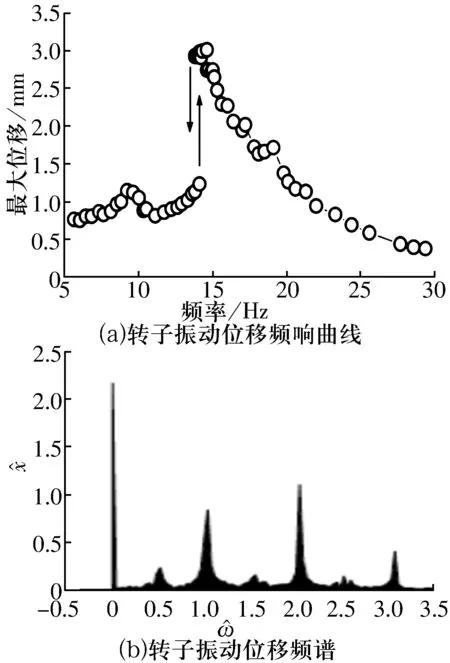
圖7 試驗結果

由此可知：由渦流效應產生的電流微分項對系統運動產生了明顯影響，該微分項使頻響曲線出現了跳躍現象，也使轉子位移頻譜里出現了多種倍頻成分。

4 結論

考慮渦流效應對電磁力的影響，建立了電磁力的時域模型，利用Runge-Kutta法計算了磁懸浮轉子振幅，得到以下結論：

1)渦流效應會引起磁懸浮軸承中電磁力的變化，使得電磁力模型中包含了關于電流的微分項，從而進一步加強了電磁力的非線性。

2)渦流效應會引起轉子的頻響曲線主共振區的變化，使得共振點左移，頻響曲線左偏甚至出現“跳躍”現象，還會增大轉子在共振區的振幅。

3)渦流效應會對轉子的超諧波和次諧波響應產生影響。渦流效應使轉子振幅頻譜中的頻率成分增加，除了主共振以外，還會產生超諧波與次諧波頻率成分，并且增大諧振頻率的響應幅值。