高溫基線密封編織彈簧管的建模與仿真

巴全坤 王維民 姜 鑫 張登鵬

（高端機械裝備健康監控與自愈化北京市重點實驗室，北京化工大學，北京 100029）

0 引言

高超聲速飛行器是指飛行速度超過5 倍聲速的飛機、導彈、炮彈之類的有翼或無翼飛行器，具有突防成功率高的特點，有著巨大的軍事價值和潛在的經濟價值［1］。高超聲速飛行器飛行速度高，由于激波壓縮和粘性摩擦作用，壁面周圍空氣溫度會急劇上升，一旦高溫氣流通過密封部位流入飛行器內部，就會對飛行器內部的不耐溫結構造成破壞，因此必須進行有效的熱防護［2-3］。目前在高超聲速飛行器的活動控制面板處使用的熱防護多為高溫基線密封，該技術在國外已經比較成熟，但我國仍然處于研究階段，高溫熱密封仍然是制約高超聲速飛行器發展的關鍵技術［4］，研究高溫基線密封對我國航空航天業的發展具有重要的意義。

美國NASA 曾在20世紀開展了許多高溫密封的研究，包括NASA-JSC（X-38 項目）、NASA-ARC（熱防護分支）、NASC-KSC（軌道飛行器試驗）、波音密封部門（X-38 項目）和Hi-Temp（密封和熱防護制造）［5］。高溫基線密封主要運用在高聲速飛行器的發動機、起落架、艙門、舵、襟翼等處［6-7］。結構分為三層，外層為Nextel 纖維編織的兩層護套，中間層為Inconel-750 高溫合金編織的彈簧管，內層填充Saffil氧化鋁纖維［8］。其中編織彈簧管為主要的彈性元件，其結構類似于紡織學上的緯編織物，通過平行的Inconel-750 高溫合金絲編織成環形的立體幾何結構。高溫基線密封安裝在活動部位，需要有良好的彈性來保持與密封縫隙兩側的壁面接觸，編織彈簧管作為主要提供回彈性的裝置起著至關重要的作用。

本文主要針對高溫基線密封的主動預緊力裝置編織彈簧管進行仿真分析，研究編織結構與參數對編織彈簧管性能的影響。

1 基線密封設計要求

密封件必須能夠在980～1 204 ℃的高溫氧化環境中使用，盡量減小熱氣流泄露到溫度敏感部位［9］。密封件一般在壓縮狀態下安裝，保證與活動面板兩側緊密貼合，在密封間隙改變時，密封件要有足夠的回彈性來補償間隙變化，但回彈力過大時容易損壞控制面板上的隔熱層，加快結構破壞，同時也會導致控制面板活動所需的驅動力大大增加，因此回彈力要適中。根據密封設計要求（表1）［10］，編織彈簧管需要滿足在各溫度環境下壓縮時的應力盡量小，以避免結構破壞；回彈力盡量大，但不超過最大0.88 N/mm；使用壽命要超過最大使用周期。

表1 密封設計要求Tab.1 Seal design requirements

2 編織彈簧管幾何建模

2.1 幾何結構

編織彈簧管為圓柱形空間立體幾何，為了對編織幾何的參數進行度量，將圓柱形的編織彈簧管展開成平面幾何進行研究。參考紡織學中的緯編織物結構，采用Pierce線圈模型來模擬編織彈簧管中心線的形狀。如圖1所示，Pierce 線圈模型分為針編弧、圈柱、沉降弧［11］。

圖1 Pierce線圈模型Fig.1 Pierce coil model

Pierce 線圈模型是一種比較理想化的假設，其中包括以下幾點［12-13］：

（1）用直線段來模擬圈柱，用圓弧來模擬針編弧和沉降弧；

（2）每個線圈單元為左右對稱，且針編弧與沉降弧的半徑相等，弧長相等；

（3）線圈各處的截面為圓形，且直徑相等。

2.2 結構參數

Pierce 線圈模型由圓形截面和中心線確定，中心線為分段連續光滑曲線，圖2為中心線的1/4模型。

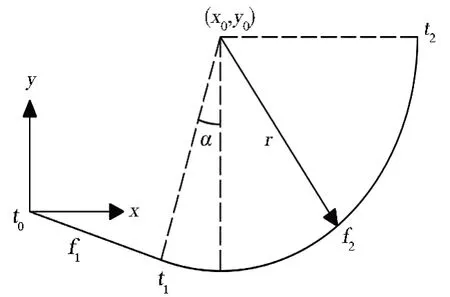
圖2 四分之一中心線模型Fig.2 Quarter centerline model

圖2中的曲線采用規律曲線根據方程創建，規定t為自變量，取值范圍為0～1。該曲線函數分為圈柱中心線函數f1(t)和針編弧中心線函數f2(t)。 圈柱中心線f1(t)的方程：

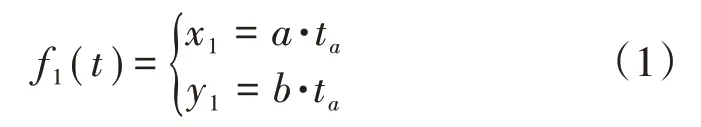
針編弧中心線f2(t)的方程：

式中：

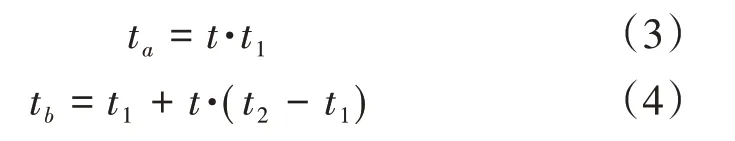
將圖2中的1/4 曲線進行對稱與陣列，得到圖3所示的編織彈簧管中心線的平面展開圖。

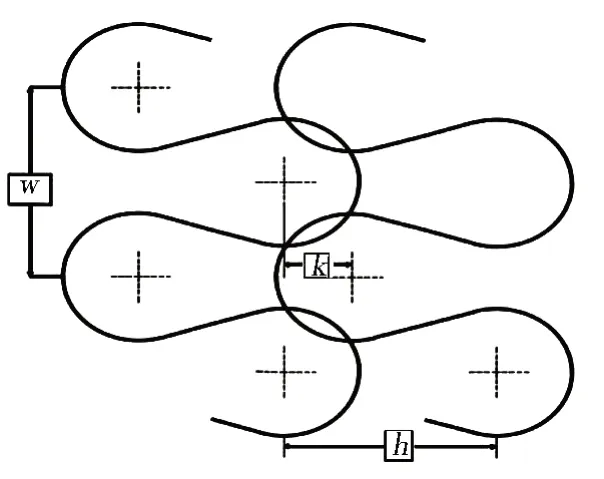
圖3 中心線的平面展開圖Fig.3 Plane plan of centerline

w為兩個沉降弧圓心之間的距離：

D為編織彈簧管的直徑；n為一周Pierce 線圈的數量。

圓心坐標(x0，y0)由以下表達式計算：

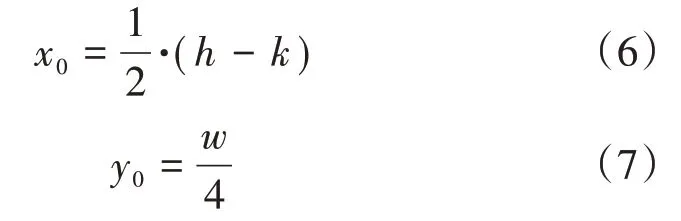
參數t2為最終變量，當t在0～1 上變化時，函數f1(t)和f2(t)正好組成完整的1/4 模型。t2有如下關系式：

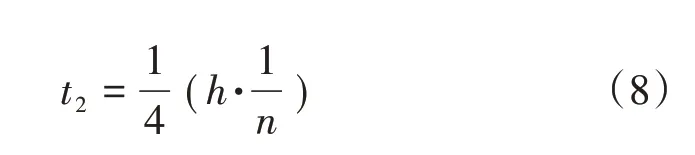
方程（9）、（10）滿足連續性條件：

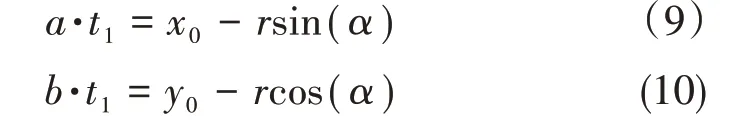
方程（11）、（12）滿足光滑性條件：

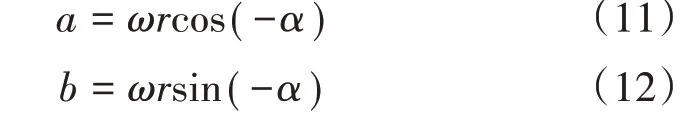
tb=t2時，x′2= 0，得到如下表達式：

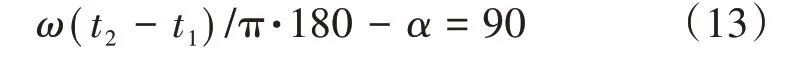
此時有5 個約束方程（9）～（13）和5 個未知數t1、w、α、a、b，故方程有唯一確定的解。

彈簧的剛度還與編織結構有關，編織結構可用環密度LD來度量，其定義公式如下：

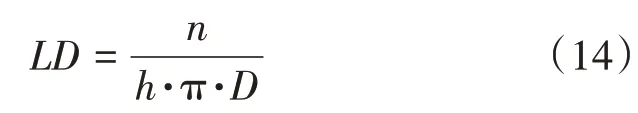
對于編織彈簧管的剩余參數在設計時指定，具體參數如表2所示。將中心線平面曲線纏繞到圓柱面上，得到針編弧與沉降弧的交點，將交點沿著圓柱的半徑方向偏移一個線徑d，構造型值點，通過型值點創建空間非均勻有理B 樣條曲線（NURBS），然后采用光順曲線串方法讓針編弧與圈柱光滑相接。最終得到編織彈簧管的三維模型。

計算時忽略兩端的邊界效應。根據基線密封安裝環境，在彈簧管的上下端各添加一個平板，通過平板的移動來模擬編織彈簧管的壓縮，如圖4所示。

表2 編織彈簧管參數Tab.2 Parameters of braided spring tube

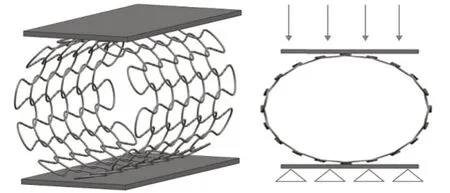
圖4 計算模型Fig.4 Computational model

3 材料特性、網格和邊界條條件

3.1 材料特性

Inconel X-750為鎳基高溫合金，在800 ℃以下具有較高的強度。假設材料為線彈性的，其材料參數如表3所示。

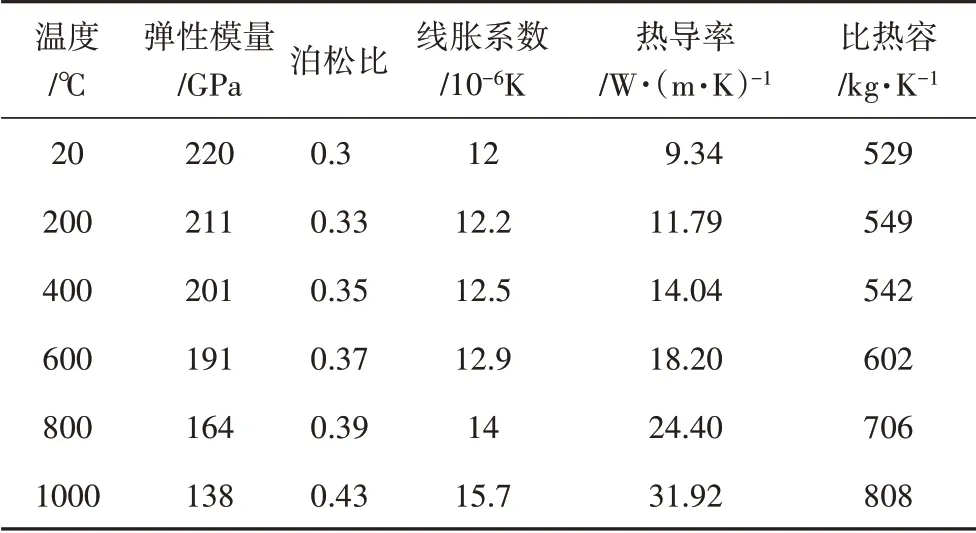
表3 Inconel X-750材料參數［14］Tab.3 Material parameters of Inconel X-750

3.2 網格和邊界條件

模型網格均采用掃掠網格畫法，網格均為高精度的六面體網格，單元采用高階三維20 節點的solid186單元，單元保留中間節點。

編織彈簧安裝在兩平板之間，一個固定，另一個給定位移，用來模擬彈簧管的壓縮過程，該過程分為多個子步施加。接觸約束采用自動識別，自動檢測公差值為0.01 mm，接觸檢測類型為面與面接觸檢測。綁定接觸的接觸算法采用純罰函數算法。摩擦接觸和無摩擦接觸為非線性接觸，收斂困難，均采用增廣拉格朗日算法。

4 結果分析

通過提取上蓋板隨位移變化的回彈力來繪制編織彈簧的位移-載荷曲線，進而對彈簧的剛度進行評估。

4.1 不同接觸類型的影響

針對環密度LD=0.05 和LD=0.10 模型，分別計算了無摩擦、摩擦因數為0.1和綁定等不同接觸狀態對彈簧剛度的影響，計算結果如圖5～圖6所示。

圖5 LD=0.05時不同接觸類型的影響Fig.5 Effects of LD=0.05 different contact

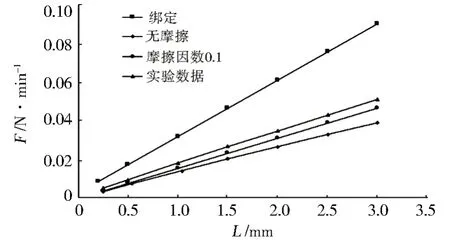
圖6 LD=0.10時不同接觸類型的影響Fig.6 Effects of LD=0.10 different contact

由計算結果可以看出，不管在何種接觸狀態下，編織彈簧的回彈力與壓縮量都呈現出線性關系。選擇接觸摩擦因數為0.1的結果與實驗結果吻合較好。在壓縮量低于1 mm 時，無摩擦接觸和摩擦接觸的結果相差很小，接觸之間的摩擦力對彈簧剛度的影響很小。綁定接觸使編織彈簧的剛度大大增加，其計算結果與實驗結果相差甚遠。

4.2 不同環密度的影響

由環密度LD的定義公式可以看出，環密度越大，編織越密集，計算了LD=0.05 和LD=0.10 模型。在接觸同為摩擦因數為0.1的結果如圖7所示。

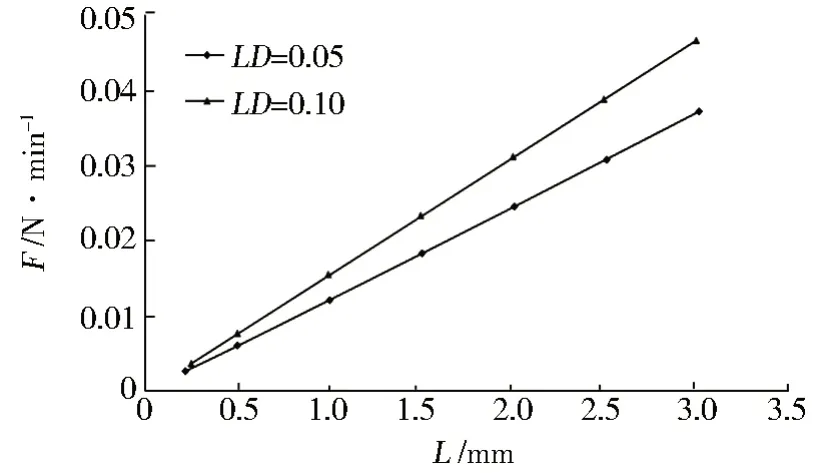
圖7 環密度的影響Fig.7 Influence of ring density

從計算結果可看出，通過增加環密度對彈簧剛度的影響較小，在3 mm的壓縮量下，環密度LD=0.10模型比環密度LD=0.05模型的回彈力高約20%。

4.3 不同線徑的影響

針對環密度LD=0.05 的模型，分別對線徑為0.23、0.32、0.40 mm的模型進行計算，得到的結果如圖8～9所示。

圖8 線徑對剛度的影響Fig.8 Effect of wire diameter on stiffness

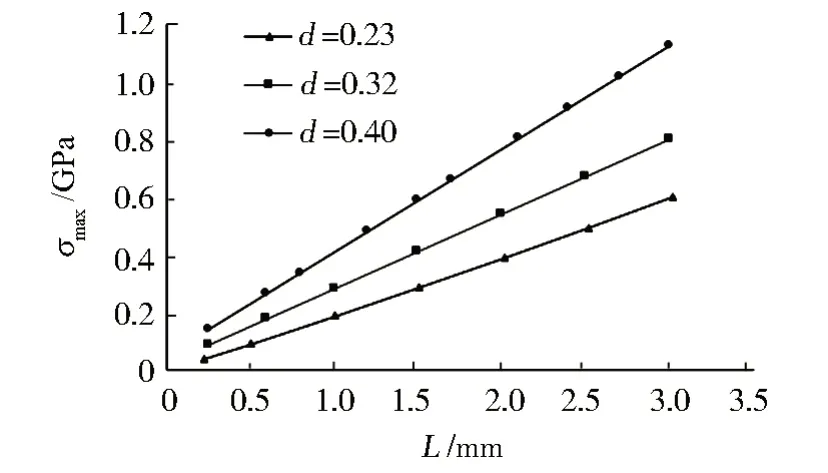
圖9 線徑對應力的影響Fig.9 Effect of wire diameter on stress

某一線徑下編織彈簧回彈力與壓縮量仍然呈線性關系，但不同線徑下彈簧的回彈力與線徑表現為非線性高次關系，回彈力隨著線徑的增加急劇地增加。線徑從0.23 變到0.32 mm，回彈力增加了約6倍；線徑從0.23 變到0.40 mm，回彈力增加了約11倍。但隨著線徑的增加，在同樣壓縮量下的最大應力也急劇增加，應力過大會造成結構破壞，故線徑的選擇也不宜過大，推薦使用0.32mm的線徑。

4.4 不同編織股數的影響

本次計算模型均為單股編織，故需要將多股編織簡化成單股編織。通過等效面積法來確定單股編織的直徑，等效公式如下：

式中，d為單股線徑，N為多股編織時的股數，d′為多股編織時等效成單股編織的直徑。

等效面積下單線模型與多股編織模型相比，其結構是連續的，受力均勻，故其剛度要比多股編織模型高，因此必須對單股模型的剛度進行修正。假設多股編織的彈簧線之間的影響可以忽略不計，在受力彎曲時，彈簧線截面上的剪力對彎曲變形的影響可以忽略，故對單股模型進行修正時將其簡化成純彎曲結構。純彎曲靜力平衡公式：

根據等效原則，多股編織模型和單股模型在相同壓縮量下，其變形后的曲率1/ρ、所承受的彎矩M、抗彎剛度EI均應相等。假設EI為多股編織模型中每股的抗彎剛度，則多股編織的抗彎剛度E1I1=NEI，即I1=NI。圓形截面的截面慣性矩公式如下：

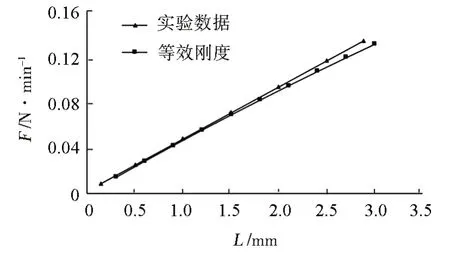
圖10 剛度修正Fig.10 Influence of wire number

不同編織股數采用等效面積與等效剛度后的計算結果如圖11所示。

圖11 不同編織股數的影響Fig.11 Effect of the number of braided strands

從計算結果可以看出，增加編織股數，單位長度回彈力明顯增加，從單線變雙線，回彈力增加2.13倍，從單線變三線，回彈力增加3.54倍。但是隨著編織股數的增加，應力也快速增大，因此編織股數也不宜過多，推薦使用雙線編織。

4.5 不同溫度的影響

為了研究溫度對彈簧剛度的影響，對環密度LD=0.05 的編織彈簧管計算其在常溫、200、400、600、700、800、900、1 000℃下壓縮3 mm 時的回彈力，得到如圖12的計算結果。

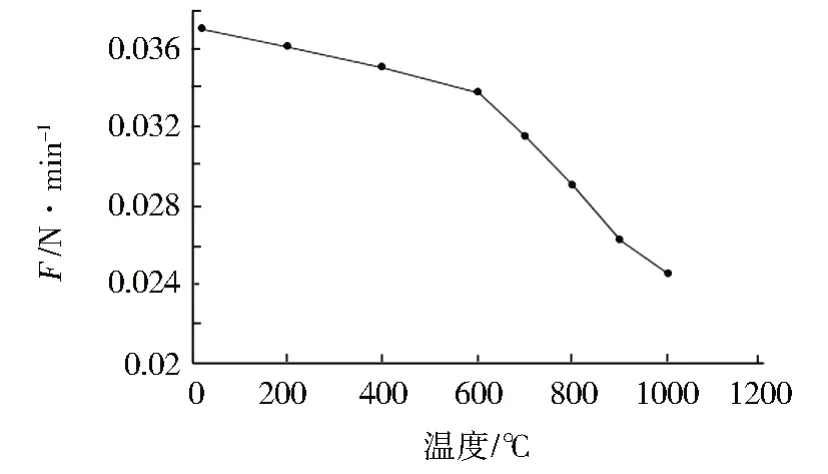
圖12 溫度的影響Fig.12 Influence of temperature

由計算結果可以看出，隨著溫度的升高，編織彈簧管的回彈力逐漸下降，其在600 ℃以下時，回彈力下降的速度相對較小，在600～900 ℃時，下降速度明顯增加，在高于900 ℃后，回彈力的下降速度有所減小，但仍然比溫度在600 ℃以下時的下降速度快。

4.6 疲勞壽命

環密度LD=0.05 的編織彈簧管在650 ℃下的靜力分析結果如圖13～14所示。

圖13 應變云圖Fig.13 Strain nephogram

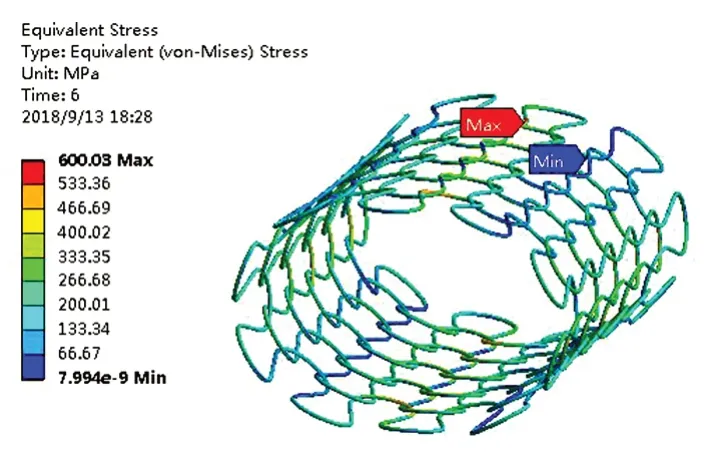
圖14 應力云圖Fig.14 Stress nephogram

由圖可知，最大應變為0.3%（較小），最大應力為600 MPa（較大），因此疲勞計算時采用應力-壽命曲線（S-N曲線）來表示應力與失效循環的關系。采用國產GH4169高溫鎳基合金在總應變范圍為1%時的S-N曲線來代替計算，S-N曲線如圖15所示［15］。

圖15 S-N曲線Fig.15 S-N curve

疲勞載荷類型選用脈動循環定義，設計壽命為106。計算得到的疲勞壽命云圖如圖16所示。

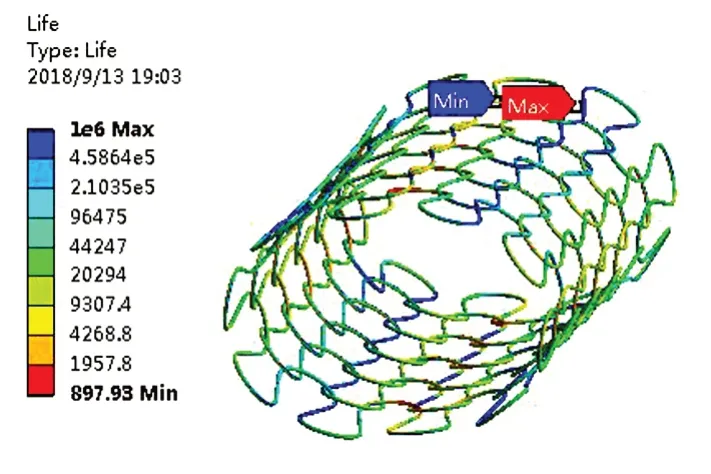
圖16 壽命云圖Fig.16 Life nephogram

由圖可以看出，編織彈簧管的最小壽命發生在編織彈簧最高與最低的針編弧上，最小壽命為898次循環，滿足密封設計要求。

5 結論

參照Pierce 線圈模型對編織彈簧管進行參數化建模，對比有限元計算結果與實驗數據，該模型可有效地對彈簧剛度進行預測。接觸面摩擦因數為0.1時能較好吻合實驗結果。

（1）彈簧剛度對線徑十分敏感，回彈力與線徑表現為非線性高次關系，增大線徑能獲得很大的剛度增強。如果設計的彈簧管回彈力不夠，通過增加線徑能得到很好的效果。

（2）對多股編織模型可通過等效面積與等效剛度轉化成單股編織模型，能使建模與計算大大簡化。從單線變成多線編織，回彈力成倍增加。

（3）溫度低于600 ℃時彈簧的剛度變化很小，高于600 ℃后，彈簧剛度隨著溫度升高快速下降，這與材料的高溫特性有關，可以通過選用更耐溫的材料來進行改善。

（4）通過S-N曲線計算的最低疲勞壽命高于密封設計要求，該計算可為編織彈簧管的合理使用提供有利參考。

（5）為滿足編織彈簧管在各溫度下壓縮時的應力盡量小、回彈力盡量大、但不超過最大0.88 N/mm的設計要求，推薦使用環密度LD=0.05、線徑為0.32 mm、雙線編織的參數來制作編織彈簧管。