(0.5-100)mm量塊中心長度測量結果的擴展不確定度評定
齊皇仲 陸韜
浙江省方正校準有限公司 浙江杭州 310013
量塊作為一種實物量具,能夠提供一個非常穩定的端度類測量標準,我們制造類企業在實際生產中經常需要用到量塊或者用于比對測量產品,或者用于校對量具,應用可謂廣泛。因此對量塊的校準就有廣泛的需求,而校準量塊就必須評定其測量不確定度[1]。
1 概述
測量依據:JJG146-2011《量塊檢定規程》。
測量條件:溫度(20±0.6),相對濕度≤65%。
計量標準:(0.5-100)mm3等量塊。
被測對象:(0.5-100)mm4等量塊。
測量方法:為使標準量塊和被測量塊的溫度達到近似相等,測量前兩量塊需同時放置在工作臺上等溫。測量時,先將標準量塊放入量塊比較儀下,比較儀置零,再移至被測量塊,得到與標準量塊中心長度差值δ。δ與標準量塊中心長度的實際值Ls之和即為被測量塊中心長度的實測結果L。
2 測量模型
L=δ+Ls
式中:L-被測量塊中心長度,單位:mm;
δ-被測量塊與標準量塊中心長度差值,單位:mm;
Ls-標準量塊中心長度,單位:mm。
3 不確定度傳播率

式中δ的靈敏系數c1=?L/?δ=1
Ls的靈敏系數c2=?L/?Ls=1
4 輸入量的標準不確定度評定
4.1 輸入量δ標準不確定度u(δ)的評定
輸入量δ的標準不確定度來源由3個不確定度分量構成;
a測量重復性引起的標準不確定度u(δ1);
b標準和被測量塊的線膨脹系數之差Δα引起的標準不確定度u(δ2);
c標準量塊與被測量塊溫度差Δt引起的標準不確定度u(δ3);
(1)u(δ1)的評定。測量重復性引入的標準不確定度采用A類方法評定,選取100mm量塊1塊,用量塊比較儀在重復性條件下連續比較測量10次,得到測量列0.62,0.69,0.73,0.58,0.55,0.64,0.59,0.62,0.65,0.63,單位:μm。按貝塞爾公式計算,得到單次實驗標準差S=u(δ1):

同理可得10mm量塊的測量重復性引入的標準不確定度26nm、50mm量塊的測量重復性引入的標準不確定度33nm。
自由度均為:
ν(δ1)=10-1=9
(2)u(δ2)的評定。從規程得知,量塊所用鋼材料的線膨脹系數應為(11.5±1)×10-6℃-1,被測量塊溫度tx與標準溫度20℃的偏差不超過0.6℃。假定標準和被測量塊的線膨脹系數在(11.5±1)×10-6℃-1范圍內均勻分布,半寬區間α為1×10-6℃-1,標準不確定度u(δ2)為

則對于100mm量塊:

同理可得10mm量塊的u δ2)=4nm、50mm量塊的u(δ2)=18nm。
估計其相對標準不確定度為10%,則自由度為:
ν(δ2)=1/(2×0.12)=50
(3)u(δ3)的評定。原則上要求標準量塊與被測量塊溫度達到等溫后進行測量。但實際測量時,兩量塊通常有一定的溫差Δt,估計溫差在±0.1℃范圍內,且均勻分布,則該分布半寬α為0.1℃,故由Δt引起的標準不確定度u(δ3)為:

對于100mm量塊:
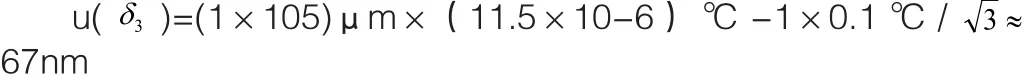
同理可得10mm量塊的u(δ3)=7nm、50mm量塊的u(δ3)=33nm。
估計u(δ3)的相對標準不確定度為10%,則其自由度:
ν(δ3)=1/(2×0.12)=50
(4)合成標準不確定度uc(δ)的計算。對于100mm量塊:

同理可得10mm量塊的uc(δ)=27nm、50mm量塊的uc(δ)=50nm。
合成自由度公式為:
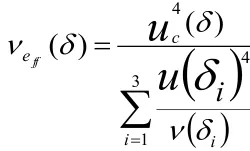
則得 到10mm量塊的νeff(δ)=10、50mm量 塊的νeff(δ)=39、100mm量塊的νeff(δ)=100。
4.2 輸入量Ls標準不確定度u(LS)的評定
標準量塊中心長度Ls的標準不確定度u(Ls)及其自由度取自3等量塊溯源證書中擴展不確定度評定結果[2-3]。結果如下:
10mm量塊的u(LS)=32nm、50mm量塊的u(LS)=49nm、100mm量塊的u(LS)=57nm。
10mm量塊的ν(Ls)=100、50mm量塊的ν(Ls)=100、100mm量塊的ν(Ls)=100。
5 合成標準不確定度uc的評定,見表1
合成標準不確定度公式:

合成自由度公式:


表1 輸入量的標準不確定度匯總一覽表
uc與νeff計算結果如下:
10mm量塊的uc=42nm、50mm量塊的uc=70nm、100mm量塊的uc=104nm。
10mm量塊的νeff=25、50mm量塊的=100、100mm量塊的=100。
6 擴展不確定度Up的計算
Up=kp·uc=tp(νeff)·uc
取置信概率P=0.99,查表可得kp值。

表2 各尺寸Up一覽表
7 校準和測量能力(CMC)
4等量塊校準和測量能力(CMC)為:
(0.5-100)mm:U=0.08μm+1.4×10-6×ln,k=2。(ln為校準點量塊的標稱長度,單位:μm)
8 結語
希望本文能為大家在評定量塊中心長度測量結果的擴展不確定度的工作中提供一些參考。

