基于鄧肯-張模型的飽和土統計損傷模擬方法研究
黃安邦,魏良帥,賈 逸,和 銘,王家柱,黃海峰
(1.中國地質科學院探礦工藝研究所,四川成都611734;2.中國地質調查局地質災害防治技術中心,四川成都611734;3.中國地質調查局成都地質調查中心,四川成都610081;4.四川省川北高速公路股份有限公司,四川成都610041)
0 引 言
飽和土的變形過程的模擬辨識一直是土力學研究的難點與熱點之一[1-2]。隨著連續損傷理論的發展,損傷理論逐漸被引入到巖土材料本構模型中。沈珠江等[3]將巖土材料抽象為結構塊體和結構帶2個部分,并認為這2個部分共同承擔巖土體的宏觀應力,其分擔的比例由破損參數決定,進而從微觀視角闡述了巖土材料的變形承載機理;趙錫宏等[4]基于結構性軟土三軸試驗,引入Lemaitre[5]應變等價性假說,獲得彈塑性損傷本構模型;Krajcinovic、唐春安和曹文貴等[6- 8]結合了統計強度理論和連續損傷力學,構建了可反映巖土材料變形破壞全過程的統計損傷本構模型。上述工作使巖土材料損傷本構模型的研究方法在某種程度上實現了從宏觀到細觀的轉變。目前,水電工程、邊坡工程數值計算廣泛使用鄧肯-張模型,可從一定程度上反映土體變形的非線性和彈塑性,模型參數物理意義明確且易通過試驗確定。但是,鄧肯-張模型是建立在增量廣義Hooke定律基礎上的變模量彈性模型,未能考慮土的力學性態的變化。
本文在鄧肯-張雙曲線模型的基礎上,引入統計損傷理論,建立一種新的飽和土統計損傷本構模型,利用該模型模擬飽和土變形全過程,可在一定程度上彌補鄧肯-張模型難以反映土體力學性態變化的不足,以期為飽和土損傷本構模型的構建提供一種新思路。本文模型參數由鄧肯-張模型參數和統計分布參數組成,前者可依據試驗結果確定,后者可通過擬合回歸的方法求取,并根據飽和土的工程特點,探討模型統計分布參數與圍壓的變化關系,以此提出模型的修正方法。
1 常規三軸固結排水試驗
采用長春試驗機研究所研制的CSS-2901TS型土體三軸流變試驗機(見圖1)進行室內固結排水常規三軸壓縮試驗。試驗土樣取自某水電站壩肩傾倒變形邊坡層間破碎帶內,該破碎帶土體為板巖、千枚巖等風化后產物。土樣經過自然風干后碾散,過1 mm 篩,采用擊實法制備重塑土樣。以真空飽水制備土樣,制樣規格為φ40 mm×80 mm。土樣基本物理力學參數:平均濕密度為2.07 g/cm3,干密度為1.58 g/cm3,孔隙比為1.5,壓縮模量為24.157 MPa,粘聚力為0.035 MPa,內摩擦角為20°。

圖1 試驗裝置
根據土樣實際所處應力環境,將圍壓設置為100、200、300 kPa和400 kPa。試驗結果見圖2。從圖2可看出,該飽和土體應力-應變曲線大致呈雙曲線形態,在應力水平較低時,近似表現為線彈性,隨著應力水平的提高,逐漸表現為非線彈性。因此可將損傷理解為土體力學性態的變化和發展,而傳統的鄧肯-張模型利用一種雙曲線函數描述應力-應變關系,其結構簡單、參數較少,但未能反映土體力學性態的變化。統計損傷理論可將其簡化為連續不可逆的損傷過程,以土體力學性態的變化和發展來研究土體變形破壞過程。
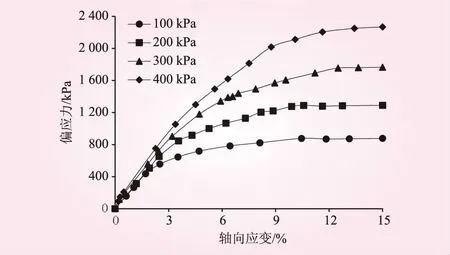
圖2 常規三軸應力-應變關系
2 飽和土統計損傷本構模型
2.1 鄧肯-張模型及損傷變量的定義
Lemaitre[5]等效應變原理的核心假定是宏觀應力σ引起損傷材料上的應變ε和有效應力σ′引起無損材料的應變ε′相等,即
ε=ε′
(1)
考慮土體三向應力狀態,則有
σ′=σ/(1-D)
(2)
式中,D為損傷變量。
假設土體材料由q(q→∞)個微單元組成,微單元僅由p個破壞單元和(q-p)個無損單元組成。假設破壞單元無法承受荷載,無損單元在一定條件下可以轉化為破壞單元,破壞單元和無損單元面積都為S,則損傷變量D可定義為
(3)
式中,0≤p≤q,故D∈[0,1]。
在鄧肯-張模型中,應力-應變關系表示為
(4)
式中,a、b為相關試驗參數。
結合式(2)、(4)可得
(5)
通過式(3)定義土體損傷變量可行性較低,土體破壞單元面積難以精確確定,由此假設土體微元強度的隨機分布變量F=f(σ′)[8-9]服從某種概率密度函數P(F),則其損傷變量D為
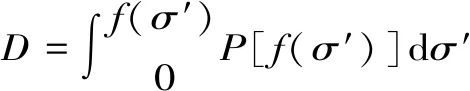
(6)
2.2 本構模型的建立
統計分布主要有Weibull分布、正態分布、冪函數分布、對數正態分布[8-11]等,Weibull分布參數較少,形式簡單,其概率密度函數為
(7)
式中,m、F0為統計分布參數。
將式(7)代入式(6)可得
(8)
參考文獻[8-9],考慮到飽和土的破壞特征以及材料破壞屈服準則的可計算性,選取Mises屈服強度準則將微元強度F表示為
(9)
式中,J2為應力偏量第二不變量,由巖土塑性力學原理[3]可知
(10)
考慮假三軸試驗條件,則有
(11)
綜合式(5)、(8)可得
(12)
式(12)即本文所建立的飽和土統計損傷本構模型。
3 模型參數求解
本文所建模型包含a、b、m和F0等參數。其中,a、b為鄧肯-張模型參數,可通過試驗結果確定;m、F0為統計分布參數。
3.1 a、b的確定
通過式(5)可求得初始切線模量Eu,即
(13)
由于當ε=0時,在試驗的起始點,此時t=0,對應土體的初始無損狀態,所以損傷變量D=0,故式(13)可變形為
(14)
圖2中近似雙曲線的應力-應變曲線的極限偏差應力(σ1-σ3)ult為
(15)
由于實際試驗中不可能使ε無窮大,往往根據15%的應變值來確定土體的強度,此時土體并未完全損傷破壞,實際損傷未達到1,極限偏差應力(σ1-σ3)ult應在一個約束范圍,即
(16)
化簡式(16)為
(17)
考慮到模型參數的可計算性和極限偏差應力的極限特性,將極限偏差應力(σ1-σ3)ult取最大值,即
(18)
由式(14)、(18)可知,a為本試驗中初始切線模量Eu的倒數,b代表雙曲線的漸近線所對應的極限偏差應力(σ1-σ3)ult的倒數。式(14)、(18)即為參數a、b的確定方法。a、b求解過程見圖3(以圍壓400 kPa為例)。a、b求解結果見表1。
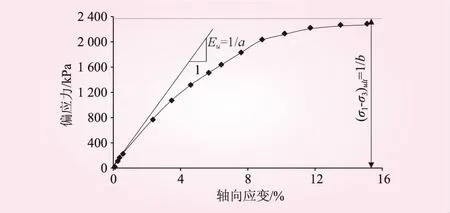
圖3 參數a和b求解
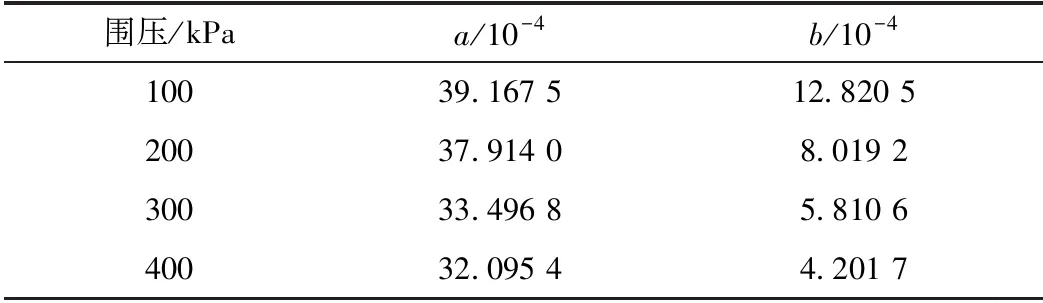
圍壓/kPaa/10-4b/10-410039.167 512.820 520037.914 08.019 230033.496 85.810 640032.095 44.201 7
3.2 m、F0的確定
將式(12)變形為
(19)
對式(19)兩邊同時取對數可得
(20)
繼續對式(20)兩邊同時取對數得
(21)
式(21)可變形為
Y=mX+N
(22)
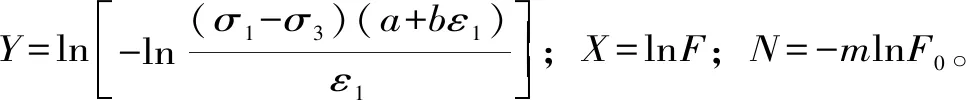
式(19)~(22)即為基于線性方程系數回歸求解的曲線擬合法,可擬合求解參數m、F0。擬合結果見表2。
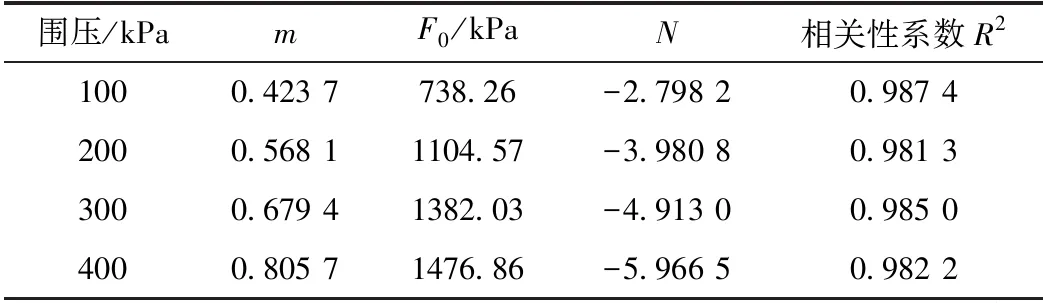
表2 m、F0擬合結果
3.3 模型修正
以表2中的模型參數m、F0作為函數因變量,以圍壓σ3作為函數自變量,分別繪制模型參數m、F0與圍壓σ3的關系曲線,見圖4、5。由圖4、5可知,m與σ3滿足線性關系,其相關性系數R2為0.997 5,F0與σ3滿足二次拋物線曲線關系,其相關性系數R2為0.998 7。將式(23)代入式(12)便可得到修正后的能反映差異性圍壓環境的統計損傷本構模型。通過擬合回歸得到本文統計損傷模型中參數m、F0的修正公式,即
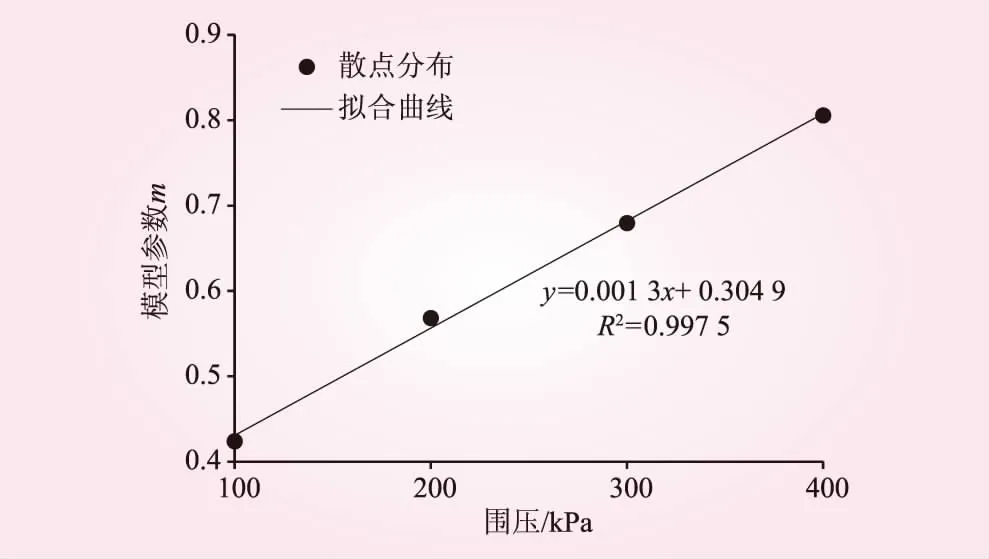
圖4 m與 σ3的關系
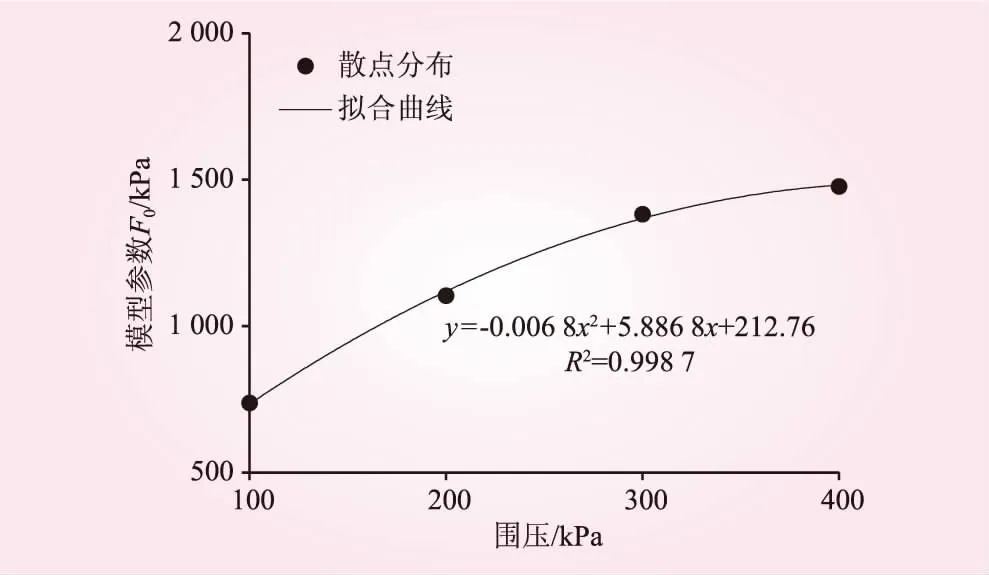
圖5 F0與 σ3的關系
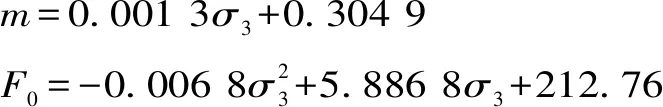
(23)
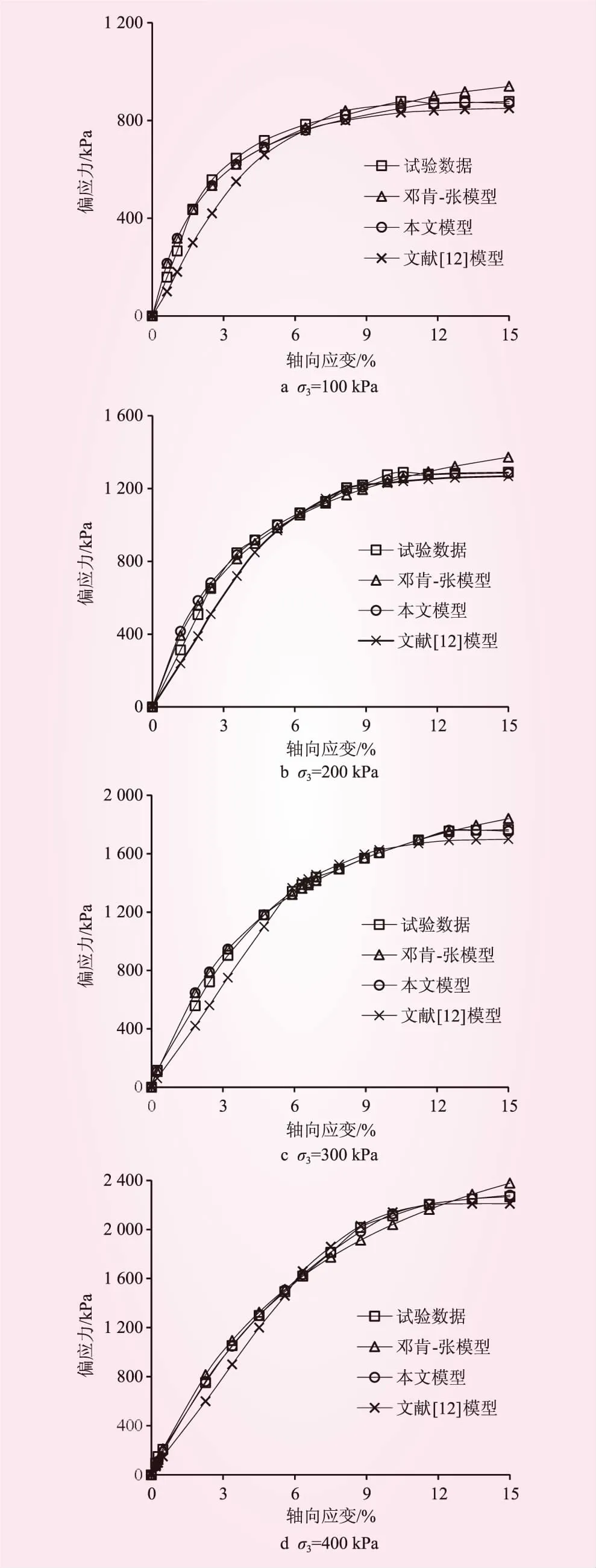
圖6 驗證結果對比
4 模型驗證分析
利用本文所建模型、鄧肯-張模型及文獻[12]中的PZ-Ⅲ彈塑性修正模型,對傾倒變形邊坡層間破碎帶飽和土體的三軸壓縮試驗數據進行驗證,驗證結果見圖6。由圖6可知,文獻[12]中的PZ-Ⅲ彈塑性修正模型擬合精度較低,在軸向應變0.06之前,理論曲線明顯偏離試驗曲線。鄧肯-張模型在軸向應變0.12~0.15之間對試驗數據的辨識能力較差,理論值高于試驗值。相比于PZ-Ⅲ修正模型和鄧肯-張模型,本文所建模型能較好地擬合理論曲線,擬合精度較高。
為了驗證本文模型的適用性,引入文獻[9]中飽和土固結排水三軸壓縮試驗數據,利用本文所建模型對其進行驗證,驗證結果見圖7。從圖7可知,本文模型曲線與試驗數據曲線吻合較好,擬合精度較高。綜合圖6、7,本文所建模型對于飽和土變形過程的模擬辨識具有較強的適用性。
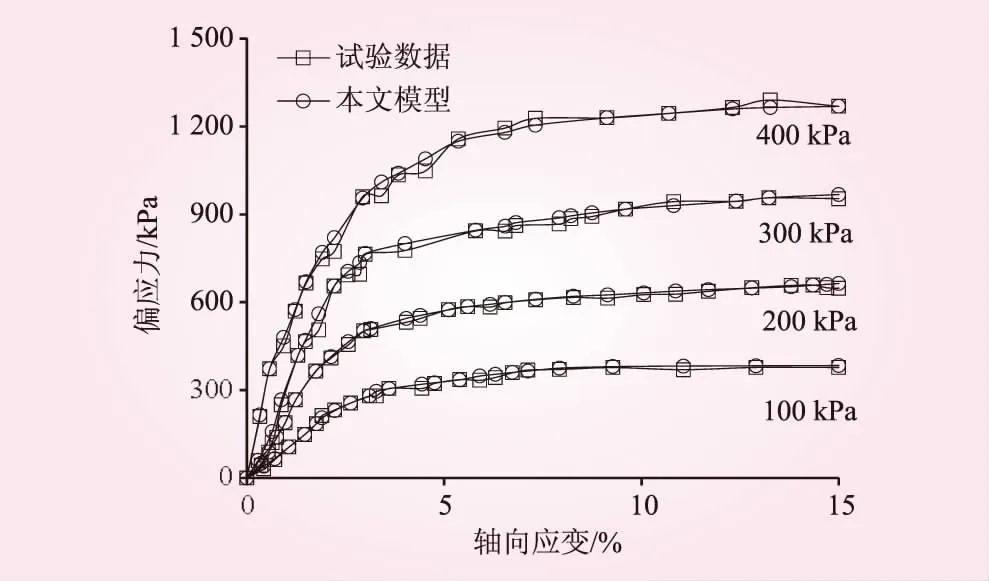
圖7 驗證結果對比
5 結 語
本文基于鄧肯-張模型和統計損傷理論,對飽和土變形模擬進行了研究,得出以下結論:
(1)結合飽和土的工程特點,基于鄧肯-張模型,引入統計損傷理論,彌補了鄧肯-張模型難以反映土體力學性態變化的不足,建立了一種新的飽和土統計損傷本構模型。
(2)依據鄧肯-張模型自身特性和回歸求解的曲線擬合法,確定模型參數,基于參數m、F0與圍壓的關系,對模型進行修正,使其可反映差異性圍壓環境。
(3)所建模型結構簡單,參數較少,便于應用,模型驗證也表明了本文所建模型的合理性和適用性。

