第三代輪轂軸承凸緣端面跳動的測量

陳於學，沙偉，張黎,趙興新, 趙晨昱

(1.華中科技大學 機械學院儀器系，武漢 430074;2.重慶長江軸承股份有限公司，重慶 401336)

輪轂軸承單元是汽車的關鍵零部件，其質量的優(yōu)劣直接影響整車的運行性能。汽車用第三代輪轂軸承單元(以下簡稱輪轂軸承)的主要組成部分有內圈、鋼球、保持架、外凸緣、凸緣、車輪螺栓等。輪轂軸承凸緣通過螺栓與制動盤輪輞連接。凸緣端面的跳動會產生不平衡慣量,使車輪產生離心力，此離心力的方向隨車輪的轉動而變化,對車輛的動、靜態(tài)特性產生嚴重的影響[1-2]。目前，采用檢測人員手動旋轉軸承，通過人眼觀察扭簧表讀數(shù)確定檢測數(shù)值的方法進行端面跳動的測量，這種方法比較繁瑣且人為因素對測量結果的影響比較大[3]。同時，不同型號輪轂軸承凸緣端面具有不同數(shù)量的缺口，這些缺口的存在大大增加了人工測量的難度。

綜上，提出一種新型的以LabVIEW為平臺的輪轂軸承凸緣端面跳動測量方法，可以有效消除由于安裝和裝置本身端面傾斜導致的系統(tǒng)誤差，從而得到準確的端面跳動測量結果[4]。

1 測量原理

如圖1所示，不同型號輪轂軸承的凸緣端面可以分為連續(xù)端面和離散端面2大類，或者無缺口型、單缺口型、四缺口型3小種。

圖1 不同端面的輪轂軸承凸緣

1.1 測量方法

根據(jù)輪轂軸承凸緣端面上的螺栓實際安裝情況，并結合大量的試驗，采用如圖2所示的測量原理。利用一面兩孔定位原理定位被測物，將被測軸承置于放置平臺，然后將被測軸承上的車輪螺栓插入放置平臺的孔中，再利用鎖緊螺母將被測軸承鎖緊。傳感器垂直接觸輪轂軸承凸緣端面，通過靜壓主軸帶動被測軸承一起勻速旋轉，測量輪轂軸承凸緣端面上的整個圓周。3種不同形狀端面的測量結果如圖3所示。

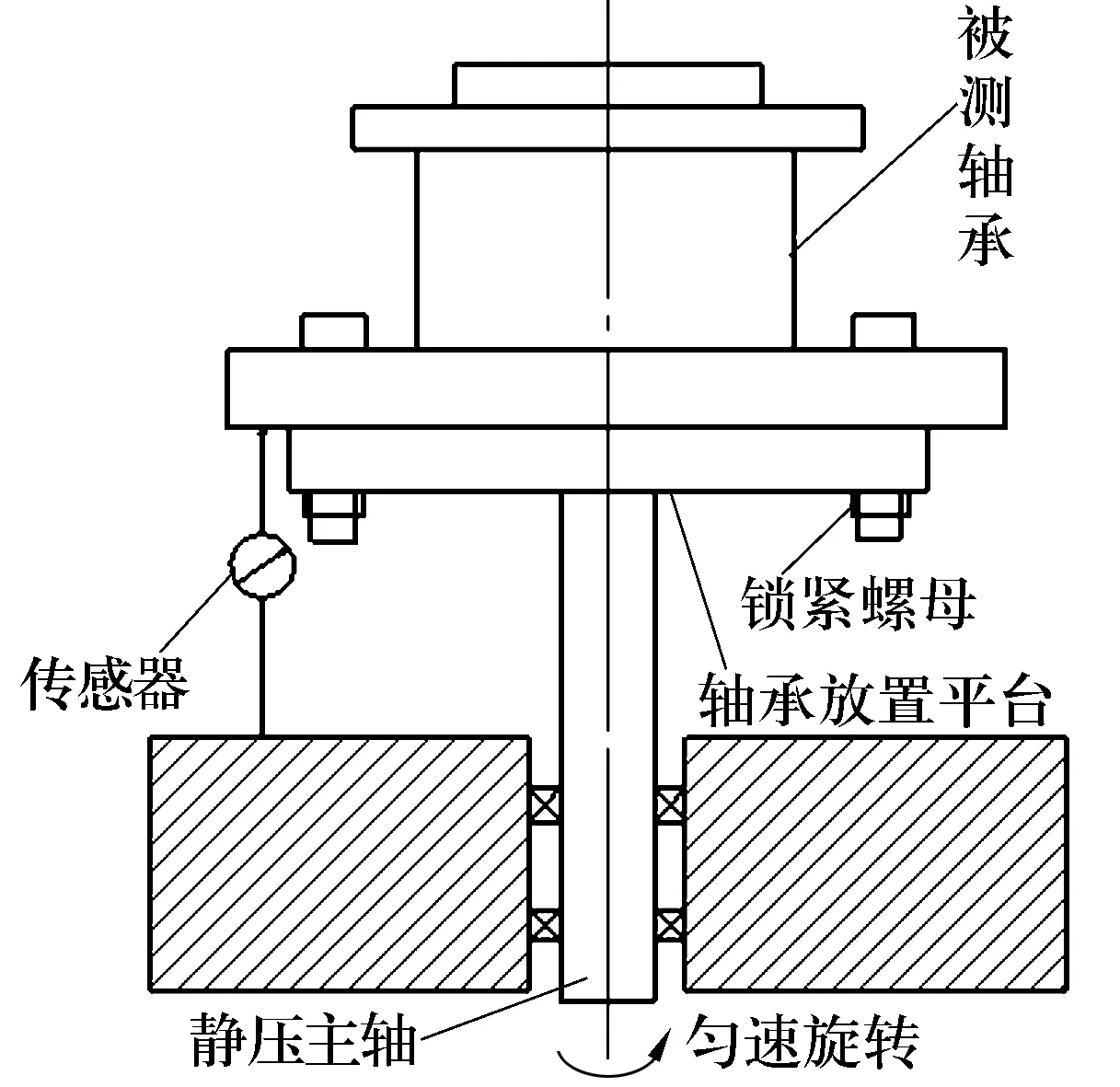
圖2 輪轂軸承凸緣端面跳動測量原理示意圖

實際測量得到的3種波形呈現(xiàn)正弦波形趨勢，如果采集更多圈數(shù)，正弦波形就會周期性的波動下去，符合旋轉零件的測量情況[5]。但是，這種宏觀上的正弦變化并不是輪轂軸承凸緣端面跳動量的實際情況，這是由于輪轂軸承安裝平臺的傾斜或者安裝軸承時軸承軸線傾斜所導致的結果。

圖3 輪轂軸承凸緣端面跳動采集數(shù)據(jù)

1.2 誤差消除和凸緣端面跳動獲取

1.2.1 端面測量中的誤差分析

如圖4所示，測量中端面保持理想水平，直接測量得到的就是實際的端面跳動量S。理想情況下得到的測量數(shù)據(jù)應當是一條直線，位移傳感器的示值始終為初始值P0，如圖5所示。但在實際測量過程中，被測軸承的凸緣端面可能是傾斜的，導致位移傳感器觸頭與被測軸承凸緣端面接觸點的空間運動軌跡是一個橢圓,這種情況下的測量數(shù)據(jù)不是端面的真實跳動量。

圖4 被測軸承測量示意圖

圖5 理想水平測量數(shù)據(jù)

測量過程簡化的模型如圖6所示，此運動軌跡可以看作由一個圓柱和一個空間平面斜相交所導致。設圓柱和空間平面的方程分別為

x2+y2=R2，

(1)

Ax+By+Cz=D，

(2)

式中：R為位移傳感器觸頭到軸線的垂直距離；A,B,C,D為常數(shù)且不等于0。

圖6 輪轂軸承凸緣端面被測點在空間的運動軌跡

再令x=Rcost,y=Rsint,t∈(0,2π)，代入(2)式化簡可得

z=P0-δsin(t+θ)，

(3)

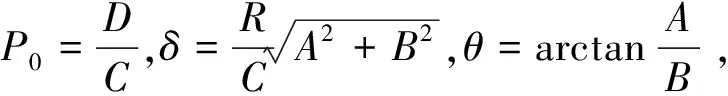
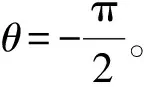
由于位移傳感器的示值只與z軸方向變化有關，(3)式中z的變化就是位移傳感器示值的變化，其表達式也證明了如果軸承凸緣端面出現(xiàn)圖4中的傾斜，測量得到的數(shù)據(jù)應該如圖5中虛線所示。而圖3所示實際測量數(shù)據(jù)呈現(xiàn)明顯的正弦趨勢，證明實際測量過程中確實存在這種系統(tǒng)誤差，所以在測量中消除這種系統(tǒng)誤差才能得到準確的跳動量。

1.2.2 極坐標變換法消除誤差

按照以下步驟可從原理上消除端面傾斜引起的系統(tǒng)誤差。

1)根據(jù)伺服電動機帶動靜壓主軸的轉速和位移傳感器的采樣頻率，得到旋轉1周的總采樣點數(shù)N為

(4)

式中：n為主軸旋轉的速度，r/min；f為采樣頻率,Hz。

2)在實際測量中采集的信號數(shù)據(jù)點多于N，消除誤差時只需要一整個圓周的信號即可，所以截取整個圓周N個數(shù)據(jù)點進行極坐標變換，對于任意一點(tk,sk),k=1,2,…,N，tk為采集信號的點數(shù)，sk為傳感器的示數(shù)，將其從t-s坐標系變換到極坐標系

(5)

式中：θk,ρk為極坐標下的坐標值。

由于極坐標不好計算且難以建立數(shù)學圖像，而直角坐標系下求取跳動更加方便和直觀，因此再將其轉化到直角坐標系下，進行以下變換

(6)

式中：xk,yk為直角坐標系下橫、縱坐標值。

3)提取變換之后的數(shù)據(jù)點(xk,yk)進行最小二乘擬合圓，即

(7)

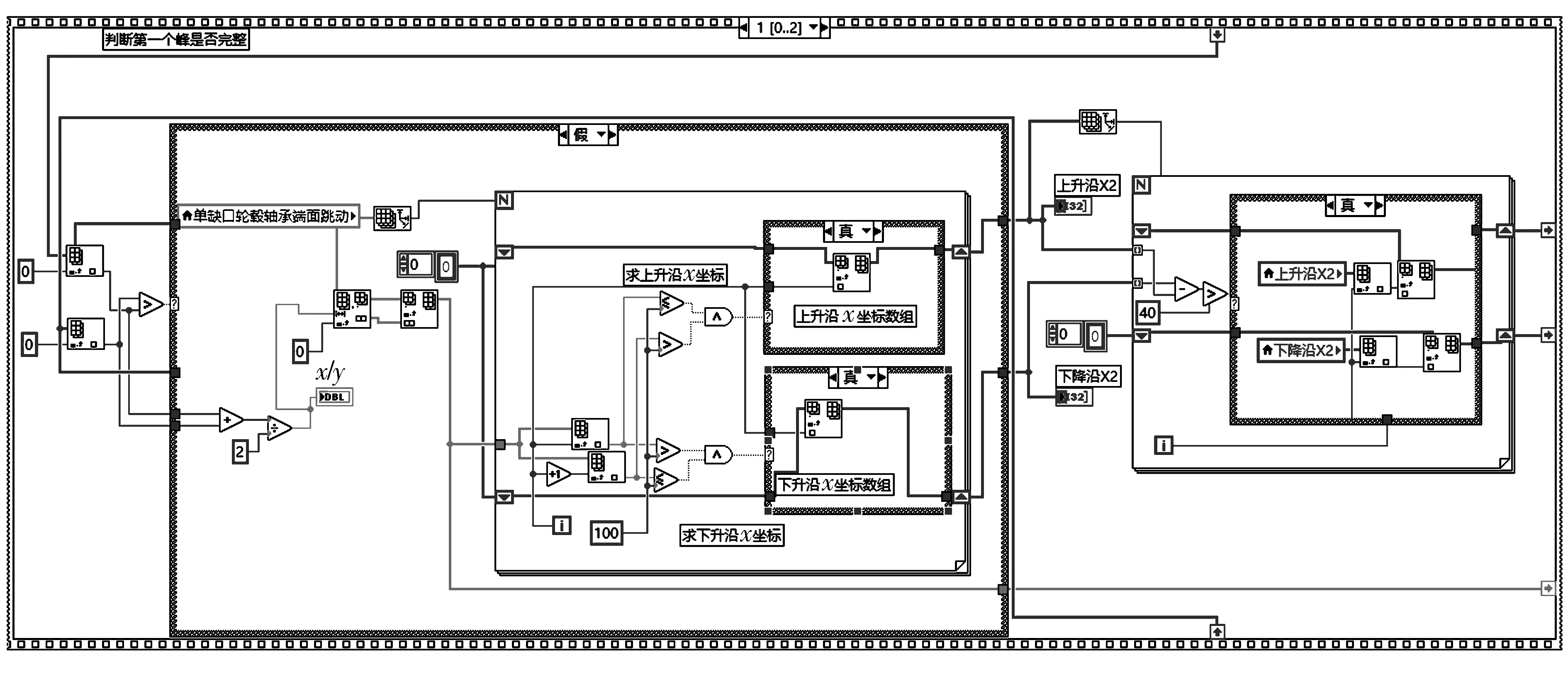
式中：f(x)為待擬合的方程；M為選取數(shù)據(jù)點的總數(shù)，對于連續(xù)端面M=N，對于離散端面M

f(x)的函數(shù)模型為(x+x0)2+(y+y0)2=r2，所以可以利用最小二乘擬合方法得到圓心O1的坐標(x0,y0)和半徑r，如圖7所示。擬合出來的半徑r實際上就是傾斜量δ。

圖7 擬合圓示意圖

4)對擬合后的任意點P(xj,yj)進行(5)式和(6)式的反變換得到P0(tj,sj),j=1,2,…,N。

則消除誤差后的數(shù)據(jù)為

Lk=sj-sk。

(8)

圖3中的數(shù)據(jù)經消除誤差后如圖8所示，對比可知：圖3中的原始信號有明顯的正弦趨勢，這種趨勢就是由于端面傾斜導致的系統(tǒng)誤差，在經過上述的方法消除誤差之后，這種趨勢被明顯消除。

圖8 輪轂軸承凸緣端面消除誤差后的跳動數(shù)據(jù)

1.2.3 端面跳動信號提取

由于輪轂軸承凸緣端面的形狀并不單一，所采集到的端面信號不能全部使用，需要對采集信號進行提取。將采集到的輪轂軸承凸緣端面信號分為連續(xù)端面跳動信號和離散端面跳動信號進行分析。

1)連續(xù)端面跳動信號提取

對于無缺口型輪轂軸承凸緣，采集到的是連續(xù)端面跳動信號，位移傳感器在整個測量過程中都與被測表面接觸，所以采集到N個數(shù)據(jù)點的信號都是準確可用的，消除誤差后的數(shù)據(jù)點sk如圖9所示，則連續(xù)輪轂軸承的端面最大跳動為

SC=max(Lk)-min(Lk)。

(9)

2)離散端面跳動信號提取

相對于無缺口型輪轂軸承凸緣采集到的連續(xù)端面信號，離散端面跳動信號復雜一些。由于凸緣端面有缺口，采集過程中位移傳感器在有缺口的地方沒有與端面接觸，會造成相應信號的缺失，如圖3b和圖3c所示。同時，當凸緣從缺口處旋轉到與位移傳感器接觸時，此過程產生的撞擊會極大地影響傳感器的采集精度。

SD=max(Lq)-min(Lq)。

(10)

圖10 離散端面跳動信號提取

2 試驗設計

基于上述測量原理進行輪轂軸承凸緣端面跳動測量試驗。試驗由2大部分組成：1)機械部分，利用伺服電動機,通過同步帶傳動帶動靜壓主軸旋轉實現(xiàn)被測軸承凸緣的旋轉，并固定傳感器；2)控制和信號采集系統(tǒng)，主要包括控制伺服電動機的轉動和輪轂軸承凸緣端面跳動信號的采集、轉換和處理，并得到最終的跳動量。

2.1 機械測量裝置

測量裝置如圖11所示,具體測量步驟如下：

1)將被測軸承置于放置臺，盡可能使被測軸承凸緣端面與放置平臺之間的安裝傾斜度為零，調節(jié)鎖緊螺母將被測軸承鎖緊。

2)將電感位移傳感器安裝好，旋轉調節(jié)螺母，使傳感器在整個回轉過程中保持在一半量程左右，同時不能與被測軸承發(fā)生干涉。

3)啟動油泵和工控機，使伺服電動機運轉，通過同步帶帶動靜壓主軸和被測軸承做同步勻速回轉運動。

4)等待被測軸承的回轉運動穩(wěn)定，運行LabVIEW采集程序，將傳感器所采集1個周期的端面跳動信號經過A/D轉換器傳輸?shù)接嬎銠C，在LabVIEW中經過數(shù)據(jù)處理顯示出測量結果。

1—同步帶；2—靜壓主軸；3—回轉軸；4—軸承放置平臺；5—被測輪轂軸承；6—總體機架；7—工控機；8—位移傳感器；9—傳感器鎖緊件；10—傳感器固定架；11—傳感器調節(jié)架；12—伺服電動機；13—電動機固定架

2.2 系統(tǒng)軟件設計

輪轂軸承凸緣端面跳動信號的采集采用虛擬儀器技術，利用LabVIEW編程實現(xiàn)數(shù)據(jù)采集、信號顯示、數(shù)據(jù)處理及存儲讀取等功能[6]。主要的子程序如圖12—圖14所示。

3 試驗結果

取3種型號的輪轂軸承各1套，進行10次裝夾，每次裝夾好測量1次凸緣端面跳動，測量結果見表1。由表可知，3套軸承各自的10次測量結果極差為±2 μm，相比采用手動千分表進行端面測量時6～7 μm的精度有很大提高，測量系統(tǒng)的重復性精度達到了預期要求。

圖12 端面跳動信號最小二乘擬合子程序圖

圖14 離散端面信號截取子程序圖

表1 輪轂軸承端面跳動試驗測量結果

4 結束語

介紹了一種基于LabVIEW的輪轂軸承凸緣端面跳動測量方法，利用極坐標和直角坐標變換消除了端面傾斜系統(tǒng)誤差。多次重復試驗數(shù)據(jù)證明此方法可以達到預期要求的測量精度。