基于Geogebra軟件的中職數學課堂設計

高芹

摘? ?要：文章從備課設計、課上設計與測試反饋設計3方面探究Geogebra在中職數學課堂教學設計中的應用，以期將軟件在中職數學教學中的作用更好地發揮出來，優化中職數學課堂設計及其教學效果。

關鍵詞：Geogebra軟件;中職數學;課堂教學設計

中職數學教學主要是對學生的基本數學能力進行培養，為學生今后的數學發展十分重要，教師需要在教學過程中做好課堂教學的設計工作，把握關鍵點，提高學生學習效率。但是長期以來，中職數學教學多強調知識的傳授與技能的訓練，課堂教學大多對灌輸式講授法予以采用，學生的學習通常是聽講、模仿、記憶并再現教師所授知識，屬于被動接受知識并強化存儲的過程。教學方法上的單一令學生對數學學習產生枯燥乏味之感，越學興趣越低。針對這種情況，文章試圖在中職數學課堂設計中對Geogebra軟件加以應用，讓更多中職數學教師及學生了解Geogebra的強大功能與易用性的同時，以該軟件為支持優化數學課程的教學效果，實現數學教學模式的轉變。

1? ? Geogebra軟件的特點與功能

1.1? Geogebra特點

Geogebra是一款結合幾何、代數與微積分的免費動態數學軟件，含直線、向量、曲線以及函數等基本元素在內，可通過便捷化的動態演示對軌跡的生成過程進行探索與顯示，將代數、幾何圖形內在關系的環境展示出來，令抽象而枯燥的數學內容變得具體、生動與形象[1]，特點如下：（1）功能強大，軟件集幾何作圖、數據運算與數據處理等于一體，在中職數學的教與學中十分適用，可省去多個軟件相互切換的工作。（2）易于交流與學習，軟件內含“作圖過程”及“作圖過程導航條”工具，能將教案的制作過程再現，做到“所見即所得”。（3）幾何屬性多樣化，軟件內置較多的幾何體屬性，包括圓錐曲線、極線、切線以及函數求導等內容，顏色亦有多樣化的呈現。（4）自定義工具屬性，在繪圖過程中，Geogebra提供制定的輸入與輸出物件，師生可在工具列上建立所需繪圖工具，Geogebra網站的wiki中還提供了豐富的圖案與工具以供使用。（5）免費共享，Geogebra以Java程序為基礎而編寫，可為遠程交流及網上學習提供便利[2]。

1.2? Geogebra功能

（1）快速而精確的作圖功能。Geogebra可快速、直接地作出很多基本圖形，如點、線、向量、多邊形、圓、角等，亦能直接在命令列中輸入代數表達式，獲取相應圖形，左邊代數區、命令列與繪圖區均能進行參數的修改，通過對數值精度的設置，滿足精確度要求。（2）實時動態的圖形變化功能。Geogebra的工具欄可快速而又動態地實現圖形的對稱、反演、平移以及縮放等功能，軟件左側代數區會以代數式的形式將圖形顯示出來，并隨著圖形的變化而動態改變，同時，動態跟蹤對象軌跡。（3）強大的測量與計算功能。Geogebra中的工具欄能對長度、角度、弧長以及封閉圖形的周長、面積等進行直接的測量，在左側代數區顯示運算結果。除了可以執行常見的四則運算、指數與對數運算、三角函數運算外，Geogebra的函數運算、科學計算以及統計與微積分功能亦很強大，讓師生的運用得心應手。（4）強大的動態函數與方程功能。Geogebra軟件可進行函數與方程圖像的邊界繪制，且將它們的生成過程動態地呈現出來。在繪圖區進行圖形的繪制之時，Geogebra代數區可動態顯示對應圖像的代數表達式，若在軟件命令欄中輸入某一點、向量、函數或方程，代數區與繪圖區還會同時顯示對應對象。無論對象發生怎樣的變化，該對象的全部表達方式均會實現動態的連接與調整，體現出很好的動態效果。

2? ? 應用Geogebra軟件設計中職數學課堂教學

狹義層面分析，中職數學課堂教學的設計應包括備課設計、課上設計以及測試反饋設計3大環節。分析其具體內容，備課設計包括撰寫與制作教案及課件;課上設計包括探究教學雙向互動以及數學實驗課等;測試反饋設計則對命制、批改、評講課堂練習及大中型測試試卷等各類題目予以涉及[3]。

在備課設計環節中，應主要利用Geogebra生成精確的教學圖形與圖像，將其在教案與課件中應用，這一點在進行平面幾何及幾何課程的講解之時尤為重要。教師應在精心構思中將各種動畫的演示與漸變效果體現出來，節約課上描點繪圖的時間，提高備課效率，獲取能夠媲美教材的教案及課件。課件庫與基本元庫的全校共享有利于教師備課及命題效率的提高。

在測試反饋設計環節，Geogebra的作用與備課設計環節大體一致。但有一點需要指出，隨著計算機硬件價格的普遍降低與各中職院校機房的普及，利用Geogebra開展數學課堂教學設計與實驗并以此為依據對學生的數學成績進行綜合評價可行性已很明顯。

課上設計環節是中職數學課堂教學設計的真正實施環節，亦是應用Geogebra的中心環節，應圍繞以下兩點進行重點設計。

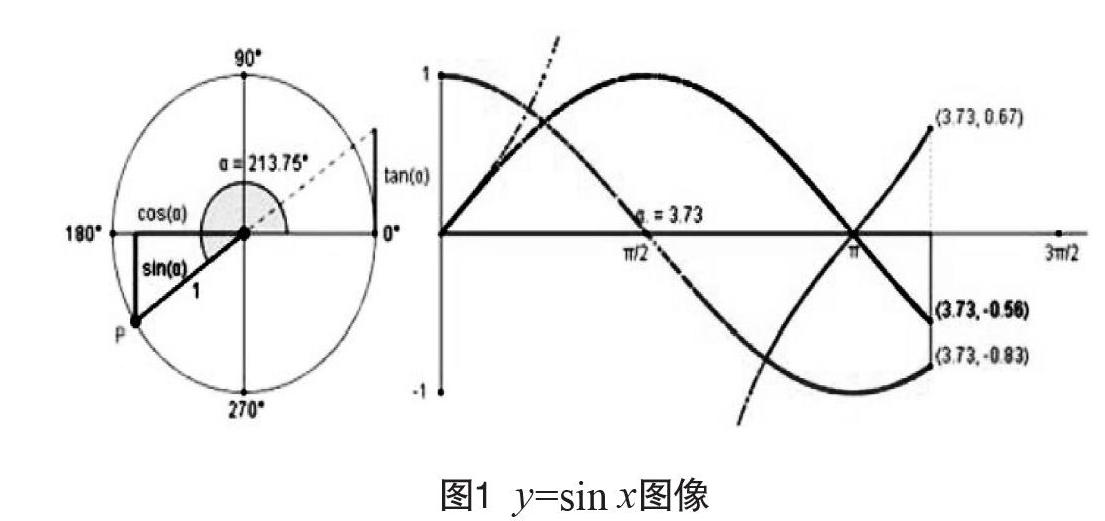
（1）通過對動畫演示漸變過程的制作，將諸多教師講解難、學生理解難的內容動態展示出來。例如，利用單位圓進行y=sin x圖像的繪制，如圖1所示，通過直接的拖動以及對坐標軸比例的變化，可將y=sin x圖像向的漸變過程生動地演示出來。

（2）通過數學實驗課（一人一機），開展探究性活動，對學生的動手能力與自主學習能力以及細心、不怕困難的思維品質進行培養。學生是實驗課程的真正探索主體，教師在其中發揮組織者、指導者與問題初步提出者的作用。課上設計工作應做到讓學生根據教師提出的初步問題進行逐步的分化、細化與求精，借助Geogebra的強大圖形及代數功能尋找相應問題的具體解決思路與方案，同時，在探索中提出新問題。

例如，讓學生利用平面幾何方法對三角形“五心”向量表示的正確性進行驗證。

已知采用向量運算的方法輸入（A+B+C）/3便可在幾何區將ΔABC的重心點直接顯示出來。實際上，借助角度的正余弦計算以及向量運算能夠給出“五心”的向量表示。于是通過平面幾何方法做出三角形的“五心”并與之對比，可以發現兩者是重合的，這意味著向量表示具有正確性。此處學生可在Geogebra作圖區的任意位置繪制三角形，并對其進行隨意的拉動。

下面的公式為在Geogebra命令框內輸入以下兩命令之后的結果：

又如，在實驗中，通過對圓的半徑以及圓心到直線的距離的改變，讓學生在最短的時間內進入情景，對r，d對直線及圓位置的影響有一個直觀的感受。可通過設計以下問題來完成：已知直線l∶3x-y-6=0與圓心為C的圓x2+y2-2x-4y=0，對直線l與圓的位置關系進行判斷，若相交，求取它們交點的坐標。

已知直線與圓的位置關系包括相離、相切與相交3種，各關系交點的個數分別為0個、1個與2個。根據所學知識圖像的變化可知，若圓心與直線之間的距離d比圓的半徑r大，則兩者之間是相離的。若d=r，兩者相切;而若d

圖2? 直線和圓的位置關系

3? ? 結語

相較于當前流行的幾何畫板而言，Geogebra軟件所具有的功能更強，易用性更加突出，應在中職數學課堂設計及其教學中得到廣泛的應用。在Geogebra穿針引線的作用之下，中職數學的課堂教學各個環節可實現有效的整合，它對中職數學課堂設計及教學效果的優化是顯著的。

[參考文獻]

[1]沈翔.GeoGebra基本操作指南[M].北京：高等教育出版社，2016.

[2]靳菲菲，侯艷.GeoGebra軟件對中學數學課堂的影響[J].科協論壇（下半月），2012（1）：180-181.

[3]徐炳林，劉淑艷.GeoGebra在數學教學中的應用[J].中學數學研究（華南師范大學版），2013（13）：23-24.

Abstract：This paper makes a research on the application of Geogebra in secondary mathematics teaching design from prepare lessons， in class and test feedback 3 aspects， hoping that can play the softwares role preferably， and optimize secondary mathematics teaching design result.

Key words：Geogebra software; secondary mathematics; teaching design