螺旋槳附連水效應的數值計算方法研究

吳 帥 ， 林 焰 ， 吳文偉

（1.大連理工大學 船舶CAD工程中心，遼寧 大連116024；2.中國船舶科學研究中心，江蘇 無錫214082）

0 引 言

螺旋槳在流體中振動時，流體會反作用于螺旋槳，從而使槳產生軸向加速度和周向角加速度，會導致形成縱向附連水質量和附連水轉動慣量（極轉動慣量）。其中，在船舶推進軸系的振動和校中分析計算中，這兩個參數的計算正確與否，會直接影響軸系振動固有特性分析的準確程度[1-4]。所以，準確計算螺旋槳的附連水質量和轉動慣量，成為分析軸系振動特性的關鍵一環。

目前，對螺旋槳附連水效應的研究，國外進行的試驗和理論研究比較多。對于縱向附連水質量，一般分為槳轉動和停止兩種情況，國內基本利用國外的經驗公式和經驗系數來進行附連水效應的估算。Burrill等[5]做了大量螺旋槳模型試驗，推導了縱向平動附加質量公式和相配的公式經驗系數；Schwanecke[6]推導了商船的螺旋槳附連水轉動慣量計算公式；Brooks[7]通過理論方法和試驗研究了螺旋槳軸向振動的附連水質量；Parsons等[8]用專門的升力線和升力面理論對B系列槳的數值計算進行了統計分析，得到了螺旋槳軸向附連水質量和附連水轉動慣量的計算公式和相應的公式系數；Harrington[9]基于槳的葉厚和葉寬建立了螺旋槳重量的計算公式，并用于槳附連水效應的估算；Donald等[10]對以往螺旋槳附連水效應的估算方法進行了概述性分析，并在Burrill估算公式的基礎上進行了改進，并跟Burrill的試驗結果數據進行了對比，具有很好的匹配性；Korotkin[11]對船舶結構的附連水質量進行了研究，對螺旋槳的附加質量進行了理論推導，討論了確定螺旋槳附加質量的方法；Hutchison等[12]研究了導管螺旋槳的附加質量計算；鄒冬林等[13]用面元法研究了船舶螺旋槳的附連水質量與阻尼；中國船級社CCS[14]規定了螺旋槳附連水效應考慮的經驗系數。

對于螺旋槳的附連水效應分析，由于試驗成本很高，所以采用數值模擬顯得非常重要。本文通過Catia實現了螺旋槳的三維建模，利用Abaqus有限元分析軟件進行了螺旋槳附連水轉動慣量（極轉動慣量）和縱向附連水質量的分析，同時利用多個經驗公式進行了估算，將仿真和估算結果進行了對比和分析。

1 螺旋槳附連水效應分析

式中：M為整個系統質量（包含螺旋槳及其附連水質量）；x¨為螺旋槳的振動加速度；F0為激振力大小；M0為螺旋槳質量（或者真空中的質量）；m為螺旋槳的附連水質量。

由該理論可以知道，只需要計算出真空中和水中兩種情況下的頻率響應，針對某一頻率處的加速度，求出對應的質量，取差值就可以得到附連水質量。如果將質量替換為轉動慣量，激振力替換為激振扭矩，則同樣可以計算附連水轉動慣量，此處不再通過公式重復敘述。

將結構部分和流體部分均利用有限元法離散，從而建立并利用諧響應穩態分析法求解流體和固體耦合的振動方程，對整個系統施加一個外部激振力，從而將整個系統簡化為一個單自由度強迫振動系統[14]：

該種激勵情況，振動中振幅非常小，導致阻尼C和位移x的值也很小，可以忽略不計，那么振動方程可以簡化為：

考慮附連水效應的整個系統質量：

2 螺旋槳附連水效應計算經驗公式

（1）Parsons[8]基于升力線、升力面等理論，對B系列螺旋槳進行了數值計算和統計分析，提出了計算經驗公式：

式中：因子CIE和CWER的計算公式為

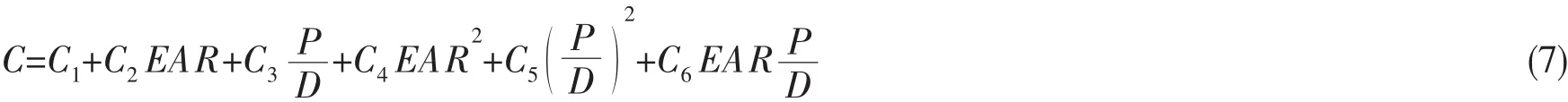
上面公式中的系數取值如表1和表2所示。

表1 Parsons公式CIE計算經驗系數Tab.1 Empirical coefficients of CIEin Parsons formula

表2 Parsons公式CWER計算經驗系數Tab.2 Empirical coefficients of CWERin Parsons formula

升力面修正系數LSC的計算公式：

式中：IE為附連水轉動慣量，kg·m2；WEL為縱向附連水質量，kg；D為螺旋槳直徑，m；ρ為水的密度，kg/m3；為螺距比；EAR為盤面比。

描述槳葉幾何特征的比率AR：

（2）Donald等[10]考慮到Burrill的評估公式在許多情況下計算螺旋槳的附連水效應時不夠精確，對其公式進行了改善，系數取值如表3和表4所示。附連水轉動慣量IE：

軸向附連水質量WEL（槳停車狀態）：

表3 Donald/Burrill公式CIE計算系數Tab.3 Empirical coefficients of CIEin Donald/Burrill formula

表4 Donald/Burrill公式CWEL計算系數Tab.4 Empirical coefficients of CWELin Donald/Burrill formula

可以通過一個新的關系來修正螺旋槳從“停車”（locked）到“旋轉”（rotation）的附連水質量。該修正因子可以由下面公式得到：

（3）Schwanecke[6]提出了用于商船螺旋槳附連水轉動慣量評估的公式。

附連水轉動慣量IE：

3 螺旋槳及槳水耦合有限元模型

本文采用的螺旋槳模型為某多用途船的螺旋槳設計，其主要設計參數和材料屬性如表5所示。

表5螺旋槳設計參數及材料屬性Tab.5 Design parameters and material property of propeller

根據螺旋槳的參數，利用張宏偉[16]的螺旋槳三維坐標轉換公式，可以推導出槳的三維坐標，利用Catia建立螺旋槳的三維幾何模型，導入Abaqus后，進而建立槳、水域的三維模型，最后劃分網格完成螺旋槳有限元模型、槳-水耦合有限元模型，如圖1-4所示。為降低邊界對計算的影響，水域模型的半徑大約為槳模型半徑的6倍，水域外部邊界條件設定為無反射邊界；內部跟槳轂接觸部分，由于槳旋轉和軸向振動過程中槳轂引起的附連水效應微小，所以不考慮槳轂外形引起的附連水效應，即無需對槳轂與水建立相互作用。同時，為了模擬水在槳轂表面的邊界條件，將該槳轂表面可形成的圓柱形設定為固定邊界，作為水域內邊界，來模擬水不能越過槳轂。但是為了方便在槳葉上施加作用力和真實模擬整個槳體，仍需要建立槳轂模型，通過建立參考點與槳轂內表面耦合，在參考點上施加激勵載荷可以得到槳的振動響應；內部跟槳葉接觸部分，由于槳附連水效應主要由葉片導致，所以通過將葉面和接觸水綁定來模擬實際情況。為了滿足計算精度和降低成本，水域模型采用內細外粗，槳葉接觸水兩部分，劃分的網格大小相同。水域采用了聲學四面體單元AC3D10，螺旋槳采用實體四面體單元C3D10。利用Abaqus的模型分析功能，可以得到螺旋槳的質量和轉動慣量分別為11 190 kg和14 000 kg·m2，圖紙提供的槳質量和轉動慣量分別為11 560 kg和14 110 kg·m2，誤差大小分別為3%和0.7%，在5%以內滿足分析要求，可以利用此模型進行螺旋槳附連水效應的分析計算。螺旋槳有限元模型由18 389個C3D10單元構成，水域由167 743個AC3D10單元構成。

圖1螺旋槳三維幾何模型Fig.1 3D model of the propeller

圖2螺旋槳有限元模型Fig.2 Finite model of the propeller

圖3槳水耦合三維幾何模型 Fig.3 3D model of the propeller-water coupling

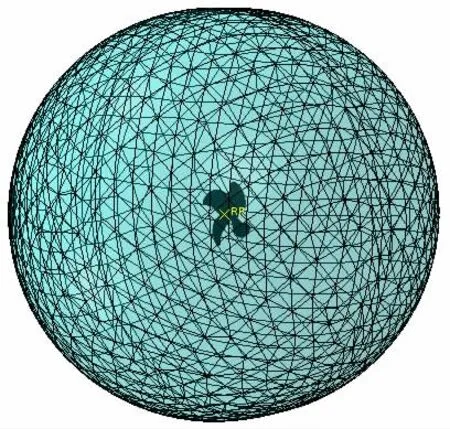
圖4槳水耦合有限元模型Fig.4 Finite model of the propeller-water coupling

4 螺旋槳附連水效應的計算分析

4.1 附連水轉動慣量的計算分析

為了施加激振載荷，在槳轂的內表面中心處，建立一個與槳轂內表面耦合的參考點，這樣可以在該點處施加繞槳軸的激勵扭矩。計算時，空氣中和水中對螺旋槳的激勵扭矩均設定為 10 000 N·mm，激勵頻率為 1～80 Hz。通過頻率響應計算，可以計算出螺旋槳耦合前后在各個頻率處的加速度。當螺旋槳在遠離共振頻率的頻率段時，就可以通過比較參考點處耦合前后的某頻率處的加速度，計算出該頻率下的附連水質量。考慮到共振頻率附近，由于失真很大，會導致該方法失效，所以盡可以遠離共振區選擇低頻區的頻率點。另一方面，螺旋槳處的自身激勵頻率主要為葉片次激勵頻率。根據本文中螺旋槳的額定轉速，可以計算出激勵頻率為9.733 Hz，仿真中均為整點頻率，所以選擇10 Hz來進行對比分析。真空中和水中的頻率響應分析結果如圖5和圖6所示。可以看出由于水的耦合作用，導致螺旋槳的共振頻率點降低，即固有頻率降低，符合實際的振動情況。

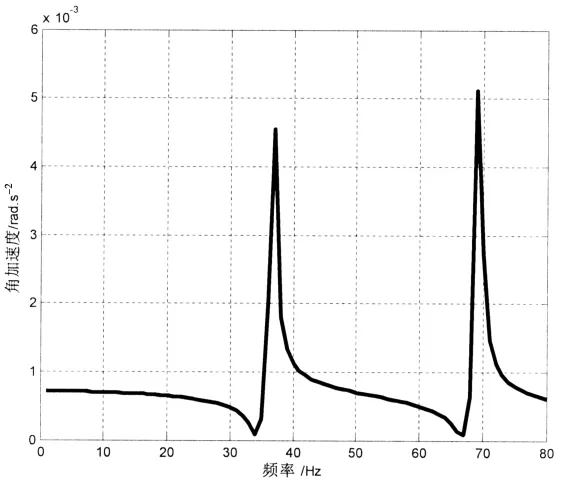
圖5真空中參考點角加速度響應曲線Fig.5 Angular acceleration response curve of reference point in vacuum

利用兩種情況下10 Hz頻率點處的角加速度，結合激勵扭矩，可算出轉動慣量。根據兩個結果的差值，得到附加轉動慣量，并跟Abaqus分析得到的槳轉動慣量對比，得到相對系數，如表6所示。

利用前面介紹的經驗公式進行螺旋槳附加轉動慣量的估算，同仿真結果進行對比，結果對比如表7所示。相對系數為附加轉動慣量與真空中槳慣量的比值，整體系數為水中槳轉動慣量和真空中槳慣量的比值，相差百分比以計算的最小結果為基準，即Donald/Burrill的計算結果。

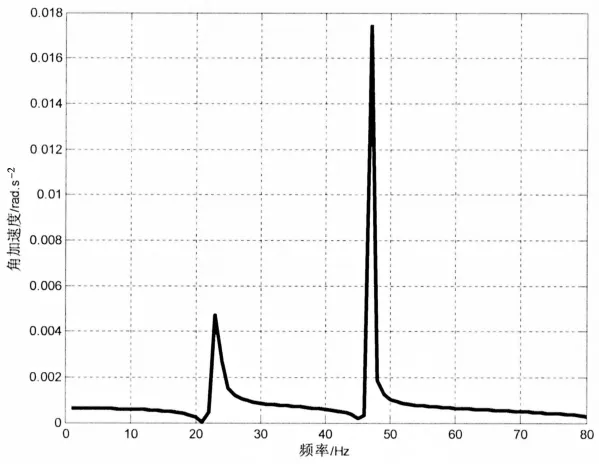
圖6水中參考點角加速度響應曲線Fig.6 Angular acceleration response curve of reference point in water

表6 Abaqus仿真得到附加轉動慣量Tab.6 Added inertia obtained in Abaqus

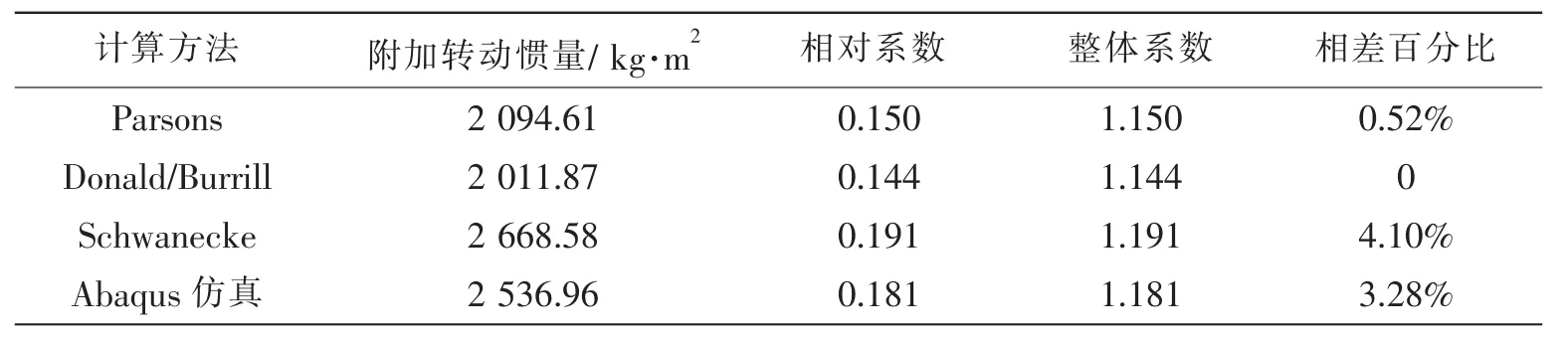
表7四種計算方法結果對比Tab.7 Comparison of the results of the four methods

通過上表可以看出，Abaqus計算結果處于經驗公式計算范圍內，而且相差百分比為3.28%，在5%以內，相對來說比較合理。

4.2 縱向附連水質量的計算分析

考慮到軟件的計算能力有限，本文只分析螺旋槳“停車”（locked）狀態下的縱向附連水質量。針對此種情況，同樣在參考點處施加軸向激勵載荷。計算時，空氣中和水中對螺旋槳的激勵力均設定為x軸向力10 N，激勵頻率為1～80 Hz，跟前面附連水轉動慣量的分析類似，選擇10 Hz來進行對比分析。真空中和水中的頻率響應分析結果如圖7和圖8所示，同樣可以看出由于水的耦合作用，導致螺旋槳的縱向共振頻率點降低，即固有頻率降低，符合實際情況。

利用兩種情況下10 Hz頻率點處的加速度，結合激勵力可算出質量，根據兩個結果的差值，得到附加質量，并與Abaqus分析得到的槳質量對比，得到相對系數，如表8所示。

同樣，利用前面介紹的經驗公式進行螺旋槳附加質量的估算，rotation和locked這兩種狀態都用計算公式計算，同仿真結果進行對比，結果對比如表9所示。相對系數為附加質量與真空中槳質量的比值，整體系數為水中槳質量和真空中槳質量的比值，相差百分比分別在兩種狀態下（rotation和locked）以計算的最小結果為基準。

圖7真空中參考點加速度響應曲線Fig.7 Acceleration response curve of reference point in vacuum

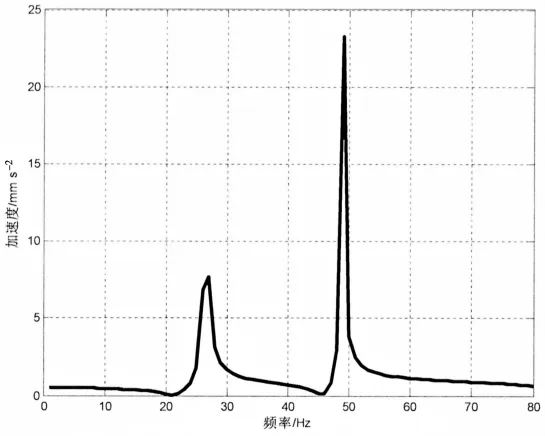
圖8水中參考點加速度響應曲線Fig.8 Acceleration response curve of reference point in water

表8 Abaqus仿真得到附加質量Tab.8 Added mass obtained in Abaqus

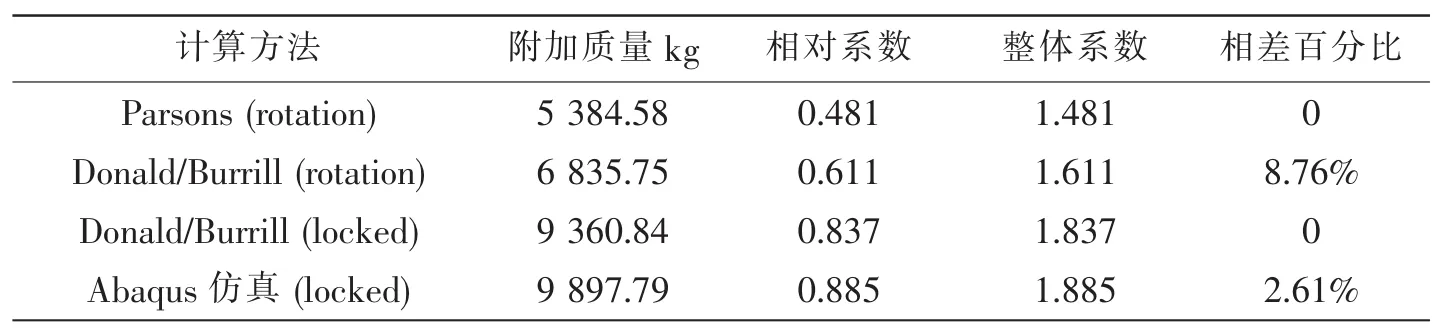
表9各計算方法結果對比表Tab.9 Comparison of the results of the different methods

通過上表可看出，Abaqus結果與Donald/Burrill（locked）很接近，相差百分比為2.61%，在5%以內，比較合理；還可看出Parsons（rotation）和Donald/Burrill（rotation）計算結果有些偏差，而且可以得到“旋轉”狀態下的附連水質量小于“停車”狀態下的結論。

5 結 論

本文通過對螺旋槳的附連水效應進行仿真計算，并跟經驗公式的計算結果進行對比分析，可以得到如下結論：

利用諧響應穩態計算方法對螺旋槳進行頻率響應分析，選取低頻區的非共振頻率點，可以計算出螺旋槳的附連水轉動慣量（極轉動慣量）和縱向附連水質量。通過跟經驗公式計算結果對比分析，可以得到，數值仿真和經驗公式結果誤差在5%以內，滿足計算要求；而且，還得到螺旋槳在旋轉情況下縱向附連水質量比停止情況小的結論。因此，在對螺旋槳的附連水效應數值精度要求高的情況下，可以利用該方法進行計算。