動量輪微振動機理及仿真

馬艷紅，劉珊珊，王虹，洪杰，*

（1.北京航空航天大學 能源與動力工程學院，北京100083； 2.先進航空發動機協同創新中心，北京100083；3.北京控制工程研究所 精密轉動和傳動機構長壽命技術北京市重點實驗室，北京100094）

動量輪作為衛星等航天器的重要定位、儲能、控制等功用的轉動部件，在軌高速旋轉工作時由于結構系統的幾何尺寸和力學特征的微小變化會引起多種振動激勵，使振動輸出載荷中包含寬頻微幅振動，從而誘發衛星系統低振動能量級的擾動（即微振動），雖然對航天器結構不會產生明顯損傷，但會嚴重影響衛星上高精度儀器的分辨率，限制衛星指向精度和姿態穩定度性能的不斷提高[1]，是影響高性能航天器指向精度和成像質量的重要指標。

微振動的表現特征為幅值小（0.01g量級）、頻率成分豐富（多倍頻）、頻帶寬（1～1 000 Hz）、存在行波振動。近年來，航天器平臺對指向精度和姿態穩定度要求不斷提升，指向精度要求達到0.01°，甚至角秒級，姿態穩定度達到10-3～10-4（°）/s，甚至10-5（°）/s量級。因此，動量輪的微振動問題愈發凸顯，嚴重制約了中國新研高精度衛星的發展。

國內外關于動量輪微振動機理的相關研究始于20世紀70年代，主要包括2個方面。一種是基于試驗結果反向建立的動量輪擾動模型。Hasha[2]將擾動擬合為一系列與動量輪轉速平方成正比的離散諧振，根據試驗結果確定經驗模型的系數，但由于未考慮慣性力矩對轉子結構的作用以及軸承擾振作用，使得部分高階的諧波響應明顯低于試驗結果。Masterson[3]基于此模型，推導動量輪不平衡量與擾動的關系，并采用彈簧-阻尼線性模型，建立了基頻諧振解析模型，但無法解釋響應中出現反進動的原因。Liu等[4]將寬頻噪聲引入擾動，根據試驗不斷校正，才較好地解釋了動量輪低速運轉時振動模態及正反進動現象，但對于動量輪系統本身的激勵原理尚不清晰，導致高頻、高階的響應現象無法解釋。另一種是基于激勵種類正向建立的轉子動力學方程。Kim[5]研究了冷熱交變等外部激勵對動量輪的擾動作用，但忽略了內部的旋轉激勵，缺乏試驗數據支撐。周偉勇[6]基于線性假設建立了動量輪振動方程，僅考慮了輪體的靜不平衡量，并未將動不平衡、陀螺效應及軸承碾壓作用等因素引入方程中進行微振動性能預測，只獲得了基頻諧波的振動幅值。李連軍和戴金海[7]提出轉子系統內部存在摩擦、彈性振動及質量分布不均等激勵作用，但仍采用Jeffcott轉子模型理論推導并建立相關仿真模型分析時域內的振動響應，未能很好地與試驗相吻合。羅睿智等[8]分析了軸承滾動面幾何誤差的非線性接觸引起的預緊力波動，據此得到的數值解與高階振動瀑布圖符合得很好，但缺少動量輪自身結構特征引起激勵的機理分析。可見，由于微振動振源及激勵模式的不清楚導致始終未能建立精細的動量輪振動模型與試驗相互對照。

綜上可知，現有研究多將動量輪結構系統看作簡化對稱的穩定結構，研究不平衡量等激勵作用下轉子的振動響應，較少關注動量輪在工作過程中自身結構特征的微小變化及其引起的激勵作用。而這些正是動量輪擾振機理研究的核心問題，不能忽略或簡化，綜合考慮這些影響因素才能有針對性地開展動量輪微振動抑制技術研究。本文建立動量輪結構系統動力學模型，考慮支承不對稱的影響，重點研究動量輪幾何構形的非均勻性引起的微變形、輪緣的局部微振動導致的結構參數激勵、支點動載荷形成的基頻激勵和軸承碾壓形成的高頻載荷激勵，并通過仿真和試驗結合進行驗證。

1 旋轉態動量輪擾振機理分析

動量輪的結構系統示意圖如圖1所示。不考慮電機等驅動裝置，動量輪結構系統包括輪體結構、軸承支承結構、支桿結構與殼體安裝座結構四大部分。輪體結構本身為輪緣-輪輻的形式，在幾何構形上具有突變的結構特征，使輪體結構質量/剛度分布具有非均勻性。軸承支承結構為外環旋轉、內環固定的兩對角接觸球軸承，經過軸承滾子順序碾壓作用，將振動能量以高次諧波傳遞給支桿結構。支桿結構通過單端懸臂支承方式固定在殼體安裝座結構上，并通過安裝座與衛星星體相連。

為了分析動量輪結構系統在高速狀態下的擾振源，利用達朗貝爾原理可以得到多自由度、有阻尼系統的動力學方程為

式中：q為廣義坐標；M 為質量矩陣；C為阻尼矩陣；K為剛度矩陣；Q為系統廣義外力。

對于一般的機械振動系統，主要是研究廣義外力Q的變化引起的振動響應變化。在無外部激勵的情況下，廣義外力主要來自不平衡量。對于動量輪結構系統，雖經過精密的高轉速動平衡，但在工作時依然存在微振動。這就說明除了不平衡量的影響外，還存在其他的影響因素，即本文關心的重點為：一方面質量、阻尼和剛度這3個矩陣都是與動量輪自身結構特征有關的參數，在旋轉作用下發生的微小變化都會作為激勵，其中質量矩陣M 的變化主要來源于轉動慣量Ji各項；另一方面Q包括系統慣性載荷引起的支點動載荷及軸承碾壓作用下的高頻諧波激勵。

建立動量輪結構系統動力學模型如圖2所示。將動量輪結構簡化為輪緣-輪輻形式的輪體，軸承簡化為2對徑向剛度不同的線性彈簧單元，計及其阻尼作用。考慮到支桿結構由于單端懸臂支承方式引起的質量/剛度不對稱，利用有限元素法將結構系統離散成3個子域（即支桿段1、輪體段和支桿段2），圖2中每2個標記節點間為同一子域。

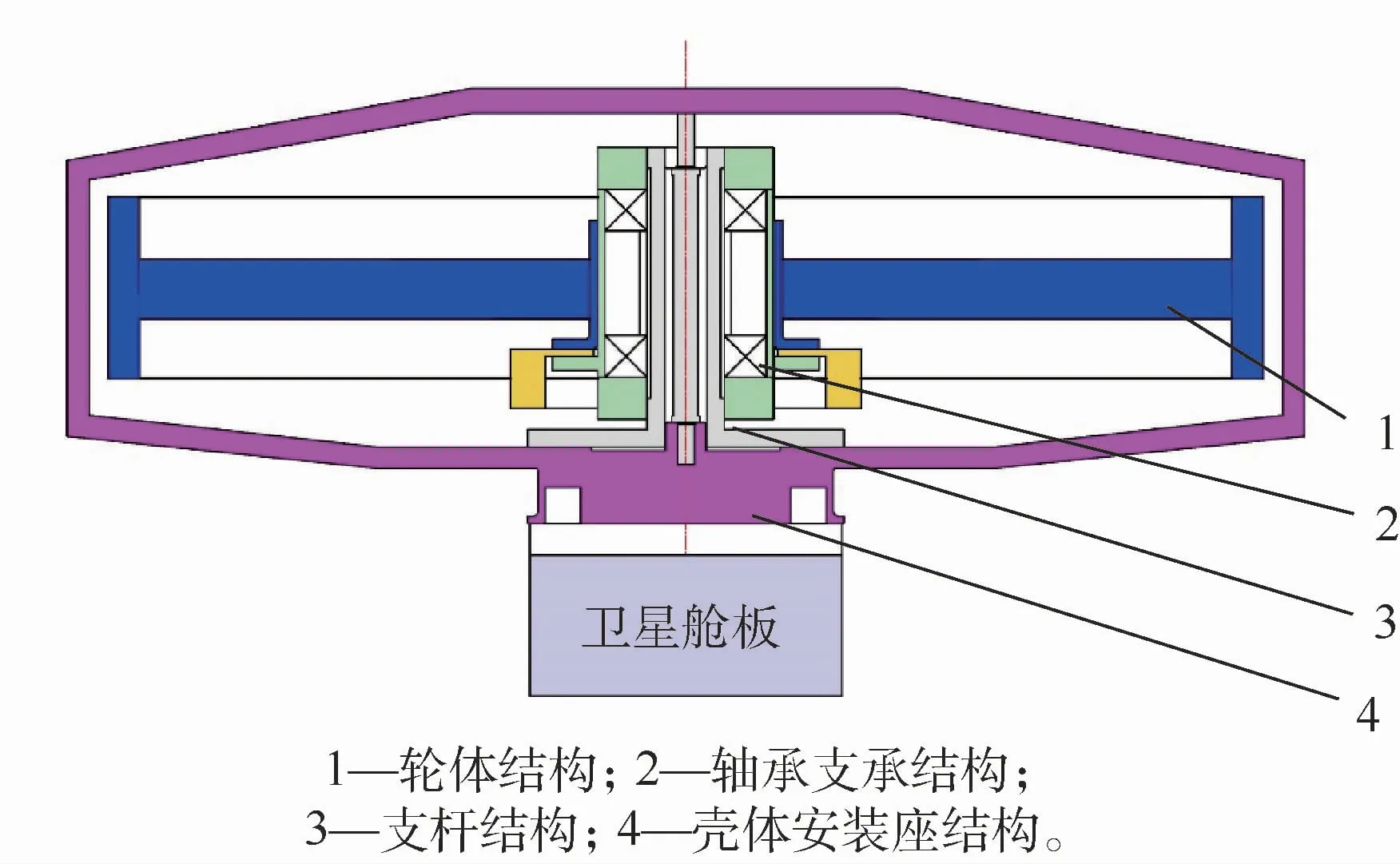
圖1 動量輪結構系統示意圖Fig.1 Structural system schematic diagram of momentum wheel

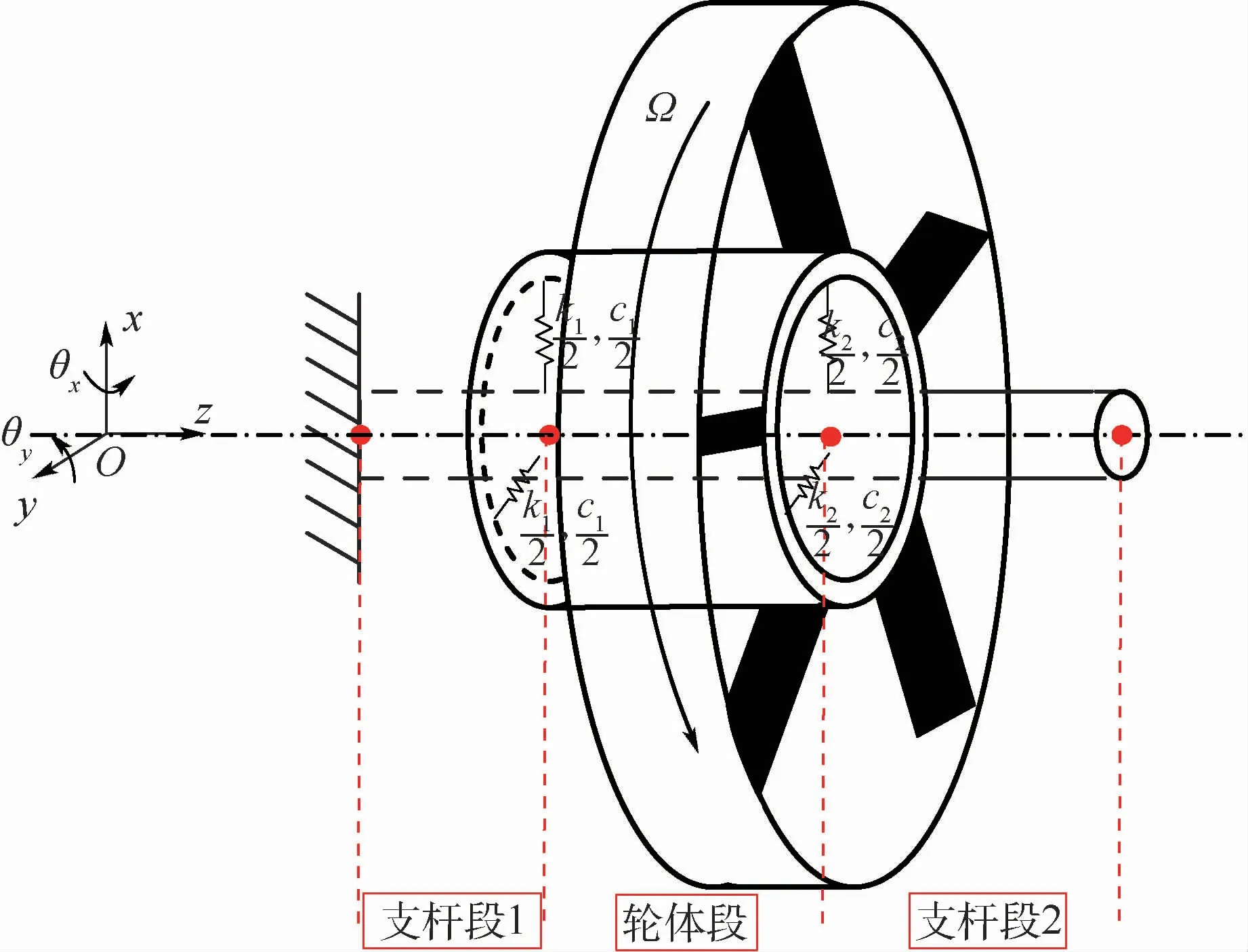
圖2 動量輪結構系統動力學模型Fig.2 Structural system dynamic model of momentum wheel

根據精度各子域內部可取有限多個節點。系統廣義坐標q表示各節點的5個自由度：位移x、y、z和轉角 θx、θy。

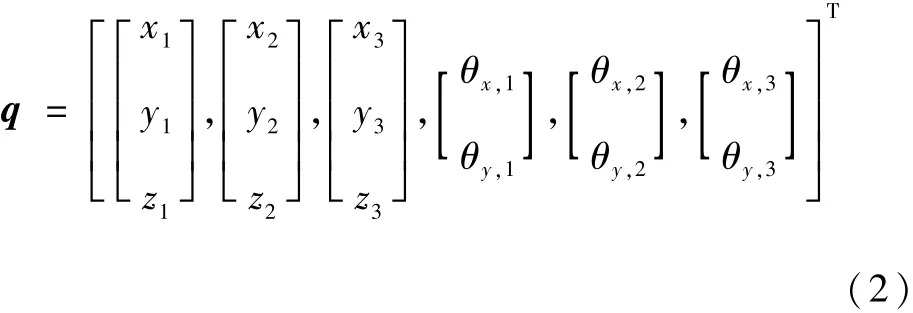
式（1）中的質量矩陣M 的表達式為

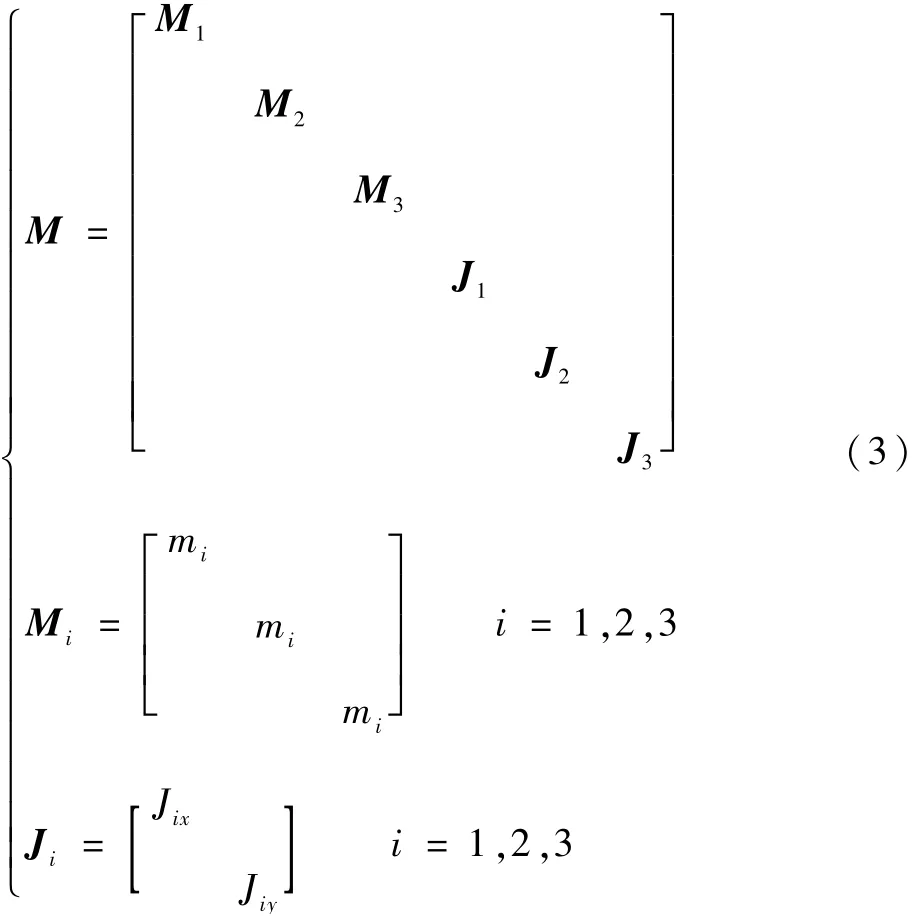
式中：Mi為第i個子域的平動質量矩陣；Ji為轉動慣量矩陣；mi為第i個子域的結構質量；Jix和Jiy分別為結構繞x軸和y軸的直徑轉動慣量；J2為輪體結構的轉動慣量矩陣，在高速旋轉狀態下其微小擾動構成了參數激勵的主要部分。

1.1 輪體結構的參數激勵

輪體結構144°剖視圖如圖3所示，其幾何特征為采用大直徑輪緣-輪輻組合結構，通過底部安裝邊與軸承支承結構連接，力學特征表現為轉動慣量大，但輪輻質量及其對輪緣的約束剛度沿周向具有非均勻性，在高速旋轉狀態下的局部振動作用下，會造成轉動慣量的非均勻性和分散性，進而作為參數激勵，引起系統的微振動。

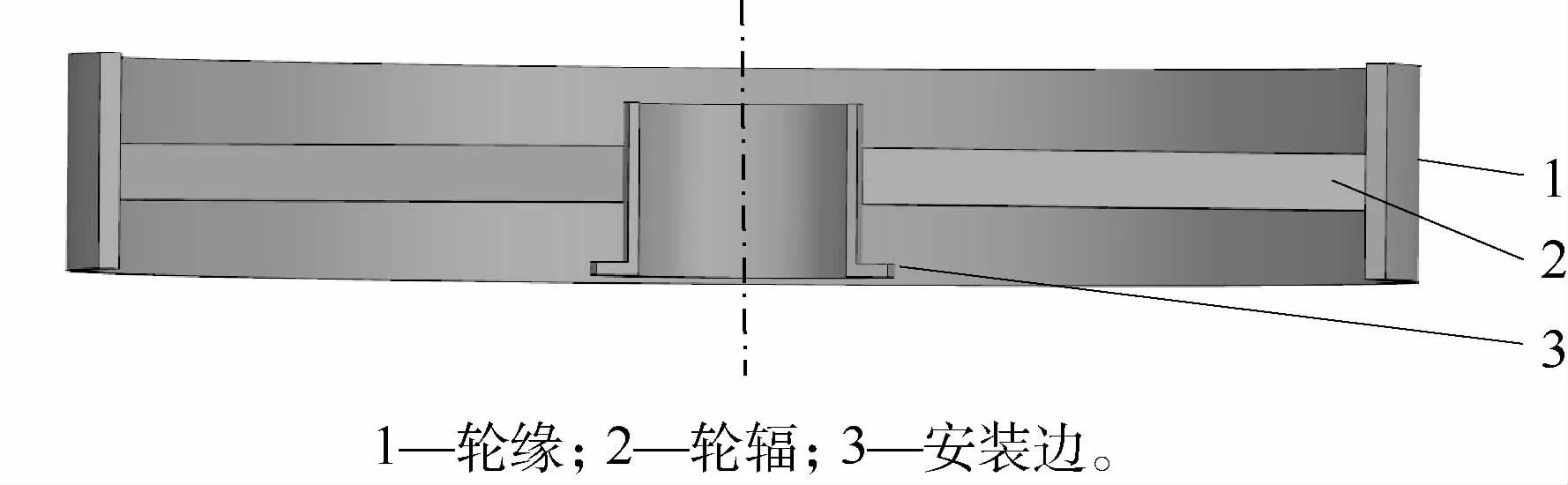
圖3 輪體結構144°剖視圖Fig.3 144°section view of wheel body structure

1.1.1 質量分布非均勻的影響

轉動慣量是轉動體繞轉軸旋轉時質量慣性的量度，包括直徑轉動慣量Jx、Jy和極轉動慣量Jz。由于輪體幾何結構非均勻，導致質量的非均勻分布，如圖4所示，用簡化二維截面計算輪緣-輪輻的直徑轉動慣量。選取與輪體底部安裝邊中心固連直角坐標系Oxyz，設第1條輪輻與x軸的夾角為θ1。則轉動慣量表達式為

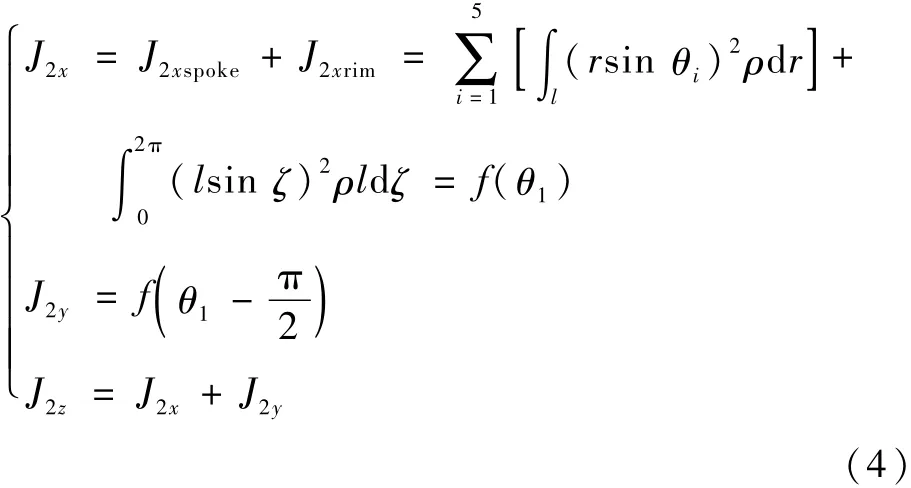
式中：l為輪緣半徑；ρ為材料密度；θi分別代表5條輪輻與x軸的夾角；r為輪輻微元體所在半徑長度；ζ為輪緣微元體與x軸的夾角。

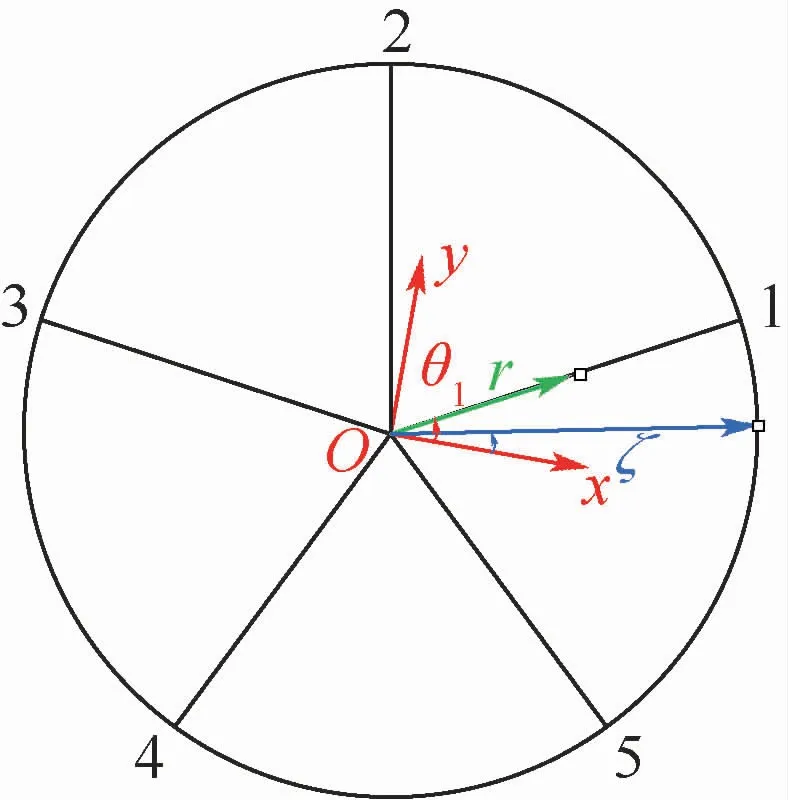
圖4 轉動慣量計算圖Fig.4 Moment of inertia calculation diagram

化簡式（4），得到

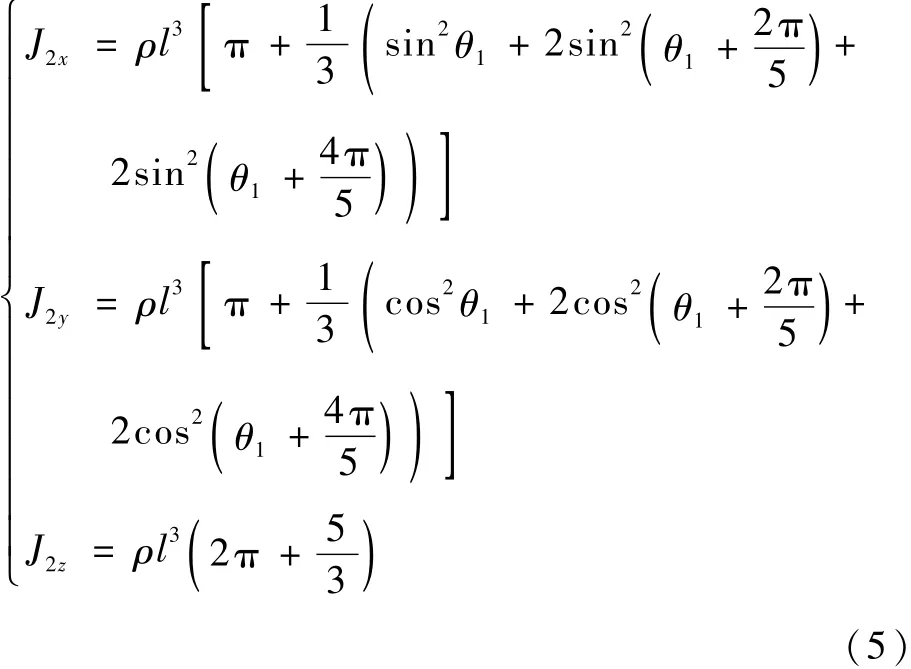
可見，J2x和J2y是 θ1的函數，而J2z與 θ1無關，是一定值，只有當存在不平衡量時會發生變化。對J2x求導（J2y等價），得到

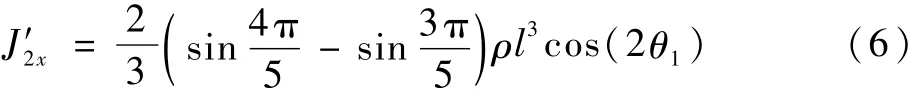
根據式（6），J2x的周期是 π，且當時，J2x取極值。此時的x軸和y軸即為慣性主軸。繪制無量綱J2x隨 θ1（0～360°）變化的關系，如圖5所示。隨角度的不同，任意時刻的直徑轉動慣量呈周期性變化，即質量矩陣M 一項中的J2x和J2y項在工作過程中具有非均勻性。

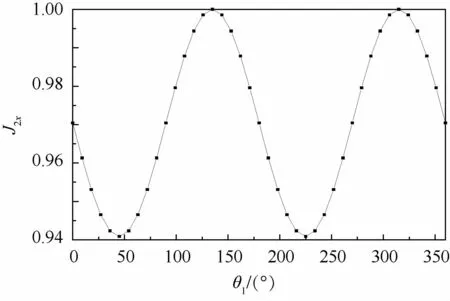
圖5 無量綱直徑轉動慣量J2x分布Fig.5 Dimensionless diameter moment of inertia J distribution

1.1.2 剛度分布非均勻的影響

高速旋轉狀態下，輪緣和輪輻的主要受力形式是離心拉應力，而剛度是抵抗變形的能力，由于二者沿徑向所受的拉力和剛度不同，使其變形不協調，相互約束。這種非均勻的微變形會使轉動慣量發生微變化。

輪輻各微元體所受離心拉應力大小與直徑成正比；輪緣厚度小、半徑近似為一定值，微元體所受離心力也為一定值。就剛度而言，以輪緣為研究對象，逐漸靠近輪輻連接處的約束剛度逐漸增大，而從輪緣微元體逐漸遠離輪輻的旋轉過程中，剛度逐漸減小。以輪緣微元體與輪輻中心線夾角為自變量建立極坐標系，如圖6所示。繪制輪緣無量綱徑向剛度的變化示意圖，如圖7所示。可見，徑向剛度呈周期性變化，周期為0.4π（約72°），在 θ=0.2 kπ處取極大值。

輪體旋轉狀態變形放大示意圖如圖8所示，線條對應轉速為零時的狀態，輪輻變形程度與直徑成正比，而輪緣的徑向變形由于受輪輻連接剛度的限制，使得沿周向觀察時的變形程度非均勻，這種變形狀態下的轉動慣量J2x會存在微小擾動 ΔJ2x，是與轉速有關的函數，即 ΔJ2x（Ω）。

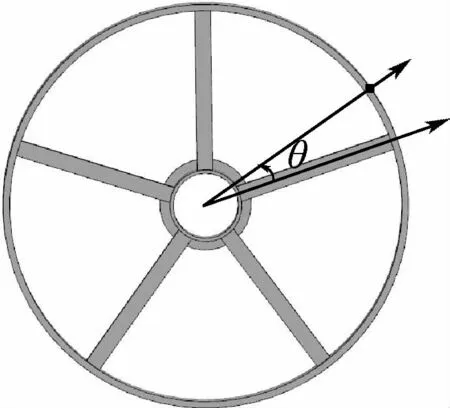
圖6 輪緣徑向剛度極坐標系示意圖Fig.6 Schematic diagram of rim radial stiffness in polar coordinate system

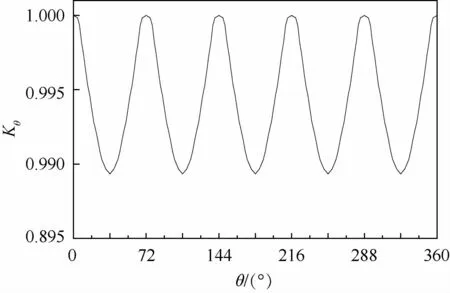
圖7 輪緣無量綱徑向剛度Kθ分布Fig.7 Dimensionless radial stiffness Kθof rim distribution

圖8 輪體旋轉狀態變形放大示意圖Fig.8 Schematic diagram of amplified deformation of wheel body under rotation

1.1.3 輪緣行波振動的影響

輪緣的結構形式為殼體，在旋轉狀態下存在局部振動，其振動示意圖如圖9所示，主要呈現出“花瓣形”的徑向變形。轉動輪盤局部振動的位移主要為軸向，即與轉動軸矢量方向一致，基本只有離心力的作用。而轉動殼體微元素變形如圖10所示，主要為徑向變形u，由于變形速度矢量與轉動速度矢量w存在夾角，二者會形成科里奧利力。也就是說，輪緣在旋轉狀態不僅受離心力的作用使得剛度增加，同時在科里奧利力的作用下對于徑向位移為正和負的微元體分別產生剛度增加或減小的影響，進而影響轉動慣量。而這種非確定的微小變化頻率與前后行波的頻率ω相同，即 ΔJ2x（ω）。

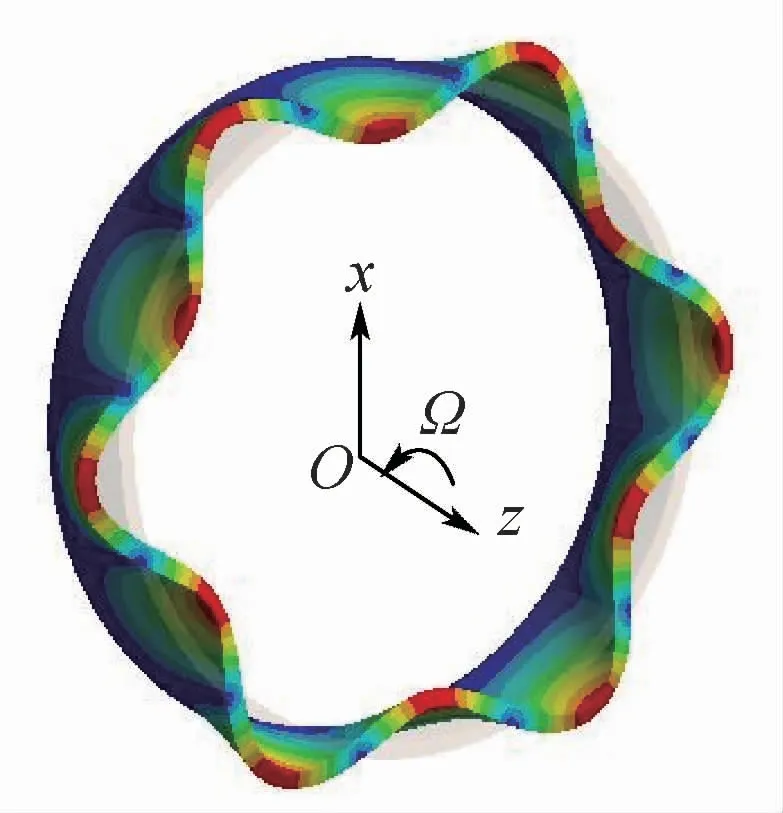
圖9 輪緣振動示意圖Fig.9 Schematic diagram of vibration of rim

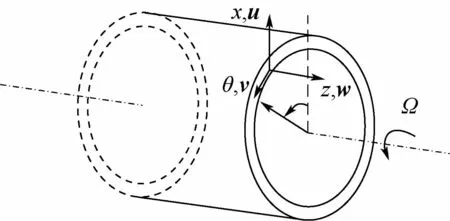
圖10 轉動殼體微元素變形Fig.10 Microelement deformation of rotating shell

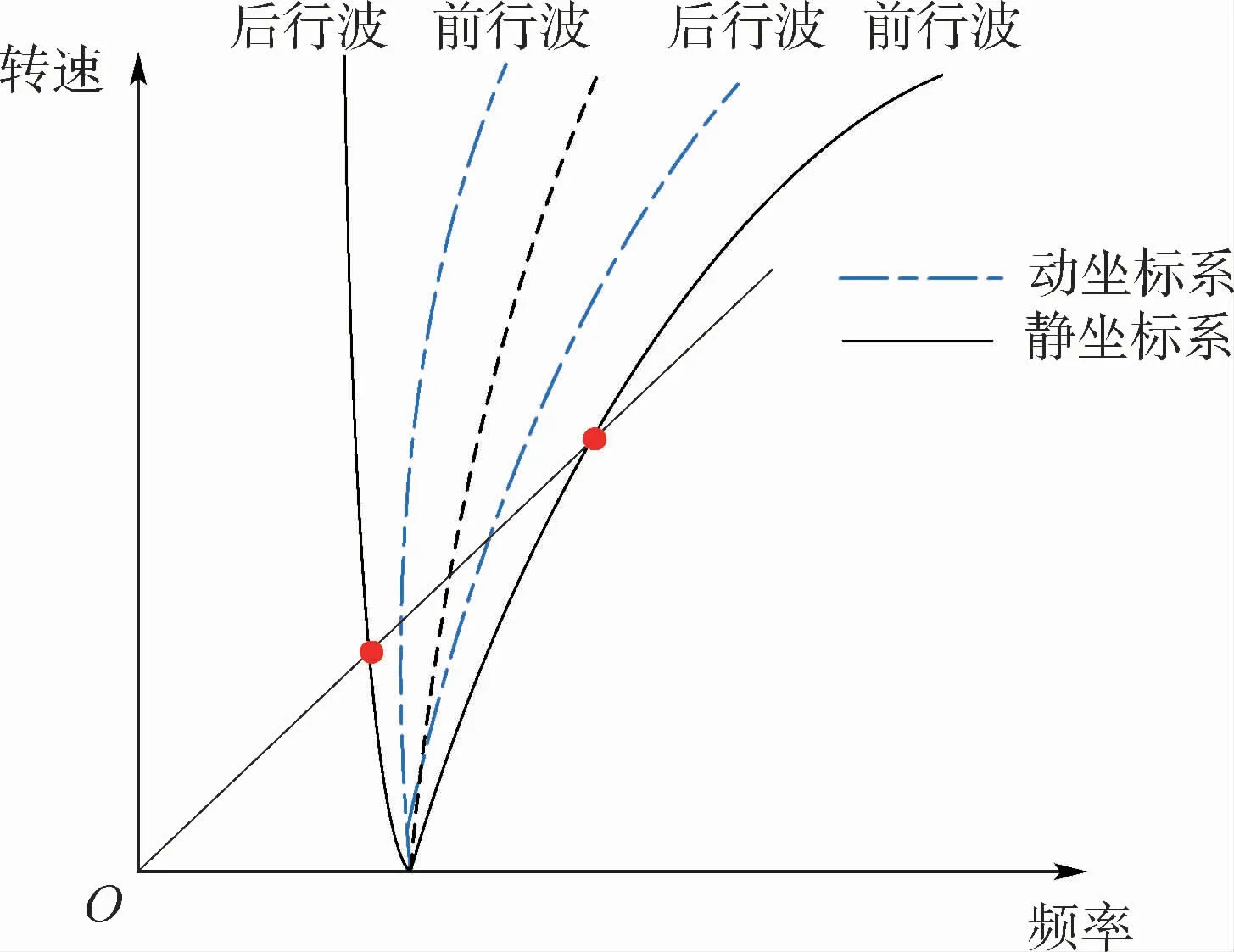
圖11 輪緣共振示意圖Fig.11 Schematic diagram of resonance of rim

輪緣共振示意圖如圖11所示。在科里奧利力的影響下，輪緣的前后行波頻率在與轉動輪體固連的動坐標系中不同，在靜坐標系中的頻率為

式中：ωd為輪緣轉動的固有頻率。

只有當周向波數m=1時，前后行波頻率相同；當m＞1時，前后行波頻率不同[9]，表現在共振圖上的“V”型線。當激振力頻率與正或反進動頻率相等時都會產生較大響應[10]。

綜上，考慮到輪體結構本身的幾何（質量）非均勻性，轉動慣量在旋轉狀態下是與角度有關的確定性函數，但由于剛度分布非均勻引起的離心載荷下微變形及輪緣的局部微振動都會使得直徑轉動慣量具有非確定性，其表達式為

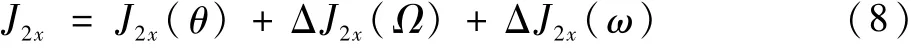
式中：J2x和J2y等價，等式右邊J2x（θ）表示與角度的關系，ΔJ2x（Ω）表示與轉速相關的擾動，ΔJ2x（ω）表示與行波振動頻率相關的擾動。

因此，直徑轉動慣量旋轉狀態下會在一區間內擾動，如圖12所示，仍以角度為自變量，轉動慣量在每一點都具有帶寬，成為系統的參數激勵。

1.2 動量輪結構系統的載荷激勵

動量輪高速旋轉時會將殘余不平衡量放大，引起與轉速成平方關系的振動響應，這種不平衡激勵是最基本的也是不可避免的，然而在平衡精度已經很高的基礎上，結構系統依然存在相對較大的振動，一方面是因為轉子的彈性變形引起的慣性力矩，通過支點將轉子振動的能量轉化為動載荷；另一方面軸承傳播振動能量過程中，本身作為激勵源又會引起復雜的高倍頻激勵載荷。

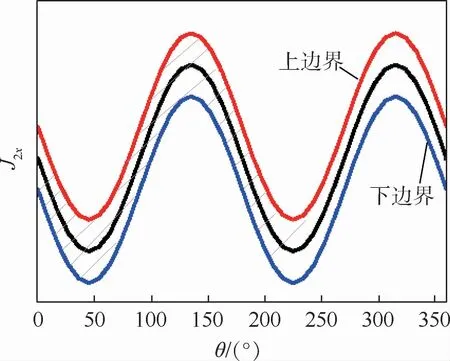
圖12 J2x區間擾動示意圖Fig.12 Schematic diagram of interval disturbance of J2x

1.2.1 支點動載荷

動量輪結構系統旋轉狀態的變形包括離心載荷產生的靜變形及振動變形。靜變形是多種固有模態振型的疊加。整體模態振型主要有3種形式，如圖13所示，分別是徑向平移、徑向搖擺及軸向平移[11]。與Jeffcott轉子不同，單端懸臂支承的動量輪結構系統中，輪體兩側軸承的剛度不完全相同，內部支桿更容易在輪體旋轉作用下發生彎曲變形。

當輪體發生徑向搖擺、高頻彎曲振動變形或者由于結構特征非均勻引起徑向變形不對稱時，都會使得輪體公轉軸和自轉軸產生夾角，從而產生慣性力矩MG。也就是說，作用在支點上的總力矩Mg=不平衡力矩Mz+慣性力矩MG。支點動載荷示意圖如圖14所示。

Mz是由于輪體偏擺產生的不平衡量引起的力矩，其表達式為

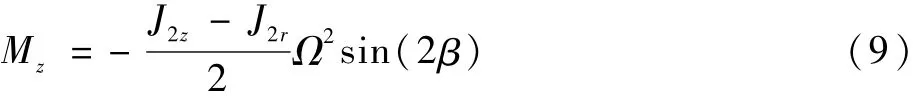
式中：β為軸心線偏離的程度；J2z為輪體的極轉動慣量；J2r為輪體的平均直徑轉動慣量。

慣性力矩MG的表達式為

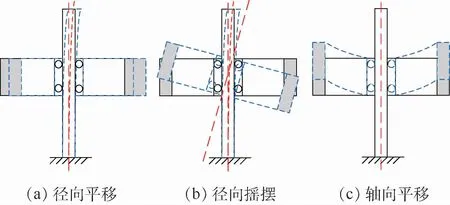
圖13 動量輪整體模態振型示意圖Fig.13 Schematic diagram of modal shape of overall momentum wheel

圖14 支點動載荷示意圖Fig.14 Schematic diagram of dynamic load on fulcrum

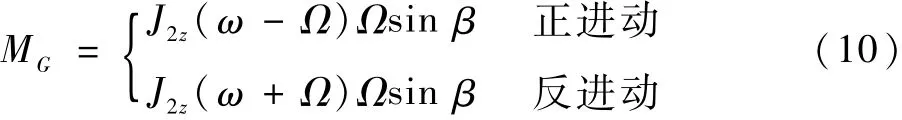
由此可得，當 β很小時，支點所受總力矩大小為

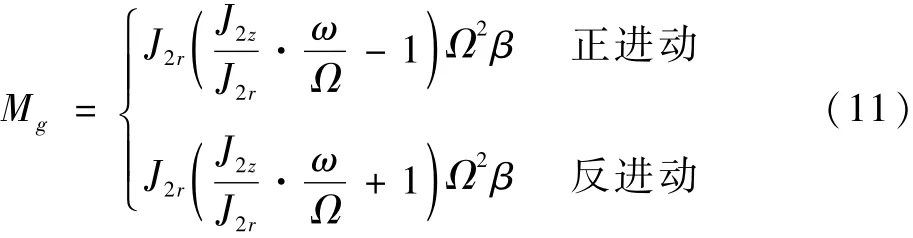
而支點動載荷需滿足如下關系式：

式中：L為支點間距；Fr1為1#軸承外環上作用的徑向載荷；Fr2為2#軸承外環上作用的徑向載荷。

由式（12）可見，支點動載荷與轉速成函數關系，協調進動時支點總力矩的大小與轉速的平方成正比，此時支點動載荷也與轉速平方成正比。實際上，不僅是輪體彎曲時會產生支點動載荷，即使輪體和支桿的變形程度都很小，只要支桿有彎曲（或彎曲的趨勢）時（見圖13（a）、（b）），都會存在支點動載荷，其大小與轉速和彎曲變形的程度有關[12]。

1.2.2 軸承滾子碾壓激勵

支點動載荷會通過軸承組件將輪體的振動能量傳遞給支桿結構和殼體安裝座結構，進而傳遞到衛星上。若支點動載荷很小，經過軸承有可能會衰減，但若支點動載荷很大，就會在支桿上產生較大的振動響應。軸承組件包括球形滾子、內外環及保持架等，由于非連續的結構特征會成為新的振源，產生高倍頻激勵。這種激勵的頻率成分非常豐富，且分布范圍很寬。

高頻激勵產生的主要原因是軸承內部滾子上載荷的分布具有周期性變化規律，會形成與受力滾子數有關的高倍頻激勵。此外，滾動面上的微小幾何誤差會產生與軸承各部件固有頻率相關的高倍頻激勵[13]。

軸承結構示意圖如圖15所示。其各項結構參數決定了零件之間相對的旋轉關系，進一步確定了軸承的特征頻率。設動量輪的轉速為Ω，則軸承外環轉速為 Ω，內環轉速為0。據此可以分別計算出保持架的轉速及滾動體自轉轉速[14]。

根據保持架的線速度為內外滾道線速度的平均值，可得保持架轉速為

根據滾動體與外環接觸點線速度相同，可得滾動體自轉轉速為

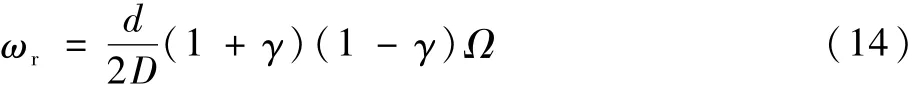
設滾子數為p，軸承轉動頻率為f=Ω/（2π），則軸承的特征頻率如表1所示。

軸承在滾動碾壓過程中會存在上述各種特征頻率成分的激勵及諧波疊加形成的頻率，這是軸承固有的特點，下面分析載荷作用引起的行波激勵。

假設滾動體與滾道為點接觸，按照Hertz接觸彈性理論，可知滾動體與滾道接觸點的法向載荷-位移關系式為

式中：Q為滾動體與滾道接觸點的法向載荷；δ為滾動體與滾道接觸點的位移；k為與兩接觸體材料參數和接觸點曲率半徑都有關的系數[15]。

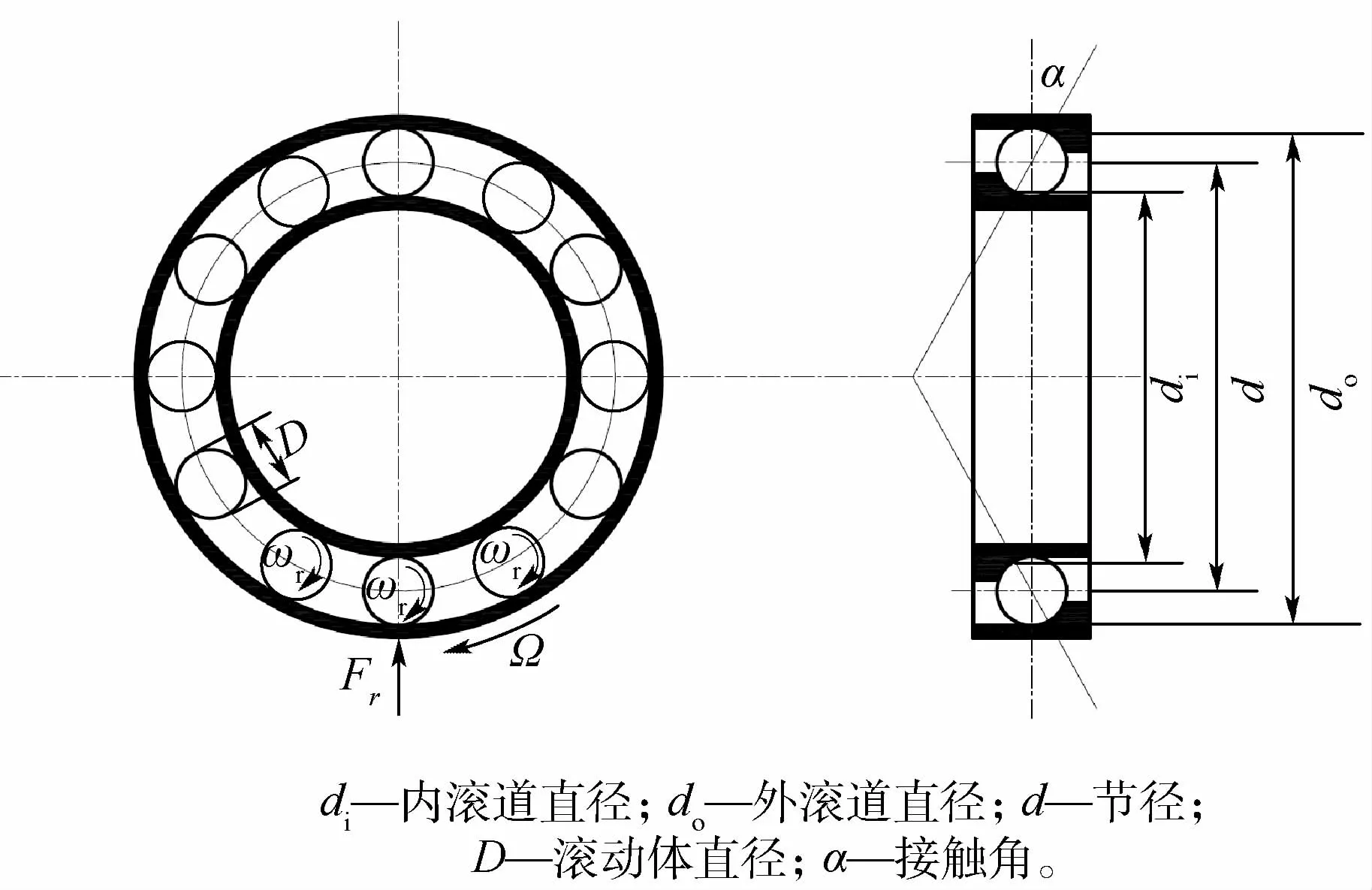
圖15 軸承結構示意圖Fig.15 Schematic diagram of bearing structure

表1 軸承特征頻率Table 1 Bearing characteristic frequency

輪體的振動作用在軸承外環上，表現為徑向（法向）載荷和軸向載荷的形式，再經滾動體傳遞到內環。對于幾何形狀理想的軸承，其軸向載荷可以認為由全部滾動體共同承擔，而徑向載荷由扇區內滾動體承擔。

圖16為徑向載荷作用下的滾動體變形。滾動體與軸心連線相對載荷作用線的夾角為φ時的徑向位移為

式中：δr為φ=0時對應的滾道徑向移動量，此時有 δφ=0=δmax。

式（16）可化為如下比例形式：

結合式（15）和式（17），得

式中：Qφ為夾角為φ時滾動體與滾道接觸點法向載荷；Qmax為最大接觸載荷。

利用力的平衡，受力扇區內滾子上全部載荷在豎直方向的分量應等于軸承外環上作用的徑向載荷，即

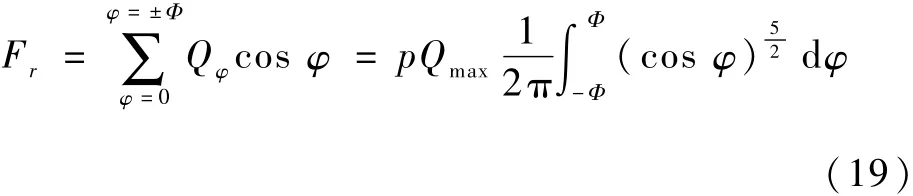
式中：Φ為最大受力扇區半角。

當徑向載荷Fr確定時，可以求出δr，進而可以解得Qφ的分布。受載區的每顆滾動體都受由小變大再變小的周期性載荷。動量輪振動時會產生頻率等于轉頻的多個相位和幅值都不同的徑向載荷以正弦波形式作用于軸承外環。因此，滾動體同一時刻會承受來自多個同頻但不同相位和幅值的波形，疊加后作用于軸承內環，波形經調制后會產生倍頻或次倍頻。取某2個不同的Fri，如圖17所示，都可得到內環某點對應的動載荷。換言之，滾動體的碾壓對軸承內環形成了不同頻率的行波激勵。

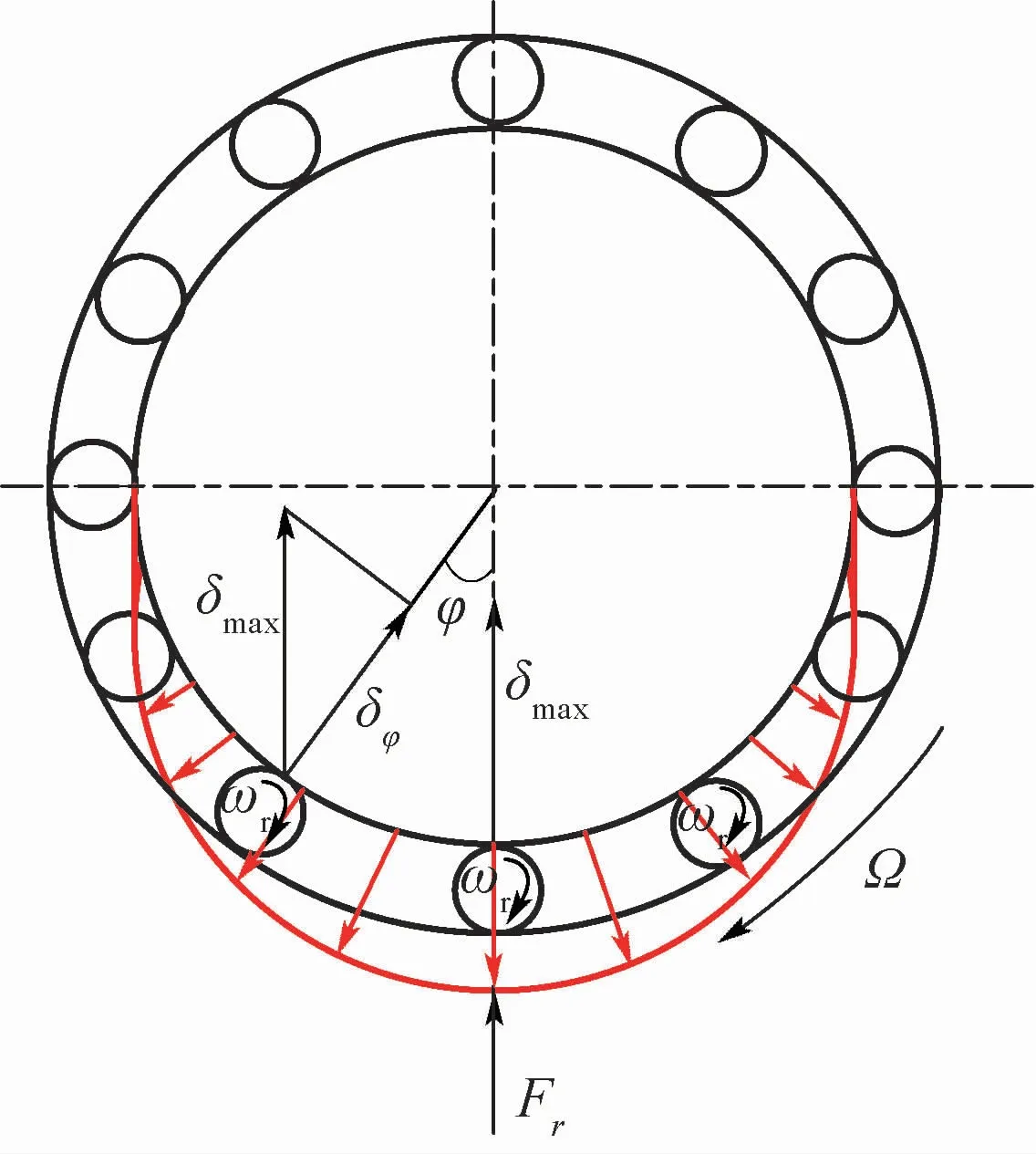
圖16 徑向載荷作用下滾動體變形Fig.16 Deformation of rolling body under radial load

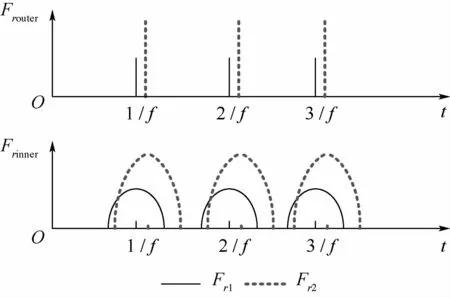
圖17 外環與內環載荷傳遞關系示意圖Fig.17 Schematic diagram of load transfer relationship between outer ring and inner ring

此外，軸承中微小幾何誤差的旋轉效應會使得滾動體與滾道的接觸關系發生改變，從而引起與各零件特征頻率相關的高頻激勵。由于滾動體的碾壓是周期性的沖擊，故其不能看作單一簡諧波，而是可以通過傅里葉變換展開成無窮級數，在頻譜圖上相應表現為一簇原點發射線。當軸承的滾動面幾何誤差疊加時，其相位不同，振動譜線會出現加強或減弱；當誤差間存在相對角速度時，還會出現振動波的調制，更為復雜[16]。

因此，軸承滾動碾壓形成的激勵不僅包括轉頻，還有支點動載荷分布引起的行波振動頻率、軸承特征頻率，以及各頻率的多次諧波和相互之間的調制作用，這些都是動量輪結構系統的載荷激勵。

1.3 其他內部擾振因素

1.1節和1.2節將輪體結構看為一個整體，主要分析了動量輪結構系統的參數激勵和載荷激勵，即動力學方程式（1）中的M 和Q，本節分析其他潛在的擾振因素。

實際的輪體結構為帶有連接界面的非連續系統，為了減小輪輻的局部振動，采用阻尼環結構。阻尼環本身是板殼類零件，包含多個銷釘和螺栓緊固件，在阻尼環的不同位置實現軸向、徑向和周向3個方向的定位約束。連接結構在受力狀態下的離散特性使得在高速旋轉時界面接觸狀態發生變化，一方面影響質量矩陣M 的不確定性，另一方面也會產生不平衡量激勵Q。此外，連接結構的裝配緊度及阻尼環的材料參數等會影響阻尼矩陣C。而剛度矩陣K的擾動主要來源于支點軸承剛度的非線性，其影響因素為支點動載荷。

2 計算仿真與試驗驗證

第1節分析了動量輪結構系統的擾振機理，本節主要通過仿真驗證輪緣的行波振動形成的參數激勵，并通過與試驗的結合共同驗證支點動載荷與軸承產生的載荷激勵。

2.1 實體建模

動量輪結構系統仿真計算模型如圖18所示，其采用的實體結構包括輪體、阻尼環和支桿，有限元模型如圖18（a）所示，采用實體單元網格劃分。輪體為一整體不包含連接結構，將連接件的質量附加于阻尼環上，阻尼環與輪輻設置為綁定接觸。邊界條件如圖18（b）所示，將支桿的一端固定約束，在轉子兩側支點處分別設置軸承單元約束，計算動量輪結構系統的Campbell圖。

圖18 動量輪結構系統仿真計算模型Fig.18 Simulation calculation model of momentum wheel structural system

2.2 仿真結果

動量輪結構系統Campbell圖如圖19所示。動量輪第1階模態為動量輪整體徑向搖擺，由于輪緣的行波振動，會出現“V”型線。第2階模態為整體徑向平移模態，此時輪緣行波振動的周向波數為1，故前后行波頻率理論相同，仍存在微小頻率差異的原因是：支桿彎曲變形引起陀螺力矩及阻尼環局部軸向振動在泊松比作用下會有微量級徑向振動，相應產生科里奧利力。第3階模態主要為阻尼環的振動模態及輪體的軸向平移。做出軸承支點動載荷對應的基頻激勵線，會與一階反進動模態產生交點；做出軸承滾動碾壓產生的二倍頻激勵線，會與動量輪的一階進動產生交點，從而激起共振。因此，通過仿真驗證了輪緣的行波振動。

2.3 試驗驗證

為了驗證動量輪結構系統存在2.2節所述激勵，采用Kistler測力臺設備（見圖20），測試某典型懸臂支承動量輪結構系統在全工作轉速下的輸出擾振力，得到振動響應瀑布圖。

動量輪結構系統振動響應瀑布圖如圖21所示。可知，在無外界激勵的條件下，存在從原點出發的多條激勵曲線，其來源均為結構系統內部，虛線1為與轉速同頻的支點動載荷，其振動響應最大，基本為二次曲線；虛線2為軸承碾壓作用形成的二倍頻激勵，與一階正進動交點處響應達到峰值；此外還存在與軸承特征頻率相關的激勵曲線，每條激勵線與各階模態相交都會激起不同程度的共振，與載荷激勵分析相符。試驗證明，動量輪結構系統存在明顯的前后行波，且頻率基本與仿真相符，由于輪體實際含有連接結構會導致頻率的微小差別。仿真與試驗的綜合驗證了微振動機理分析的正確性。

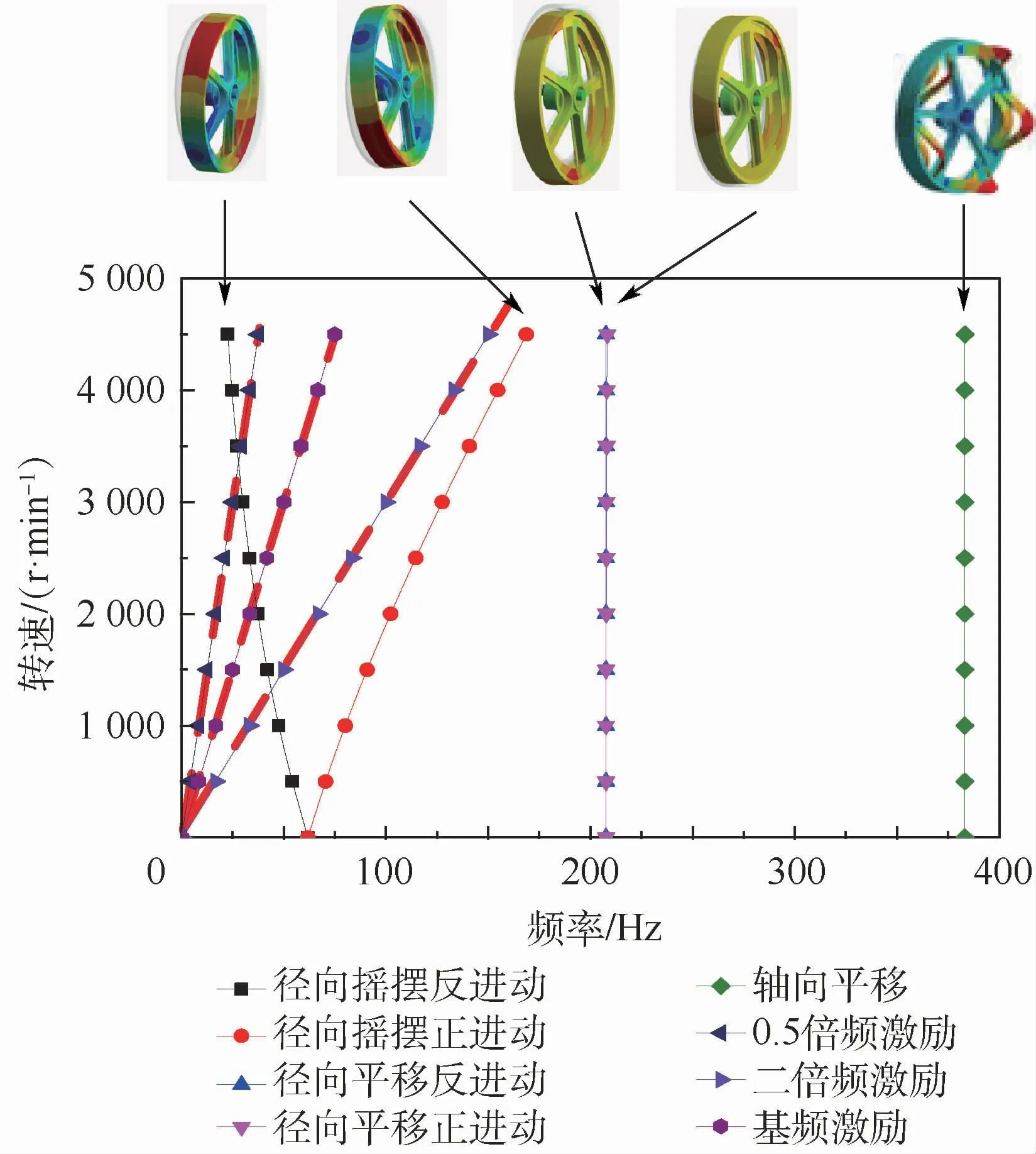
圖19 動量輪結構系統Campbell圖Fig.19 Campbell diagram of momentum wheel structural system

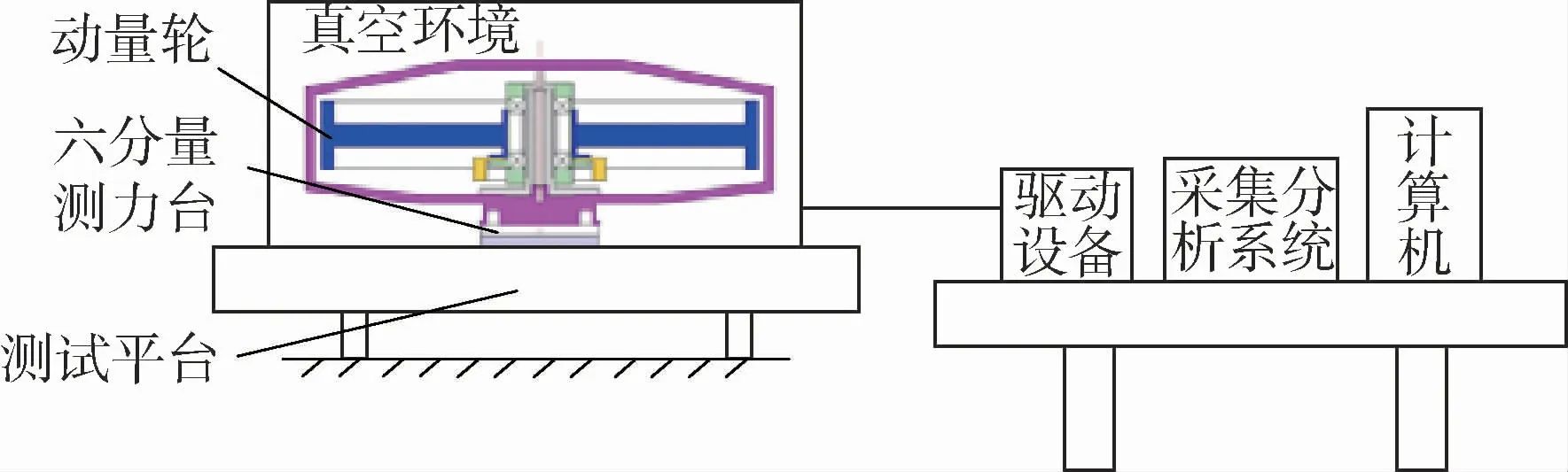
圖20 Kistler測力臺設備Fig.20 Kistler dynamometer equipment

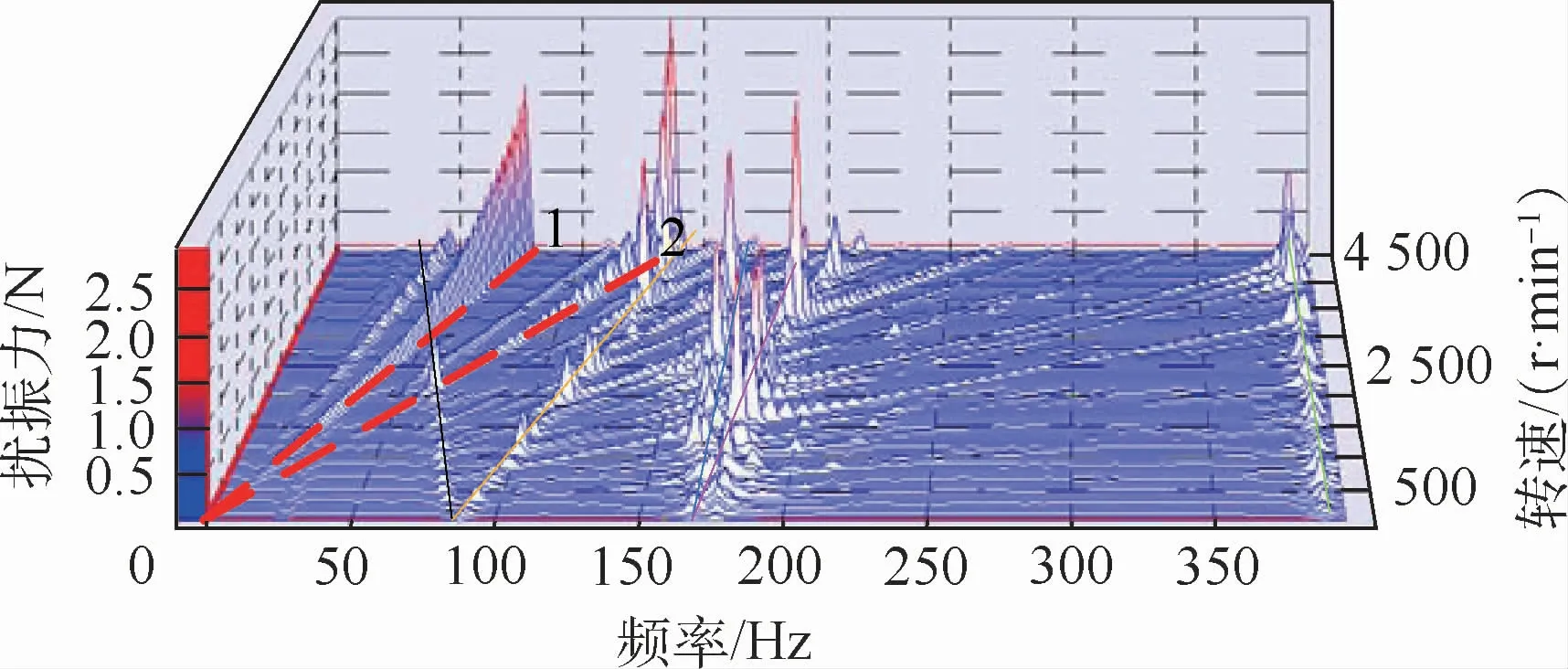
圖21 動量輪結構系統振動響應瀑布圖Fig.21 Waterfall diagram of vibration response of momentum wheel structural system

3 結 論

本文針對單端懸臂支承方式的動量輪結構系統，從動力學方程的角度，研究其可能引起微振動的激勵因素，得到如下結論：

1）輪體結構為輪緣-輪輻的幾何形式，使得其具有質量和剛度分布非均勻的特點，輪體的轉動慣量會在旋轉狀態產生與轉頻相關的微小變化，這種微變形成為結構參數激勵。

2）輪體結構中輪緣部分的局部變形主要為徑向，會產生科里奧利力的作用改變局部剛度，使得轉動慣量產生與行波頻率相關的微小變化，這種微振動成為結構參數激勵。

3）由于動量輪結構系統的支承方式不對稱，更容易發生內部支桿的彎曲，而輪體上的慣性力矩會產生支點動載荷作用在軸承上，與轉頻成二次方關系。而由于軸承結構的不連續，會將支點動載荷發散成高次諧波傳遞到支桿結構上，共同作為結構系統的載荷激勵。

4）實際動量輪結構中還存在其他存在內部激勵源，如連接界面的裝配誤差會影響阻尼等結構參數，軸承剛度的非線性會影響剛度等結構參數。

5）通過仿真驗證了行波振動引起的參數激勵；通過與試驗相結合驗證了支點動載荷及軸承引起的高頻載荷激勵。