GRADUAL HAUSDORFF METRIC AND ITS APPLICATIONS

ZHOU Cai-li,CHEN Xin

(College of Mathematics and Information Science,Hebei University,Baoding 071002,China)

Abstract:This paper is devoted to study of gradual Hausdorff metric introduced by Zhou and Zhang and its application.By means of relationships between gradual numbers and fuzzy numbers,we prove thatis a gradual metric space.And then,we apply gradual Hausdorff metric to fuzzy random variables and obtain new strong law of large numbers for fuzzy random variables,which enrich and deepen the theory of fuzzy numbers and fuzzy random variables.

Keywords: gradual number;gradual Hausdorff metric;fuzzy random variable;strong law of large numbers

1 Introduction

How to define fuzzy metric is one of the fundamental problems in fuzzy mathematics.There are two approaches in this field till now.One is using fuzzy numbers to define metric on ordinary spaces,first proposed by Kaleva[1],following which fuzzy normed spaces,fuzzy topology induced by fuzzy metric spaces,fixed point theorem and other properties of fuzzy metric spaces are studied by a few researchers(see e.g.,[2–5]). The other is using real numbers to measure the distances between fuzzy sets.The references of this approach can be referred to[6–8],etc.

In above literature,the most often proposed fuzzy sets are fuzzy numbers[9]. But it is well known that fuzzy numbers generalize intervals,not numbers and model incomplete knowledge,not the fuzziness per se.Furthermore,fuzzy arithmetic inherit algebraic properties of interval arithmetic,not of numbers.There were some authors who tried to equip fuzzy numbers with a group structure.This kind of attempt suggests a confusion between uncertainty and gradualness.Hence the name“fuzzy number”used by many authors is debatable.Recently,the authors[9]introduced a new concept in fuzzy set theory as“gradual numbers”.Gradual numbers express fuzziness only,without imprecision,which are unique generalization of real numbers and equipped with the same algebraic structures as real numbers(addition is a group,etc.).In the brief time since their introduction,gradual numbers were researched by many authors(see e.g.,[9–13]). In particular,a fuzzy number can be denoted as a crisp interval of gradual numbers which can be bounded by two special gradual numbers.By virtue of considering such a structural characterization of fuzzy numbers,Zhou and Zhang[14]generalized classical Hausdorff metric to the space of fuzzy numbers and introduced the gradual Hausdorff metric. This paper is a continuity of[14]. In this paper,we investigate further properties for gradual Hausdorff metric and apply this metric to fuzzy random variables.

The organization of the paper is as follows. In Section 2,we state some basic results about gradual numbers,fuzzy numbers,fuzzy random variables,gradual Hausdorff metric,etc.In Section 3,we first investigate further properties for gradual Hausdorff metrics.And then,we apply gradual Hausdorff metric to fuzzy random variables and obtain a new strong law of large numbers for fuzzy random variables.

2 Preliminaries

In this section,we state some basic concepts about gradual numbers,fuzzy numbers,gradual Hausdorff metric,fuzzy random variables.

Definition 2.1[9]A gradual numberis defined by an assignment functionfrom(0,1]to the real numbers R.Naturally a nonnegative gradual number is defined by its assignment function from(0,1]to[0,+∞).

In the sequel,the set of all gradual numbers(resp. nonnegative gradual numbers)is denoted by R(I)(resp.R?(I)).It is clear that any real number b ∈R can be viewed as an constant assignment functionfor each α ∈(0,1].We call such elements in R(I)constant gradual numbers.

Definition 2.2[9]Suppose that ?is any operation in real numbers andandare two any gradual numbers with assignment functionsandrespectively.Thenis the gradual number with an assignment functiondefined by

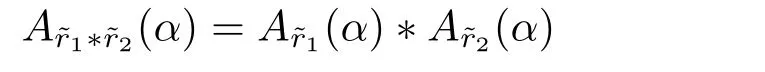
for each α ∈(0,1],where ?∈{+,?,×,÷}.

Definition 2.3[14]Let∈R(I).

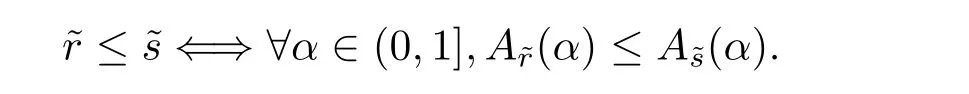
(2)The maximum and minimum operations ofandare defined as follows:for all α ∈(0,1]，

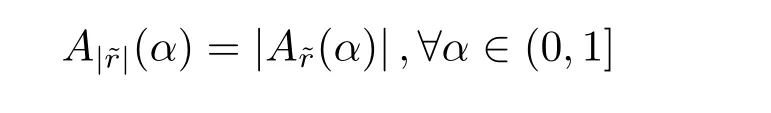
is called the absolute value of

In the following,we describe some basic results for fuzzy numbers.A fuzzy number is a normal,convex,upper semicontinuous and compactly supported fuzzy set on R. In the sequel,letdenote the family of all fuzzy numbers.According to Fortin,Dubois and Fargier[9],a fuzzy numbercan be viewed as a particular gradual intervalwhereandare defined by

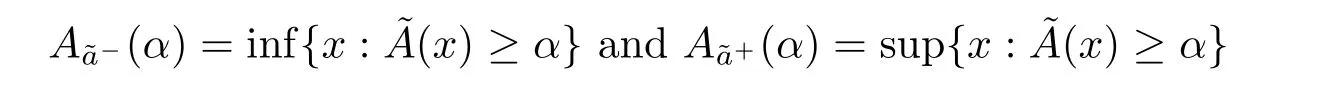
for each α ∈(0,1],respectively.A gradual numberas a degenerate fuzzy number

In the same way as defining crisp interval,we can define equality,sum and scalar multiplication on the space of fuzzy numbers as follows:letandbe inand.Define

Definition 2.4[14]Letandbe in.Define

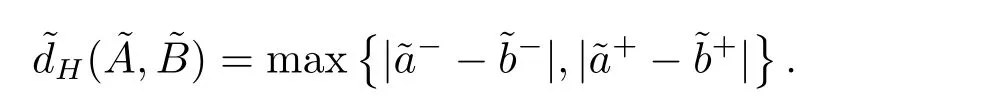
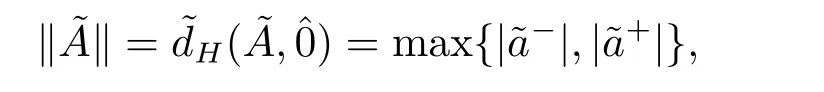
Definition 2.5[14] LetandWe call thatconverges towith respect to the gradual Hausdorff metricif and only if

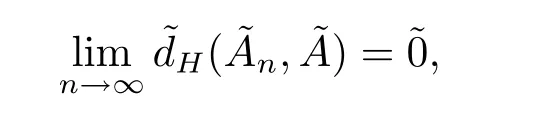
Theorem 2.6[14]Letconverges to fuzzy numberwith respect toif and only ifconverges toandconverges tosimultaneously.

Definition 2.7[15]A gradual metric space is an ordered pair,where X is any set andis a mapping satisfying

Definition 2.8[16] A mappingis said to be gradual random variable associated with a measurable spaceif for each α ∈(0,1],the real-valued mappingdefined by?ω ∈?,is a classical random variable associated with

Definition 2.9[17]Given a probability spacea mappingis said to be a fuzzy random variable(or FRV for short)if for all α ∈(0,1]the two real-valued mappings

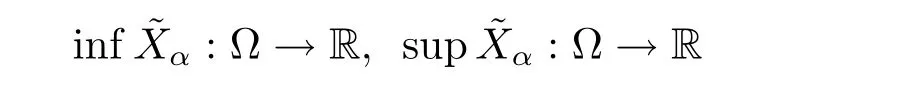
(defined so that for all ω ∈? we have thatare realvalued random variables.

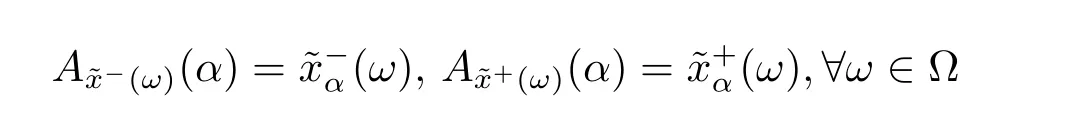
are two gradual random variables.In the following,we denoteby

For more details on gradual numbers,fuzzy numbers,gradual Hausdorff metrics,gradual random variables,fuzzy random variables,we refer the reader to[9,10,12–16].

3 Main Results

Theorem 3.1is a gradual metric space.

ProofLetandbe inFirst,we show thatif and only ifIfthen

In the following,we show that for anyAccording to Definition 2.2 and Definition 2.3,we haveandIt follows that

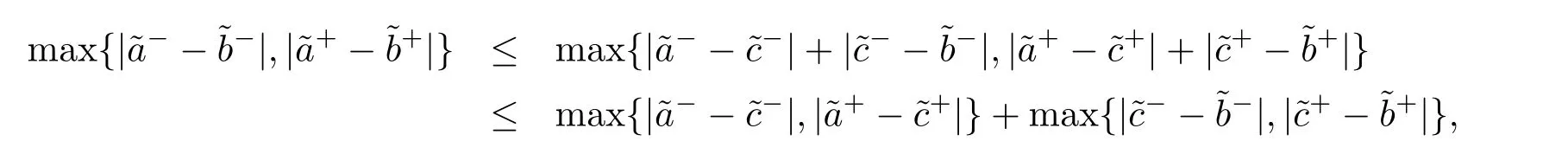
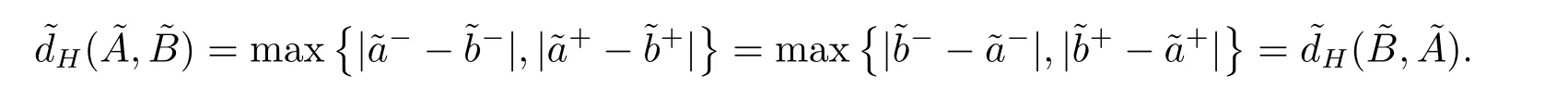
This completes the proof.

Theorem 3.2Letandbe two fuzzy random variables.Thendefined by

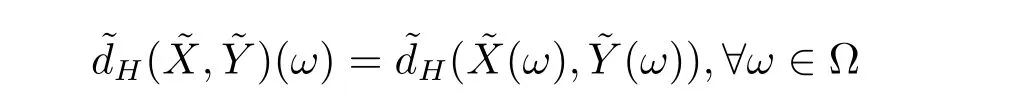
is a gradual random variable.Especially,is a gradual random variable.

ProofSinceandare fuzzy random variables,andare gradual random variables.It follows from Theorem 3.7[16]thatandare gradual random variables. Thenis a gradual random variable. Especially,ifis a gradual random variable.

Definition 3.3A fuzzy random variableis called integrable ifandare integrable simultaneously.In this case,we call the expectationofexists ifand.

From Definition 3.3,we can show thatexists.

Theorem 3.4Letandbe two fuzzy random variables.

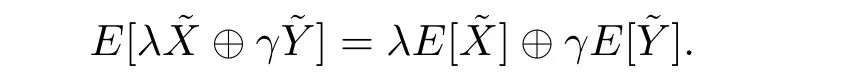
Proof(1) LetIf for anythenand,i.e.,andare constant valued gradual random variables.It follows from Theorem 3.10[16]thatandThus,we have

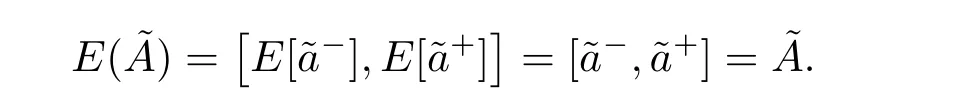
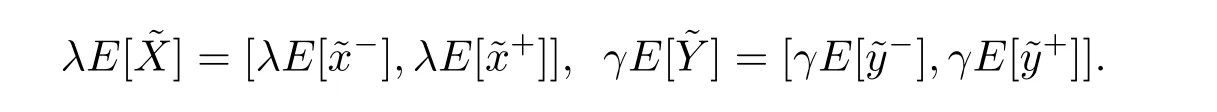
It follows that

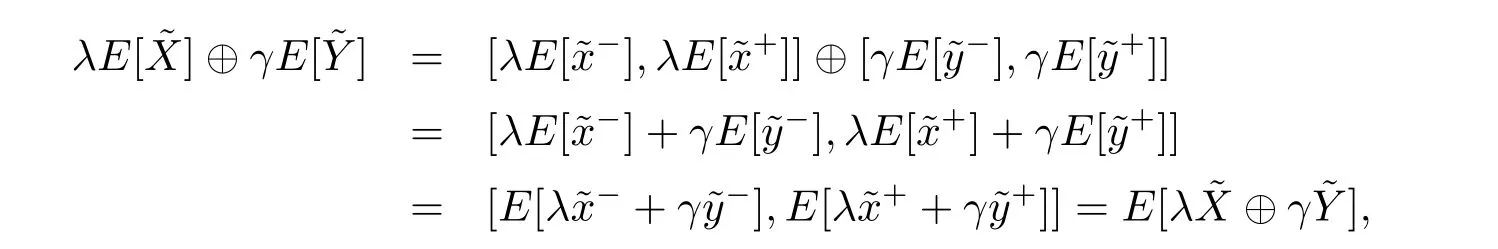
Definition 3.5Letbe a sequence of fuzzy random variables.Ifandare sequences of independent and identically distributed gradual random variables,thenis called a sequence of independent and identically distributed fuzzy random variables.

Theorem 3.6Letbe a sequence of independent and identically distributed fuzzy random variables on the same probability spaceand,n=1,2,···have the same expected value.Then we have

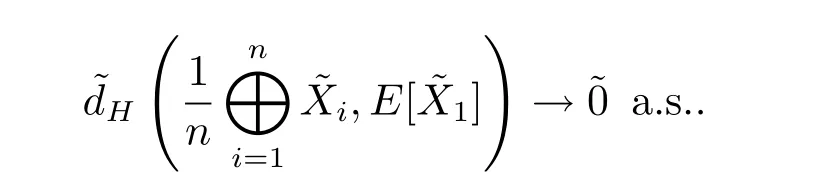
ProofTo end the proof,we use Theorem 2.6.We have andSinceis a sequence of independent and identically distributed fuzzy random variables,andare sequences of independent and identically distributed gradual random variables. It follows thatandare sequences of independent and identically distributed classical random variables for each α ∈(0,1].Since(n=1,2,···)have the same expected value,for each n ∈N,which implies thatand.Then we have

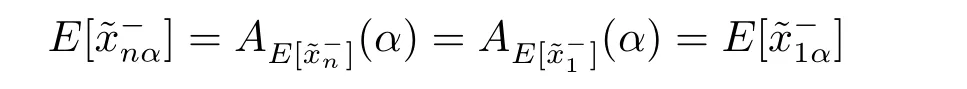
and

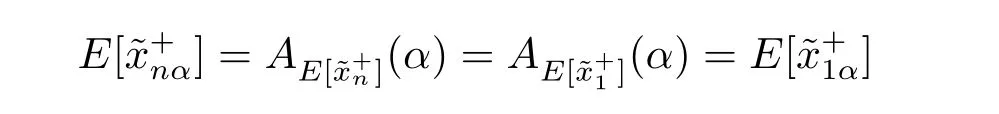
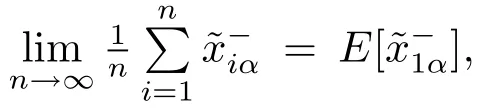
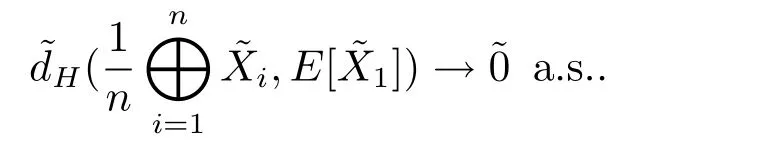
This completes the proof.

Conclusions

In the paper,we firstly investigate further properties for gradual Hausdorff metric introduced by Zhou and Zhang.And then,we apply gradual Hausdorff metric to fuzzy random variables and obtain a new strong law of large numbers for fuzzy random variables.In all applications which involve metric and random variable,when data are fuzzy-valued,the conclusions given in this paper can be applied.