ASYMPTOTIC BEHAVIOR OF COMPRESSIBLE NAVIER-STOKES FLUID IN POROUS MEDIUM
YUAN Guo-zhi,ZHAO Hong-xing
(College of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China)
Abstract:We study the behavior of the solution to the full compressible Navier-Stokes fluid in porous medium. By using standard energy and two-scale convergence,we prove the strong convergence of the density and the temperature with characteristic size of the pores ε in Rn for n=2 or 3 and obtain the homogenized for this model,when ε →0,which gives another explanation to the results in references.
Keywords: asymptotic analysis;homogenization;Navier-Stokes flow;Gibbs’equation
1 Introduction
Homogenization is a mathematical tool that allows changing the scale in problems containing several characteristic scales.Typical examples of its utilization are finding effective models for composite materials,in optimal shape design,etc.Another important example,which we are interested in,is the fluid mechanics of the flow through porous medium.
In porous medium,there are at least two length scales:microscopic scale and macroscopic scale.The partial differential equations describing a physical phenomenon are posed at the microscopic level whereas only macroscopic quantities are of interest for the engineers or the physicists.Therefore,effective or homogenized equations should be derived from the microscopic ones by an asymptotic analysis.To this end,it is convenient to assume that the porous medium has a periodic structure.
A number of known laws from the dynamics of fluids in porous media were derived using homogenization.The most well-known example is Darcy’s law,being the homogenized equation for one-phase flow through a rigid porous medium.Its formal derivation by twoscale expansion goes back to the classical paper by Sanchez-Palencia[1],Keller[2]and the classical book Bensoussan[3]. It was rigorously derived by using oscillating functions by Tartar[4]. In other cases of periodic porous media,we refer the readers to the papers by Allaire[5–8]and Mikelic[9,10].Other works can be seen in[11–13]and the references therein.Besides the Darcy law,Brinkman[14]introduced a new set of equations,which is called the Brinkman law,an intermediate law between the Darcy and Stokes equations.The so-called Brinkman law is obtained from the Stokes equations by adding to the momentum equation a term proportional to the velocity(see[7]).
Inspired by the work from Feireisl[11],we consider the asymptotic behavior of a compressible fluid in a periodic medium.Before stating the system,let us recall the domain we consider.A porous medium is defined as the periodic repetition of an elementary cell of size ε(we assume thatto be an integral)in a bounded domain ? of Rnwith n=2,3.The solid part of the porous medium is also taken of size ε.The domain ?εis then defined as the intersection of ? with the fluid part.We consider the density dependent fluid governed by the full compressible Navier-Stokes equations.So,we have the following equations
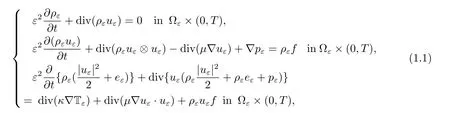
We also assume that uεsatisfies

and in order to fix ideas we impose Neumann boundary conditions on Tεnamely

where n,as usual,the unit outward normal to ??ε.
In this paper,we assume that the initial conditions

are bounded in L∞(?ε).
In this paper,we also assume that the transport coefficientsandsatisfying the following conditions
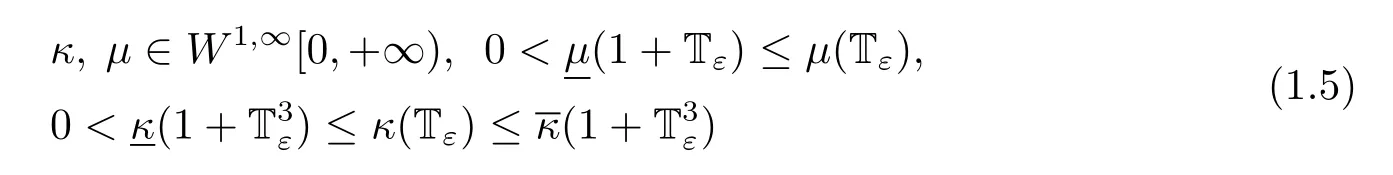
for all Tε≥0.are positive constants.
Let us recall that the equation with temperature in(1.1),it is equivalent(at least formally)to

For simplicity,in this paper,we consider the models in astrophysics and the state equation for the pressure pεand the internal energy eεsatisfying the Joule’s law(see[15])
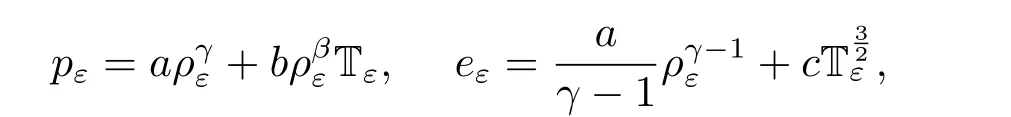
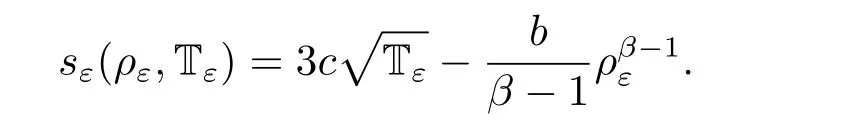
We assume that the initial condition
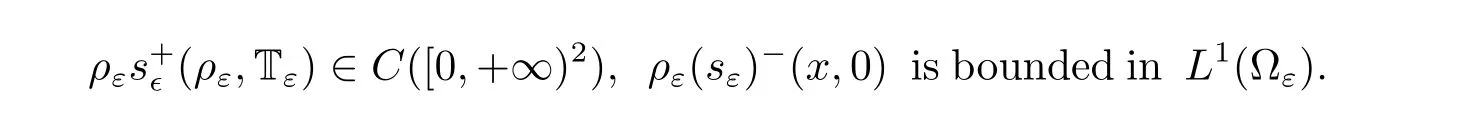
Let us also recall that,at least formally,the following identity holds
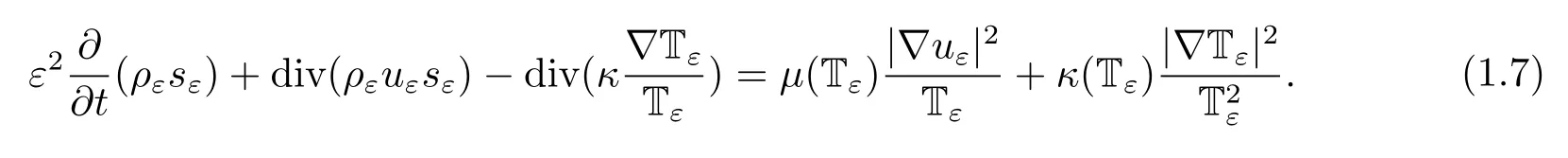
Our aim here is to investigate the asymptotic behaviors of ρε,uεandas ε →0 under the assumptions mentioned above.The main difficulty in this paper is how to pass the limit in the momentum and energy equations.To overcome this obstacle,we have to regularize the system both in time and in space before we can pass the limit.In this paper,we exert the conditions on the entropy to get the estimates.Moreover,we rigorously proved that the low boundary of γ would be n when passing the limit to the convection term.At the limit process,we fall back on the two-scale convergence method to obtain the homogenized model.Those are quite different from[11].
1.1 The Domain
Let ? be an open bounded subset of Rnwith n=2 or 3 and defined Y=[0,1]nto be the unit open cube of Rn. Let Ysbe a closed smooth subset of Y with a strictly positive measure.The fluid part is then defined by Yf=Y ?Ys.Let θ=|Yf|.The constant θ is called the porosity of the porous medium.We assume that 0<θ<1.
Repeating the domain Yfby Y-periodicity,we get the whole fluid domain Df,we can write it as

Then the solid part is defined by Ds=Rn?Df.It is easy to see that Dfis a connected domain,while Dsis formed by separated smooth subsets.In the sequel,we denote for all k ∈Zn,Yk=Y+k and thenFor all ε,we define the domain ?εas the intersection of ? with the fluid domain scaled by ε,namely,?ε=? ∩εDf.To get a smooth connected domain,we will not remove the solid part of the cells which intersect with the boundary of ?.Now,the fluid domain can be also defined by

1.2 Some Notations and Preliminaries
Throughout this paper,we denote Lp(0,T;Lq(X)),the time-space Lebesgue spaces,where X would be ? or ?ε;Ws,p(X)is the classical Sobolev space with all functions,whose all derivatives up to order s belong to Lpandis the subset of W1,p(X)with trace 0 on X.We also denotethe dual space ofwhere p'is the conjugate exponent of p;C is a constant that may differ from one place to another.Throughout this paper,we use||·||Xto denote the modules for all vectors and matrixes if there is no confusion.
Due to the presence of the holes,the domain ?εdepends on ε and hence to study the convergence of{uε,ρε,pε},we have to extend the functions defined in ?εto the whole domain.This can be done in two different possible ways.
Definition 1.1For any fixed ε ∈L1(?ε),we define
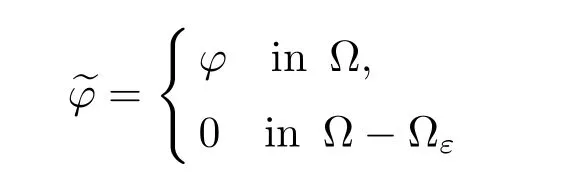
the null extension and
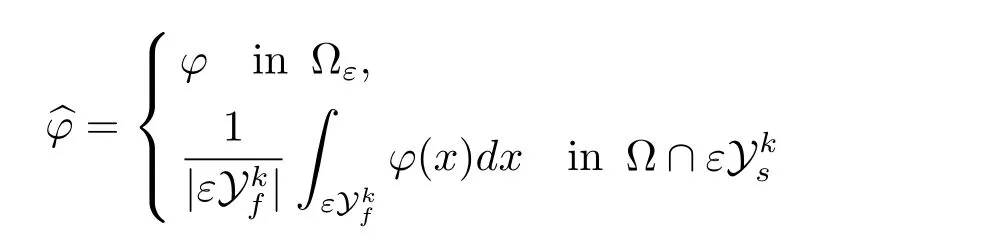
the mean value extension.
The relation between the weak limits of both types of extensions is given by the following lemma(see[13]).
Lemma 1.1For all ωε∈L1(?ε),the following two assertions are equivalent
A very important property of the porous media is a variant of the Poincare’s inequality.Due to the presence of the holes in ?ε,the Poincare’s inequality reads in[12].
Lemma 1.2Let 1 ≤p,q<∞andthen
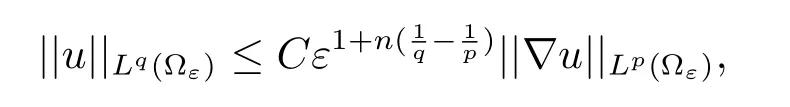
where C depends only on Yfand p,q satisfies(1)1 ≤p
We also need the restriction operator constructed by Tartar(see[4]).
Lemma 1.3There exists an operator Rεwith the following properties
1.Rεis a bounded linear operator onranging inp ≥2;
2.Rε[?]=?|?εprovide ?=0 in ? ??ε;
3.divx?=0 in ? implies divxRε[?]=0 in ?ε;
In addition,we can find the restriction operator Rεsatisfies a compatibility relation with the extension operator introduces in Definition 1.1,namely,
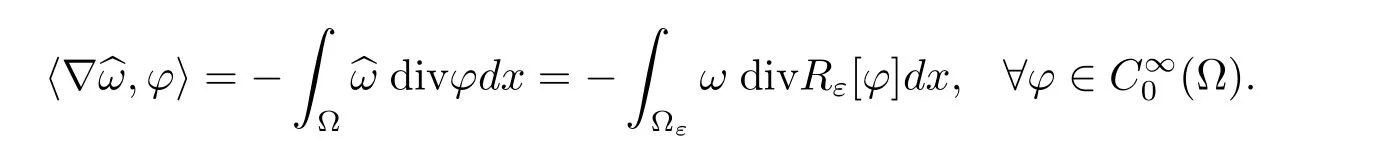
Lemma 1.4(Bogovskii operator)There exists a linear operator Bεwith the properties:if f ∈Lp(?ε),then φ=Bε[f]such that
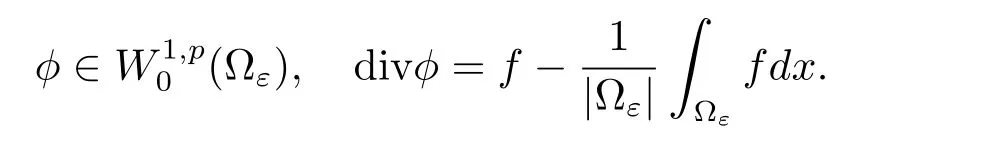
Moreover,the following estimates is satisfied
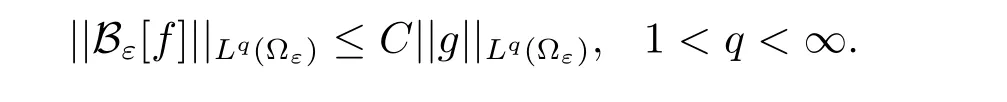
There are many ways to construct Bε.An explicit formula was proposed by Bogovskii[16]on Lipschitz domains.Some properties of Bεwere discussed by Galdi[17].In the domain with porous medium,the relevant estimates were obtained by Masmoudi[13].
Finally,we define the permeability matrix A.For 1 ≤i ≤n,let(ωi,πi)∈H1(Yf)×L2(Yf)/R be the unique solution of the following system
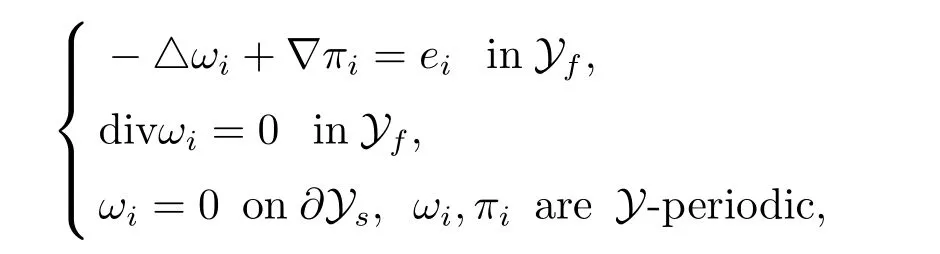
where eiis the standard basis of Rn. SetThen we get the cell problem
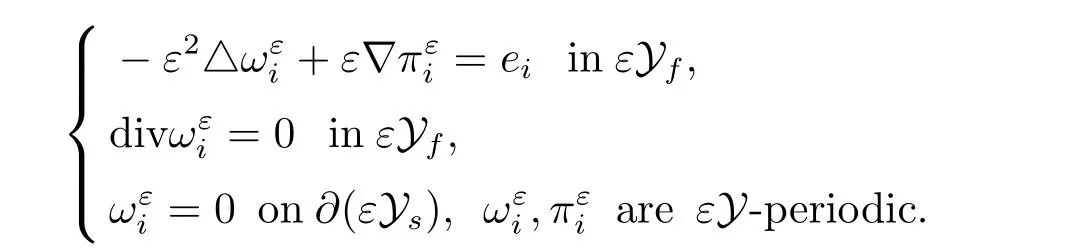
Lemma 1.5Letbe the solution to the cell problem and be extended to zero outside ?ε.Then the following estimates hold
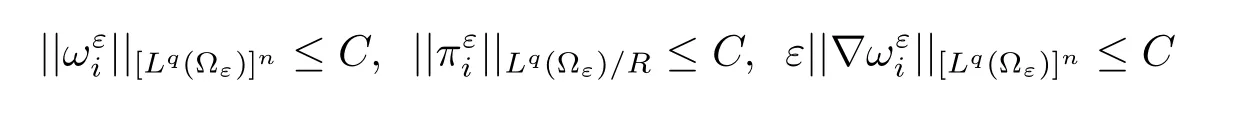
for any 1 ≤q ≤+∞,C only depends on q and Yf.
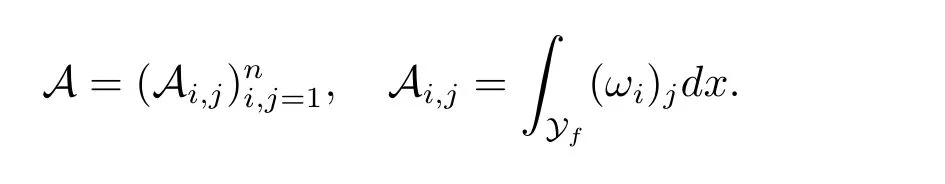
It is easy to see that A is a symmetric positive defined matrix.The form of the permeability matrix has different form if Yshas different forms.For more information about A,we refer the interested readers to Allaire[7]for detail.
1.3 The Main Results
Now we introduce the definition of weak solution to the systems(1.1)–(1.4)
Definition 1.2We shall say that a trio{uε,ρε,pε}is a weak solution of(1.1),supplemented with the boundary and initial conditions(1.2)–(1.4)if only if
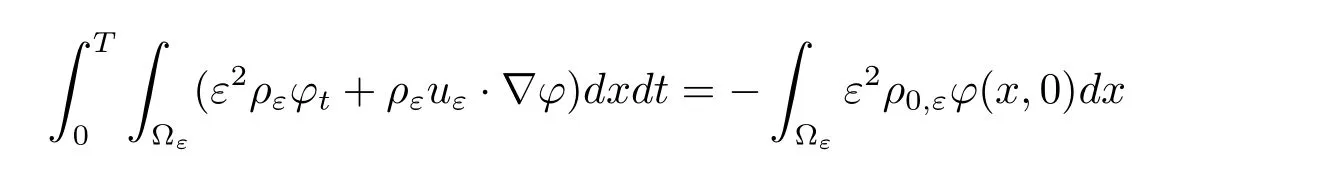
holds for any test function
2.pε∈Lq(?ε×(0,T))for some q>1,and

3.Tε∈L2(0,T;L6(?ε))∩L2(0,T;H1(?ε)),Tε>0 a.a in ?ε×(0,T)and the integral identity

With all the preparation above,we are now in the position to state our main result in this paper.
Theorem 1.1Let{uε,ρε,Tε}ε>0be a family of weak solutions to system(1.1). We assume that γ ≥n for n=2,3 and
Then,there exist three functions u,ρ,such that
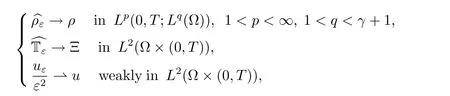

where p,e are given by

and A is the so-called permeability matrix.The specific homogenized entropy s related to the homogenized pressure p and the homogenized inner energy e through Gibbs’equation where s is given by

2 Uniform Bounds
In this section,we collect all available bounds on the family{uε,ρε,Tε}.Let us begin with the basic estimates
2.1 Basic a Priori Estimates
In this subsection,we obtain some estimates for the solutions to system(1.1)which are independent of ε.First,from the conservation of mass,we have ρε∈L∞(0,T;L1(?ε)).We set

Next,integrating(1.7)over ?ε×(0,t)for any t ∈[0,T],we have
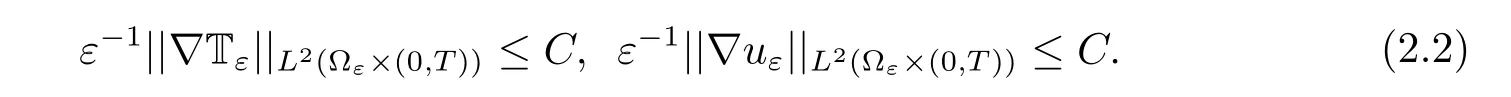
We then deduce the uniform bound of ρε|sε|in L∞(0,T;L1(?ε))and ρεis uniformly bounded inBy Lemma 1.2 and the special sε,eε,we also have
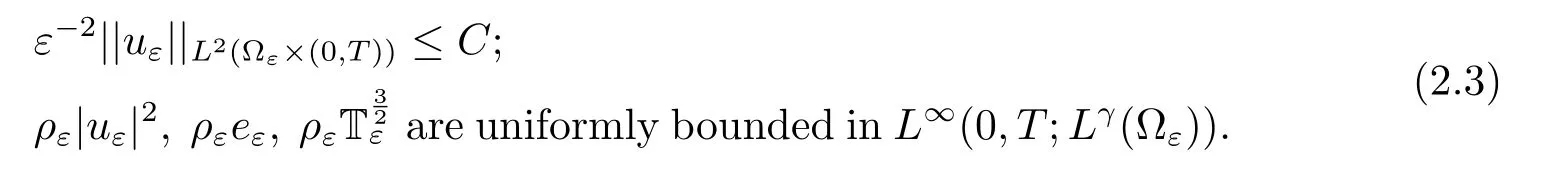
2.2 Refined Temperature Estimatess
In this subsection,we want to deduce the uniform bounds on Tε. Note that we only have the bounds of ?TεandThe estimate on Tεitself isn’t included.To fill this gap,we fall back on the’lemma[18]and the Sobolev embedding theorem in the porous medium
Lemma 2.1Let ? be a bounded Lipschitz domain in R2or R3. Let M,K be two positive real numbers and ρ a non-negative function such that
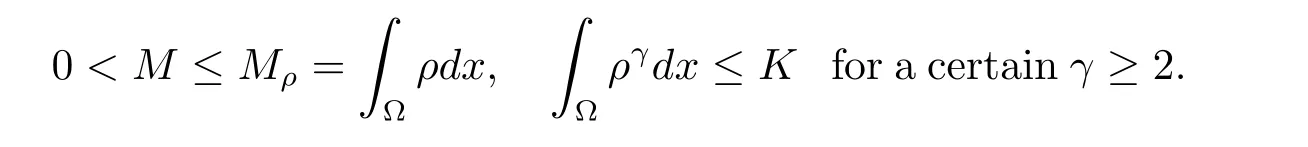
Then there exists a constant C=C(M,K)such that
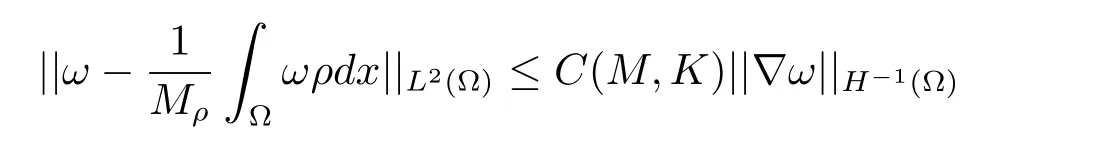
for any ω ∈L2(?).
Proofsee[11].
Following the idea in[11]and[12],we prove the Sobolev embedding theorem in the porous medium has the form.
Lemma 2.2Let v ∈W1,p(?ε).Then we have

ProofObviously,it is enough to show
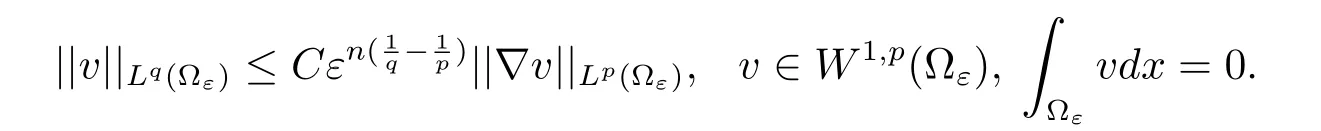
By the definition of the module of Lpand Lemma 1.2,Lemma 1.3,we have
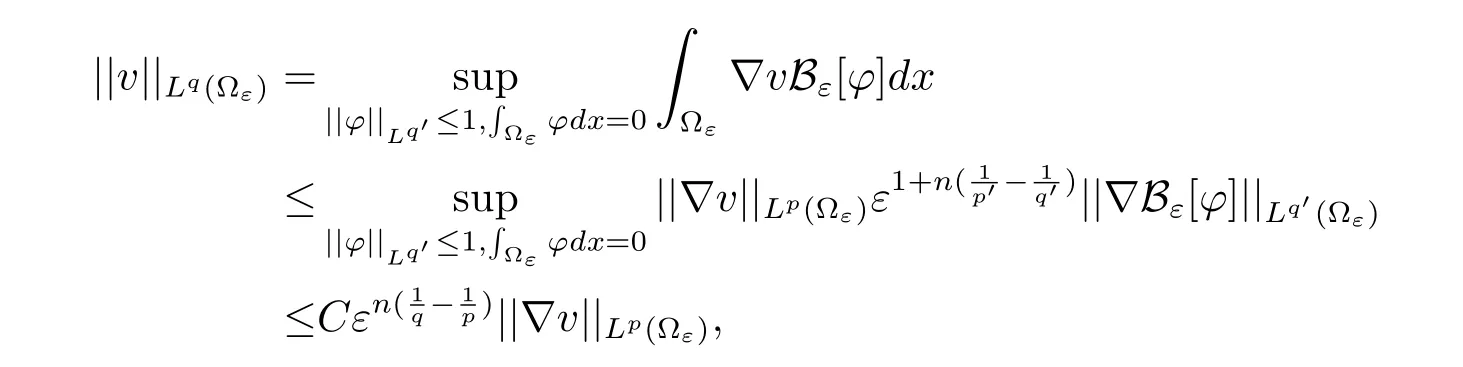
By Lemma 1.3 and(2.2),we obtain
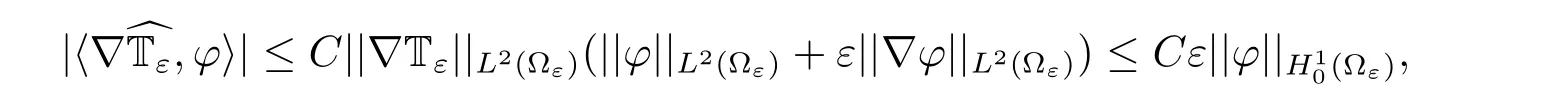
which implies that

Next,we write
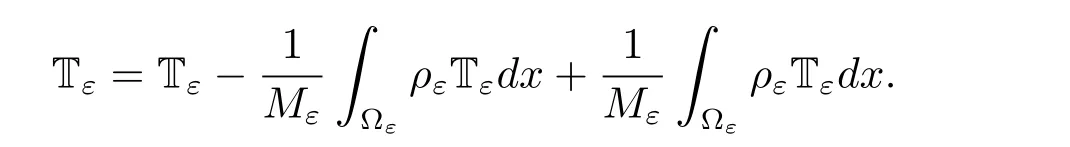
In accordance with Lemma 2.1 and(2.2)–(2.4),we have
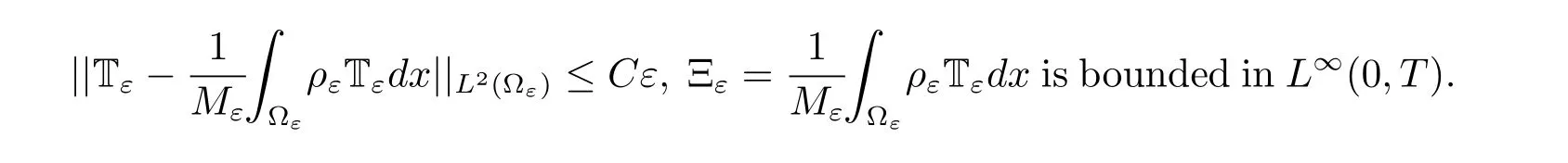

with C independent of ε.
2.3 Refined Density Estimates
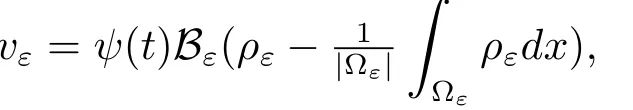
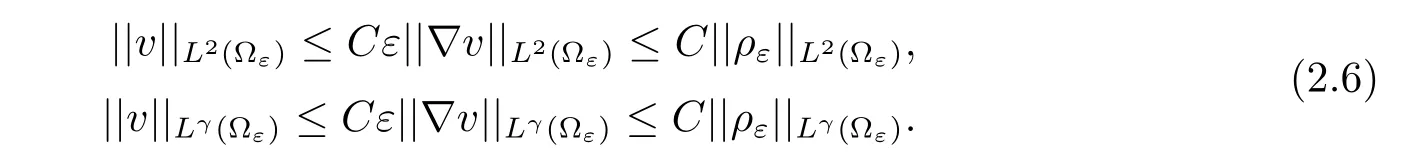
Multiplying the second equation of(1.1)by vε,we get(we drop the dxdt)
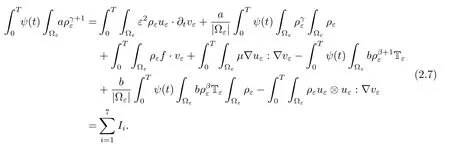
The first term is the most technical and requires some spatial regularization of vε(see[13]).Let us explain how the difficulty related to I1can be solved.The estimation of rest terms are the same as[13].Setsuch that χ(x)≥0,For all δ ∈(0,1),we denoteNext,we denotewhereis defined in Definition 1.1.Then we have the following relation

where rε,δis nothing but a commutator,rε,δ→0 inas δ →0.Now we takein stead of vε. Taking the time derivative of t of vε,δ,we have

It is easy to check that
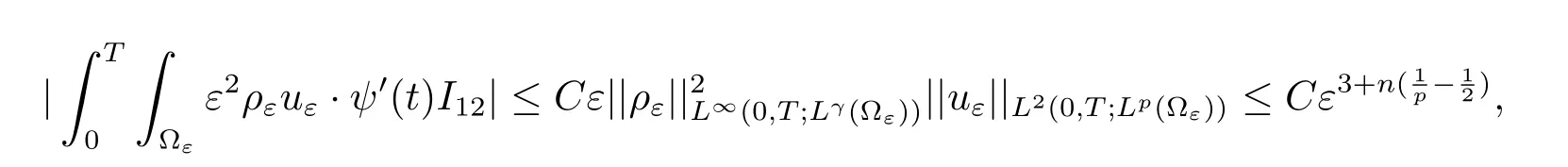
Next,after a straightforward manipulation we have

By Lemma 1.2 and Lemma 1.3,we deduce that
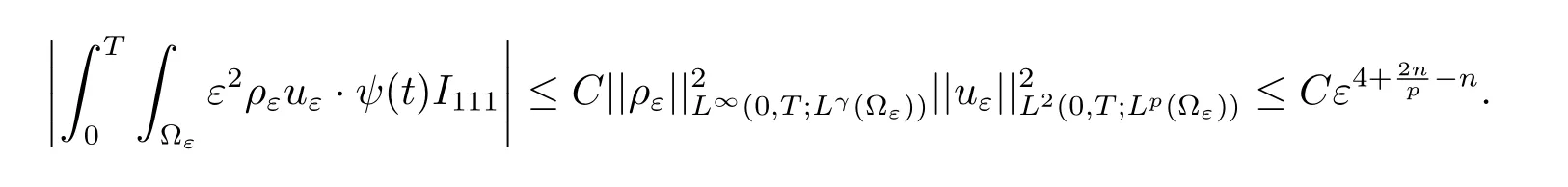
To I112,we have
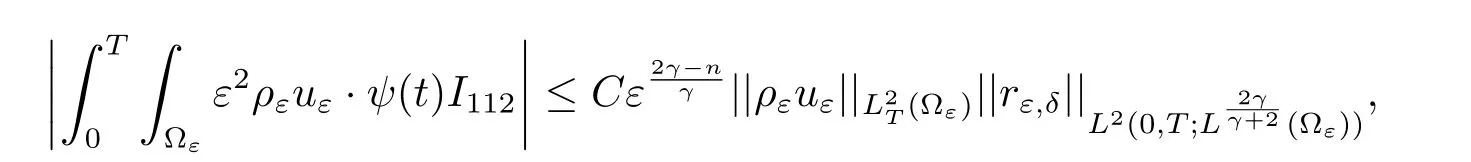
From above,we get the estimate
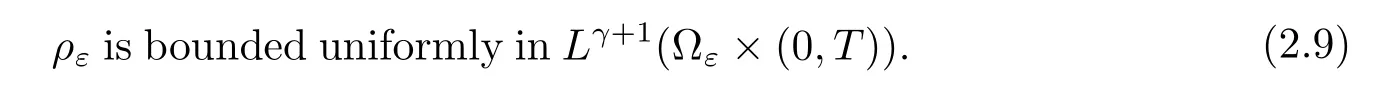
With those estimations,we can also obtainconverges strongly to p in L2(0,T;Ls(?))for some s>1,see[12].
3 Proof of Theorem 1.2
We divide three steps to finish the proof.
Step 1Passing the limit in the continuum equation.As in[13],we can prove that

Multiplying above equation byand integrating over ?×(0,T),we have

Passing the limit and using the strong convergence ofandwe obtain

We then recover the homogenized equation and the initial condition

Step 2Passing the limit in the momentum equations.
To pass the limit,we have to regularize the second equation of(1.1)both x and t.To this end,we setsuch that
Let η1∈(0,1)and setWe also setsuch thatLet η2∈(0,1)and setTakeas the test function,where Tmis the truncated function by integer m andis prolonged by zero outside ?×(0,T),be the solution of the cell problem andWe have
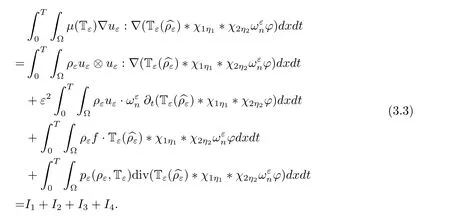
To pass the limit in I1and I2,we can easily deduce that I1→0,I2→0 as ε →0.Now,we can pass the limit in I3and I4sinceconverges strongly,
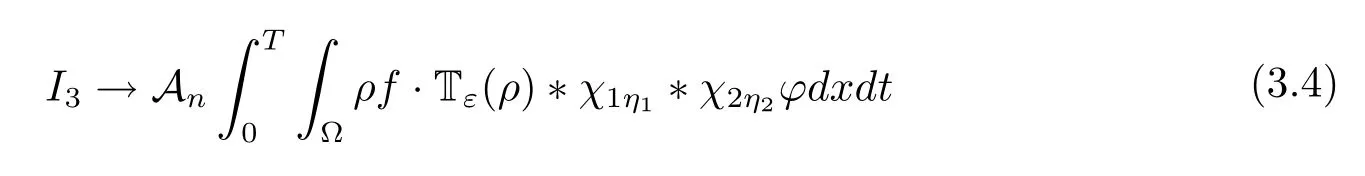
and
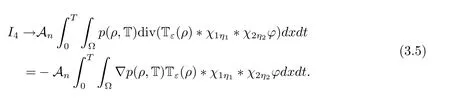
Finally,we consider the limit on the left-hand side.We write it as
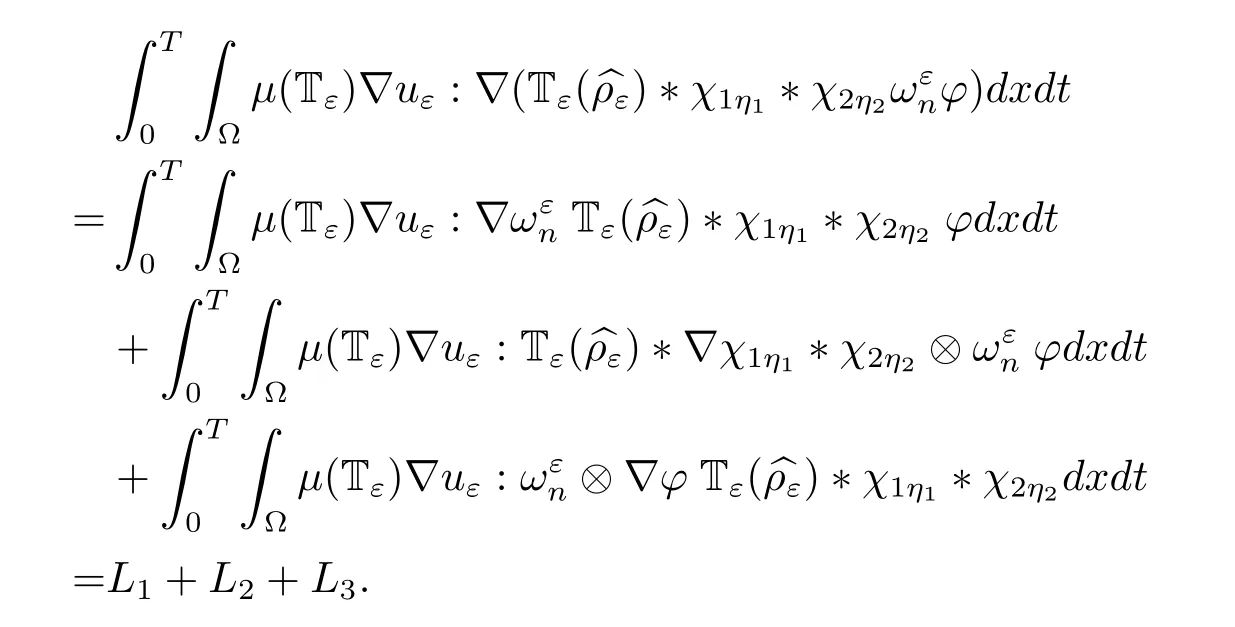
It is easy to check that
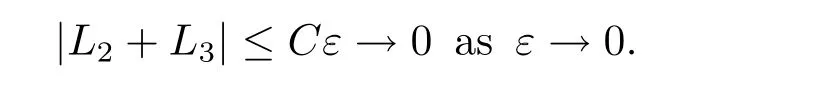
On the other hand,
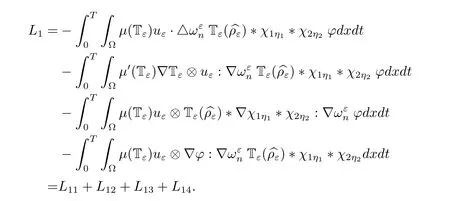
We also have
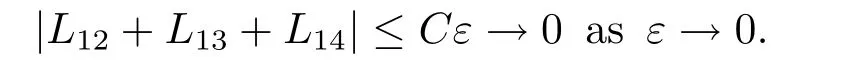
To L11,by virtue of the cell problem,we have

We continue discussing the convergence of those three terms.
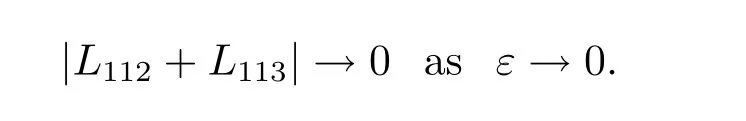
Finally,passing the limit with ε →0,the limit of L111is given by

Let η1,η2→0 and m →+∞and by using the arbitrary property of ?,(3.4),(3.5)and(3.6)lead to the homogenized system of the momentum.That is

Step 3Passing the limit in the energy equation.
Integrating the energy equation in ?×(0,t)and passing the limit,we have

We also have
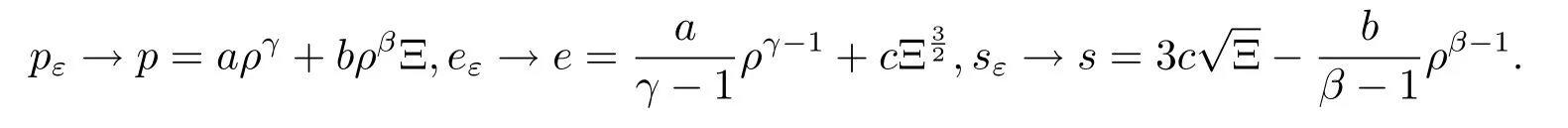
Then the following Gibbs’equation holds
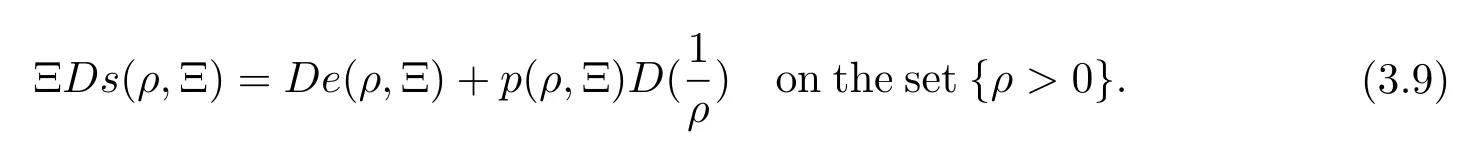
Now we finish Theorem 1.2.

