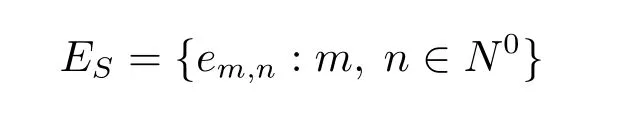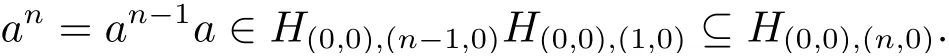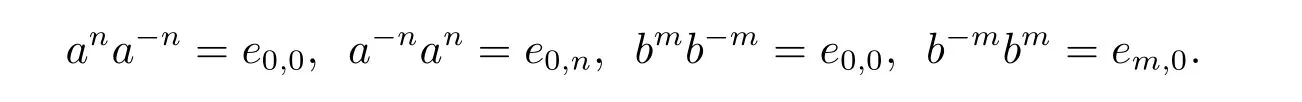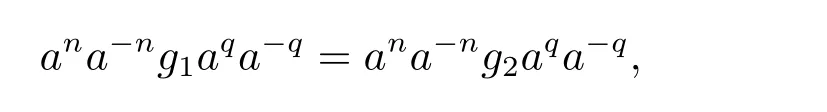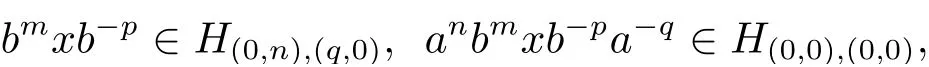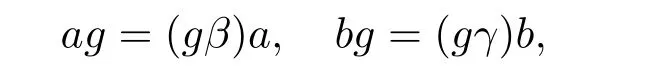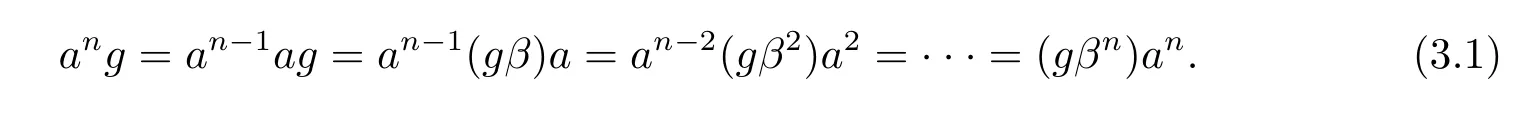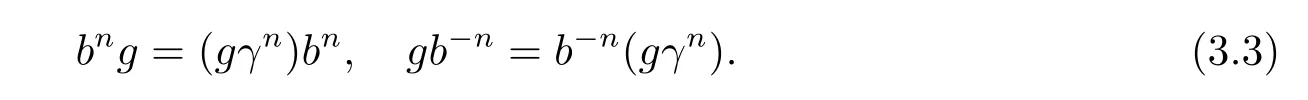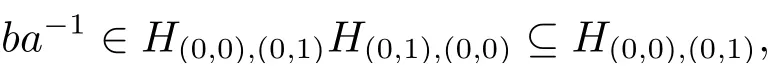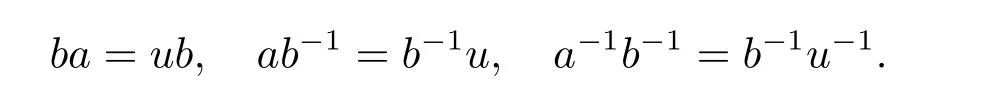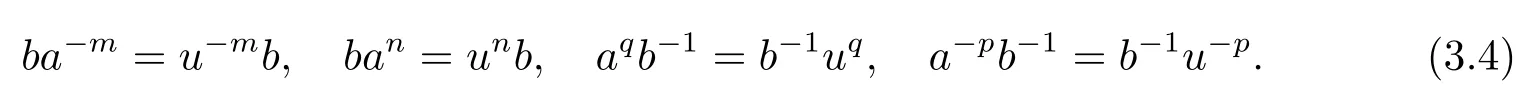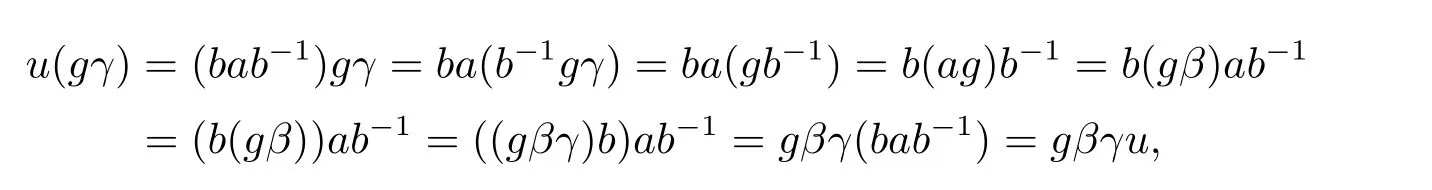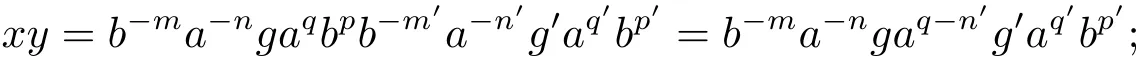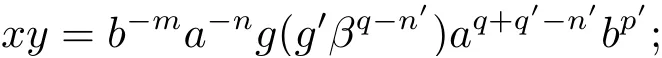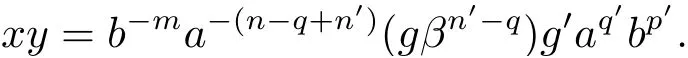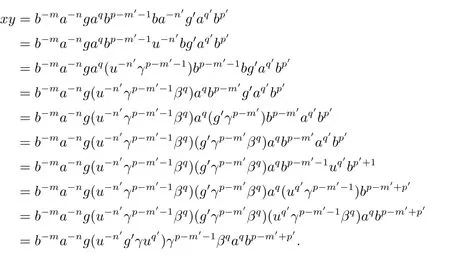正則雙單ω2-半群
汪立民,商 宇,馮瑩瑩
(1.華南師范大學數學科學學院,廣東廣州510631)
(2.普洱學院數學與統計學院,云南普洱665000)
(3.佛山科學技術學院數學系,廣東佛山528000)
1 引言及背景知識
在文獻[1]中,通過對群G 進行Bruck-Reilly 擴張,Reilly 獲得了正則雙單ω-半群的BR(G,θ)結構.Warne 研究了正則雙單ωn-半群,他在文獻[2]中證明了正則雙單ωn-半群具有(G×Cn,?)的結構,其中G 為群,Cn為2n-循環半群,“?”是一種乘法.本文將用文獻[1]的方法研究正則雙單ω2-半群.在本節中,引入了ω2-鏈;在第2 節中,將引入幺半群T 的一種廣義Bruck-Reilly 擴張,然后通過群G 的關于它的兩個同態β,γ 及它的一個元u 的廣義Bruck-Reilly 擴張,得到正則雙單ω2-半群;在第3 節中,將證明任意一個正則雙單ω2-半群都可以這樣構造.
我們將使用文獻[3,4]的概念及記號,其余相關概念參見文獻[3–16].在本文中,映射作用在元素上都統一用映射寫在元素的右側來表示.設a,b 為半群S 的元,若S1a=S1b,則稱a,b 是L-相關的.若aS1=bS1,則稱a,b 是R-相關的.規定H=L ∩R 且D=L ∨R.可知L,R,H 和D 是S 上的等價關系且滿足H ?L ?D,H ?R ?D 及D=L ?R=R ?L.為了避免混淆,記S 上的關系K 為K(S).用La記S 上包含a 的L-類,Ra記S 上包含a的R-類.若半群S 只含一個D-類,則稱它是雙單的.若對半群S 的任一元a,存在唯一的S 的元x,滿足axa=a 且xax=x,則稱半群S 為逆半群,稱x 為a 的逆元,記為a?1.用ES表示半群S 的冪等元的集合.在ES上定義偏序“≤”為e ≤f 當且僅當ef=fe=e.設S 為半群且Cω={e0,e1,e2,···},其中e0,e1,e2,···為冪等元且e0>e1>e2>···,若則稱S 為ω-半群.用N 0 表示所有非負整數的集合,N 表示所有正整數的集合,T 為具有單位元e 的幺半群,θ 為從T 到T 的單位的群He的同態.在上規定乘法為
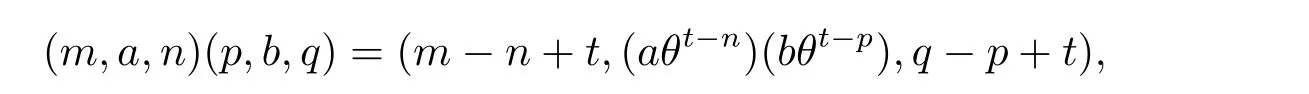
其中t=max{n,p},θ0為T 的恒等映射,則在上述乘法下構成一個半群,稱為T 的由θ 決定的Bruck-Reilly 擴張,記為BR(T,θ),可知

引理1.1[3]設G 為群,θ 為G 的自同態,S=BR(G,θ)為G 的由θ 決定的Bruck-Reilly擴張,則S 為雙單逆ω-半群.反之,任一個雙單逆ω-半群同構于某一個BR(G,θ).
定義1.2在集合上規定一個序為:(m,n)≤(p,q)當且僅當m>p,或m=p且n ≥q,則稱具有這樣序的集合為一個ω2-鏈,記為Cω2.任一個序同構于Cω2的偏序集也稱為ω2-鏈.
若半群S 的冪等元集ES序同構于Cω2,則稱S 為ω2-半群.因此,若S 為ω2-半群,則ES={em,n:m,n ∈N0},其中em,n≤ep,q當且僅當(m,n)≤(p,q).用Rm,n表示S 的包含冪等元em,n的R-類,用Lm,n表示S 的包含冪等元em,n的L-類,用H(m,n),(q,p)表示Rm,n∩Lp,q,即
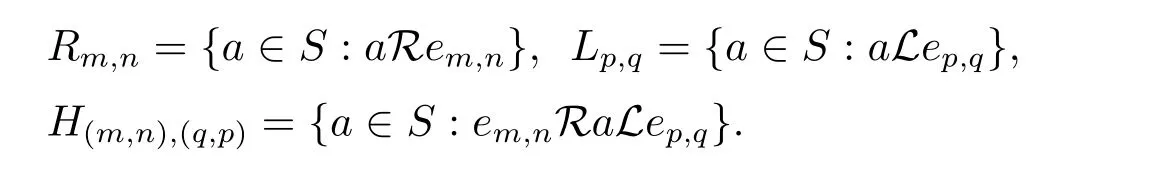
引理1.3[5]設S 為ω2-逆半群,則其中
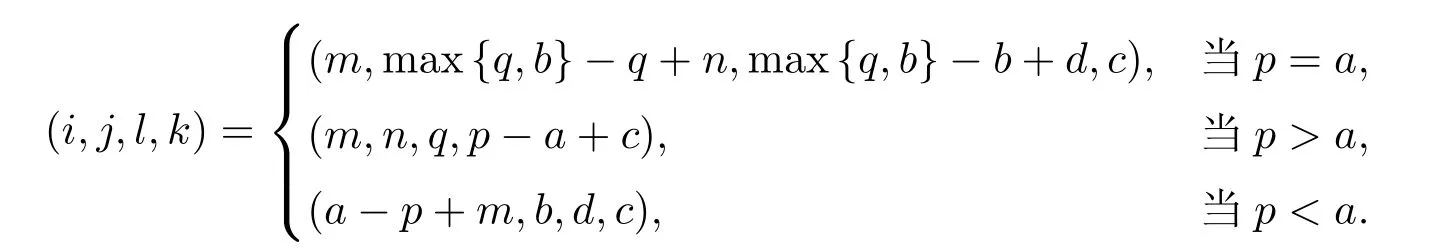
引理1.4設S 為正則ω2-半群,則S 為具有單位元的ω2-逆半群.特別地,雙單ω2-半群是雙單ω2-逆半群.
證 設S 為正則ω2-半群,e 和f 為S 的冪等元,則e ≤f 或f ≤e,從而ef=fe=e或ef=fe=f.不論何種情況,都有ef=fe.因此S 的冪等元可交換,從而S 為逆半群.設ES={em,n:m,n ∈N0},其中em,n≤ep,q當且僅當(m,n)≤(p,q).設a 為S 的任一元,則存在S 的冪等元em,n,使得aa?1=em,n,因此e0,0a=e0,0(em,na)=(e0,0em,n)a=em,na=a.類似有ae0,0=a,于是e0,0是單位元,故S 為具有單位元的ω2-逆半群.
2 廣義Bruck-Reilly 擴張
在這一節中,將引入一種廣義Bruck-Reilly 擴張,對群和它的一對同態做這種擴張,可得到正則雙單ω2-半群.在下一節中,將證明任一個正則雙單ω2-半群都可以這樣構造出來.
設T 為具有單位元e 的幺半群,He為T 的包含e 作為單位元的極大子群,u 為He的一個元,τu為He的內部自同構,即對任意g ∈He,有gτu=ugu?1. 設β,γ 為從T到He的兩個同態,且滿足γτu=βγ,其中β0,γ0為T 的恒等映射,u0=e. 對任意(m,n,t,q,p),(m',n',t',q',p')∈N0×N0×T×N0×N0,在N0×N0×T×N0×N0上規定乘法如下
可以驗證(2.1)式滿足結合律,由于證明過程是直接的和繁瑣的,因此省略了驗證過程.規定從BR(T,γ)到N0×N0×T×N0×N 0 的映射φ 為(m,a,n)φ=(m,0,a,0,n).顯然φ 為單射.對任意(m,0,a,0,n),(m',0,a',0,n')∈N0×N0×T×N0×N0,有
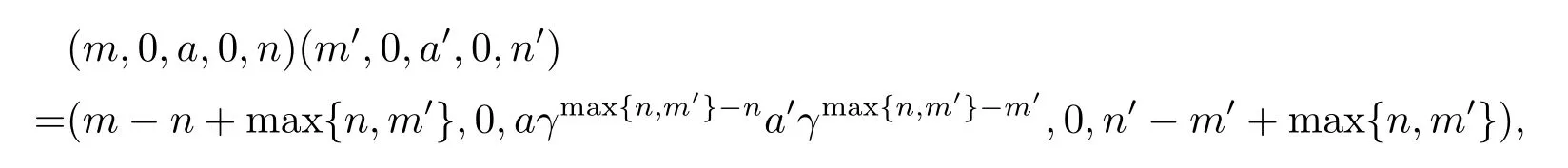
從而φ 為同態. 在這個觀點下,稱上述構造的半群為T 的由β,γ,u 所決定的廣義Bruck-Reilly 擴張,記為GBR(T;β,γ;u).可驗證(m,n,a,q,p)為GBR(T;β,γ;u)的冪等元當且僅當m=p,n=q 且a 為T 的冪等元.
引理2.1設S=GBR(T;β,γ;u)為幺半群T 的由β,γ,u 所決定的廣義Bruck-Reilly擴張,(m,n,a,q,p),(m',n',a',q',p')為S 的任意元,則
(1)(m,n,a,q,p)R(S)(m',n',a',q',p')當且僅當m=m',n=n'及aR(T)a'.
(2)(m,n,a,q,p)L(S)(m',n',a',q',p')當且僅當q=q',p=p'及aL(T)a'.
證(1)設(m,n,a,q,p),(m',n',a',q',p')為S 的兩個元且(m,n,a,q,p)R(S)(m',n',a',q',p'),則存在S 中的元(x,y,b,z,w)使得(m,n,a,q,p)(x,y,b,z,w)=(m',n',a',q',p'),從而
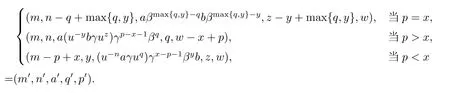
比較第一分量,得m'≥m.對偶地,有m ≥m',從而m=m',因此p ≥x.比較第二分量,得n ≤n'.對偶地,有n ≥n',于是n=n'.若p=x,比較第二分量,得max{q,y}=q,從而

比較第三分量得a'=abβq?y,從而在T 中有Ra'≤Ra.若p>x,比較第三分量,從而在T中有Ra'≤Ra.對偶地,有Ra≤Ra'.故aR(T)a'.
反之,若aR(T)a',則存在T 的元c,d,使得ac=a'且a'd=d,從而
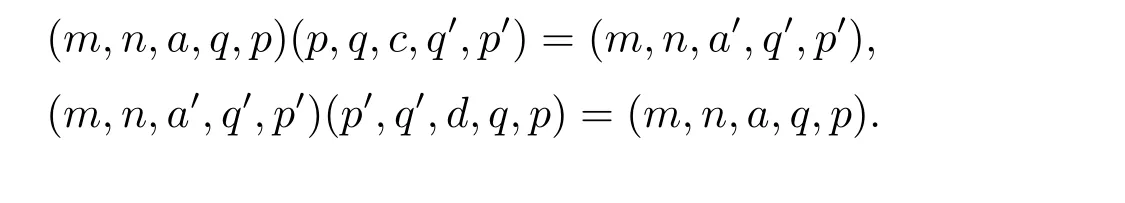
故(m,n,a,q,p)R(S)(m,n,a',q',p').(2)類似可證.
引理2.2設S=GBR(T;β,γ;u)為幺半群T 的由β,γ,u 所決定的廣義Bruck-Reilly擴張,則S 為逆半群當且僅當T 是逆半群.
證若T 為逆半群,則對S 的任一元(m,n,a,q,p),有
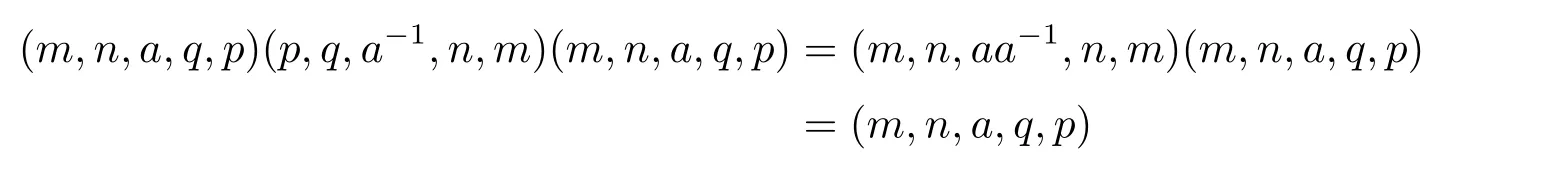
且
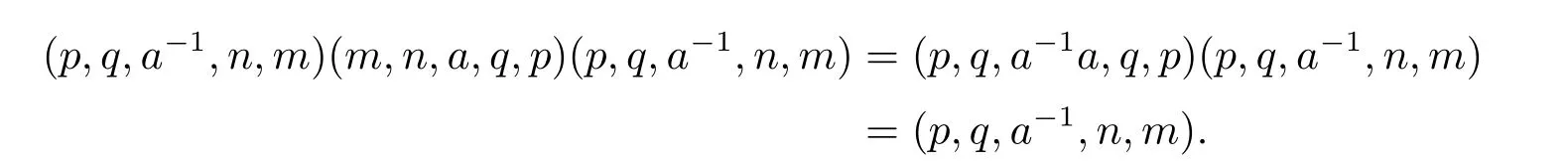
因此(m,n,a,q,p)有逆元(p,q,a?1,n,m),于是S 是正則的.若(m,n,e,n,m)和(m',n',e',n',m')為S 的兩個冪等元,則
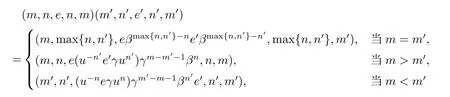
且
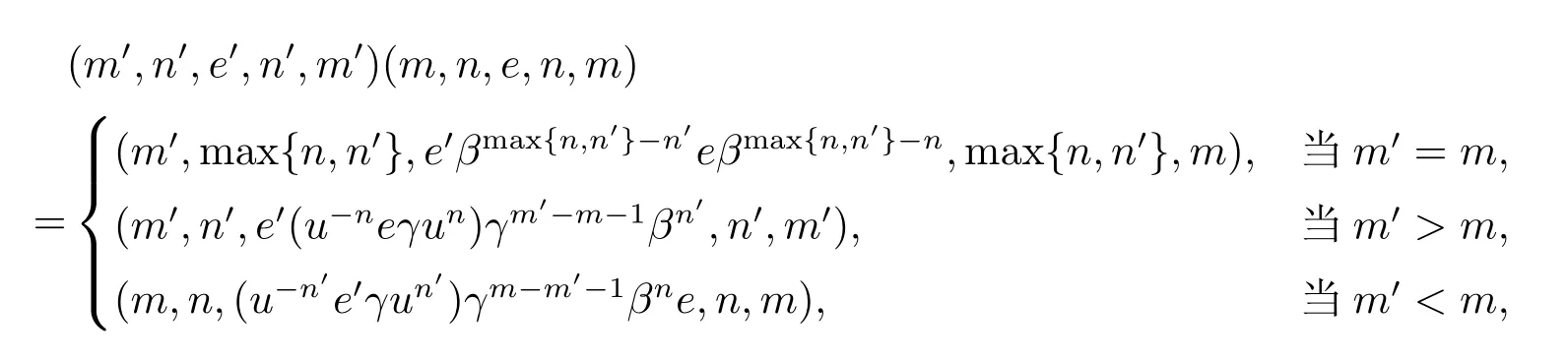
由于T 為逆半群,冪等元可交換,從而S 的冪等元是可交換的.
反之,若S 為逆半群,設(m,n,a,q,p)?1=(x,y,b,z,w),則
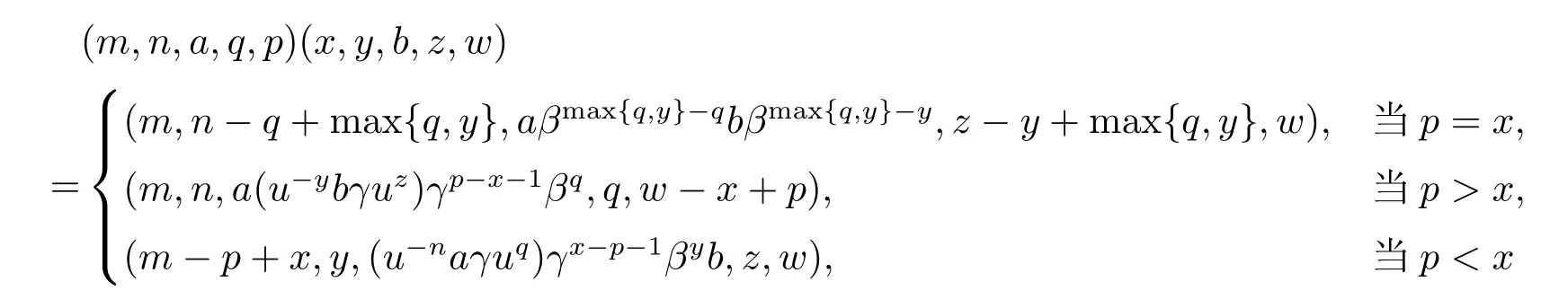
是冪等元且R-相關于(m,n,a,q,p)且L-相關于(x,y,b,z,w),從而p=x.由于
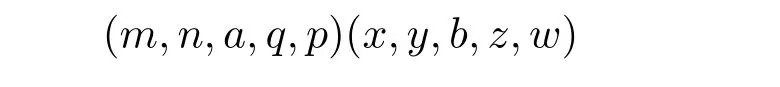
是冪等元,從而m=w 且n=n ?q+max{q,y}=z ?y+max{q,y}=z,因此q=y,于是
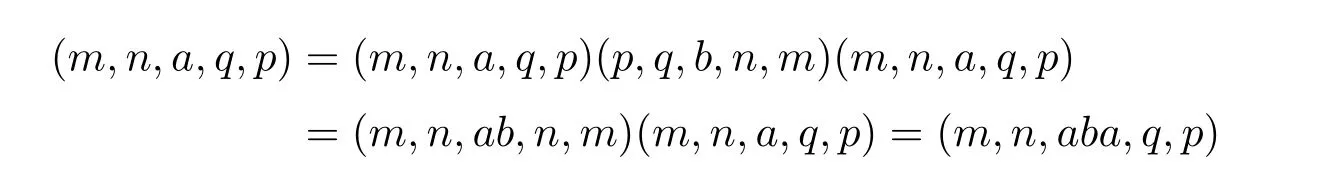
且
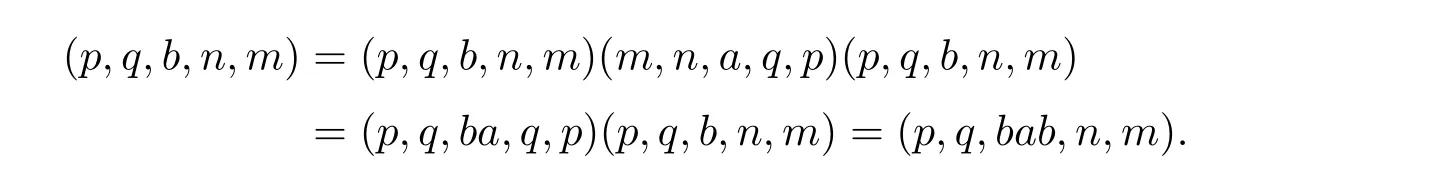
故在T 中有a=aba 且b=bab,從而T 是正則的.若e,f 為T 的兩個冪等元,由于

從而ef=fe.因此T 為逆半群.
定理2.3設G 為群且單位元為e,u 為G 的元,β 和γ 為G 的同態,S=GBR(G;β;γ;u)為G 的由β,γ,u 決定的廣義Bruck-Reilly 擴張,則S=GBR(G;β,γ;u)為正則雙單ω2-半群.
證由引理2.2 知,S 為正則半群.設(m,n,a,q,p),(m',n',a',q',p')為S 的任意兩個元,則

從而(m,n,a,q,p)D(m',n',a',q',p'),因此S 是雙單的.設(m,n,e,n,m),(m,n',e,n',m)為S 的任意兩個冪等元且n 若(m,n,e,n,m),(m',n',e,n',m')為S 的兩個冪等元且m 從而(m',n',e,n',m')<(m,n,e,n,m),因此S 的冪等元構成一個鏈 對任意m,n ∈N0,規定em,n=(m,n,e,n,m),從而S 的冪等元的集合為{em,n:m,n ∈N0}且em,n≤ep,q當且僅當(m,n)≤(p,q).因此S=GBR(G;β,γ;u)為正則雙單ω2-半群. 在本節中,我們將證明任一個正則雙單ω2-半群同構于群G 的由β,γ,u 決定的Bruck-Reilly 擴張GBR(G;β,γ;u). 設S 為正則雙單ω2-半群,ES為S 的冪等元的集合,則 構成ω2-鏈且em,n 從而對任意非負整數n,有an∈H(0,0),(n,0).類似地,設m,n 為非負整數,則 且 由引理1.3,對H(0,0),(0,0)的任意元g,有b?ma?ngaqbp∈H(m,n),(q,p).對任意m,n,p,q ∈N0,規定從H(0,0),(0,0)到H(m,n),(q,p)的對應法則σ 為gσ=b?ma?ngaqbp.若b?ma?ng1aqbp=b?ma?ng2aqbp,則 從而a?ng1aq=a?ng2aq,因此 于是g1=g2.設x 為H(m,n),(q,p)的任意元,則 從而(anbmxb?pa?q)σ=x,因此σ 為雙射. 引理3.1設a ∈ H(0,0),(1,0)且b ∈ H(0,0),(0,1),則S 的任一元都可唯一的表為b?ma?ngaqbp的形式,其中m,n,p,q ∈N0,g ∈H(0,0),(0,0). 設H(0,0),(0,0)=G,g 為G 的任一元,則ag ∈H(0,0),(1,0)H(0,0),(0,0)?H(0,0),(1,0)且bg ∈H(0,0),(0,1)H(0,0),(0,0)?H(0,0),(0,1),從而由引理3.1 知ag 可唯一的表示為b0a0g'a1b0=g'a;bg可唯一的表示為b0a0g''a0b1=g''b,其中g',g''∈G.設β,γ 分別為G 的按如下條件所決定的映射 則 由于aa?1=e0,0且bb?1=e0,0,從而 因此β,γ 為G 的自同態.于是對任意n ∈N0,有 進一步地,由于ga?n∈H(0,n),(0,0)且ana?n=e0,0為S 的單位元,從而 類似地,對任意n ∈N0,有 令u=bab?1,則u?1=ba?1b?1.規定u0=e0,0.由于 從而ba?1=u?1b.類似有 因此,對任意m,n,q,p ∈N0,有 引理3.2設S 為正則雙單ω2-半群,G 為S 的單位的群,a ∈H(0,0),(1,0),b ∈H(0,0),(0,1),則u=bab?1∈G 且γτu=βγ,其中τu為G 的內部自同構,即對任意g ∈G,gτu=ugu?1. 證由知且對任意g ∈G,有 因此對任意g ∈G,有gγτu=ugγu?1=gβγ,于是γτu=βγ. 定理3.3設S 為正則雙單ω2-半群,則SGBR(G;β,γ;u),其中G 為群,β,γ 都為G 的自同態,u ∈G. 證設G,β,γ,u 如前述所規定.由引理3.1 知,S 的每一元都可唯一表示為b?ma?ngaqbp的形式,其中m,n,p,q ∈N0,g ∈G.設x=b?ma?ngaqbp,y=b?m'a?n'g'aq'bp',其中g,g'∈G.分以下三種情形. 情形1若p=m',則 若q=n',則 若q>n',則由(3.1)式知 若q 情形2若p>m',則由(3.1),(3.3),(3.4)式知 情形3若p 因此從S 到GBR(G;β,γ;u)的映射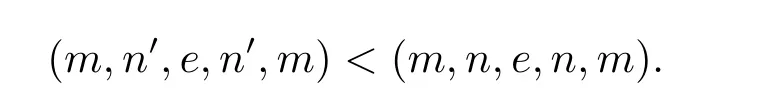
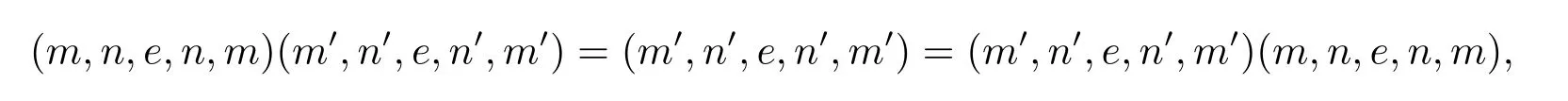
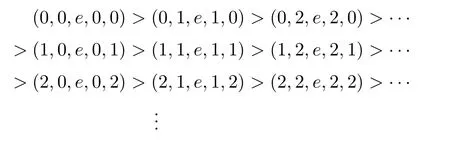
3 結構定理