里程儀輔助捷聯慣導系統的旋轉式行進間對準方法

江一夫，師為建

（中國航天科技集團第十六研究所,西安710100）

0 引言

行進間對準能夠有效提高捷聯慣導武器系統平臺的快速反應能力和機動性能，具有很高的軍事應用價值。根據計算方法的不同，行進間對準方法可分為直接計算姿態的解析對準法、在經典控制方法框架下把對準過程近似解耦為調平回路和尋北回路的羅經對準法[1]、使用狀態估計方法求解姿態的Kalman濾波對準法[2]。羅經法和Kalman濾波法采用Euler角描述姿態，并選擇迭代的局部線性化近似方法，因此會受到小誤差角的制約。文獻[3]～文獻[6]應用慣性凝固思想解析對準，較好地解決了在動態條件下快速獲取粗略姿態信息的問題，使行進間對準技術的研究不再集中于非線性誤差模型的優化。

無論應用哪種計算方法，行進間對準的極限精度仍然受限于慣性儀表誤差和輔助傳感器誤差。而另一方面，旋轉調制技術開始在準靜態對準領域獲得廣泛的應用，其本質仍然是整周旋轉積分對慣性儀表零偏的平均對消作用。這種原理對運動狀態中的慣導系統依然適用，因此本文將旋轉調制技術延伸到了行進間對準，對消慣性儀表隨機常值零偏，反饋校正輔助傳感器誤差，從根本原理角度提升了行進間對準的極限精度。

本文提出了 “基于慣性凝固思想的q-method優化對準[6]+回溯Kalman濾波[7]”方法，解決了從非零速開始的動態對準問題。基于慣性凝固思想的q-method優化對準方法將慣導系統對準問題等價變換為無窮觀測向量下的姿態優化問題，很好地解決了誤差模型非線性的問題。從原理上而言，無論姿態運動如何，慣性系優化對準方法均能夠在任意運動狀態下快速實現自主對準。但是，慣性系優化對準方法存在不適用于頻繁轉彎軌跡[7]、導航參數不全等弊端。在小角度誤差條件下，Kalman濾波仍然是一種可優先選擇的最小方差意義的估計算法。因此，利用慣性系優化對準期間存儲的原始數據和獲取的初始姿態值回溯到對準起始時刻重新開始Kalman濾波精對準，等效延長對準時間，提高對準精度。

1 旋轉式行進間對準方法

如圖1所示，定義g系為由三軸陀螺敏感軸構成的非正交系，定義g0系（Oxg0yg0zg0）為陀螺正交參考坐標系，xg0軸與陀螺敏感軸xg重合，yg0軸在xgyg平面內，zg0與xg0、yg0構成正交系。在實際情況中，非正交系g與g0系之間存在小角度安裝誤差。定義p系為轉位機構的臺面坐標系，zp與轉位機構的旋轉軸重合，xp與xgo在轉臺臺面上的投影重合，yp與zp、xp構成正交系。對于機抖偏頻激光陀螺慣導系統而言，p系與g0系之間僅存在小角度安裝誤差，可以通過轉位機構的正反整圈旋轉標定得到兩者之間的轉換關系。

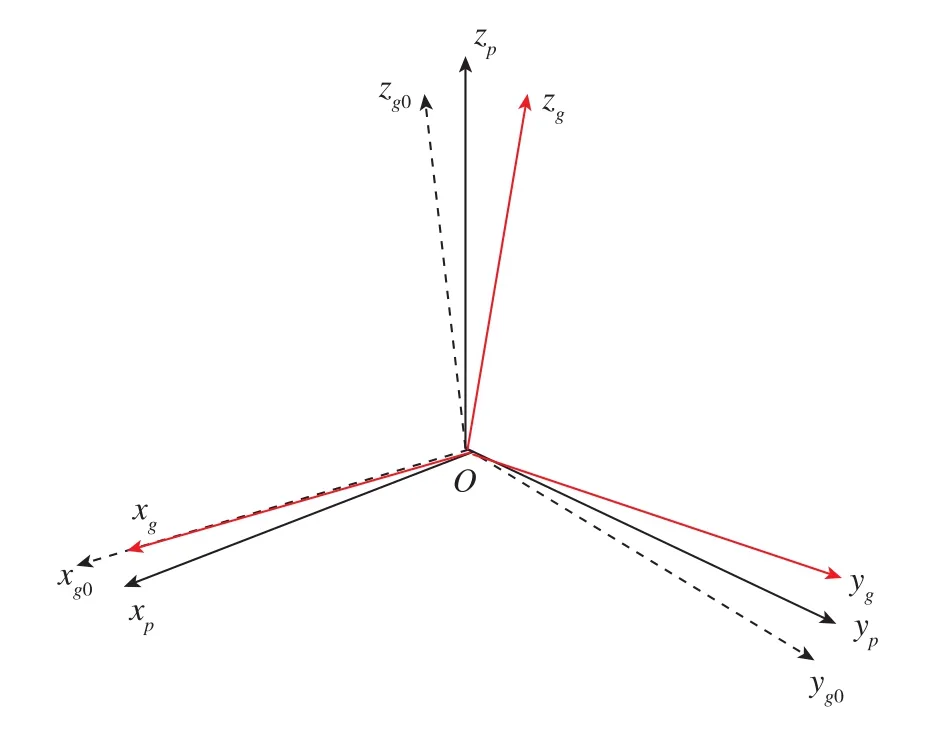
圖1 旋轉式慣導系統中的坐標系關系Fig.1 Coordinates relationship in rotator inertial navigator

圖1中，三個坐標系與轉位機構固聯，隨轉位機構旋轉。設轉位機構在電氣零位時的p系為捷聯慣導載體右前上坐標系b系，在尋北過程中轉位機構繞zp的旋轉角度為?（t），則有

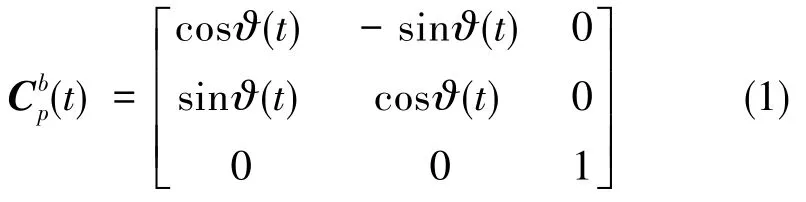
進一步，設當地東北天地理坐標系為n系，里程儀輸出坐標系為車體右前上坐標系m系，其與慣組載體坐標系b系之間存在小角度安裝誤差。如圖2所示，兩個坐標系之間的俯仰安裝偏差角為αθ，方位安裝偏差角為αψ。

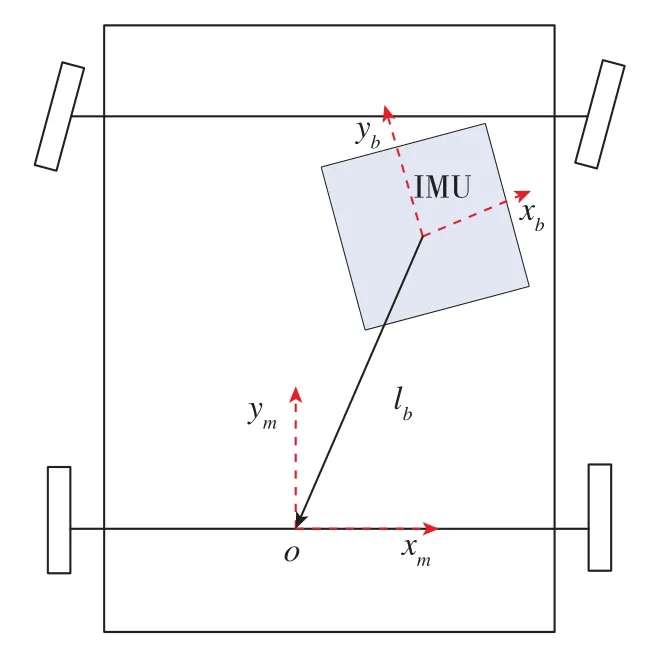
圖2 慣組載體坐標系與車體坐標系的相互關系Fig.2 Relationship between the IMU body frame and the vehicle frame

旋轉式行進間對準采用 “慣性系優化對準+回溯Kalman濾波精對準”方式，如圖3所示。其中，ts為對準開始時間，t1為慣性系解析對準結束時間，te為行進間對準結束時間。從ts時刻啟動旋轉開始，慣性系對準并保存慣性儀表、轉位機構的數據和里程儀脈沖直至t1時刻，然后回溯到ts時刻重新開始進行Kalman濾波對準直至對準結束，以達到等效延長對準時間的目的。

圖3 旋轉式行進間對準方案Fig.3 Scheme of rotatory in-motion alignment

里程儀在已被粗標定的基礎上可以提供車體系m的等效前向速度，其與載體約束信息相結合可以生成三維速度矢量，通過安裝關系和轉位機構測角信息可以將該速度信息轉換到轉位機構臺面坐標系p系中。事實上，由于機抖激光陀螺的數字濾波存在延時，慣性儀表信息與里程儀信息和轉位測角信息是不同步的，但這個延時是固定的，具體延時由數字濾波器的階數和采樣頻率確定。為了簡單可靠地對延時進行補償，本文通過保存后兩者一段時長的數據，實現等效 “延后”組合，待轉位機構停止轉動時輸出對準結果。

慣性儀表的旋轉調制相當于一種誤差自補償措施，可以消除轉軸垂直方向慣性儀表的常值零偏誤差，其短時高精度又可以反饋校正里程儀誤差，最終兩者的誤差可相互校正，實現對準精度的提升。回溯濾波等效延長了對準時間，減小了慣性儀表的隨機游走誤差和里程儀噪聲誤差的影響，確保了行進間對準在不同軌跡下可達到較高的精度。

2 慣性系優化對準

Kalman回溯最優濾波的前提是姿態誤差角已是小角度。為了獲取初始角度，采用基于慣性凝固思想的q-method優化對準方法將慣導系統對準問題等價變換為無窮觀測向量下的姿態優化問題，很好地解決了最優濾波精對準誤差模型非線性的問題。

設慣性空間固聯轉位機構臺面坐標系為p0，慣性空間固聯初始時刻地理坐標系為n0，可將慣性系的比力方程改寫為

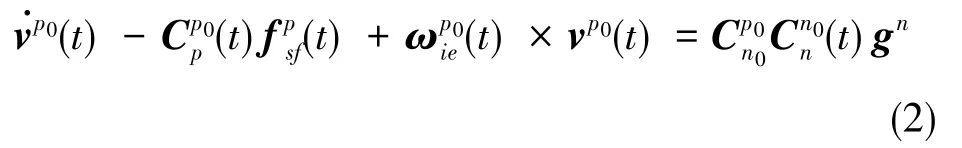
由于里程儀輸出的是里程增量信息，常規動基座算法均對式（2）采取了雙重積分[3，8]。但是，這種方法淹沒了載體部分運動信息，只能適應起始速度為零的動基座對準。若從非零速開始對準，其收斂速度極慢，很多時候甚至不能滿足粗對準的精度要求。因此，對式（2）兩邊只取一次積分，得到兩個矢量的表示形式為

式（3）中，vp為速度信息通過固定安裝關系轉換得到的捷聯慣組坐標系的速度。vp（0）和vp（t）均采用滑動平滑方式進行求取，這種方式既避免了對里程增量求微分而導致的速度噪聲放大，又能實現從任意起始速度開始的行進間對準。載體速度信息輔助行進間對準的計算流程如圖4所示。

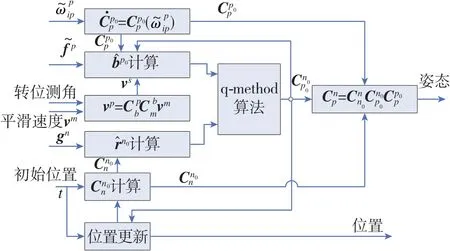
圖4 由載體速度信息輔助的旋轉式慣性系對準算法Fig.4 Inertial freezing algorithm of vehicle-velocity aided rotatory IMA

利用多對觀測矢量，對準問題實質上可以轉換為利用導航參考系和載體系的觀測矢量來確定姿態的問題。解決這一類問題的算法在航天器飛行控制中有著很長的發展歷史，其主要目的是找出滿足如式（5）的正交姿態方向余弦矩陣A。

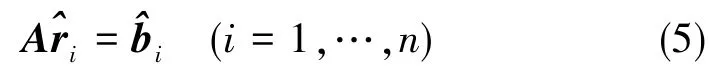
基于矢量觀測的定姿算法主要可分為兩類：確定性算法（一般是指TRIAD算法）和最優定姿算法。其中，最優定姿算法主要為基于Wahba問題的各類最小二乘意義的最優算法，如奇異值分解算法（SVD）、 四元數算法（q-method）及其變形、 快速最優姿態矩陣算法（FOAM）[9]等。由于各類算法種類繁多，綜合考慮精確度、魯棒性、實時遞推性和計算量等性能后，行進間對準選用了Davenport提出的q-method四元數方法。四元數方法可被簡單表述如下：令為各對矢量觀測對應的非負權重，則可認為式（6）的最大正特征值對應的特征向量即為所求的最優姿態四元數。

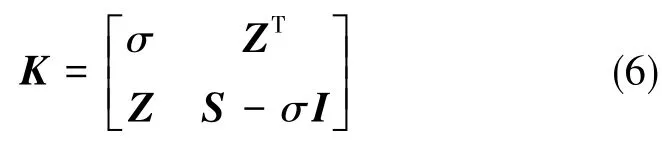
式（6）中，

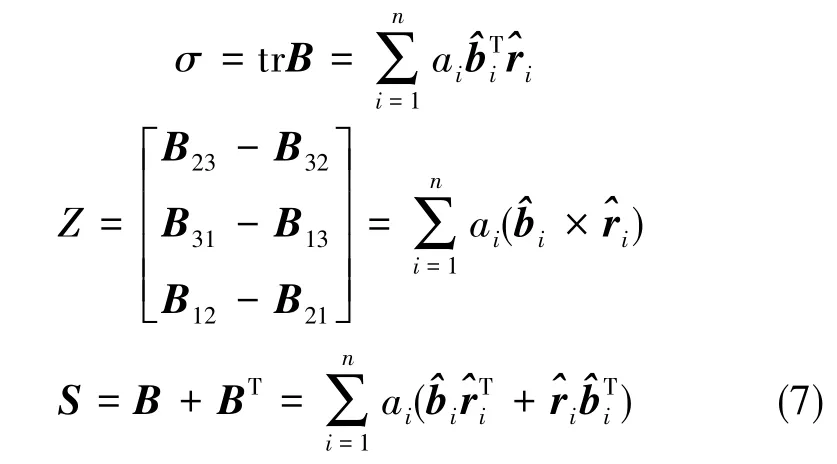
3 回溯Kalman濾波精對準

慣性系優化對準能解決快速粗略姿態的獲取問題，但其存在軌跡適應性差、導航參數不全等弊端。同時，由于里程儀參數不能準確已知且對準算法未對其進行估計，慣性系優化對準算法難以達到高精度水平。在已經獲得粗略姿態角的條件下，Kalman濾波仍不失為一種優先選擇的對準算法。本文利用慣性系優化對準期間存儲的原始數據和獲取的初始姿態值回溯到對準起始時刻重新開始Kalman濾波精對準，同時對里程儀參數進行估計。

綜合里程儀的俯仰、航向安裝偏角估計誤差δαθ、δαψ及標度因數誤差Δfv，慣性自主導航系統的多信息融合濾波器可建立如下18維狀態量

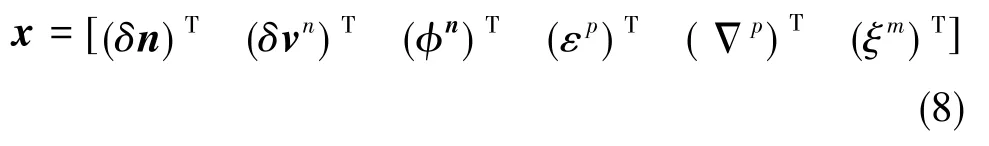
式（8）中，δn=[δrEδrNδrU]為在n系中的計算位置誤差，δvn為地理系的地速誤差，φn為慣組系相對地理系的姿態角誤差，εp和Δp分別為p系的等效陀螺零偏和加速度計零偏，ξm=[δαθδαψΔfv]，δαθ為安裝俯仰偏差角的估計誤差，δαψ為安裝方位偏差角的估計誤差。

結合慣性導航系統通用的擾動誤差模型，可將Kalman濾波系統方程表示為

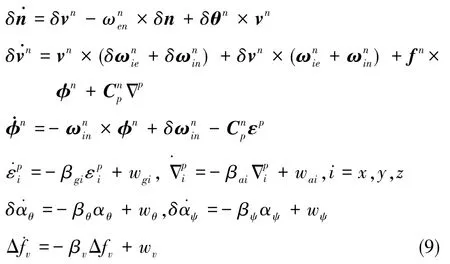
為了避免因長時間導航慣性儀表零偏和里程儀參數估計精度出現 “虛高”的現象，式（9）將慣性儀表零偏和里程儀參數誤差建模為一階Markov過程。其中，β為反相關時間常數，w為Markov過程的激勵噪聲，激勵噪聲均方差q=2βRx（0），Rx（0）為 Markov過程的自相關函數。分別為地理系相對ECEF系的旋轉速率、地理系相對慣性系的旋轉速率和地球自轉速率在地理系上的投影。

由于三軸慣性儀表在旋轉過程中與車體系的里程儀信息進行了組合，因此其必須通過轉換才能進行最優融合。假設車體系m與捷聯慣組系b之間固定安裝偏角的估計誤差矢量為η=[δαθδαγδαψ]，而旋轉的轉位機構臺面坐標系p相對捷聯慣組系b的轉位角度可以通過光電編碼器實時讀取。為了確保測角信息與慣性儀信息的同步，測角信息也經過了同等階數數字濾波器的轉換，具體轉換關系如式（1）所示。量測模型可以表示為

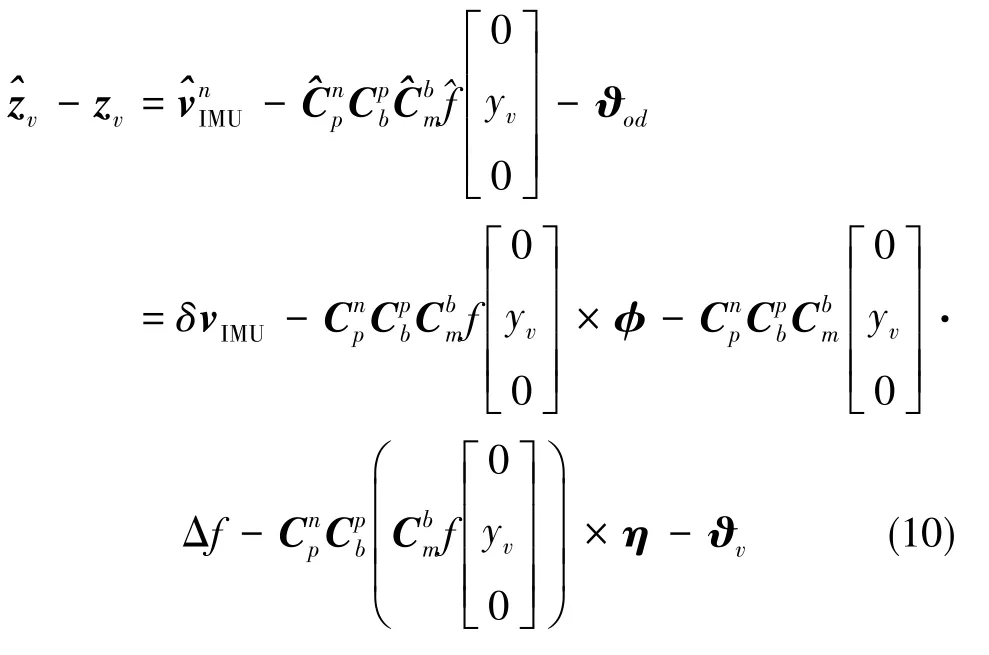
4 仿真及試驗驗證

4.1 仿真分析

針對實際作戰要求進行仿真分析，設置陀螺的等效零偏為 0.005（°）/h（1σ），角隨機游走誤差為0.0008（°）/h1/2，加速度計的等效常值零偏為100μg（1σ），噪聲強度為 10μg，初始地理緯度、 經度和高度分別為34°、108°、380m。里程儀標度因數存在0.1%的初始誤差和隨機誤差，真實俯仰相對安裝角和航向相對安裝角分別為0.7°和0.2°。對 “捷聯式行進間對準”和 “正反旋轉式行進間對準”兩種模式進行仿真，其三軸慣性儀表的真實姿態如圖5和圖6所示。其中，θ、γ和ψ分別為轉位機構臺面坐標系p相對地理系n的俯仰角、橫滾角和航向角。從圖6可以看出，旋轉式行進間對準姿態變化曲線相當于在圖5捷聯式行進間對準姿態變化曲線的基礎上疊加了持續正反旋轉。

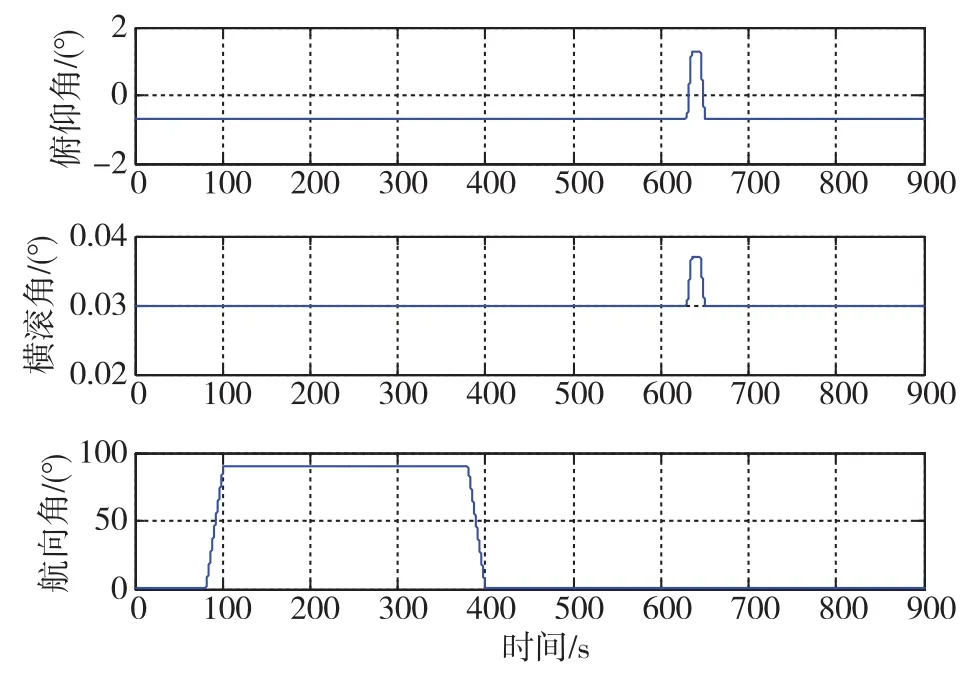
圖5 捷聯式行進間對準的三軸真實姿態曲線Fig.5 Attitude curves during strapdown IMA procedure

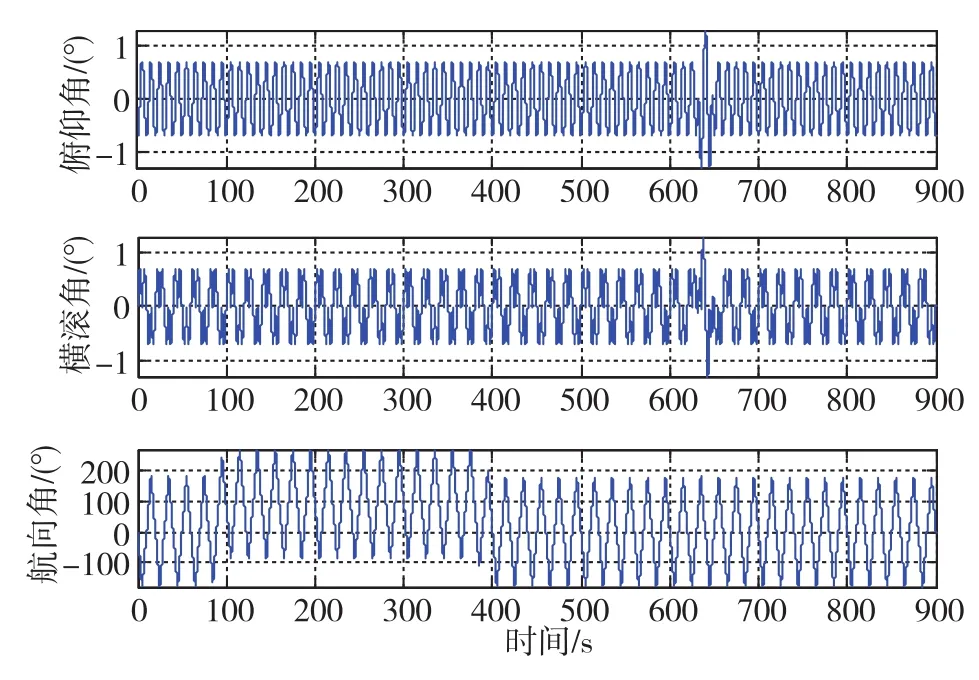
圖6 旋轉式行進間對準的三軸真實姿態曲線Fig.6 Attitude curves during rotatory IMA procedure

捷聯式行進間對準和旋轉式行進間對準的三軸姿態誤差收斂曲線如圖7和圖8所示。其中，δφx、δφy和δφz分別為俯仰角誤差、 橫滾角誤差和航向角誤差。為了對回溯Kalman濾波的優勢進行說明，圖中還比較了慣性系解析算法和回溯Kalman濾波算法的優劣。

從圖7、圖8的仿真結果可以看出，回溯濾波算法明顯優于慣性系解析算法，因為回溯濾波算法大幅加快了對準的收斂速度。無論是捷聯式方案或是旋轉式方案，回溯濾波算法在900s時的對準精度要優于慣性系解析算法。

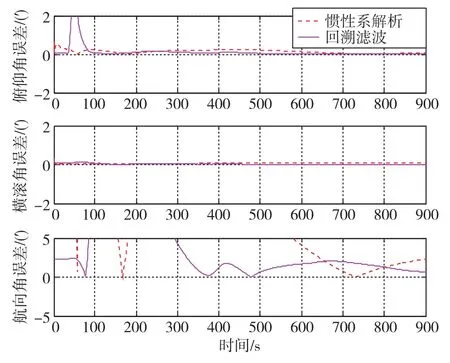
圖7 捷聯式行進間對準姿態誤差收斂曲線Fig.7 Attitude error curves during strapdown IMA procedure

根據文獻[10]中的可觀性分析，捷聯式慣導和里程計組合導航在直線行駛條件下的對準極限精度近似為靜基座對準精度，在轉彎機動下定向極限精度近似為靜基座多位置對準方位精度。因此，根據仿真條件，捷聯式行進間對準在車輛直線行駛時的航向對準極限精度約為1.3′，仿真軌跡存在90°的轉彎機動，航向精度略高于此。在圖7中，最終航向對準精度約為1′。旋轉式行進間對準近似對消了旋轉軸垂直方向的陀螺零偏，只殘留了旋轉軸陀螺零偏投影的等效東向陀螺零偏和隨機誤差，因此可以達到較高精度。在圖8中，最終航向對準精度達到了0.5′。對兩種方案各進行了10次仿真，其俯仰角、橫滾角和航向角的對準結果如表1所示。表1中的航向精度統計結果是相對仿真俯仰角、橫滾角和航向角真值而言的，三者分別為-0.7°、 0.03°和 0.2°。 從表 1中的結果可以看出，捷聯式行進間對準航向精度為1.08′，旋轉式行進間對準航向精度達到了0.54′（RMS），可明顯提高行進間對準精度。

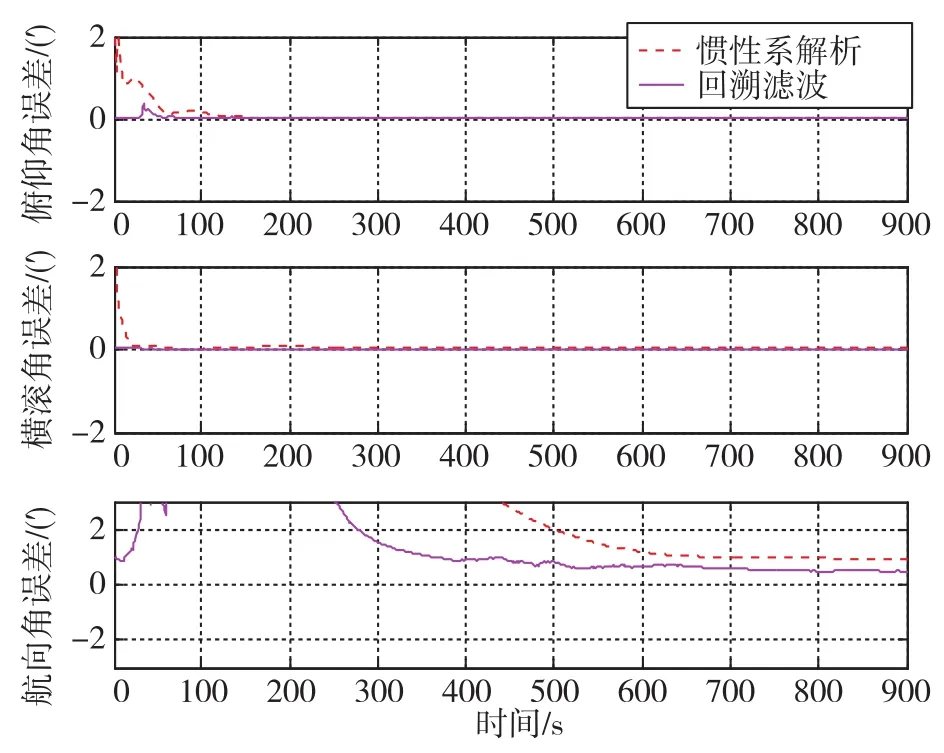
圖8 旋轉式行進間對準姿態誤差收斂曲線Fig.8 Attitude error curves during rotatory IMA procedure

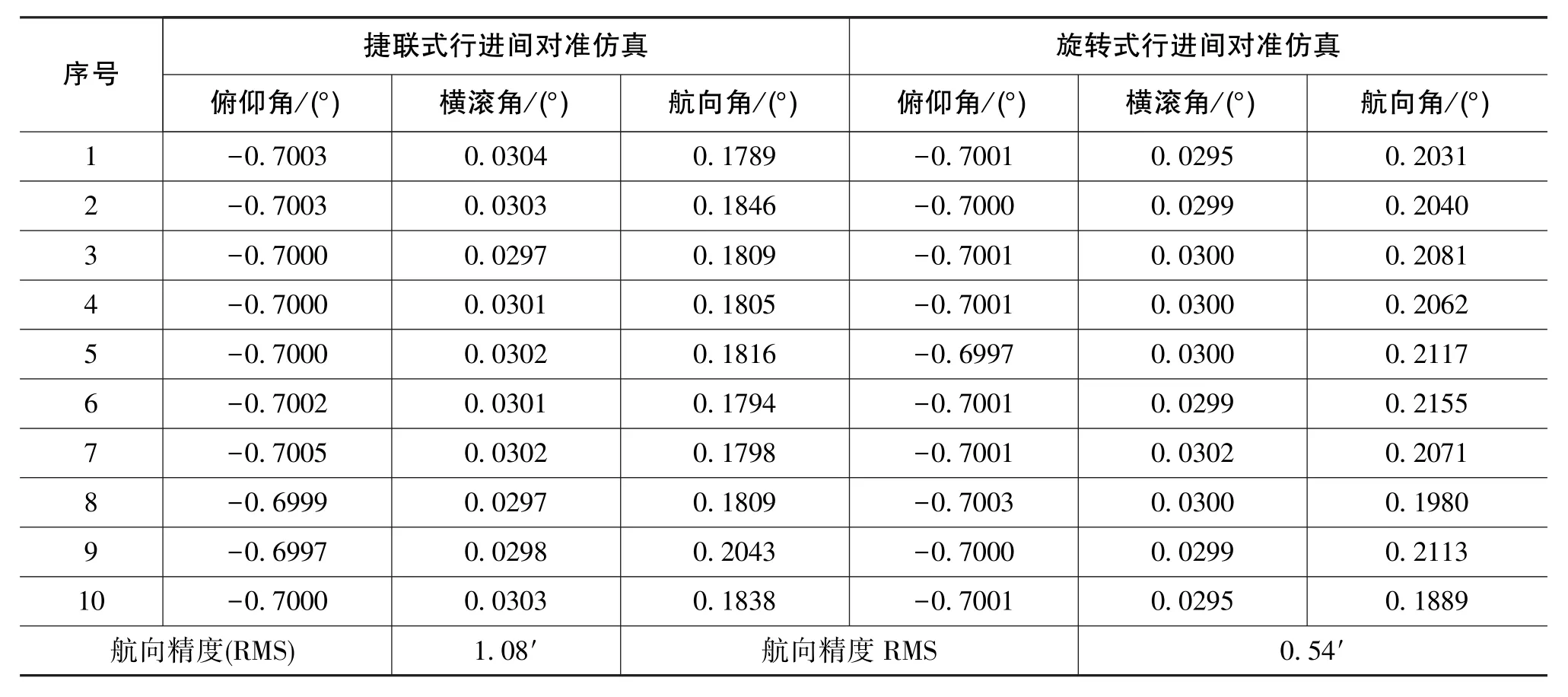
表1 捷聯式和旋轉式行進間對準仿真結果統計Table 1 Statistics of strapdown and rotatory IMA simulation

4.2 試驗驗證

采用陀螺零偏穩定性為 0.005（°）/h（1σ）、 加速度計零偏穩定性為30μg（1σ）的樣機系統進行了旋轉式行進間對準試驗，圖9為駐車對準后純慣性導航姿態結果經轉位測角轉換后的載體航向角變化曲線。旋轉式行進間對準過程待轉位機構停止轉動后，停車記錄相應的三軸姿態結果，并再次進行駐車對準，以之作為參考基準，參考基準的精度可以達到0.4′（RMS）。表2為相應行進間對準結果。由表2可以看出，行進間對準精度能夠達到0.99′（RMS）。由于實際過程中載體水平姿態的變化，等效東向陀螺零偏并不能被抵消完全，同時由行駛路況等因素引起的里程儀標度因數誤差同樣會使量測產生較大誤差，因此實際試驗精度并沒有達到仿真精度。

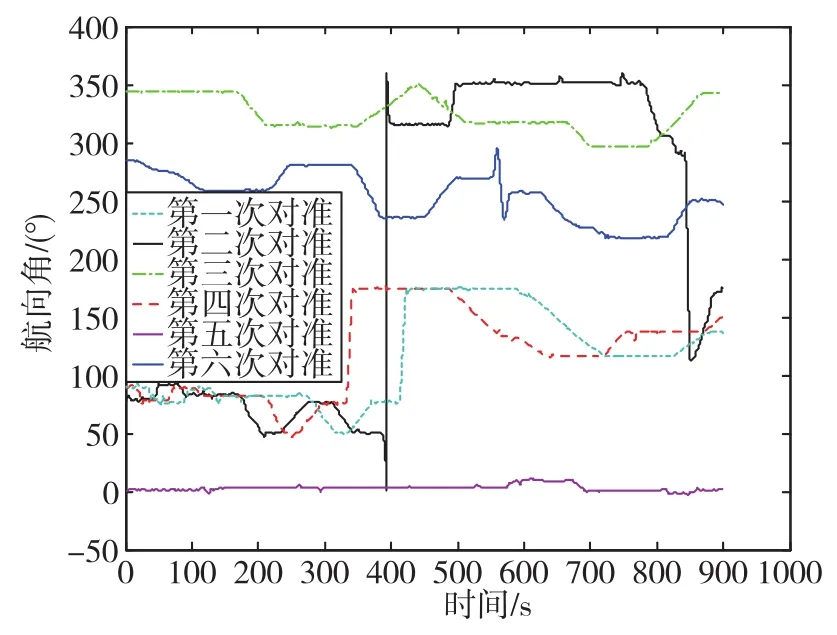
圖9 旋轉式行進間對準試驗慣組載體航向變化曲線Fig.9 Heading curves of IMU during rotatory IMA test

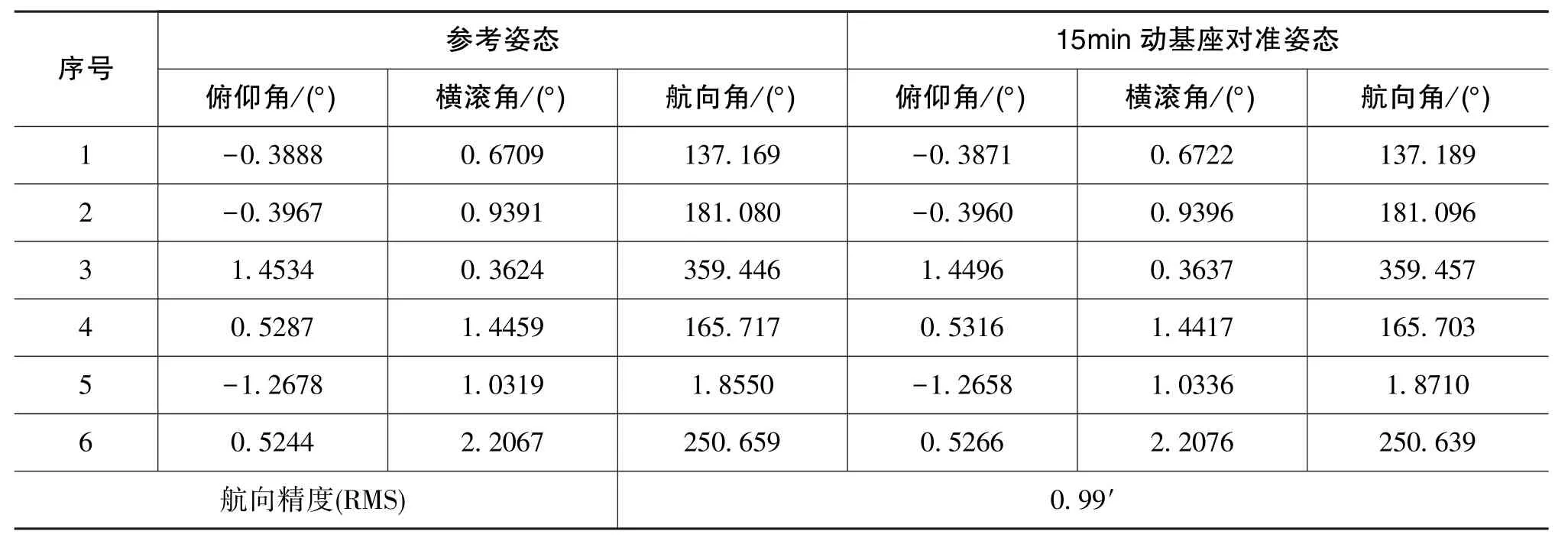
表2 旋轉式行進間對準試驗統計結果Table 2 Statistics of rotatory IMA vehicular test

5 結論

為提高行進間對準的精度和軌跡適應性，將旋轉調制原理引入了行進間對準，提出了 “正反旋轉+慣性系粗對準+回溯Kalman濾波精對準”的對準方案，改進常規慣性系行進間對準算法為基于平滑里程計微分速度的一次積分算法，同時給出了多源自主信息的時間同步措施。仿真和試驗驗證了提出的行進間對準方案，表明旋轉式行進間對準能較大幅度地提升對準精度。