基于CFD的大型立式軸流泵反向發(fā)電穩(wěn)定性能分析
周 穎,鄭 源,何中偉,汪昊藍
(1. 河海大學水利水電學院,江蘇 南京210098;2. 河海大學創(chuàng)新研究院,江蘇 南京210098;3. 中國電建華東勘測設計研究院有限公司,浙江 杭州311100)
1 研究背景
泵站在我國南水北調工程中發(fā)揮著重要的作用,具有排澇防洪,解決農業(yè)用水問題等。部分水泵可進行反向發(fā)電獲得一定的經濟效益,但當水泵在進行反向發(fā)電時,水流流態(tài)受進出水流道的影響,壓力脈動較水泵工況下會發(fā)生一定的改變,嚴重時甚至對廠房結構形成威脅。
對軸流泵壓力脈動及反向運行方式的研究很多。張德勝[1]等通過模型試驗研究了斜流泵葉輪進口段至導葉出口段設置7個壓力脈動處,不同工況下高比轉速斜流泵內部壓力脈動特性和規(guī)律;黎義斌[2]等通過設置壓力脈動監(jiān)測點,研究動靜干涉對混流泵內部流動非定常壓力脈動特性的影響,并進行了試驗與數(shù)值模擬的對比驗證;羅旭[3]等采用CFX軟件對離心泵的內部流場進行數(shù)值模擬,分析其不同監(jiān)測點在不同流量下的壓力脈動特性。施衛(wèi)東[4]等針對軸流泵模型,對不同轉速下的模型進行試驗,分析壓力脈動頻率分布規(guī)律;張德勝[5]等對軸流泵在不同流量工況下的壓力脈動特性進行了試驗研究,分析壓力脈動的位置及頻率分布規(guī)律;楊建東[6]等對水泵水輪機在偏離設置工況下,進行了試驗測量,分析各部分壓力脈動形成的原因;王松林[7]等基于RNG k-ε湍流模型及輸運方程空化模型,對小流量工況離心泵瞬態(tài)空化流動進行數(shù)值模擬,研究壓力脈動在流道不同位置的分布規(guī)律;湯方平[8]等基于RANS方程和RNG k-ε模型,采用Ansys-CFX軟件對軸流泵泵段進行了多工況三維非定常數(shù)值模擬,得到了不同工況下軸流泵內部不同監(jiān)測點的水流壓力脈動值規(guī)律。
前人對于軸流泵抽水時的穩(wěn)定性研究較多,而對泵站反向運行的穩(wěn)定性分析很少。本文通過對泵站流道進行全數(shù)值模擬,并對泵站正轉反轉工況下,在最優(yōu)工況點時,在不同位置產生的壓力脈動規(guī)律進行分析,研究泵反向發(fā)電時的穩(wěn)定性問題。
2 數(shù)值模擬與試驗
2.1 模型建立及網(wǎng)格劃分
如圖1所示,本文結合南水北調東線某泵站進行反向發(fā)電工況的數(shù)值模擬[9]。泵站機組基本參數(shù)如下:正反轉運行轉速均為150 r/min、設計揚程4.70 m,葉輪葉片為3片,安放角為-2°。
因軸流泵結構復雜,采用非結構網(wǎng)格對計算區(qū)域進行網(wǎng)格劃分,對轉輪部分及導葉部分進行加密。對網(wǎng)格進行無關性驗證[10]后最終確定方案劃分網(wǎng)格總數(shù)為250萬,其中轉輪體網(wǎng)格總數(shù)為103萬,導葉體97萬。
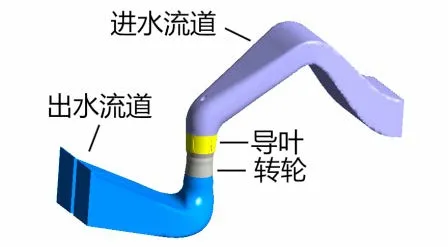
圖1 流道整體圖
2.2 基本控制方程
流體基本控制方程采用基于Reynolds平均的Navier-stokes方程[10],如公式(1)所示:
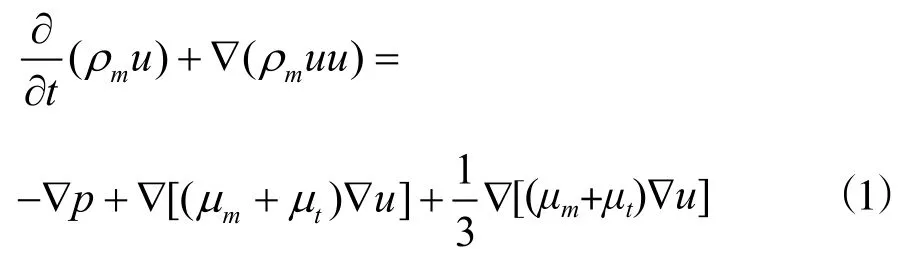
其中t為時間;ρm為混合項的密度;μt為湍流粘性系數(shù);μm為動力粘性系數(shù),按汽,液兩相體積分數(shù)加權平均后獲得;p為壓力;u為速度矢量。
3 邊界條件及試驗
3.1 壓力脈動監(jiān)測點布置
如圖1所示,在轉輪進出口截面設2個監(jiān)測面,兩監(jiān)測面距離為2.2 m。為研究監(jiān)測面壓力脈動分布規(guī)律,徑向設置A1~A3,B1~B3三個監(jiān)測點;周向設置A2,A4,A5及B2,B4,B5三個監(jiān)測點,監(jiān)測點分布如圖2所示。
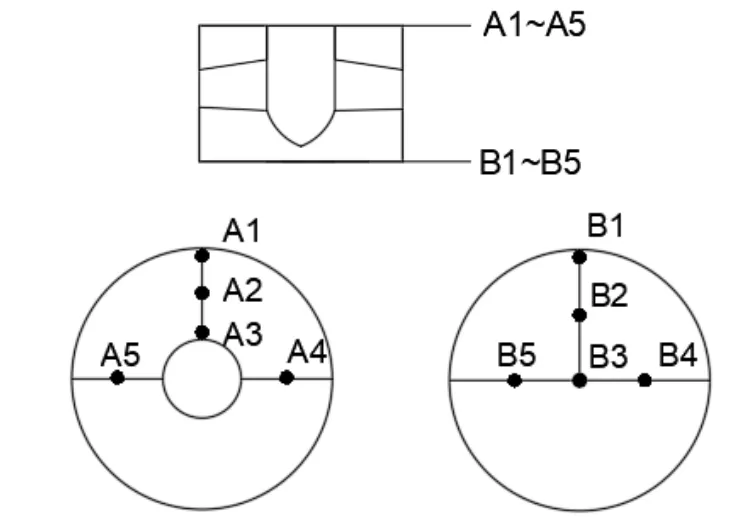
圖2 監(jiān)測面及監(jiān)測點示意圖
為研究轉輪前后壓力脈動規(guī)律,需進行非定常計算[11]。非定常計算以定常計算為初場,定常計算時設置動靜交接面為冷結轉子類型frozen rotor interface,非定常計算設置動靜交接面為瞬態(tài)凍結轉子類型transient rotor,轉輪邊界均采用壓力進出口[12]。湍流模型選取為SSTk-ε,采用自動壁面函數(shù),固體面設置為無滑移,湍流粘度項采用二階迎風格式,在時間域上采用二階全隱式進行離散[13],為確保進行壓力脈動計算時非定常結果的穩(wěn)定性,設置總的采樣時間為10個周期,設置時間步長為0.001 s,收斂殘差為10-5,選取計算最后2個周期各點監(jiān)測數(shù)據(jù)分析壓力脈動規(guī)律[14]。
3.2 試驗驗證
圖3為河海大學水力機械多功能試驗臺,軸流泵反向發(fā)電試驗在此進行。試驗臺按照《SL140-2006水泵模型及裝置模型驗收試驗規(guī)程》進行設計與建造,試驗綜合不確定度≤0.4%。
在軸流泵轉輪葉片安放角為0°時,采用現(xiàn)場試驗及數(shù)值模擬的方法,通過不斷改變流量得到水泵的外特性曲線(見圖4)。總體看來試驗結果與數(shù)值模擬結果誤差較小,流量-揚程曲線及流量效率曲線與試驗結果較好地吻合,2條曲線趨勢保持一致,驗證了數(shù)值模擬的準確性。

圖3 試驗臺

圖4 軸流泵外特性圖
4 結果分析
4.1 壓力脈動時域圖分析
通過數(shù)值計算得到軸流泵處于水泵反向發(fā)電工況時內部各監(jiān)測點壓力脈動的時域信息[16]。為了消除監(jiān)測點本身的靜壓對該點壓力脈動的影響,在分析中引入無量綱的壓力脈動系數(shù)CP,其表達式為
式中CP為無量綱的壓力系數(shù);Pi為監(jiān)測點在某一時刻的靜壓值,單位Pa,Pave為一個轉動周期內靜壓的平均值,單位Pa。
在水泵及水輪機兩個工況下,對轉輪前后的壓力脈動規(guī)律進行時域圖分析(見下頁圖5)。
圖 5(a)和圖 5(b)為水泵工況下,轉輪進口截面徑向和周向壓力脈動時域圖。B1,B2,B3沿輪緣至轉輪輪轂分布,此時水流受轉輪轉動影響上吸,因受轉輪轉動的影響加劇及導葉與轉輪間的動靜干涉作用強烈,三點處壓力脈動呈現(xiàn)周期性波動,在一個周期0.4 s內有三個明顯的波峰波谷。因轉輪邊緣處間隙較小,水流變化劇烈,B1處為壓力脈動值最大約為0.05,約為B3近輪轂處的5倍。B2,B4,B5為水流中間周向分布的三點,因水流流動比較均勻,三點壓力脈動規(guī)律明顯,幅值相近。圖5(c)和圖5(d)為水泵工況下,轉輪出口截面徑向和周向壓力脈動時域圖。A1,A2,A3沿輪緣至轉輪輪轂分布。此時水流從轉輪流出,仍受轉輪轉動影響,一個轉輪周期內有三個明顯的波峰波谷,三點壓力脈動較轉輪進口處明顯增大,邊緣處A1處水流壓力脈動幅值約為轉輪進口處的2倍。三點壓力脈動幅值從邊緣至輪轂逐漸減小,A1邊緣處壓力脈動幅值約為0.1,約為輪轂邊緣處2倍。
圖 5(e)和圖 5(f)水輪機工況下,轉輪進口截面徑向和周向壓力脈動時域圖。B1,B2,B3沿輪緣至轉輪輪轂分布,此時水流從原出水流道進入,三點壓力脈動規(guī)律明顯。因轉輪邊緣處及中部水流速度變化劇烈,中心處水流影響較小,反映在A1,A2壓力脈動系數(shù)較大達0.06,約為A3處壓力脈動系數(shù)為0.02的3倍。徑向方面,水流從流道較平穩(wěn)地進入轉輪,受轉輪轉動影響,B2,B4,B5三點的壓力脈動規(guī)律明顯且壓力脈動幅值接近。圖5(g)和圖5(h)水輪機工況下,轉輪出口截面處徑向和周向壓力脈動時域圖。水流經過轉輪轉動流出,徑向方面,水流受轉輪轉動影響較大,轉輪邊緣處間隙水流變化劇烈,邊緣處測點B1的壓力脈動值進一步增大達0.15,轉輪中部點B2壓力脈動系數(shù)值達0.06,兩點呈現(xiàn)周期性波動,轉輪中心B3處壓力脈動規(guī)律不明顯。周向方面,水流較均勻地流出轉輪,B2,B4,B5三點受轉輪轉動影響,周期性明顯,三點壓力脈動幅值接近約為0.06。
比較水泵及水輪機兩工況壓力脈動,出轉輪截面水流各點壓力脈動較進轉輪截面壓力脈動值增大,受轉輪轉動影響,水流在轉輪邊緣處速度變化大,壓力脈動劇烈;受進出水流道設置限制,水輪機工況下水流的壓力脈動較水泵工況下壓力脈動值偏大。
4.2 壓力脈動頻域圖分析
在水泵及水輪機兩個工況下,對轉輪前后的壓力脈動規(guī)律進行頻域圖分析。
圖 6(a)和圖 6(b)為水泵工況下,轉輪進口截面徑向和周向壓力脈動頻域圖。B1,B2,B3沿輪緣至轉輪輪轂分布,B2,B4,B5三點在水流中間周向分布。從圖中可以看出水流受轉輪轉動影響嚴重,壓力脈動主要分布在低頻區(qū)域,主頻為轉頻7.5 Hz。輪緣B1處壓力脈動系數(shù)值最大為0.15,從輪緣至輪轂依次減小。水流受轉輪轉動影響較均勻地上吸,B2,B4,B5 壓力脈動系數(shù)幅值接近約為 0.06。圖 6(c)和圖6(d)為水泵工況下,轉輪出口截面徑向和周向壓力脈動頻域圖。可以看出各監(jiān)測點較轉輪進口壓力脈動系數(shù)增加,邊緣處A1的壓力脈動系數(shù)最大達0.32,周向方面A2.A4.A5三點壓力脈動系數(shù)幅值約為0.16。受轉輪轉動影響,壓力脈動主頻仍為轉頻 7.5 Hz,次頻為 2.5 Hz。
圖 6(e)和圖 6(f)水輪機工況下,轉輪進口截面徑向和周向壓力脈動頻域圖,圖6(g)和圖6(h)為轉輪出口截面處徑向和周向壓力脈動頻域圖。水流從原出水流道流入,進出口均受轉輪轉動影響,壓力脈動主要集中在低頻區(qū)域,主頻為轉頻7.5 Hz,次頻為轉頻2.5 Hz,在轉頻倍數(shù)處也有一定的壓力脈動,并逐漸減小。進口截面壓力脈動系數(shù)最大值出現(xiàn)轉輪邊緣處A1,值約為0.3,是轉輪邊緣A3處的3倍。出口截面壓力脈動系數(shù)最大值出現(xiàn)在轉輪邊緣處B1,其值達0.8。周向方向,水流從轉輪較均勻進入與流出,兩監(jiān)測面監(jiān)測點的幅值大小接近,出轉輪時各點的壓力脈動系數(shù)幅值較進轉輪時增大。
比較水泵及水輪機工況,受轉輪轉動影響強烈,各點的壓力脈動頻率分布在低頻,主頻為轉頻,出轉輪時各點壓力脈動幅值較進轉輪時壓力脈動幅值增大,水流在轉輪間隙處變化劇烈,邊緣處監(jiān)測點壓力脈動幅值較大。
5 結論
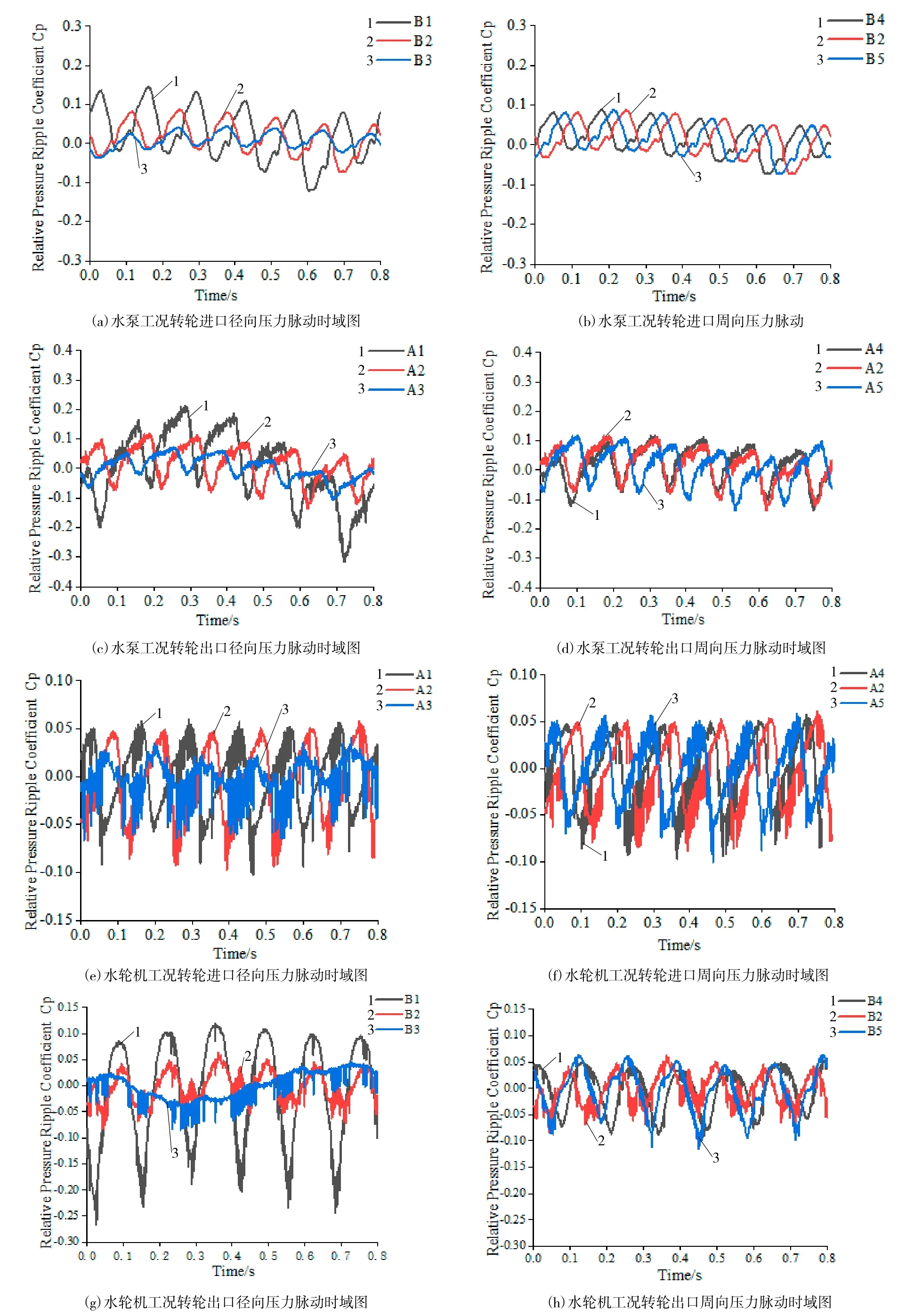
圖5 壓力脈動時域圖
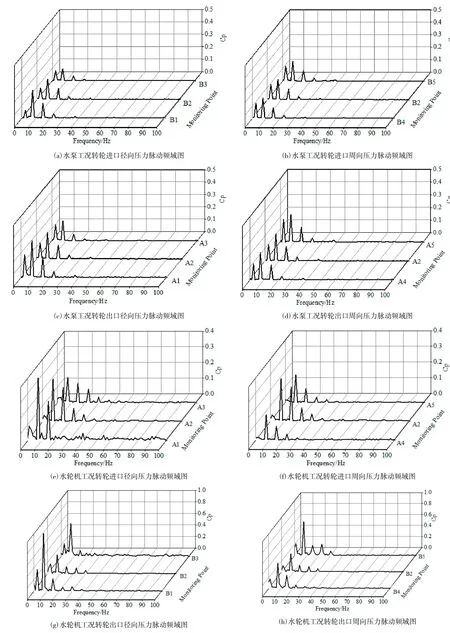
圖6 壓力脈動頻域圖
通過對南水北調蘇北某泵站的機組軸流泵反向發(fā)電工況下的數(shù)值模擬,對機組反向發(fā)電穩(wěn)定性進行了研究。
通過在導葉、轉輪前后設置了徑向與周向監(jiān)測點,對軸流泵的內部運行的穩(wěn)定性進行了模擬分析。水輪機工況下,壓力脈動受轉輪轉動頻率影響明顯,壓力脈動主頻為轉頻;葉輪出口壓力脈動大于葉輪進口處壓力脈動,其壓力脈動幅值約為進口處的2倍,壓力脈動相對值從輪轂到輪緣處逐漸增大。比較水泵工況及水輪機工況下各點的壓力脈動,水輪機工況下各監(jiān)測點均高于水泵工況下各點壓力脈動幅值,機組較水泵工況下振動增加,機組的不穩(wěn)定性增加。

