二維Logistic分數階微分方程的離散化過程

劉杉杉 高飛 李文琴

摘 要：針對二維Logistic分數階微分方程的求解問題，引進了一種離散化方法對其進行離散求解。首先，將二維Logistic整數階微分方程推廣到分數階微積分領域;其次，分析相應具有分段常數變元的二維Logistic分數階微分方程并應用提出的離散化方法對模型進行數值求解;然后，根據不動點理論討論該合成動力系統不動點的穩定性，給出了在參數空間內二維Logistic分數階系統發生第一次分岔的邊界方程;最后，借助Matlab對模型進行數值仿真，并結合Lyapunov指數、相圖、時間序列圖、分岔圖探討模型更多復雜的動力學現象。仿真結果顯示，所提方法成功對二維Logistic分數階微分方程進行離散。

關鍵詞：二維Logistic微分方程;時滯;分段常數變元;不動點;分岔;混沌

中圖分類號： TP391.9; TP301.5

文獻標志碼：A

Abstract： Focusing on the problem of solving coupled Logistic fractional-order differential equation， a discretization method was introduced to solve it discretly. Firstly， a coupled Logistic integer-order differential equation was introduced into the fields of fractional-order calculus. Secondly， the corresponding coupled Logistic fractional-order differential equation with piecewise constant arguments was analyzed and the proposed discretization method was applied to solve the model numerically. Then， according to the fixed point theory， the stability of the fixed point of the synthetic dynamic system was discussed， and the boundary equation of the first bifurcation of the coupled Logistic fractional-order system in the parameter space was given. Finally， the model was numerically simulated by Matlab， and more complex dynamics phenomena of model were discussed with Lyapunov index， phase diagram， time series diagram and bifurcation diagram. The simulation results show that， the proposed method is successful in discretizing coupled Logistic fractional-order differential equation.

Key words： coupled Logistic differential equation; time delay; piecewise constant argument; fixed point; bifurcation; chaos

0 引言

混沌被認為是繼量子力學與相對論之后的第三大科學發現。混沌系統是非線性動力學映射主要表現形式之一，具有良好的類隨機、非周期、對初始值敏感、歷經各態并可確定等特性[1-4]。其中Logistic混沌系統是May[5]在《Nature》上發表的一篇影響甚廣的綜述中提出來的，后來Feigenbaum[6]指出Logistic是通過倍周期分岔到達混沌的。之后，眾多學者一直致力于Logistic的相關研究[7-9]。在此基礎上，研究者們又研究了二維Logistic映射的分岔特性和混沌現象及其在生態學等領域的應用[10-11]。因在對一維映射到高維的研究中，二維Logistic映射起著銜接作用，且對二維映射中混沌現象和混沌控制的研究有助于認識和控制更復雜的高維動力系統的性態[12]，故引起了各個領域研究者的廣泛關注[13-17]。因此，本文對二維Logistic微分方程進行研究。

而近幾十年來，分數階（非整數）混沌系統迅速發展。但研究人員發現，對于一些分數階微積分總表現出階數小于3的混沌行為，如Hartley等[18]的研究闡述了該現象。分數階微分系統適合刻畫描述具有記憶、遺傳等特性的過程，區別于整數階微分系統，也是研究分數階微分系統的必要因素。整數階系統是分數階系統階次取整數時的特例，因此采用分數階混沌系統對混沌現象進行描述更具有普適性。此外大量研究表明，當混沌系統的階數為分數時仍表現出混沌現象，并且更能反映系統的工程物理現象。故本文將二維Logistic微分方程推廣到分數階領域，并引進了一種離散化方法對其進行離散求解，該離散化過程對分數階求解提供了理論指導，為分數階微積分的應用開拓了新領域。接下來，根據動力系統不動點穩定性定理和混沌動力學分析研究二維Logistic分數階微分方程的動力學性質以及混沌現象。

1 二維Logistic分數階混沌系統

1.1 混沌的定義

設（X，ρ）是一緊致的度量空間，f：X→X是連續映射，稱f在X是混沌的，如果：1）f具有初值敏感依賴性;2）f在X上拓撲傳遞;3）f的周期點在X中稠密[13]。

由于非線性動力學系統的混沌具有不可預測性、不可分解性和具有規律行為等特性，非線性系統隨時間的演變將趨向于維數比原來相空間低的極限集合，即吸引子。隨著控制參數的變化，簡單吸引子發展為奇異吸引子，此時系統是混沌的。

1.2 混沌的刻畫

1.3 分數階微積分的定義

分數階微積分是傳統微分和積分以任意階整數的一般化，近幾年因分數階微積分在科學技術領域的廣泛應用，吸引到很多學者，他們利用數值仿真研究該類方程。因為Caputo型分數階微分[20]描述問題的初始條件與整數階微分方程是一致的，因此本文選用Caputo型分數階微分進行研究，首先闡述Caputo型分數階微積分的定義：

2 離散化過程

當分數階微分模型建立之后，便面臨著如何求解的問題。目前，對于分數階微分方程的求解主要采用兩種方法：頻域法[21]和時域法[22]。但近來研究發現，第二種更加有效，因第一種方法在檢測混沌現象時不總是可靠的。

通常分數階微分方程的解析解求解困難，于是不得不借助數值解的方法并輔助計算機仿真。分數階微分方程數值解的方法主要包括：有限元方法、變分迭代法、Adomain分解法、預估校正法等。其中在文獻[23]分別對分數階Logistic模型和分數階Henon模型給出了分數階的數值求解方法，但該方法與預估校正法類似，求解結果比其他算法相比較為精確，但是兩者計算結果都比較復雜，并且前者的數值解不僅與當前狀態相關而且依賴過去所有狀態，故在進行數值仿真時加大了實驗難度，進而較難分析模型的動力學現象。

而近年來，具有時滯和分段常數變量的微分方程受到越來越多生態數學學者的關注，這一模型正解的穩定性、有界性、吸引性以及振動性得到了較全面的研究[24-26]。本文參考文獻[27-29]的離散化過程，定義了具有分段常數變元的二維Logistic分數階微分方程，并對其進行離散化處理。方程表達如下：

3 二維Logistic系統中的混沌

3.2 不動點的穩定性判別

根據3.1節給出的不動點的穩定性判定條件，此時將不動點f1fixed=（0，0）代入式（10），可得|K|max=1+4Wρ+Wγ，進而得出K+>1、K->1。可知不動點1為不穩定節點，此時不動點1是不穩定的。將不動點f2fixed=（（4ρ+γ）/（4ρ），（4ρ+γ）/（4ρ））代入式（10）可以推得，當0<γ<（2-4Wρ）/（3W）時，|K+|<1，|K-|<1，此時不動點2為穩定節點;當（2-4Wρ）/（3W）<γ<（2-4Wρ）/W時，|K+|<1，|K-|>1，此時不動點2為鞍點;而當γ>（2-4Wρ）/W，|K+|>1，|K-|>1，此不動點2為不穩定節點。此外將不動點2代入式（13）可知，當γ<1/（2W）-2ρ時，系統發生第一次分岔的分岔點為γ=（2-4Wρ）/（3W）或γ=（2-4Wρ）/W。本文將參數取值設定為ρ=2、α=0.95時，可計算得出γ=（2-4Wρ）/（3W）=0.34719和γ=（2-4Wρ）/W=1.04159，見圖1（a），該點為系統的分岔點。

3.3 通向混沌的道路

在動力系統中當控制參數變化到某個臨界值時，非線性系統的動力學性態發生定性變化的現象被稱為分岔，它是非線性系統內部固有的一種特性[32]。1981年，Eckmann[33]曾對各種可能的分岔現象進行了研究，歸納出走向混沌的三種途徑：1） Feigenbaum途徑（通過倍周期分岔）;2） Ruelle-Takens-Newhouse途徑（通過Hopf分岔）;3） Pomeau-Manneville途徑（通過陣法混沌）。

4 數值仿真與分析

為了在控制參數空間對系統的行為進行較全面的考察，這里有選擇地研究了控制參數沿該空間中軌線變化時系統行為的演化，且具代表性。

本章主要借助Matlab進行數值仿真來說明理論結果以及揭示系統式（8）復雜的動力學現象。這里主要采用控制變量法，即在其余參量保持正常值的條件下單獨探討一個參量對系統的影響[34]。本文探討了系統參數γ、階數α對分數階微分的影響。此外，一個系統發生混沌與否，一個關鍵的參考依據就是最大Lyapunov指數（Le）。故最大Lyapunov指數是對混沌最好的觀測者，當系統發生混沌時，最大Lyapunov指數為正，反之為負。

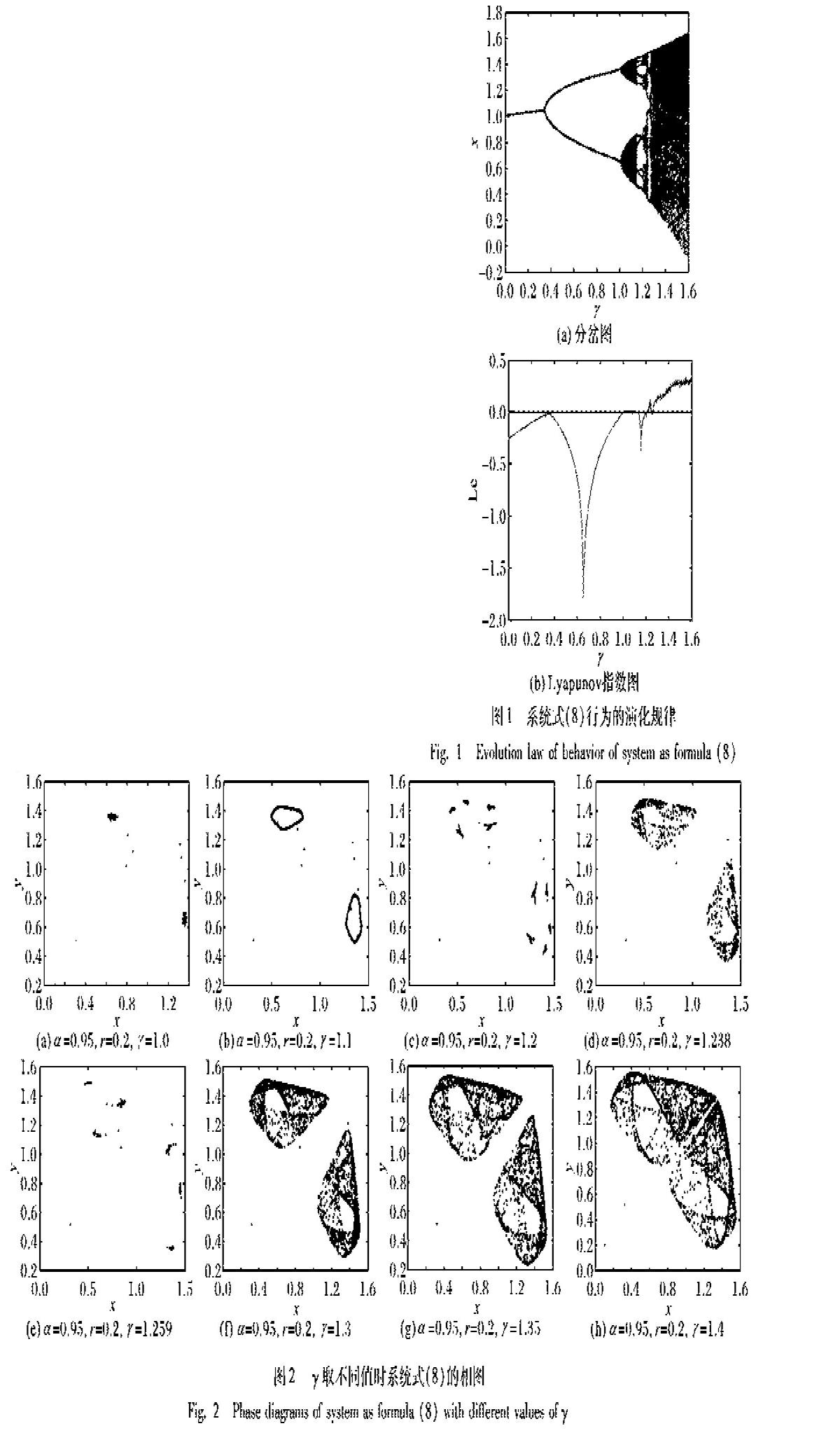
圖1為參數ρ1=ρ2=ρ=2、γ∈（0，1.6）時系統式（8）行為的演化規律，一般設定α=0.95，初值這里取（x0，y0）=（0.1，0.2），迭代次數為300，步長為0.002。可知當γ=0.25時系統趨于相平面的一穩定不動點（圖1（a））所示;當γ=1.0時，相平面出現兩個穩定的不動點（圖2（a））;當γ增加至1.1時，兩個穩定的不動點失穩，新的穩定狀態是圍繞著原有不動點的兩個極限環（圖2（b）），這個過程稱為Hopf分岔;當γ=1.2時，系統出現周期五窗口（圖2（c））;當γ增加至1.238時，相平面出現是奇怪吸引子（圖2（d）），可知此時最大Lyapunov指數L1>0（圖1（b）），系統的行為是混亂的;但隨著γ增加至1.259時，李雅普諾夫指數L1<0（圖1（b）），系統又回到了周期狀態，出現周期3窗口（圖2（e）），此時一般二維Logistic是按周期行為與混沌現象交替出現的間歇突發通向混沌的;γ繼續增加，軌道上的點按復雜方式扭曲，當γ=1.3，由圖1（b）可知此時L1>0，相平面出現的是奇怪吸引子，系統的行為是混沌的，并且隨著γ的增加，奇怪吸引子尺寸變大且靠近的程度縮小，彼此靠近（圖2（g）～圖2（h））。故可知，該演化行為是按周期行為與混沌現象交替出現的間歇通向混沌的，屬于Pomeau-Manneville途徑的典型代表，且該間歇與Hopf分岔有關。

接下來改變階數α，分數階階次α取定為0.80到0.95，此時分數階階次具有一般性，初值為（x0，y0）=（0.1，0.2），迭代次數為300，步長為0.002，如圖3所示。此時以參數α為控制變量，觀察在此區間內系統隨著參數改變的動力學現象。從圖3可知，隨著分數階階數α減小，分岔提前，穩定區域變小。

從圖3可以看出，分數階階次的改變影響著系統式（8）的運動狀態，故選定α為控制變量，變量區間為（0.8，1.3），步長為0.001，迭代次數為300，初值選定為x0=0.1，y0=0.2，不失一般性，這里分別選定γ=1.1和γ=1.35做出分岔圖如圖4所示。從圖4可以看出，隨著階數α的增加，系統逐漸趨于穩定。

此外混沌動力系統最重要的特性之一是對初值變化十分敏感，這意味著對當前軌跡的任意小的擾動都可能被放大，并在多次迭代之后導致顯著不同的未來行為。從（o（x1，y1），o′（x1′，y1′））不同的兩個點出發，兩條路徑之間的距離用歐氏距離衡量，表達如下：

為了顯示混沌系統對初始條件的敏感性，圖5繪制兩個無限接近但不相同的初始點（o（0.1，0.2），o′（0.1001，0.2））之間的距離（用“*”型線表示）。

由圖5可以看出，對于混沌系統而言，盡管對初值擾動很小，但在幾次迭代后被放大。而由穩定系統生成的另一基準線（用“”表示），盡管兩條軌跡從兩個差異略大的點（o（0.1，0.2），o′（0.19，0.2））出發，但隨著迭代進行，兩條軌跡之間的距離趨于0，表現出明顯的初始敏感性，進而驗證了上述的結論。

5 結語

本文研究了二維Logistic分數階微分方程，并運用了一種離散化方法對其進行離散求解、并以α、γ為控制參數通過數值仿真，并通過分岔圖、Lyapunov指數、相圖、時序圖對其離散化的二階差分模型的動力學現象進行分析。此外，探究了二維Logistic分數階微分方程離散化模型不動點的性質，給出了在參數空間中二維Logistic差分模型發生第一次分岔的邊界方程，并指出系統是按Pomeau-Manneville途徑走向混沌的，其間歇性與Hopf分岔有關。最后注意到當α→1時，即歐拉離散過程。但是區別于歐拉法的是，本文成功對二維Logistic分數階微分方程進行離散[29]。

參考文獻 （References）

[1] TONG X J. Design of an image encryption scheme based on a multiple chaotic map [J]. Communications in Nonlinear Science and Numerical Simulation， 2013， 18（7）： 1725-1733.

[2] 陳志剛，梁滌青，鄧小鴻，等.Logistic混沌映射性能分析與改進[J].電子與信息學報，2016，38（6）：1547-1551.（CHEN Z G， LIANG D Q， DENG X H， et al. Performance analysis and improvement of Logistic chaotic mapping [J]. Journal of Electronics & Information Technology， 2016， 38（6）： 1547-1551.）

[3] LEE T F. Enhancing the security of password authenticated key agreement protocols based on chaotic maps [J]. Information Sciences， 2015， 290： 63-71.

[4] 劉泉，李佩玥，章明朝，等.基于可Markov分割混沌系統的圖像加密算法[J].電子與信息學報，2014，36（6）：1271-1277.（LIU Q， LI P Y， ZHANG M C， et al. Image encryption algorithm based on chaos system having Markov portion [J]. Journal of Electronics & Information Technology， 2014， 36（6）： 1271-1277.）

[5] MAY R M. Simple mathematical models with very complicated dynamics [J]. Nature， 1976， 261（5560）： 459-467.

[6] FEIGENBAUM M J. Quantitative universality for a class of nonlinear transformations [J]. Journal of Statistical Physics， 1978， 19（1）： 25-52.

[7] RANI M， KUMAR V. A new experiment with the logistic function [J]. Journal of the Indian Academy of Mathematics， 2005， 27（12）： 143-156.

[8] VZQUEZ-MEDINA R， DAZ-MNDEZ A， del RO-CORREA J L， et al. Design of chaotic analog noise generators with logistic map and MOS QT circuits [J]. Chaos， Solitons & Fractals， 2009， 40（4）： 1779-1793.

[9] RANI M， AGARWAL R. A new experimental approach to study the stability of logistic map [J]. Chaos， Solitons & Fractals， 2009， 41（4）： 2062-2066.

[10] SAKAGUCHI H， TOMITA K. Bifurcations of the coupled logistic map [J]. Progress of Theoretical Physics， 1987， 78（2）： 305-315.

[11] WELSTEAD S T， CROMER T L. Coloring periodicities of two-dimensional mappings [J]. Computers & Graphics， 1989， 13（4）： 539-543.

[12] 王興元，王明軍.二維Logistic映射的混沌控制[J].物理學報，2008，57（2）：731-736.（WANG X Y， WANG M J. Chaos control of the coupled Logistic map [J]. Acta Physica Sinica， 2008， 57（2）： 731-736.）

[13] 張碩，蔡如華，陳光喜.結合二維混沌映射與小波變換的圖像加密方案[J].計算機工程與應用，2010，46（33）：191-194.（ZHANG S， CAI R H， CHEN G X. Image encryption algorithm on coupled chaotic map and wavelet transform [J]. Computer Engineering and Applications， 2010， 46（33）： 191-194.）

[14] 王興元，朱偉勇.二維Logistic映射中混沌與分形的研究[J].中國圖象圖形學報，1999，4A（4）：340-344.（WANG X Y， ZHU W Y. Researches on chaos and fractal of the coupled Logistic map [J]. Journal of Image and Graphics， 1999， 4A（4）： 340-344.）

[15] 王興元，梁慶永.復合Logistic映射中的逆分岔與分形[J].力學學報，2005，37（4）：522-528.（WANG X Y， LIANG Q Y. Reverse bifurcation and fractal of a compound Logistic map [J]. Chinese Journal of Theoretical and Applied Mechanics， 2005， 37（4）： 522-528.）

[16] 王興元，朱偉勇，顧樹生.一般二維二次映射中的混沌與分形[J].計算機輔助設計與圖形學學報，2000，12（6）：408-413.（WANG X Y， ZHU W Y， GU S S. Chaos and fractal of the general two-dimensional quadratic map [J]. Journal of Computer Aided Design and Computer Graphics， 2000， 12（6）： 408-413.）

[17] 朱偉勇，王興元.二維Logistic映射中的陣發混沌與分形[J].東北大學學報（自然科學版），1998，19（5）：509-512.（ZHU W Y， WANG X Y. Intermittent chaos and fractal of the coupled Logistic map [J]. Journal of Northeastern University （Natural Science）， 1998， 19（5）： 509-512.）

[18] HARTLEY T T， LORENZO C F， KILLORY QAMMER H. Chaos in a fractional order Chuas system [J]. IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications， 1995， 42（8）： 485-490.

[19] MICHAEL R B. Strange Attractors： Chaos， Complexity， and the Art of Family Therapy [M]. New York： John Wiley & Sons Inc， 1996： 3-76.

[20] 程金發.分數階差分方程理論[M].廈門：廈門大學出版社，2011：30-43.（CHENG J F. Theory of Fractional Differential Equations [M]. Xiamen： Xiamen University Press， 2011：30-43.）

[21] SUN H， ABDELWAHED A， ONARAL B. Linear approximation for transfer function with a pole of fractional-order [J]. IEEE Transactions on Automatic Control， 1984， 29（5）： 441-444.

[22] DIETHELM K， FORD N J， FREEd A D. A predictor-corrector approach for the numerical solution of fractional differential equations [J]. Nonlinear Dynamics， 2002， 29（1/2/3/4）： 3-22.

[23] SHUKLA M K， SHARMA B B. Stabilization of fractional order discrete chaotic systems [M]// AZAR A， VAIDYANATHAN S， OUANNAS A. Fractional Order Control and Synchronization of Chaotic Systems. Berlin： Springer， 2017： 431-445.

[24] 陳斯養，張艷.具有分段常數變量的捕食-被捕食模型的分支分析[J].蘭州大學學報（自然科學版），2012，48（3）：103-112，117.（CHEN S Y， ZHANG Y. Stability and bifurcation analysis of a predator-prey model with piecewise constant arguments [J]. Journal of Lanzhou University （Natural Sciences）， 2012， 48（3）： 103-112， 117.）

[25] 林詩仲，俞元洪.含分段常數變元的中立型時滯微分方程的振動定理[J].數學雜志，1997，17（1）：143-144.（LIN S Z， YU Y H. The oscillation theory of neutral delay differential equations with piecewise constant arguments [J]. Journal of Mathematics， 1997， 17（1）： 143-144.）

[26] 陳斯養，朱曉琳.具有時滯和分段常數變量的單種群收獲模型的分支分析[J].陜西師范大學學報（自然科學版），2013，41（2）：1-4.（CHEN S Y， ZHU X L. Bifurcation analysis of the single population harvest model with time-delay and piecewise constant variables [J]. Journal of Shaanxi Normal University （Natural Science Edition）， 2013， 41（2）： 1-4.）

[27] EL-RAHEEM Z F， SALMAN S M. On a discretization process of fractional-order Logistic differential equation [J]. Journal of the Egyptian Mathematical Society， 2014， 22（3）： 407-412.

[28] El-SAYED A M A， SALMAN S M. Chaos and bifurcation of the logistic discontinuous dynamical systems with piecewise constant arguments [J]. Malaya Journal of Matematik， 2013， 3（1）： 14-20.

[29] El-SAYED A M A， SALMAN S M. On a discretization process of fractional order riccati differential equation [J]. Journal of Fractional Calculus and Application， 2013， 4（2）： 251-259.作者核實

[30] El-SAYED A M A， SALMAN S M， ELABD N A. On a fractional-order delay Mackey-Glass equation [J]. Advances in Difference Equations， 2016， 2016： 137-1-137-11.https：//advancesindifferenceequations.springeropen.com/track/pdf/10.1186/s13662-016-0863-x

[31] 王興元，駱超.二維Logistic映射的動力學分析[J].軟件學報，2006，17（4）：729-739.（WANG X Y， LUO C. Dynamic analysis of the coupled Logistic map [J]. Journal of Software， 2006， 17（4）： 729-739.）

[32] 王興元.復雜非線性系統中的混沌[M].北京：電子工業出版社，2003：91-113.（WANG X Y. Chaos in Complex Nonlinear Systems [M]. Beijing： Publishing House of Electronics Industry， 2003： 91-113.）

[33] ECKMANN J-P. Roads to turbulence in dissipative dynamics system [J]. Review Modern Physics， 1981， 53（4）： 643-654.

[34] 古元風，肖劍.Willis環腦動脈瘤系統的混沌分析及隨機相位控制[J].物理學報，2004，63（16）：51-58.（GU Y F， XIAO J. Analysis of the Willis chaotic system and the control of random phase [J]. Acta Physical Sinica， 2004， 63（16）： 51-58.）