基于容差關系的多粒度粗糙集中近似集動態更新方法

徐怡 肖鵬

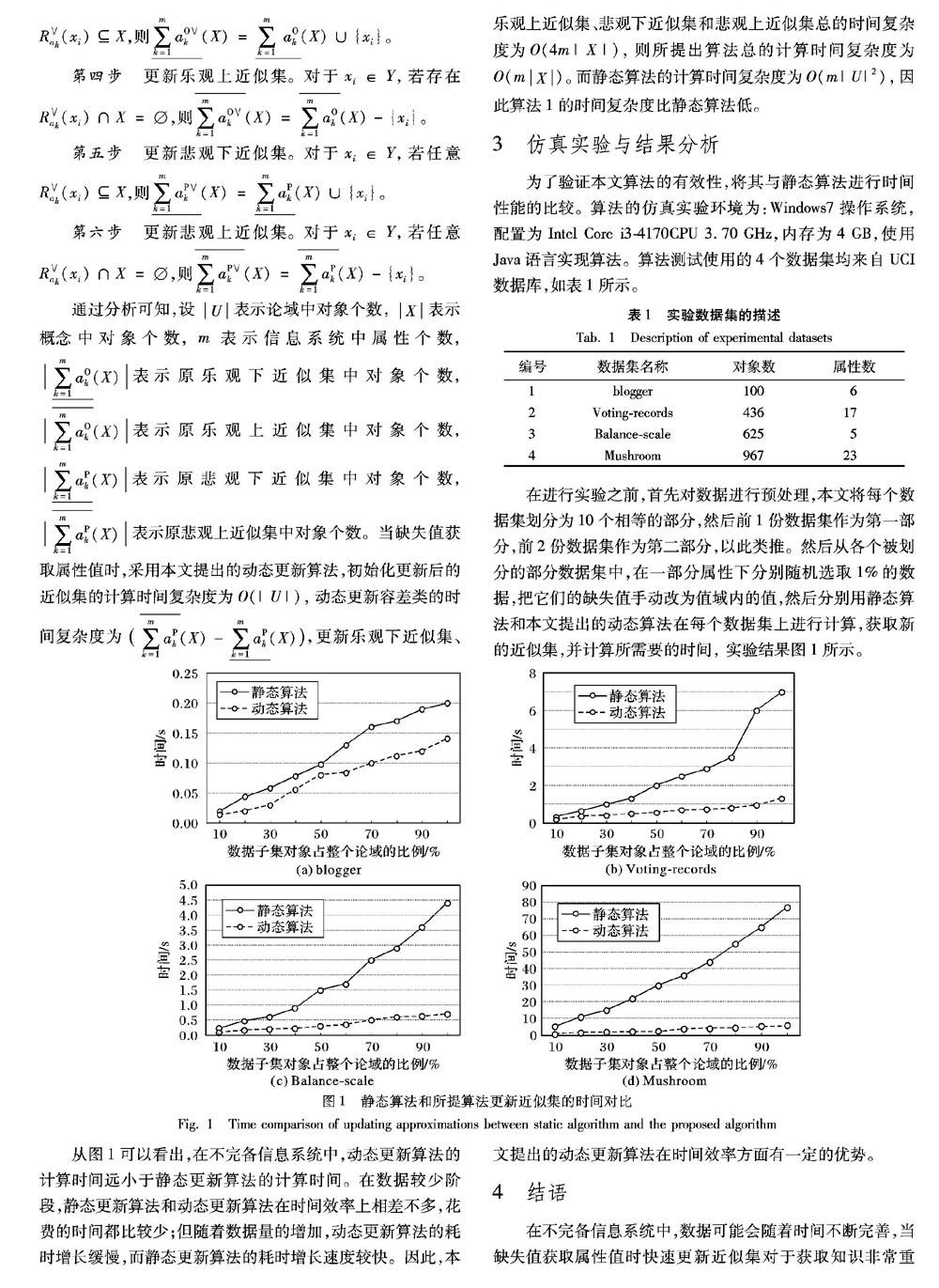
摘 要：針對不完備信息系統變化時缺失值獲取具體屬性值的特性，為解決多粒度粗糙集中更新近似集時間效率低的問題，提出了一種基于容差關系的近似集動態更新算法。首先，討論了基于容差關系的近似集變化的性質，并根據相關性質得出樂觀、悲觀多粒度粗糙集的近似集的變化趨勢; 然后，針對更新容差類效率低的問題，提出了動態更新容差類的定理;最后，在此基礎上，設計出基于容差關系的近似集動態更新算法。采用UCI數據庫中4個數據集進行仿真實驗，當數據集變大時，所提更新算法的計算時間遠小于靜態更新算法的計算時間，即所提動態更新算法的時間效率高于靜態算法，驗證了所提算法的正確性和高效性。

關鍵詞：不完備信息系統;多粒度;動態更新;容差關系多粒度粗糙集;近似集

中圖分類號：TP18

文獻標志碼：A

英文標題

Abstract： Focused on the issue that missing attribute values are obtained when an incomplete information system changes， in order to solve the problem of low time efficiency of updating the approximations in a multigranulation rough sets， a dynamic update algorithm based on tolerance relationship was proposed. Firstly， the properties of the approximations change based on tolerance relationship were discussed， and the change trends of the approximations of optimistic and pessimistic multigranulation rough sets were obtained according to the relevant properties. Then， a theorem of dynamic update tolerance class was proposed for the problem of low efficiency of updating tolerance class. Based on this， a dynamic update algorithm based on tolerance relationship was proposed. The simulation experiments were carried out using four data sets in UCI database. When the data set becomes larger， the calculation time of the proposed update algorithm is much smaller than that of the static update algorithm. The experimental results show that the time efficiency of the proposed dynamic update algorithm is higher than that of the static algorithm， which verifies the correctness and efficiency of the proposed algorithm.

英文關鍵詞Key words： incomplete information system; multigranulation; dynamic update; tolerance relationship multigranulation rough sets; approximations

0 引言

波蘭數學家Pawlak于1982年提出了一種能夠處理不精確數據的方法，即粗糙集理論[1]。在保持分類能力不變的前提下，這種理論方法將知識視為一種分類的能力，通過知識約簡導出決策規則。目前，粗糙集理論已在醫療診斷、模式識別、專家系統、預測分析以及機器學習等方面取得了巨大的成功[2-6]。

在現實生活中，數據的規模正在以前所未有的速度增長，數據可能隨時間變化而不斷變化，這可能會導致粗糙集中近似集的動態變化。當處理動態變化的數據時，傳統方法需要重新計算近似集，導致近似集更新時間增加。為了提高數據動態變化下近似集更新的時間效率，有必要設計一種近似集動態更新方法。這種動態更新方法是利用之前的計算結果來更新近似集，已被用于多種信息系統中的知識獲取。粗糙集背景下，學者們在論域變化、屬性集變化和屬性值域變化三個方面對知識的動態更新進行了大量研究。通過論域變化來更新知識方面：考慮到在集值有序信息系統中動態獲取知識的問題，Luo等[7]分析了計算近似集的更新機制，并提出了更新析取集值系統、合取集值系統中近似集增量算法;Zhang等[8]提出了鄰域粗糙集模型，并且利用矩陣的計算優勢設計出基于矩陣的近似集更新方法;Liu等[9]針對動態系統定義了一個基于精度和平均值的重要概念，并根據所提概念設計出近似集更新方法。通過屬性集的變化來更新知識方面：Zhang等[10]探討了由關系矩陣推導的基本向量的概念，并在屬性集變化時提出了通過更新矩陣來更新近似集的增量算法。通過屬性值域的變化來更新知識方面：Chen等[11-13]定義了粗化和細化屬性值的概念，并且在完備信息系統和不完備有序決策系統中分別提出了更新近似集的方法。

目前，Pawlak提出的經典粗糙集及擴展粗糙集理論都是建立在單一的二元關系基礎之上的。粒計算理論中的多粒度是一個重要概念，表示多個不同的粒度角度。錢宇華等通過對決策進行分析，說明了多個決策者之間的關系是相互獨立的，并使用多個二元關系來對目標概念進行近似逼近。根據上述理論分析：Qian等[14]提出了多粒度粗糙集的概念。在多粒度環境下，學者們對多粒度粗糙集的近似集動態更新方法進行了一系列深入的研究：Yang等[15]針對粒度結構增加的情況，提出了一種快速更新多粒度粗糙集的近似集方法;Hu等[16]通過對增加或刪除單個粒度的情況進行討論，設計出基于矩陣的多粒度粗糙集的近似集動態更新方法;胡成祥等[17]針對優勢關系多粒度粗糙集中屬性集的變化，定義了近似集動態更新的性質與定理，并根據提出的定理給出了近似集增量方法;Ju等[18]在多粒度模糊粗糙集環境中，提出了粒度結構變化時動態更新近似集和屬性約簡的方法;Hu等[19]首先討論了粗化和細化屬性值的動態機制，之后根據對應的動態機制設計了動態更新近似集算法。

目前，大多數多粒度粗糙集理論都是在完備信息系統下進行研究的。在完備信息系統下，處理的信息是完備的，所有對象的屬性值都是已知的，但在現實生活中，由于數據的龐大，我們很難保證每個對象屬性值的完備性。這時，多粒度粗糙集已經不適合處理這種不完備信息系統（Incomplete Information System， IIS）， 因此，Qian等[20]設計了不完備多粒度粗糙集模型，該模型采用一族容差關系來對目標概念進行近似逼近，因而適用于處理具有缺失值的不完備信息系統。然而，關于不完備多粒度粗糙集的研究主要集中在理論框架上，卻很少有學者來研究這些模型的近似集動態更新方法。隨著信息技術的飛速發展，數據的及時性具有重要意義， 因此，為了提高知識獲取的效率，缺失值獲取對應的屬性值時，近似集動態更新方法至關重要。本文著重研究了缺失值獲取屬性值時容差類動態更新的方法，并給出了缺失值獲取屬性值時，容差關系多粒度粗糙集中近似集動態更新算法。在UCI數據集中進行的仿真實驗表明，本文提出的近似集動態更新算法在缺失值獲取屬性值時是有效的，并且提高了時間效率。

4 結語

在不完備信息系統中，數據可能會隨著時間不斷完善，當缺失值獲取屬性值時快速更新近似集對于獲取知識非常重要。為了提高更新近似集的時間效率，本文在容差關系多粒度粗糙集模型中討論了缺失值獲取屬性值時動態更新近似集的相關過程，并提出對應的近似集動態更新算法。最后通過實驗驗證了本文算法在時間效率上優于靜態算法。在未來工作中，將拓展本文算法，并應用到其他類型的不完備信息系統當中。

參考文獻 （References）

[1] ??? PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences， 1995， 38（11）：88-95.

[2] ??? 梁吉業.信息系統中的不確定性與知識獲取[M].北京：科學出版社，2005：13-113.（LIANG J Y.Uncertainty and Knowledge Acquisition in Information Systems[M]. Beijing： Science Press，2005： 13-113.）

[3] ??? 王國胤. Rough集理論與知識獲取[M].西安：西安交通大學出版社， 2001：99-134.（WANG G Y.Rough Set Theory and Knowledge Acquisition[M].Xian：Xian Jiaotong University Press，2001：99-134.）

[4] ??? 張文修. 信息系統與知識發現[M].北京：科學出版社， 2003：15-25.（ZHANG W X.Information System and Knowledge Discovery[M].Beijing： Science Press， 2003：15-25.）

[5] ??? 李元誠， 方廷健. 基于粗糙集理論的支撐向量機預測方法研究[J]. 數據采集與處理， 2003， 18（2）：199-203.（LI Y C， FANG T J. Study of forecasting algorithm for support vector machines based on rough sets[J]. Journal of Data Acquisition & Processing，2003，18（2）199-203.）

[6] ??? FAKIH S J， DAS T K. LEAD： a methodology for learning efficient approaches to medical diagnosis[J]. IEEE Transactions on Information Technology in Biomedicine， 2006， 10（2）： 220-228.

[7] ??? LUO C， LI T， CHEN H， et al. Incremental approaches for updating approximations in setvalued ordered information systems[J]. KnowledgeBased Systems， 2013， 50： 218-233.

[8] ??? ZHANG J， LI T， DA R， et al. Neighborhood rough sets for dynamic data mining[J]. Information Sciences， 2014， 257（4）：81-100.

[9] ??? LIU D， LI T， DA R， et al. An incremental approach for inducing knowledge from dynamic information systems[J]. Fundamenta Informaticae， 2009， 94（2）： 245-260.

[10] ?? ZHANG J， LI T， DA R， et al. Rough sets based matrix approaches with dynamic attribute variation in setvalued information systems[J]. International Journal of Approximate Reasoning， 2012， 53（4）：620-635.

[11] ?? CHEN H， LI T， QIAO S， et al. A rough set based dynamic maintenance approach for approximations in coarsening and refining attribute values[J]. International Journal of Intelligent Systems， 2010， 25（10）：1005-1026.

[12] ?? CHEN H， LI T， DA R. Maintenance of approximations in incomplete ordered decision systems while attribute values coarsening or refining[J]. KnowledgeBased Systems， 2012， 31（7）：140-161.

[13] ?? CHEN H， LI T， RUAN D. Dynamic maintenance of approximations under a roughset based variable precision limited tolerance relation[J]. Journal of MultipleValued Logic and Soft Computing， 2012， 18（5）： 577-598.

[14] ?? QIAN Y， LIANG J， YAO Y， et al. MGRS： a multigranulation rough set [J]. Information Sciences， 2010， 180（6）： 949-970.

[15] ?? YANG X， QI Y， YU H， et al. Updating multigranulation rough approximations with increasing of granular structures[J]. KnowledgeBased Systems， 2014， 64（1）：59-69.

[16] ?? HU C， LIU S， LIU G. Matrixbased approaches for dynamic updating approximations in multigranulation rough sets[J]. KnowledgeBased Systems， 2017， 122： 51-63.

[17] ?? 胡成祥， 趙國柱. 優勢關系多粒度粗糙集中近似集動態更新方法[J]. 中國科學技術大學學報， 2017（1）：40-47.（HU C X， ZHAO G Z. Multigranularity rough set approximation set dynamic update method[J]. Journal of University of Science and Technology of China， 2017（1）： 40-47.）

[18] ?? JU H， YANG X， SONG X， et al. Dynamic updating multigranulation fuzzy rough set： approximations and reducts[J]. International Journal of Machine Learning & Cybernetics， 2014， 5（6）：981-990.

[19] ?? HU C， LIU S， HUANG X. Dynamic updating approximations in multigranulation rough sets while refining or coarsening attribute values[J]. KnowledgeBased Systems， 2017， 130（15）： 62-73.

[20] ?? QIAN Y， LIANG J， DANG C. Incomplete multigranulation rough set[J]. IEEE Transactions on Systems， Man， and Cybernetics-Part A： Systems and Humans， 2010， 40（2）：420-431.

[21] ?? 許韋， 吳陳， 楊習貝. 基于容差關系的不完備可變精度多粒度粗糙集[J]. 計算機應用研究， 2013， 30（6）：1712-1715. （XU W，WU C，YANG X B. Incomplete variable precision multigranulation rough sets based on tolerance relation[J]. Application Research of Computers，2013，30（6）：1712-1715.）

[22] ?? YANG H L， GUO Z L. Multigranulation decisiontheoretic rough sets in incomplete information systems[J]. International Journal of Machine Learning & Cybernetics， 2015， 6（6）：1005-1018.