基于孿生神經網絡的時間序列相似性度量

姜逸凡 葉青

摘 要：在時間序列分類等數據挖掘工作中，不同數據集基于類別的相似性表現有明顯不同，因此一個合理有效的相似性度量對數據挖掘非常關鍵。傳統的歐氏距離、余弦距離和動態時間彎曲等方法僅針對數據自身進行相似度公式計算，忽略了不同數據集所包含的知識標注對于相似性度量的影響。為了解決這一問題，提出基于孿生神經網絡（SNN）的時間序列相似性度量學習方法。該方法從樣例標簽的監督信息中學習數據之間的鄰域關系，建立時間序列之間的高效距離度量。在UCR提供的時間序列數據集上進行的相似性度量和驗證性分類實驗的結果表明，與ED/DTW-1NN相比SNN在分類質量總體上有明顯的提升。雖然基于動態時間彎曲（DTW）的1近鄰（1NN）分類方法在部分數據上表現優于基于SNN的1NN分類方法，但在分類過程的相似度計算復雜度和速度上SNN優于DTW。可見所提方法能明顯提高分類數據集相似性的度量效率，在高維、復雜的時間序列的數據分類上有不錯的表現。

關鍵詞：時間序列;相似性度量;神經網絡;孿生神經網絡

中圖分類號：TP391

文獻標志碼：A

文章編號：1001-9081（2019）04-1041-05

Abstract： In data mining such as time series classification， the similarity performance based on category of different datasets are significantly different from each other. Therefore， a reasonable and effective similarity measure is crucial to data mining. The traditional methods such as Euclidean Distance （ED）， cosine distance and Dynamic Time Warping （DTW） only focus on the similarity formula of the data themselves， but ignore the influence of the knowledge annotation contained in different datasets on the similarity measure. To solve this problem， a learning method of time series similarity measure based on Siamese Neural Network （SNN） was proposed. In the method， the neighborhood relationship between the data was learnt from the supervision information of sample tags， and ?an efficient distance measure between time series was established. The similarity measurement and confirmatory classification experiments were performed on UCR-provided time series datasets. Experimental results show that compared with ED/DTW-1NN（one Nearest Neighbors）， the overall classification quality of SNN is improved significantly. The Dynamic Time Warping （DTW）-based 1NN calssification method outperforms the SNN-based 1NN classification method on some data， but SNN outperforms DTW in complexity and speed of similarity calculation during the classification. The results show that the proposed method can significantly improve the measurement efficiency of the classification of dataset similarity， and has good performance for high-dimensional and complex time-series data classification.

Key words： time serie; similarity measure; neural network; Siamese Neural Network （SNN）

0?引言

時間序列是某一事件隨著時間的推移產生的一系列數據，由一定的時間間隔提取采集得到，對于時間序列的數據挖掘在工業、農業、經濟、醫療等領域時間序列都有廣泛的應用，例如證券市場的基金、股票數據分析研究[1]、輔助心電圖疾病診斷[2]等。時間序列的分類（Time Series Classification， TSC）等數據挖掘研究關鍵之一是時間序列之間的相似性度量，不同的相似性度量方法對時間序列的挖掘性能有很大的影響。目前主流的時間序列相似性度量使用L-P范數距離（如歐氏距離（European Distance， ED））和動態時間彎曲（Dynamic Time Warping， DTW）[3-6]。這兩種距離度量方法都局限于時間序列之間特征向量的固定公式數值計算，不能有效利用標注好的類別標簽。實際上，不同數據集的相似性描述并不能一概而論，數據樣本中包含的關于類別的先驗知識蘊含了相似性的統計規律，這些統計規律可以從標注好的訓練集中進行學習，進而構成更有效的數據相似性度量的表達方式。

近年來深度學習在很多領域得到了廣泛的應用，一些學者結合距離度量學習[7]與孿生神經網絡（Siamese Neural Network， SNN）進行了各種應用研究。SNN最早用于手寫簽名驗證[8]，驗證平板電腦上書寫的簽名真偽。文獻[9-11]將圖像識別中常用的卷積神經網絡組成孿生卷積網絡（Siamese Convolutional Neural Network， SCNN）模型應用于人臉識別（Face Verification）和行人重識別（Person Re-Identification）達到了不錯的識別率。文獻[12]將SNN用于文本匹配，每個文本對象分別由子網絡單獨向量化，計算兩個向量的余弦相似度來衡量這兩段文本的相似程度。這些方法的共同目標是學習一個好的距離度量，以便同類數據對之間的距離縮小，而異類數據對之間的距離盡可能地擴大。不同于一般基于特征向量的分類問題，時間序列數據往往具有高維度、屬性之間先后次序不可變等特點。

針對歐氏距離（ED）和DTW相似性度量方法的不足，借鑒SNN在模式識別等領域的良好表現，提出一種基于SNN的時間序列相似性度量學習方法，從標簽信息和序列樣本中學習其數據之間相似性關系的知識并形成度量模型，時間序列的時間順序則在輸入變量的排序中體現，SNN網絡隱含層輸出每個時間序列新的矢量表示，計算新矢量之間的距離度量作為網絡的輸出，該輸出作為原時間序列之間的相似度S=SNN（Xi，Xj）。本文依據該相似度結合近鄰分類器（K-Nearest Neighbor， KNN）[13]對時間序列進行分類，驗證了該方法的優勢。

1?相關理論基礎

區別于ED、DTW依賴于輸入空間中有意義且可計算的距離度量，SNN模型將度量學習的思想與神經網絡的非線性表示嵌入結合起來，以監督的方式從數據中學習數據之間的相似度的特定表達，經過SNN子網絡映射到新的度量空間中。

1.1?SNN網絡一般結構

輸出層作為輸入向量映射輸出的特征向量，用于度量模塊計算兩個子網絡輸出之間的相似度EW。EW的定義見式（12）。

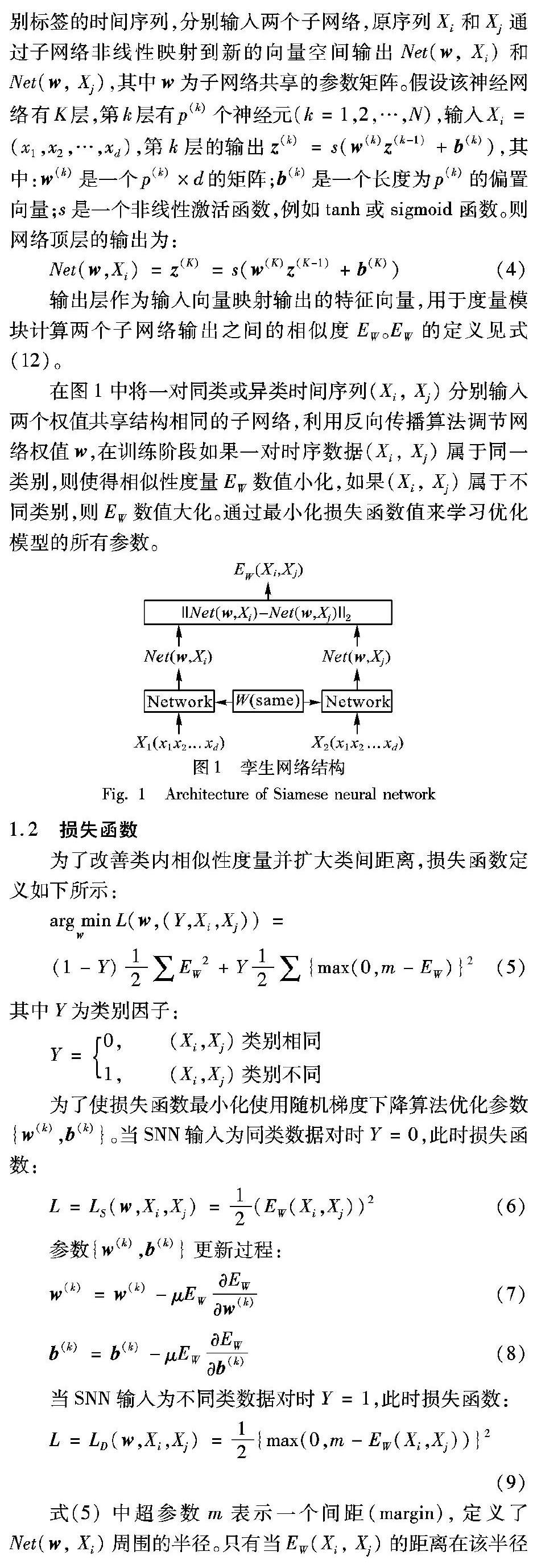
在圖1中將一對同類或異類時間序列（Xi， Xj）分別輸入兩個權值共享結構相同的子網絡，利用反向傳播算法調節網絡權值w，在訓練階段如果一對時序數據（Xi， Xj）屬于同一類別，則使得相似性度量EW數值小化，如果（Xi， Xj）屬于不同類別，則EW數值大化。通過最小化損失函數值來學習優化模型的所有參數。

1.3?度量函數

2?相似性度量實驗及分析

圖2分別展示了Beef數據集中5類時序數據的其中一個樣本。該數據集包含5個類別共60條數據，劃分訓練集和測試集各30條，每個類別有6條時間序列數據。為了更直觀地了解SNN度量學習方法的優勢，在Beef測試集上應用基于t分布的隨機近鄰嵌入（t-distributed Stochastic Neighbor Embedding， t-SNE）算法[15]對SNN的中間層嵌入輸出Net（w， Xi）進行了分析。

圖3中不同的數字代表相應的序列類別。t-SNE可視化表明SNN能夠很好地將相似的序列聚集在一起。為了比較，還使用相同數據原始序列的t-SNE圖。觀察圖2可以發現類別為第2類、第3類、第4類和第5類的時間序列樣本在形態變化上非常相似，反映在圖3（a）中相應的類別數據點之間相互混淆，不同類別序列的區分度不明顯。觀察圖3（b），通過學習有監督的成對約束信息，原序列經過子網絡映射到新的向量空間后，得到了一個能更有效地表達序列數據間鄰域關系的向量表示。這兩幅圖反映了SNN的潛在優勢：SNN在衡量時間序列樣本相似度時能更好地描述序列間相似度。

3?分類驗證實驗及比較

3.1?分類實驗流程

3.2?超參數選擇

本文采用一層隱含層的前饋神經網絡構建SNN模型子網絡。為了選擇合適的網絡結構，從UCR數據集中隨機選取了兩個時序數據集進行數值實驗，通過分析實驗結果探討SNN模型結構參數對錯誤率的影響，實驗結果如圖4所示。實驗中模型權值參數通過在區間[-0.05，0.05]內的均勻分布采樣來初始化，選擇Adam優化算法[16]訓練模型，多次實驗后選擇使用sigmoid函數作為神經元激活函數，實驗程序基于Python和Tensorflow平臺。

采用錯誤率作為分類質量的評價標準，并對比以ED、DTW作為相似性度量的分類錯誤率。圖4展示了隨著神經元數量增加時錯誤率的變化。

錯誤率的定義：分類錯誤的樣本數占樣本總數的比例。

在相同參數下進行五次實驗取平均值為實驗結果。圖4的實驗結果顯示，隨著隱層神經元個數的增加分類錯誤率隨之明顯下降，較多的神經元有利于學習數據的特征表示，但存在一定的飽和性。

3.3?數值實驗

將SNN模型結合1-NN分類器與主流的ED/DTW-1NN分類器相比較，部分實驗結果引用自文獻[17]。在UCR公共數據集上選取22個數據集完成對比實驗，數據在獲取時已劃分好訓練集與測試集，所有錯誤率都在測試集上計算。表1展示了所對比的三種相似度度量方法在22個公共數據集上的分類錯誤率，加粗的數值表示所有對比方法中最優的結果。其中SNN-1NN的結果是五次實驗平均值。

從表1展示的實驗結果來看，總體上分類錯誤率ED-1NN>DTW-1NN>SNN-1NN，三種分類器在22個數據集上的平均分類錯誤率分別是0.251、0.236、0.191， SNN-1NN具有明顯的優勢，其分類錯誤率在其中12個數據集上顯著低于主流的DTW-1NN分類器，相對于ED-1NN在其中19個數據集上表現明顯占優，在其余數據集上分類錯誤率相近。若對于不同數據集測試選擇更合適的調整網絡結構則可進一步降低SNN-1NN的分類錯誤率。

4?結語

本文針對目前時間序列相似性度量方法的優點和不足，借鑒度量學習和神經網絡模型相結合的思想，提出了一種基于SNN模型的度量學習方法，可提高對時間序列數據挖掘的性能。將該方法結合最近鄰算法在UCR公共數據集上進行分類實驗，結果表明，與ED/DTW-1NN相比在分類質量總體上有明顯的提升。基于DTW-1NN的模型在部分數據上表現仍然優于SNN-1NN分類方法，但在分類過程的相似度計算復雜度和速度上，SNN優于DTW。在之后的工作中，可對本文方法作進一步的研究，針對數據集特點探討更加合理的網絡結構，改進模型的學習算法擴展到時間序列數據挖掘聚類等任務中的應用。

參考文獻（References）

[1] 崔婧， 趙秀娟， 宋吟秋.中日股價序列相似性的比較分析[J]. 系統工程理論與實踐， 2009， 29（12）： 125-133. （CUI J， ZHAO X J， SONG Y Q. Similarity analysis on China's and Japan's security price series[J]. Systems Engineering — Theory and Practice， 2009， 29（12）： 125-133.）

[2] SIVARAKS H， RATANAMAHATANA C A. Robust and accurate anomaly detection in ECG artifacts using time series motif discovery[J]. Computational and Mathematical Methods in Medicine， 2015， 2015： 453214.

[3] 陳海燕， 劉晨暉， 孫博.時間序列數據挖掘的相似性度量綜述[J]. 控制與決策， 2017， 32（1）： 1-11. （CHEN H Y， LIU C H， SUN B. Survey on similarity measurement of time series data mining[J]. Control and Decision， 2017， 32（1）： 1-11.）

[4] BERNDT D J， CLIFFORD J. Using dynamic time warping to find patterns in time series[C]// AAAIWS 1994： Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining. Menlo Park， CA： AAAI Press， 1994， 10（16）： 359-370.

[5] FALOUTSOS C， RANGANATHAN M， MANOLOPOULOS Y. Fast subsequence matching in time-series databases[C]// SIGMOD 1994： Proceedings of the 1994 ACM SIGMOD International Conference on Management of Data. New York： ACM， 1994： 419-429.

[6] 李海林， 梁葉， 王少春.時間序列數據挖掘中的動態時間彎曲研究綜述[J]. 控制與決策， 2018， 33（8）： 1345-1353. （LI H L， LIANG Y， WANG S C. Review on dynamic time warping in time series data mining[J]. Control and Decision， 2018， 33（8）： 1345-1353.）

[7] 沈媛媛， 嚴嚴， 王菡子.有監督的距離度量學習算法研究進展[J]. 自動化學報， 2014， 40（12）： 2673-2686. （SHEN Y Y， YAN Y， WANG H Z. Recent advances on supervised distance metric learning algorithms[J]. Acta Automatica Sinica， 2014， 40（12）： 2673-2686.）

[8] BROMLEY J， GUYON I， LECUN Y， et al. Signature verification using a “siamese” time delay neural network[C]// NIPS 1993： Proceedings of the 6th International Conference on Neural Information Processing Systems. San Francisco， CA： Morgan Kaufmann Publishers， 1994： 737-744.

[9] CHOPRA S， HADSELL R， LECUN Y. Learning a similarity metric discriminatively， with application to face verification[C]// CVPR 2005： Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. ??Washington， DC： IEEE Computer Society， 2005： 539-546.

[10] WANG F Q， ZUO W M， LIN L， et al. Joint learning of single-image and cross-image representations for person re-identification[C]// CVPR 2016： Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. ?Washington， DC： IEEE Computer Society， 2016： 1288-1296.

[11] DONG Y， ZHEN L， SHENG L， et al. Deep metric learning for person re-identification[C]// Proceedings of the 2014 22nd International Conference on Pattern Recognition. Piscataway， NJ： IEEE， 2014： 34-39.

[12] HUANG P S， HE X D， GAO J F， et al. Learning deep structured semantic models for Web search using clickthrough data[C]// Proceedings of the 22nd ACM International Conference on Conference on Information & Knowledge Management. New York： ACM， 2013： 2333-2338.

[13] COVER T， HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory， 1967， 13（1）： 21-27.

[14] BATISTA G E， WANG X， KEOGH E J. A complexity-invariant distance measure for time series[EB/OL]. [2018-05-10]. https：//epubs.siam.org/doi/pdf/10.1137/1.9781611972818.60.

[15] MAATEN L， HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research， 2008， 9： 2579-2605.

[16] KINGMA D P， BA J. Adam： a method for stochastic optimization[EB/OL]. [2018-05-10]. https：//arxiv.org/pdf/1412.6980.

[17] CHEN Y， KEOGH E， HU B， et al. The UCR time series classification archive [DB/OL]. [2018-05-10]. http：//www.cs.ucr.edu/～eamonn/time_series_data/.