模糊數學理論在地裂縫災害危險性評估中的應用
文新征 甄平福 彭 敏 拜亞南 羅曉峰
(1. 信息產業部電子綜合勘察研究院, 陜西 西安 710054;2. 中交第一公路勘察設計研究院有限公司, 陜西 西安 710075;3. 內蒙古科技大學,內蒙古 包頭 014010)
地裂縫是一種常見的區域性地質災害,在世界各國都有發現,特別是在許多經濟發達人口密集的大中型城市,其災害頻率及發展狀況逐年加劇,其中西安地裂縫已成為典型代表。在大西北建設戰略的背景下,加快西安城市發展步伐已成為迫切需要,然而地裂縫災害卻成為制約其發展的一個重要的“瓶頸”,因此開展地裂縫研究工作并對其災害危險性進行分析評估顯得尤為重要。
目前對地裂縫地質災害危險性評估的方法多為定性的方法,即主要在調查和收集資料的基礎上,通過分析成因、發展狀況及危害程度,綜合劃分危險性分區,評價其對建設工程的影響作用。這種評估方法往往帶有很大的主觀性,忽略了評估系統各因素之間內在關系規律的揭示,對在建設工程中應用的理論和實踐指導具有一定的局限性。因此,筆者以西安地裂縫為例嘗試從研究區評估系統出發,提出地裂縫災害危險性綜合評價指標體系及分級標準,運用模糊數學理論[1-3],構建量化模型,分析研究各評價指標對評估分級標準的影響關系,收到了較為有效的評估效果。
1 構建地裂縫災害評估指標體系及標準分級
根據研究區西安地裂縫構造特征和成因機制分析[4]及分布發展變化規律,參照相關已有研究資料[5-7],可以認識到,本質上西安地裂縫是先存地質構造(斷裂系) 在現代引張應力場作用下蠕動而產生的斷裂,表現為地面開裂、裂縫,這里的現代引張應力場作用主要是指地震活動、水文活動及人類工程活動等加劇斷裂活動的作用。為了便于評估指標的選取和評估系統的建立,分別從基本因素、影響因素及災害特征三大方面出發,綜合篩選了8 個指標建立西安地裂縫災害危險性評估指標體系及標準分級,詳見表1。
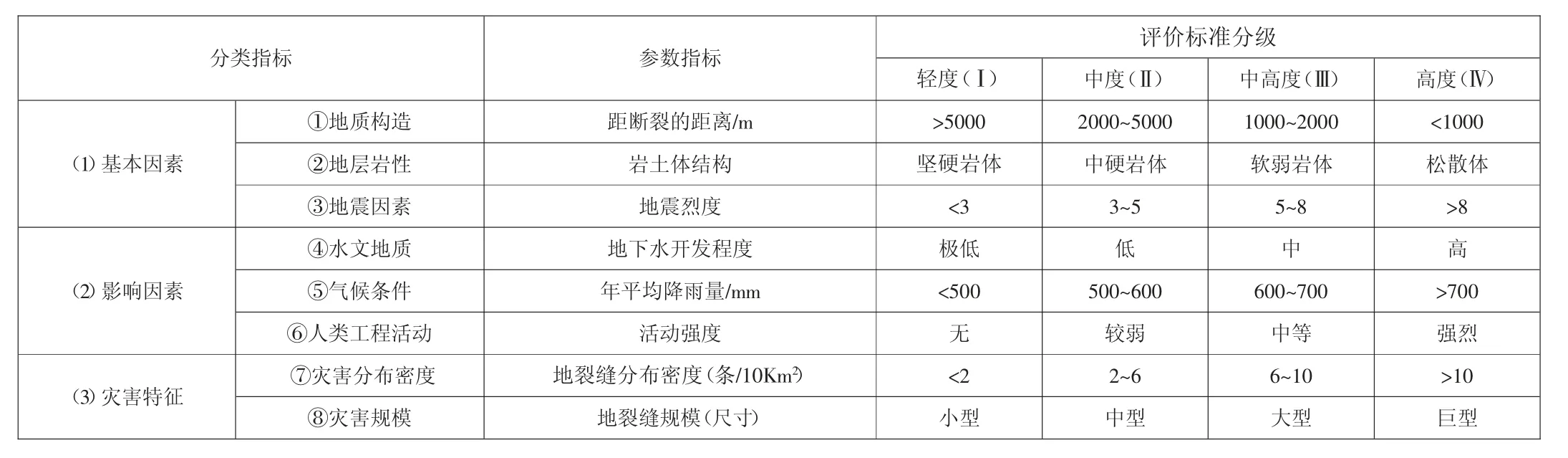
表1 地裂縫災害危險性評估指標體系及標準分級
2 模糊數學理論在地裂縫災害危險性評估系統中的應用
2.1 模糊數學理論概述
模糊數學是從量上來研究分析和解決模糊問題的一個數學分支,它是以1965 年美國控制論專家L.A.Zadeh 教授最早提出的“模糊集合論”[8]為基礎發展起來的數學理論。模糊數學的基本思想是以模糊系統為研究對象,通過“模糊集合”建造數學模型,逐步建立運算、變換規律,最終尋求解決模糊問題的有效數學方法。目前,模糊數學應用中的方法有模糊模式識別法、模糊聚類分析法、模糊綜合評判法及模糊數值計算法等。
工程建設中的地質災害問題常常錯綜復雜,蘊含著眾多的模糊不確定性,例如:地質概念難以精確定義,劃分界限模糊不清;地質系統本構關系復雜,難以識別;參數量測不夠精確等。因此,從一定意義上說,模糊性已經成為解決工程地質問題的首要矛盾。在此,為了有效解決地裂縫災害危險性評估的模糊性問題,筆者嘗試運用模糊綜合評判的方法進行相應的分析研究。
2.2 模糊綜合評判的方法及應用
模糊綜合評判就是運用模糊數學的方法對受多個因素制約的模糊系統(事物或對象) 進行總的評判。模糊綜合評判的數學模型依據評判系統因素分類層次可分為一級模型和多級模型,本文對地裂縫災害危害性評估包括一級模型模糊綜合評判及二級模型模糊綜合評判。
1) 一級模型模糊綜合評判
①建立評判模糊集合,建立評判指標因素集U={u1,u2,u3,u4,u5,u6,u7,u8},其中u1~u8分別依次對應上表1中①~⑧各指標;建立評判集V={v1, v2, v3, v4},其中v1~v4分別依次對應上表1 中Ⅰ~Ⅳ各評價標準分級;
②確定各評價因素的隸屬度, 評價因素隸屬度的確定方法:對于定性指標因素(如表1 中②、④、⑥、⑧),主要采用專家經驗評定法,直接給出隸屬度取值,見表2;對于定量指標因素(如表1 中①、③、⑤、⑦),常用隸屬函數代入實測值確定。隸屬函數的常見分布形式有矩型、梯型、拋物線型、正態分布、哥西分布及嶺型分布等,具體應用中根據研究對象分布特征選定。在地裂縫災害評估系統中,綜合各因素分布特征,選取“梯型分布”為隸屬度函數,其分布函數圖形見圖1。
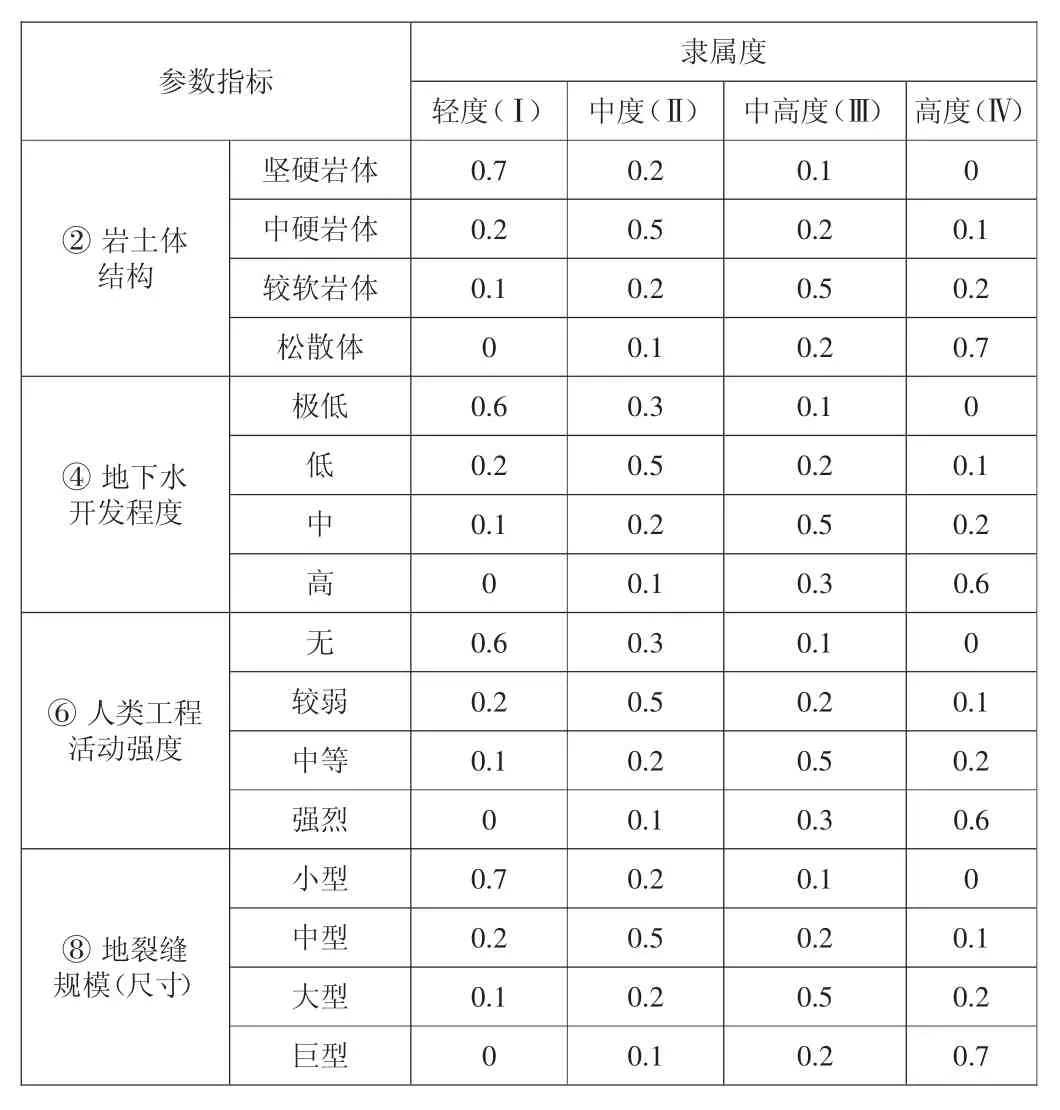
表2 定性指標隸屬度取值表

圖1 “梯型”隸屬度函數分布圖
圖1 中,A (x) 表示定量指標因素分別對應評價分級的隸屬度函數,x 為因素實測值;a、b、c 分別為各因素分級標準取值,a′、b′、c′為其相應的模糊性修正值,且a<a′<b<b′<c′<c。其具體表達公式如下:
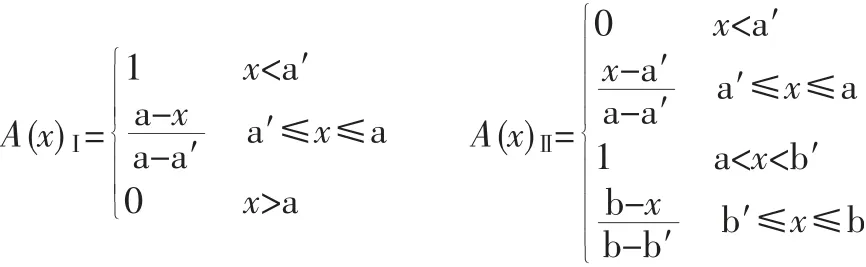
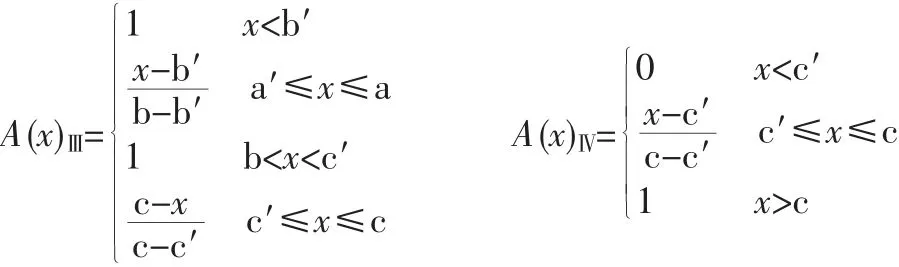
③確定單因素評判模糊矩陣,根據從U 到V 的隸屬度可得模糊矩陣R,即建立評判指標因素集到評判集的一個模糊映射關系。

可見,由(U,V,R) 就共同構成了一個評估系統模型。
④確定各評價因素的權重,在評判系統中,各評價因素對評價分級的影響作用及重要性各不相同,因此綜合評價時應賦予一定的權重值。可根據已有研究成果或結合專家經驗先估計出一組權重值,然后通過大量的試運算,比較分析運算得到的綜合評判結果與實際情況的擬合性,直到兩者基本一致為止。由此可得U 上的一個權重系數模糊子集A:

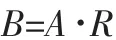
其中“·”表示模糊子集的合成運算,運算法則同普通實數矩陣的乘法運算過程相同,只需將實數加法中的“+”改為集合取大運算的“∨”,將實數乘法中的“·”改為集合取小運算的“∧”。即

2) 二級模型模糊綜合評判
二級模型可以進一步彌補一級模型的綜合評判的不足之處,主要表現為:當評價因子過多時,其權重取值就會偏小,往往導致評價結果差異性也會變小;另外,當評價因子過多時,會使對各因子的權重分配的合理性變得更加困難。根據表1 對評價指標的兩級分類情況,八個參數指標又可以劃分為三大類,依此進行二級模糊綜合評判的方法步驟如下:
①將因素集U 分為三個子集U1、U2、U3(分別對應表1中基本因素、影響因素、災害特征),且滿足U1∪U2∪U3=U,且兩兩取交集為空集。U1={a1, a2, a3} , U2={a4, a5, a6} , U3={a7, a8}。
②對每個子集Ui 分別按一級模型進行綜合評判:
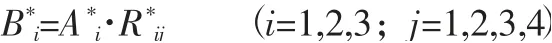
其中,A*i為Ui上的權重分配,且滿足Σa*i=1。
③將每個子集Ui 進行單因素評判,可得二次模型評判矩陣:

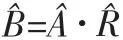
2.3 評定結果分析
3 結語
1) 通過對模糊數學理論在西安地裂縫災害危險性評估中的應用分析表明:以“模糊集”和“隸屬度”為基礎的模糊綜合評判模型,運用數學量化手段解決地質災害評估系統的模糊性問題,清晰明了,簡單可行,對于同類工程地質問題具有參考價值及指導意義;2) 在模糊綜合評判建模過程中,依然存在著不足之處。其一,評價系統中定性指標隸屬度的取值主要依據專家經驗評定的方法確定,具有一定的主觀色彩;其二,各評價因子權重分配采用先是估值再進行實效擬合性試算的方法,當系統復雜參數較多時,運算工作量將加大;其三,在采用多級綜合評價模型時,評價系統中參與因子越多,多層次分級分類越困難,同時也增加了評價因子隸屬度及權重分配的難度等。

