T-S模糊模型的FGD系統pH值建模研究

蔣靜江

（廣東省能源集團有限公司珠海發電廠，廣東 珠海519000）

1 引言

在日常生活中，有很多的時變系統，并且需要研究的對象比想象中復雜很多。現場實際因素的影響使得并不容易將應用理論和實驗應用在研究對象上，對此，最常用的方法就是建模。在數學領域建模并不能夠達到具體化，轉換為借助于一個系統以及處于過程中的相關變量之間的某種關系來反映實現的數學結構[1-2]。脫硫系統能夠正常運行，其中pH是最重要的控制參數之一，直接關系到脫硫效率和脫硫效果。針對珠海發電廠FGD系統的運行情況，其值在5.5～6.0是最佳范圍，整個控制目的在于保證pH穩定[3-4]。基于控制FGD系統pH值的非線性、多時變、強耦合的特點，用T-S模糊模型對特定值進行數學建模來進行分析及優化[5]。

2 模型概況

面對多維模糊推理中的推理規則龐大的問題，由Takagi和Sugeno提出了一種新的模糊推理模型，稱為Takagi-Sugeno（T-S）模糊模型。模型的輸入函數是規則后件：

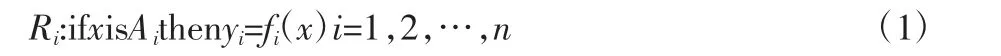
這種語言規則描述的模型展開第i條規則可寫為：

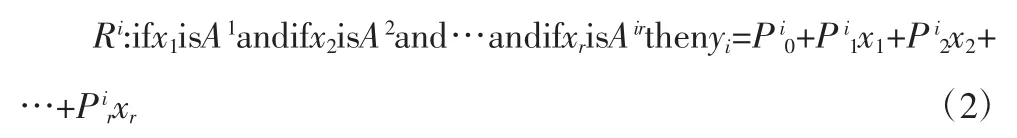
這里，Air在模糊系統中是第i條規則前件的模糊集合；Pim（m=1,2，……，k）是系統參數；x=[x1，x2，……，xr]是輸入變量；yi是輸出變量，輸入模糊，輸出確定，整個模糊推理過程的輸入與輸出的關系呈線性。

對輸入變量x來說，應用模糊規則來計算每個輸入變量的隸屬度：

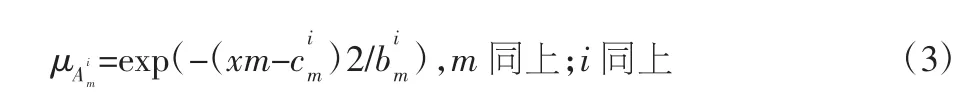
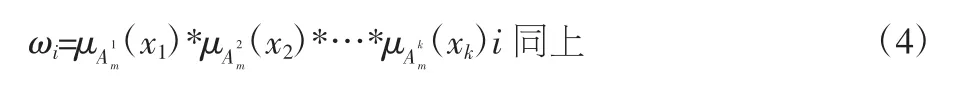
通過計算得到輸出值yi。

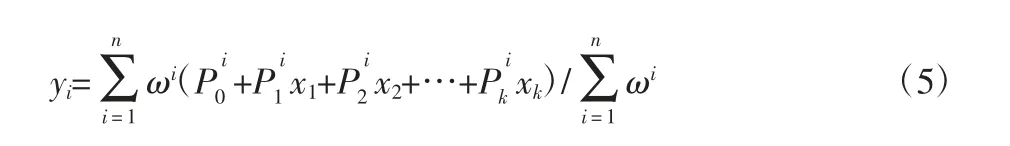
式中，k是輸入參數；n是子集數。

3 網絡辨識

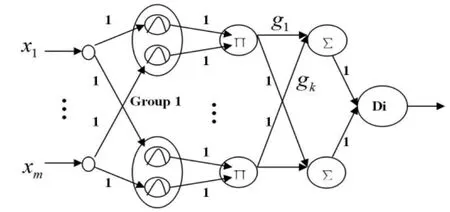
圖1 T-S模糊神經網絡結構

由圖1可以看出，T-S模糊神經網絡是由五層從左向右的網絡組成：前為輸入層，中間區域為輸出層、模糊化層和模糊條件層，后端為輸出層；與輸入層連接的是輸入向量x；模糊隸屬度值μ是模糊化層將隸屬度函數公式（3）對輸入值進行模糊化得到的。模糊連乘公式（4）用于模糊條件層，而輸出則是通過模糊決策層采用公式（5）計算得出。

學習算法如下：

①誤差的計算

這里，yd是期望輸出；yc是實際輸出；e是期望輸出和實際輸出的誤差。

②系數的修正

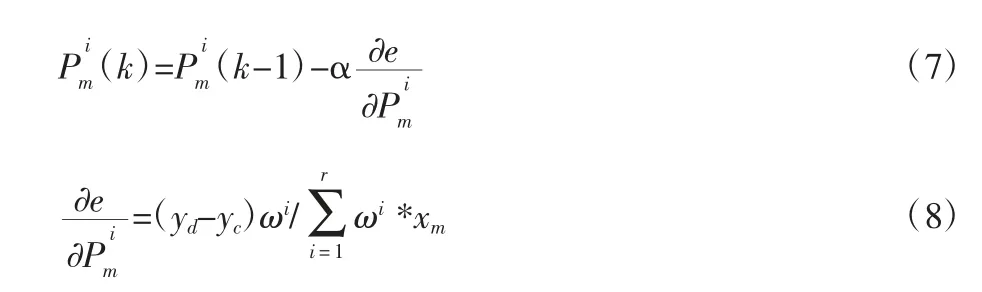
③參數的修正

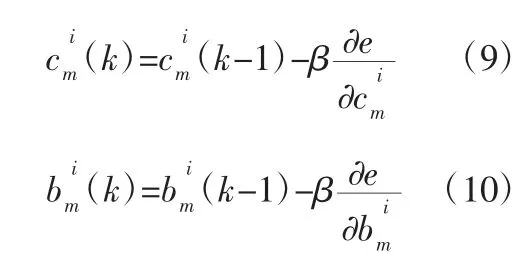
4 建模與仿真

負荷、石灰石供漿、石膏漿液脫水和脫硫效率等條件直接影響pH值。本次建模，是機組負荷在700MW、石膏漿液脫水沒有運行的情況下進行，對珠海發電廠#1機組FGD系統PH值每隔5min測取數據，最終的控制范圍為5.5～6.0，根據72個小時整3天測量的數據應用T-S模糊模型建立系統模型[6-7]。系統算法流程如圖2所示，實測數據曲線與模型預測曲線對比如圖3所示，可以清晰地看到實測值與預測值的對比關系。

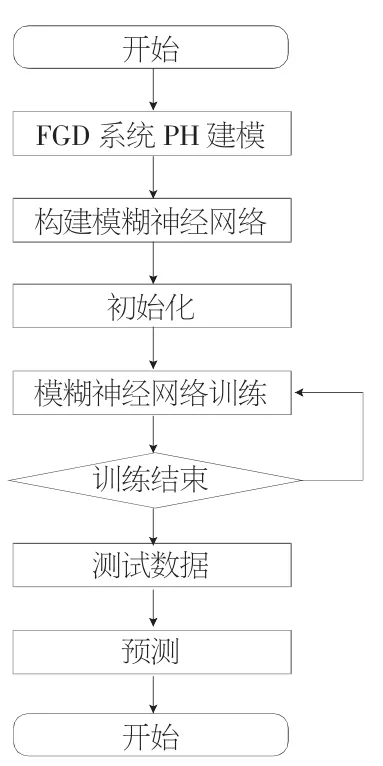
圖2 模糊神經網絡FGD系統PH建模算法流程圖

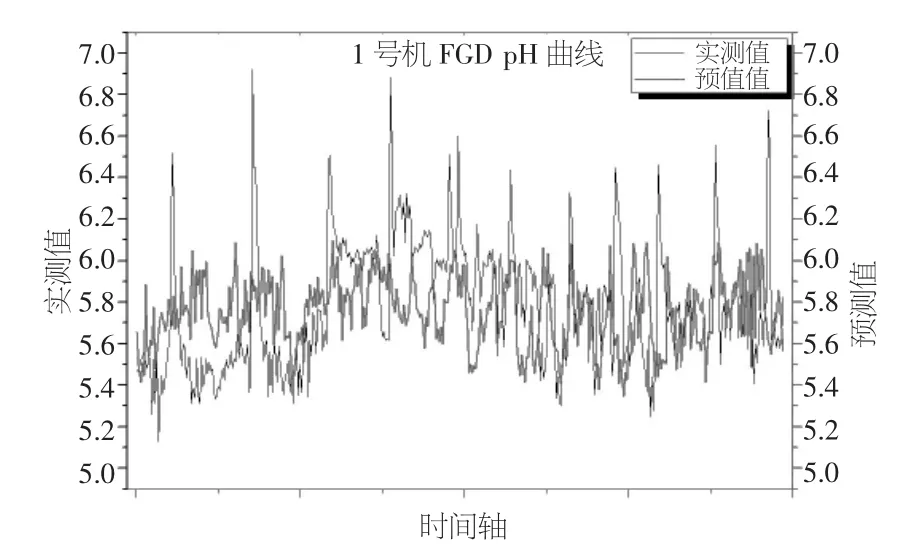
圖3 實測數據曲線與模型預測曲線對比圖

5 結論

本文是建立在T-S模糊神經網絡算法上，針對脫硫吸收塔pH值這一參數進行數學建模，采取現場樣本數據，進行實測曲線擬合，然后將其與預測模型輸出曲線對比，通過仿真實驗可見，預測曲線在相同負荷等情況下能夠將pH值穩定在目標值范圍內，表明本文中建立的數學模型，能夠與實際情況相吻合，且真實地反映了珠海發電廠1號機組在負荷700MW時脫硫吸收塔pH值情況，對以后分析研究和控制系統的優化有積極方面的作用，為機組達到更優工況和提高經濟效益也有很大幫助。