Topological magnon insulator with Dzyaloshinskii-Moriya interaction under the irradiation of light?
Liang Chen(陳亮)
School of Physics and Electronic Engineering,Taishan University,Taian 271000,China
Keywords: magnon,light,Brillouin-Wigner theory,Dzyaloshinskii-Moriya
1. Introduction
A topological insulator is a material that has a bulk band gap like an ordinary insulator but whose surface contains conducting states.[1,2]The search for topological states of quantum matter is one of the hottest topics in condensed matter physics. The topologically protected edge states is not unique to electronic systems. A growing number of studies investigate the possibility of topological properties on magnons in two-dimensional (2D) honeycomb systems[3-12]due to their similarity to electrons in graphene.[13,14]The ferromagnetic spins on a 2D honeycomb lattice can be topologically nontrivial when a proper nearest neighbor exchange exists.[3]In Ref. [4], the authors investigated the properties of magnon edge states in a ferromagnetic honeycomb spin lattice with a Dzyaloshinskii-Moriya interaction (DMI). Beginning from an isotropic Heisenberg model of localized spin moments in a honeycomb lattice,Fransson et al.[5]addressed the possibility of emerging Dirac magnons. Ferreiros[7]et al. studied the influence of lattice deformations on the magnon physics of a honeycomb ferromagnet when a DMI is considered.Owerre[8]showed that the magnon Hall effect is realizable in a twoband model on the honeycomb lattice,and studied the thermal Hall conductivity. Employing the Landau-Lifshitz-Gilbert phenomenology, bulk and edge spin transport in topological magnon insulators have been studied.[9]The spin Nernst effect of magnons in a honeycomb antiferromagnet in the presence of a DMI has been demonstrated.[10,11]
Another direction that the study of topological phases has taken in recent years is manipulating the topological and transport properties of quantum systems under the influence of a periodic drive.[15-17]Changes in the band structure from a nontopological band structure to a topological one can occur. In cold atom systems, periodic changes in the laser fields establish an optical lattice potential.[18,19]In solid state systems,periodically modulated quantum systems can be effectively described by a static Hamiltonian. Therefore, magnon systems deserve consideration. In this work, we study the magnon on a honeycomb lattice with a DMI under the irradiation of light.[20-24]We study the effects of the interplay between the DMI and light.
The rest of this paper is organized as follows. In Section 2,we present the tight-binding magnon model on the honeycomb lattice. Based on the Brillouin-Wigner theory,we obtain the effective tight-binding Hamiltonian with a circularly polarized light. In Section 3, the Berry curvature and Chern number of the system are presented. In Section 3, the corresponding low-energy Dirac model is studied. Our conclusions are given in Section 5.
2. Model
We consider a ferromagnetic model on a honeycomb lattice. The corresponding Hamiltonian is

where Si= (Sxi,Syi) is the spin moment at site i. J >0 is the nearest neighbor ferromagnetic exchange coupling. The second term is the DMI between the second nearest neighbors. The constants νij=di×dj/|di|/|dj|with the vectors diconnecting site i to its second nearest neighbor j is shown in Fig.1.

Fig.1. The honeycomb lattice structure,with the nearest neighbor and the second nearest neighbors labeled by ai and di,respectively.
Using Holstein-Primakoff transformation S+i=Sxi+Syi =and Szi=S-niwith ni=c?i ci,we obtain

where ciand c?i are magnon operators,and i,j=A,B label the two sublattices of the honeycomb lattice denoted by different colors in Fig.1. The Hamiltonian in the momentum space can be written as H=whereand

where

3, d1,3=2, and d3,6= ±(1,0). We have set the lattice constant as 1 throughout the paper. In the absence of DMI, the magnon bands are massless at the two Dirac points K=(4π/3,0)and K′=(-4π/3,0).
Next, we consider the effect of the circularly polarized light represented by the time-dependent vector potential

where A = E0/ω, and E0and ω are the field strength and frequency, respectively. Then, the response of the lightilluminated system can be obtained by substituting k with k+eA(t). Based on the Brillouin-Wigner theory,[25,26]we can write the effective Hamiltonian as


where ~H0is equal to the bare Hamiltonian in the absence of light H(k)in Eq.(3)except for the constant term with renormalization of the parameters: J =JJ0(~A) and D=DJ0(~A).,anddenotes the n-th Bessel function.In addition,

where γ1=a1-a3,γ2=a2-a1,and γ3=a3-a2,and

In Fig.2(a),we find that finite DMI opens a gap,thereby endowing the magnon bands with a nontrivial topology.Based on Eq. (8), we see that the effect of circularly polarized light can result in a gapped system. The interplay between the DMI and light can induce closing and reopening of the band gap. In Fig.2(b),we show that the critical points where the interplay makes the energy gap are closed.

Fig.2. Bulk magnon bands for momenta in the y direction for D=0.1J when(a) ~A=0 and(b) ~Acritical ≈2.5J.
3. Berry curvature and Chern number
The Berry curvature for the n-th magnon band can be calculated from

The summation is over all occupied bands below the bulk gap,and ?vx(y)is the velocity operator along the x(y)direction. Enis the eigenvalue of the system(Eq.(8)). In Fig.3,we show the Berry curvature of the lower band at D=0.1J for the varying light parameter ~A. We can see that the Berry curvatures change with ~A. We find that the Berry curvature increases as ~A increases for ~A <~Acriticalwhile the reverse occurs for~A >~Acritical. The associated Chern number is defined as

where the integral is over the first Brillouin zone. Consequently,the system changes from one topological magnon insulator with Chern number 1 to another one with Chern number -1. In other words, a light intensity field can lead to a topological phase transition in a topological magnon insulator.

Fig.3. Berry curvature of the lower magnon band for D=0.1J.
4. Low-energy Dirac theory
To better understand the topological properties, we present a theoretical analysis based on an effective k·p Hamiltonian.Expanding this Hamiltonian around the Dirac points to δk,we obtain the effective Dirac Hamiltonian as

where η =±1 corresponds to the two Dirac points,are the Pauli matrices of the sublattice pseudospin,t=,and Δdm=3 DS.The system can be described by a static Hamiltonian in the high-frequency regime.[15,27]Then, the static time-independent Hamiltonian is written as

The band dispersion relationship of the above Hamiltonian is
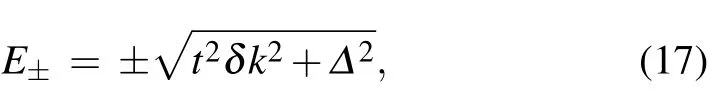
and the the corresponding wave functions are
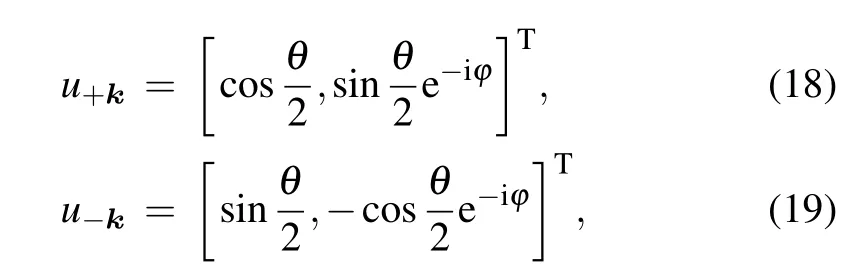

One sees that an extra light-induced term A2t2/ˉhω is introduced, and its sign depends on the polarization of light. This new term is clearly different from the intrinsic DMI term,and it can be defined as the light-induced effective DMI.The overall value of the DMI will decrease(increase)if the DMI term and the polarization of light have the same(different)sign.For the same sign, the critical point is defined at Δdm-A2t2/ˉhω where the overall DMI vanishes and the band gap closes. For example,when increasing the circularly polarized light intensity, figure 2 shows a band gap closing. The Dirac theory is consistent with the results from tight-binding theory.
The direct correspondence between the Chern number and the Hall conductance for 2D system is characterized by σxy=Ce2/h. The band gap(Δdm-A2t2/ˉhω)is closed and reopened for fixed Δdmwhen varying A,and the direction of the Hall current is changed. Therefore, the direction of the Hall current can be controlled by illuminating with light due to the fact that they lead to the change in sign of the Berry curvature of the valence band. It should be noted that in our paper, we only consider ω >0. When ω <0,Δdm-A2t2/ˉhω >0. The band will not close and reopen. The topological phase transition and change in direction of the Hall current will not occur.
5. Conclusion and summary
To conclude, we analyzed the topological properties of magnon in an insulator on a honeycomb lattice with DMI under the application of a circularly polarized light. We employed Brillouin-Wigner theory to obtain the tight-binding model with a circularly polarized light at the high-frequency regime. We found that the light can induce the closing and reopening of the band gap. The study about the corresponding Berry curvature and Chern number confirmed the lightinduced topological phase transition. We obtained the lowenergy Dirac model to better know the topological properties. The topological phase transition was light-induced handedness-dependent. The effective DMI and intrinsic DMI were responsible for the topological phase transition.
- Chinese Physics B的其它文章
- Wavelength dependence of intrinsic detection efficiency of NbN superconducting nanowire single-photon detector?
- Artificial solid electrolyte interphase based on polyacrylonitrile for homogenous and dendrite-free deposition of lithium metal?
- Effects of CeO2 and nano-ZrO2 agents on the crystallization behavior and mechanism of CaO-Al2O3-MgO-SiO2-based glass ceramics?
- Modulation of magnetic and electrical properties of bilayer graphene quantum dots using rotational stacking faults?
- Thermal conductivity characterization of ultra-thin silicon film using the ultra-fast transient hot strip method?
- Thickness-dependent magnetic anisotropy in obliquely deposited Fe(001)/Pd thin film bilayers probed by VNA-FMR?

