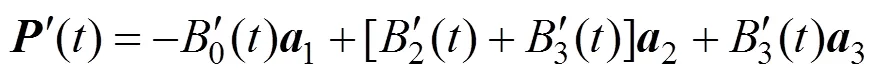吳榮軍
一類三角Bézier曲線的形狀特征
吳榮軍
(西安郵電大學理學院,陜西 西安 710121)
在幾何造型的許多應用中,良好的曲線形狀應該消除不必要的奇點和拐點,因此往往需要預知與分析參數曲線的各種形狀特征,以避免出現奇異形狀的設計風險。為了快速確定參數曲線的形狀特征,利用錐面的齊次性簡化了參數曲線的形狀條件,得出了一類帶2個形狀參數的二次三角Bézier曲線的尖點條件錐和2張重結點邊界條件錐;3張特征錐面及其切平面將特征空間劃分為不同的特征區域。曲線的形狀特征完全由特征點在特征空間的分布區域決定。用垂直于坐標軸的平面切割特征空間,可得到基于包絡與拓撲映射方法的所有形狀條件分布圖。進而討論了形狀參數變化對各特征區域的影響,相關結果可使設計者明確如何配置控制頂點或者調節形狀參數,使得生成曲線為全局凸或局部凸曲線,或具有所需要的奇點與拐點,或將當前曲線形狀調節為另一種所需的形狀。
三角Bézier曲線;形狀特征;尖點錐;重結點錐
參數曲線的形狀特征,主要指曲線的奇點、拐點及凸性。其幾何特征的判定條件對于參數曲線的形狀控制與調節具有重要作用。與之密切相關的主要研究有仿射不變量方法[1]、基于包絡和拓撲映射的方法[2]和基于控制頂點軌跡的幾何刻畫方法[3]。形狀分析法[4-6]對基于包絡和拓撲映射的方法做了補充,在相應的形狀條件分布圖中區分出了全局凸和局部凸區域。3種方法對曲線形狀特征的分析都需要假設某2個邊向量是不平行的,實際上,文獻[3]在仿射不變量方法提出后,就曾設想能否去掉平行假設,但也沒有解決這一問題;特征空間方法[7]得出了一系列造型曲線的形狀特征判斷條件,其判斷不需要平行假設。本文討論一類帶形狀參數的二次三角多項式Bézier曲線[8-9]的形狀特征,得出的特征空間與已有的Bézier型曲線[7]的特征空間結構類似,不同之處在于,其尖點錐的切平面方程含有形狀參數,從而使得該曲線形狀參數的調節能力優于諸多帶形狀參數的Bézier型曲線[7]。
1 三角帶參Bézier曲線簡介
2 尖點條件錐
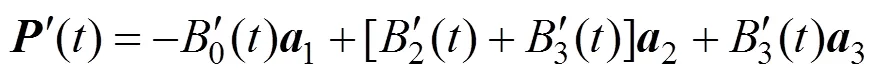
實際上,由及還可分別得到形式的尖點條件線
《失業保險條例》規定的失業保險保障對象為城鎮企業事業單位職工,京津冀一體化背景下河北省城鎮化步伐不斷加快,而新生代農民工成為城市職工當中的一員,然而,高失業率的新生代農民工對政策了解甚少,出現“應保未保”、“待遇水平低”以及“跨區轉移困難”等問題,加深了農民工群體的就業困境。因此,建立長效機制的農民工失業保險政策應重視農民工需求,保障農民工的權益,能有效為農民工解決后顧之憂,不但讓其“進得來”,還要“留得下”。新型城鎮化不僅是戶籍的城鎮化,更重要的是讓農民工與城鎮居民同等享有國家政策,給新生代農民工落戶城鎮提供更多的機會。
及
如果將、及看作三維空間的點,那么分別以3點為末端,以原點(0,0,0)為起點所構成的向量是相互平行的,并且都與經過點
(2)
和原點的直線平行。受該性質啟發,構造以這些直線為母線的錐面,由式(2)消去參數t可得到錐面方程,,y,c2<0或00,那么用–d作為新的特征點進行判斷即可,從而可使特征點位置的判斷大為簡化(以下討論僅限于下半空間)。
對高速公路橋梁進行養護這樣的工作對專業度有要求,公路橋梁出現問題,并不是只要能夠把損毀給彌補就可以了,還要考慮到多個方面的問題,比如如何使用最低的成本來保證養護的質量,如何讓公路橋梁的養護工作帶來的影響降到最低等等,這些都需要專業的養護人員來解決。
6.4 形狀參數對特征空間的影響
首先,因為重結點邊界錐的切平面的方程式不含形狀參數,所以形狀參數變化不影響全局凸區域(如圖6左下區域所示);從而可知,當曲線的控制多邊形為全局凸[6]時,無論如何調節形狀參數,曲線始終保持全局凸。
(a) λ=μ=1
(b) λ=μ=0.5
(c) λ=μ=–0.5
圖6 形狀參數變化對特征空間的影響
如圖6所示,改變形狀參數,可對3張特征錐面及切平面ci進行調節。注意到切平面c1與切平面π2的交線為x軸,當參數減小時,切平面c1與π2的夾角隨之減小,當時,c1的極限位置就是π2;類似的有,切平面c2與切平面π1的交線為軸,當參數減小時,切平面c2與π2的夾角隨之減小,當時,c2的極限位置就是π1。當時,尖點錐Fc的極限位置為切平面π1與π2,重結點邊界錐F1的極限位置為切平面π2,重結點邊界錐F2的極限位置為切平面π1。所以隨著形狀參數(或)減小,重結點區域L、雙拐點區域I2以及局部凸區域相應縮小;全局凸區域N01及單拐點區域相應擴大。
本文所得曲線的特征空間,與已有Bézier型曲線[7]的特征空間結構類似,除了具體方程外,最大不同之處在于,通過形狀參數調節尖點錐在邊界處的切平面c1和c2,可對雙拐點區域I2及重結點區域L進行壓縮。
圖7(a)~(c)對應的控制頂點為b0=[0,0]T, b1=[2,2]T,b2=[0,2]T,b3=[1,1.5]T;相應曲線形狀變化說明,當控制多邊形是局部凸[6]時,改變形狀參數可以將曲線形狀調節為局部凸。
圖7(d)~(i)中對應的控制頂點為b0=[0,0]T,b1=[2,2]T,b2=[0,2]T,b3=[2,0]T;相應曲線形狀變化說明,當控制多邊形的首末2邊相交時,通過修改形狀參數可以將曲線的形狀調節為全局凸;圖7(d)~(i)的變化顯示了同時減小形狀參數及時,切平面對區域的壓縮,使得特征點屬于全局凸區域N01 (如圖6所示)。
(a) 尖點(λ≠μ)(b) 重結點(端點)(c) 局部凸 (d) 重結點(內部)(e) 尖點(λ=μ)(f) 2個拐點 (g) 1個拐點(區域S2)(h) 1個拐點(區域S1)(i) 全局凸
圖7 三角Bézier曲線的形狀特征
而已有的諸多Bézier型曲線[7]都不具備這種調節能力,因為其尖點錐的2張切平面分別是及(如圖6(a)所示)。圖7(g)~(h)說明當控制多邊形的首末2邊相交時,可通過調節形狀參數使得特征點屬于單拐點區域S1 (圖7(h))或S2 (圖7(g))。圖7中的各曲線的特征判斷見表1 (其中特征點的計算利用了6.3的簡化性質)。
上述討論表明,當特征點屬于切平面c1與π2 (或者切平面c2與π1)所圍成區域內部時,可通過形狀參數對曲線P(t)的形狀特征進行一定程度的調節,特征點越靠近切平面πi,形狀參數的調節能力越強,曲線可選擇的形狀特征越多。
第五個支出是社會保障支出,關于社會保障支出的主要有以下幾個問題:社會保障支出總量不足;社會保障支出增長緩慢;社會保障支出結構不合理、地區差異顯著;社會保障基金增值困難、安全隱患。這個具體的數據大概說一下:2010年的時候我們國家社會保障支出占GDP的2.28%。這個與同期國家比較,比如說以中等發達國家為例,中等發達國家社會保障支出比重是30%,我們是2.28%,社會保障構建上嚴重投入不足,今天我們所講的全民享有的、能夠覆蓋13億人口的社會保障體系尚未完全建立起來。
表1 圖7中相關曲線的特征判斷
序號特征點形狀參數區域判斷特征區域 (a)(–1,–3,–4)λ=0.4927554, μ=1Fc=0尖點錐 (b)(–1,–3,–4)λ=0.9609671, μ=1F2=0重結點區域 (c)(–1,–3,–4)λ=1, μ=0.25F2<0, π1>0局部凸區域 (d)(–4,–8,–4)λ=1, μ=1Fc<0, F1>0, F2>0重結點區域 (e)(–4,–8,–4)λ=0.707107, μ=0.707107Fc=0尖點錐 (f)(–4,–8,–4)λ=0.25, μ=0.25Fc>0, c1<0, c2<0雙拐點區域 (g)(–4,–8,–4)λ=–0.25, μ=0.25c1<0, c2>0單拐點區域 (h)(–4,–8,–4)λ=0.25, μ=–0.25c1>0, c2<0單拐點區域 (i)(–4,–8,–4)λ=–0.25, μ=–0.25c1>0, c2>0全局凸區域
7 結束語
本文討論了帶2個形狀參數的二次三角多項式Bézier曲線的形狀特征判斷問題,得到了該曲線的特征空間,各特征區域由尖點錐和重結點邊界錐及其切平面對三維空間劃分而成,特征點由控制多邊形邊向量對應的二階行列式構成,區域判斷只涉及特征點關于錐面及平面的代入計算,因而非常適合于計算機程序自動判斷;并進一步分析了形狀參數對特征錐及其切平面的調節作用。
參考文獻
[1] SU B Q, LIU D Y. An affine invariant theory and its application in computational geometry [J]. Scientia Sinica,Series A, 1983, 26(3): 259-272.
[2] 葉正麟. 一類平面B-樣條曲線的形狀分類[J]. 純粹數學與應用數學, 1990, 6(1): 72-74.
[3] STONE M C, DEROSE T D. A geometric characterization of parametric cubic curves [J]. ACM Transactions on Graphics, 1989, 8(3): 147-163.
[4] 吳榮軍, 葉正麟, 羅衛民. 有理C-Bézier曲線的形狀分析[J]. 計算機學報, 2007, 30(11): 2055-2059.
[5] 吳榮軍. 平面三次H-Bézier曲線的形狀分析[J]. 應用數學學報, 2007, 30(5): 816-821.
[6] 吳榮軍, 彭國華, 羅衛民, 等. 四次帶參Bézier曲線的形狀分析[J]. 計算機輔助設計與圖形學學報, 2009, 21(6): 725-729.
[7] 吳榮軍. 參數曲線形狀分析的特征空間方法研究[D]. 西安: 西北工業大學, 2015.
[8] HAN X L. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7): 503-512.
[9] 吳曉勤, 韓旭里, 羅善明. 帶形狀參數的二次三角Bézier曲線[J]. 工程圖學學報, 2008, 29(1): 82-87.
[10] 徐迎博, 喻德生. 帶形狀參數的二次三角多項式Bézier曲線形狀分析[J]. 浙江大學學報:理學版, 2013, 40(1): 35-41.
Shape Features of a Kind of Trigonometric Bézier Curve
WU Rong-jun
(School of Science, Xi’an University of Posts and Telecommunications, Xi’an Shaanxi 710121, China)
Abstract: In many applications of geometric modeling, curves of desirable shape should eliminate the unnecessary singularities and inflection points. Therefore, to avoid potential risk in shape design, it is essential to predict and analyze the shape features of parametric curves. In order to quickly determine the shape features of parametric curves, the shape conditions of the parametric curve are simplified due to the homogeneous property of cones, and the cusp conditional cone and two boundary loop conditional cones are obtained for a quadratic trigonometric polynomial Bézier curve characterized with two shape parameters. These three characteristic cones and their tangent planes divide the characteristic space into different characteristic regions. The curve's shape features are completely determined by the distribution region which the characteristic point locates in the characteristic space. It is shown that the shape diagrams obtained by the method based on the theory of envelopes and topological mappings can be derived from characteristic space by virtue of planar slices, which are vertical to one of the axes. Furthermore, the influences of shape parameters on the associated characteristic regions are also discussed. The obtained results enable the user to place control points or choose shape parameters so that the resulting curve is globally or locally convex, possessing wanted singularities or inflection points, or enjoying the desired shape features.
Keywords: trigonometric Bézier curves; shape features; cusp cones; loop cones
中圖分類號:TP 391
DOI:10.11996/JG.j.2095-302X.2019030549
文獻標識碼:A
文章編號:2095-302X(2019)03-0549-07
收稿日期:2018-11-15;
定稿日期:2018-12-18 基金項目:陜西省教育廳專項科研項目(14JK1655);陜西省自然科學基礎研究計劃項目(2018JM1054) 第一作者:吳榮軍(1975-),男,陜西白水人,講師,博士。主要研究方向為計算機輔助幾何設計、數值分析等。E-mail:wrj2140@163.com