玩轉立方體

王耀楊

挑戰立方體

看到這篇文章的標題，相信很多同學都會感到奇怪：立方體？我早看得不能再熟悉了！還有什么可玩的呢？

不要得意得太早哦，在這篇文章里，我們將嘗試從一個全新的視角來欣賞立方體，并且由此提出一系列有趣的問題。試試看，你能解決其中幾個問題？

讓我們從立方體的體對角線方向去觀察它。如圖①，一個立方體有4條體對角線，選取其中任意一條，沿此方向正投影，會得到一個正六邊形。這個正六邊形由3個彼此全等的菱形組成，每個菱形都是一個正方形面的投影。

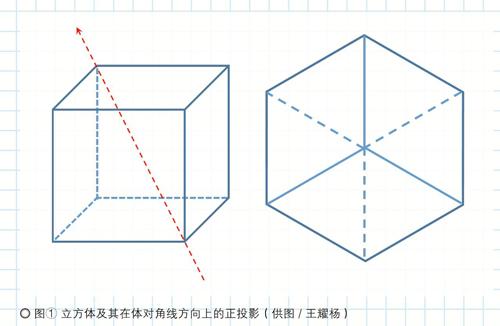
我們的第一個問題，就從這里開始：如果只用一只眼觀察，最多同時可以看到不透明立方體的幾個面，為什么？如果關注的對象是棱，那么最多同時可以看到幾條棱，為什么？

第二個問題需要先定義“挖洞”的概念。當我們說“在一個立體圖形上挖洞”時，意思是去掉一部分圖形，同時保持剩余部分仍然具有一個完全的封閉形態，而不是類似“U”形。更進一步，當我們說“從挖好的洞中穿過”時，意思是在不超過洞邊界的范圍內行進，整個過程中不能破壞洞的邊界。當然，我們始終假設所研究的圖形都是剛性的，不會像橡膠那樣發生彈性形變。現在問題來了：是否有可能在一個立方體中挖一個洞，使得另一個與它全等的立方體能夠從洞中穿過去呢？

第三個問題：二維國的立方體來客。

1884年，一位英國牧師艾伯特寫了一本名為《二維國》的小冊子。作者的創作意圖本不是宣講數學，但是在今天看來，它完全可以作為一本現代幾何學的入門科普書來讀。所謂二維國，就是平面世界，其中的居民都是平面圖形，如三角形、正方形或者圓。居民們關于空間的經驗直覺就只局限于二維。那么，我們所熟悉的三維圖形在這些居民的理解中會是怎樣的存在呢？

設想一位立方體先生到二維國親戚家拜訪，后者當然無法窺見立方體的全貌，而只能看到立方體穿過二維平面時所截得的“側影”。例如，當立方體的一組棱垂直于平面時，截得圖形恒為正方形;當立方體的面對角線垂直于平面時，留下的是寬度不斷變化的矩形“側影”，如圖②：穿入和穿出瞬間時，退化為線段的形態，其間最大矩形截面的長寬比為為。

現在問題來了：如果令立方體的體對角線垂直于平面，則穿行時所留下的“側影”會如何變化？

在各位讀者自己開始研究之前，這里有一個建議。你要保證手頭有一個立方體的實物模型，最好是透明的;比如用小細棍和膠泥之類的材料做一個，便于觀察。上面這幾個問題幾乎都是基于觀察具體實物來研究的，當然，你還需要解釋其中的道理。

藝術家與立方體迷思

在給出問題1的解答之前，我要先考考讀者們，你們能否想象，對這個問題的追問和深思居然激發了一群藝術家的創作靈感？難道說藝術家們也都很喜歡數學？

問題1的答案是：最多同時看到3個面;最多同時看到9條棱。

立方體的6個面可以分成3組，每一組都有彼此相對，即沒有公共點的兩個平行面。從體對角線方向可以同時看到3個面，我們來證明不能看到更多。假設可以看到4個面，則必定有一組平行面同時被看到，但這是不可能的。設想它們是發光的（“看到”的物理原理就是來自被看物體的光子進入人眼），則一組平行面照亮的空間區域分別位于兩個平行平面的一側，而這兩個區域沒有公共點，如圖③所示。換言之，空間中任何位置都不能同時看到這兩個面。因此3個就是能同時看到的最多面數。

由前面的分析可知，3組中每組都至少有一面是看不到的，這3個看不到的面兩兩相交得到的3條棱肯定也是看不到的，因此最多同時看到12-3=9條棱。沿體對角線方向確實可以看到9條棱，因此9條是能同時看到的最多棱數。

但是這與藝術創作有何關聯呢？原來，20世紀初的藝術家們也采納了將現實物體分解成局部要素的幾何思維，但是他們不滿足于用只能看到有限個側面的單一視角呈現，而是嘗試將多視角的景象在同一個畫面中展示出來。這就是影響深遠的立體派（Cubism），這一思潮首先影響的是畫家和雕塑家，很快又波及到文學、音樂和建筑領域。

圖④給出了立體派代表人物畢加索的兩幅作品。其中左圖是較早的作品《彈曼陀鈴的少女》，可以看到原本婉轉流暢的線條都呈現為看似彼此割裂而抽象的幾何圖形;右圖則是相對晚一些的作品《靜物》，畫面看似混亂，是因為畫家將原本不可能從任一視角看到的各種細節全都呈現出來。這兩幅作品可以代表畢加索個人思考的兩個階段：前者是“分析”的時期，后者則是“綜合”的時期。

問題2需要一點初中水平的數學計算。前文提到過，將立方體沿體對角線方向投影，可以得到一個正六邊形。如圖⑤，為不失一般性，設立方體邊長為1，則正六邊形的較短對角線（垂直于視線方向的面對角線保持原長），如圖建立直角坐標系，則有。由此確定直線方程，代入坐標驗證，可知A點位于AB下方;結合對稱性可知正方形位于正六邊形內部。將圖示正方形對稱地擴大一點點，還可以位于正六邊形內部，由此可以保證原正方形可以從中穿過去。

讓一個高度對稱的立體圖形從自身之中穿過去，乍看起來似乎是匪夷所思的，但是上面這個例子恰好使我們意識到立方體具有一種特別的對稱性：體對角線。不難想象，如果將立方體換成具有完美對稱性的球，那么問題2就無解了。因此不妨說，立方體能夠實現這個結果，恰恰是因為它還不夠對稱。按照這一思路，那么正四面體也可以穿過自身嗎？請讀者自己尋找答案吧。

問題3相當于考察垂直于體對角線的不同平面截立方體所得的圖形。最開始是一個點，接著變成正三角形并逐漸放大，正三角形的面積達到最大后各頂點內縮而變成六邊形，到恰好正中間位置時截面是一個正六邊形;后一半變化過程是對稱的，如圖⑥。

在今天，如果一位數學教師對艾伯特牧師的《二維國》感到格外欣賞，主要原因很可能是因為它為初學者探索四維幾何學打開了一扇門。一位二維國居民能夠以何種方式去思考和理解三維世界來的客人，恰如我們三維智慧生物可以如何去思考和理解四維的存在。

如果你以為四維幾何是只有數學家們才會關注的奇思妙想，圖⑦中的畫作可能會令你大吃一驚。1954年，超現實主義畫家達利完成了一幅前所未有的《耶穌受難》，這可能是同主題作品中最具視覺沖擊力的一幅，因為其中出現了四維立方體在三維世界中的“展開圖”。正如三維立方體的展開圖是由6個正方形構成的平面圖形，四維立方體的展開圖是由8個三維立方體構成的立體圖形—你不妨試著想想它“拼合”起來的樣子（如圖⑧）！

各位讀者，相信你們已經看到，立方體的體對角線是一個極為特別的視角;從這個角度考察立方體，會出現很多有趣的新問題和新成果。作為本文的結束，這里給出一個趣味問題供有興趣的讀者研究吧。圖⑨給出一個立方體型電阻，它的每條棱都是阻值為1歐姆的電阻，在體對角線兩端連接外部電路，則整個立方體可以視為一個復合電阻。根據立方體的對稱性質分析一下，它相當于多少歐姆的電阻呢？

答案與解析：5/6歐姆。假設整體復合電阻的外接端點是A和B，則由幾何對稱性可知A的

3個相鄰端點確定了一個等電勢面，位于A與等電勢面之間的3個1歐姆電阻相當于并聯關系，因此相當于一個1/3歐姆的電阻;下一個等電勢面是，它與面之間的6個單位電阻相當于并聯關系，因此等價于一個1/6歐姆的電阻;類似地，面與頂點B之間也相當于一個1/3歐姆的電阻。因此總電阻為1/3+1/6+1/3=5/6歐姆。

（責任編輯/陳瑩? 美術編輯/胡美巖）