數據的正態性檢驗及Excel/SPSS/Stata 軟件的實操應用

陳 軍

（新疆師范大學 商學院，新疆 烏魯木齊 830017）

1 數據正態性檢驗的相關理論

多數統計檢驗都要求數據滿足正態分布，特別是針對小樣本。如果誤差項不服從正態性假定，雖然可以利用最小二乘法進行參數估計，但卻無法進行檢驗和預測。如果解釋變量不能很好地匹配因變量的峰度和偏度，將會導致樣本性質中的統計推斷結果發生偏差。實際情形中，出于樣本可獲得性的考慮，通常采用對數據進行變換的方法，將其數據轉換成正態分布，但應該注意到，在數據轉換的同時已將數據蘊含的原始信息發生了改變。由此得到的回歸結果，其參數的意義解釋也已和變換前有所改變。

數據正態性檢驗的方法主要有兩類：使用圖形進行大致的判斷以及使用統計檢驗。圖形檢驗中常用的是直方圖和正態分位數圖。如果得到的數據直方圖和鐘形相差很大，則拒絕正態性分布，這是一種非常直觀的方法，實用性強。使用統計檢驗多基于卡方統計量，實質是根據下表1 中標注的區間找到落在該區間內的實際觀測值個數和期望觀測值個數，然后進行卡方檢驗。

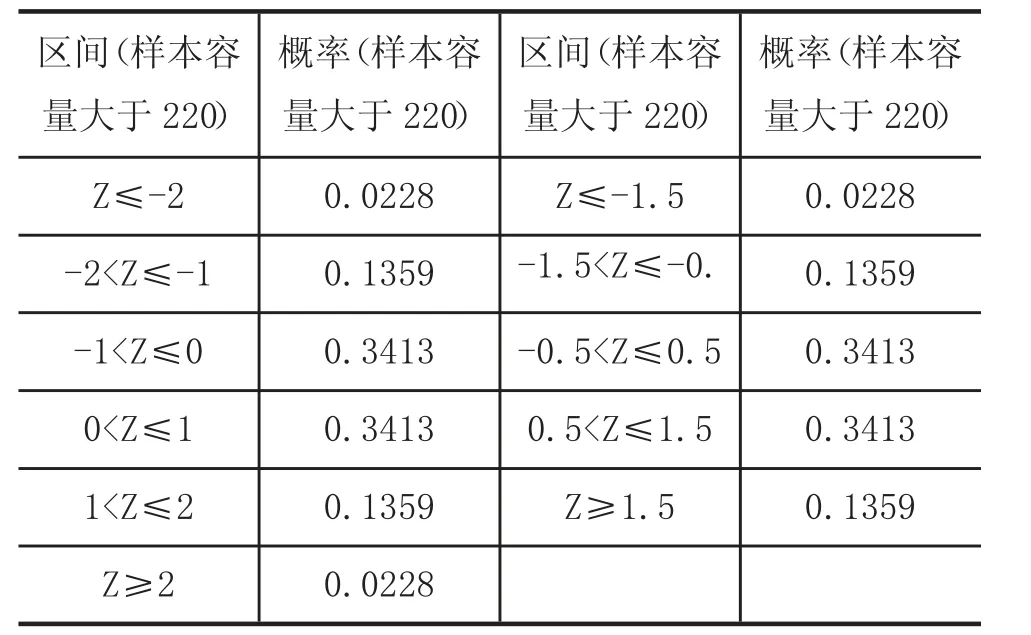
表1 卡方檢驗區間劃分

數據正態性的其他統計檢驗，包括偏度-峰度檢驗、D′Agostino 檢驗、Shapiro-Wilk w 檢驗和Shapiro-Francia w′檢驗。應該注意，隨著樣本量的增大，所有的統計檢驗趨于拒絕原假設，而圖形、偏度及峰度的數值分析可能更有利于研判數據正態性狀況。

2 Excel 對于數據正態性的檢驗

Excel 對于數據正態性的檢驗方法相對單一，一般采用繪制正態概率圖。如果標準正態概率圖中的點基本圍繞在一條直線周圍，那么可以說該組數據基本服從正態分布。下面結合具體的例題進行。

例：某車間加工一批零件尺寸如下表2，請問零件尺寸是否呈正態分布。

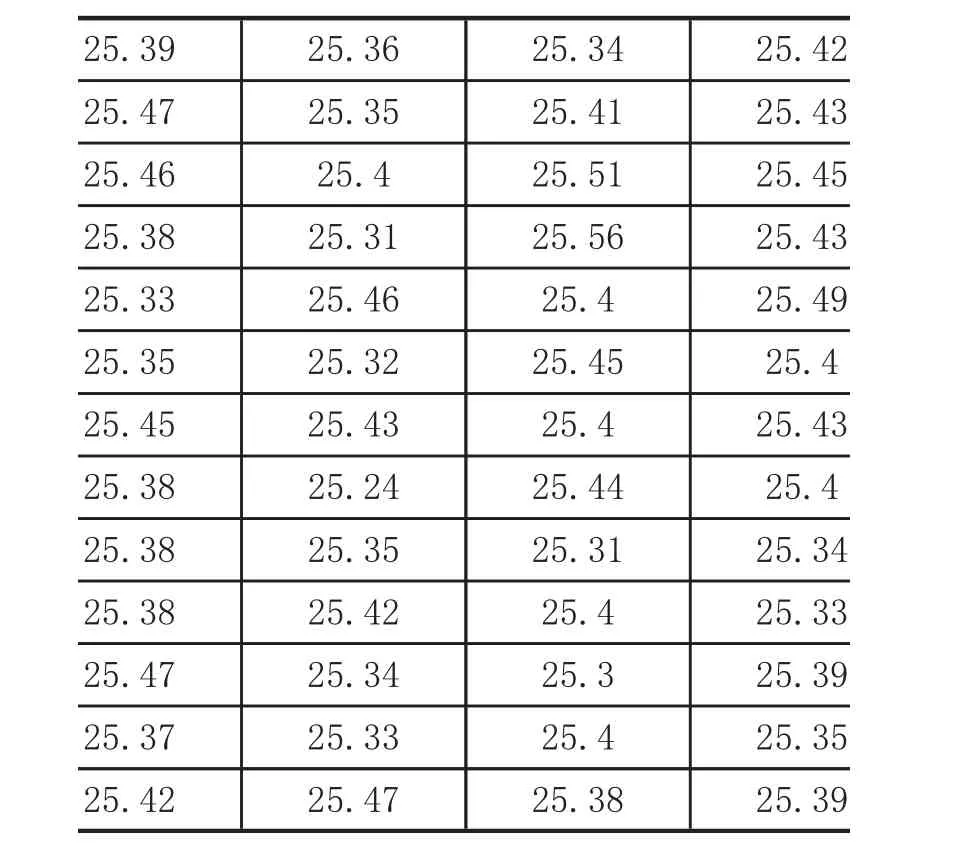
表2 車間加工的零件尺寸數據 單位：毫米

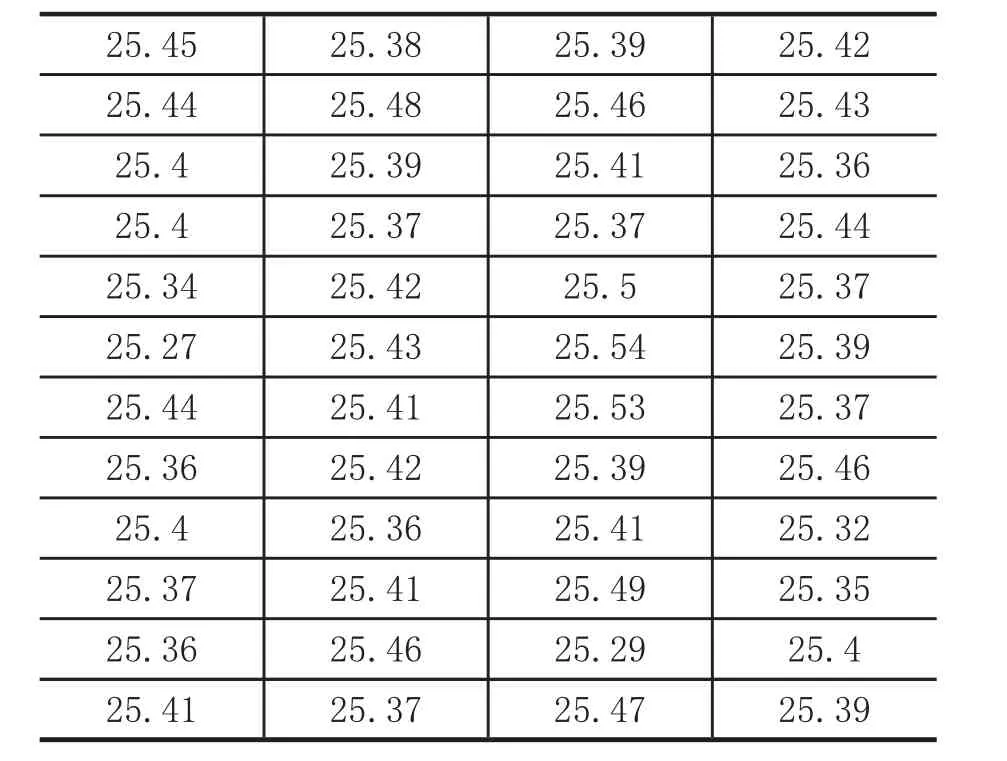
25.45 25.38 25.39 25.42 25.44 25.48 25.46 25.43 25.4 25.39 25.41 25.36 25.4 25.37 25.37 25.44 25.34 25.42 25.5 25.37 25.27 25.43 25.54 25.39 25.44 25.41 25.53 25.37 25.36 25.42 25.39 25.46 25.4 25.36 25.41 25.32 25.37 25.41 25.49 25.35 25.36 25.46 25.29 25.4 25.41 25.37 25.47 25.39

【實驗操作步驟】

Step1：將表格數據按照升序排序成一列。

Step2：計算（j-0.5）/100。

Step3：根據（j-0.5）/100=P（Z），求出正態分位數。單擊D2 單元格，選擇“公式-〉插入函數”。在“插入函數”對話框，“選擇類別”選取“統計”，“選擇函數”選擇“NORM.S.INV”,點擊“確定”。結果見下圖1。

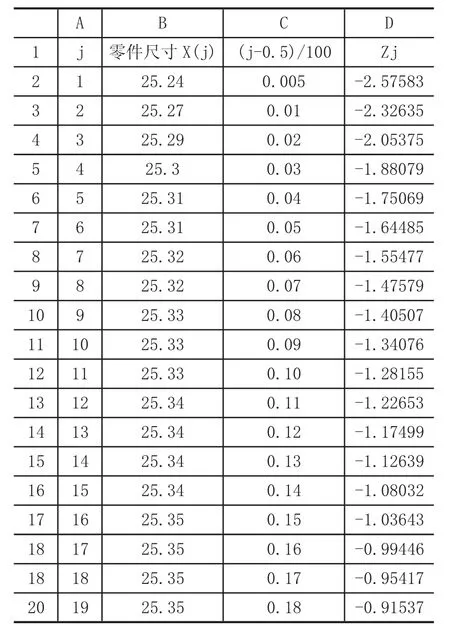
圖1 正態分位數及標準正態分位數計算結果

Step4：，選擇“數據-〉數據分析”，在“分析工具”中選擇“回歸”，單擊“確定”。以Zi 為縱軸，X（j）為橫軸，繪制標準正態概率圖。然后單擊“確定”，得到標準正態概率圖，如圖2 所示。其中，X（j）轉化為其對應的百分比排位。可以看出，由（X（j），Zi）形成的點基本圍繞在一條直線周圍，可以說該組數據基本上服從正態分布。

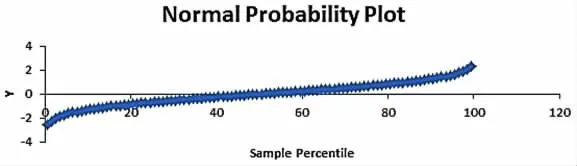
圖2 標準正態概率圖

3 SPSS 軟件對于數據正態性的檢驗

SPSS 軟件對于數據正態性的檢驗是建立在數據分布直方圖的基礎上，可采用多種檢驗方法。為比較方便，案例數據同上例。

【實驗操作步驟】

在SPSS 里執行“分析-〉描述統計-〉頻數”（菜單見下圖，英文版的可以找到相應位置），然后彈出一個對話框，變量選擇左邊的“零件尺寸”，再點下面的“圖表”按鈕，彈出圖中右邊的對話框，選擇“直方圖”，并選中“包括正態曲線”。點擊“繼續”、“確定”按鈕。數據分布直方圖如下圖3。

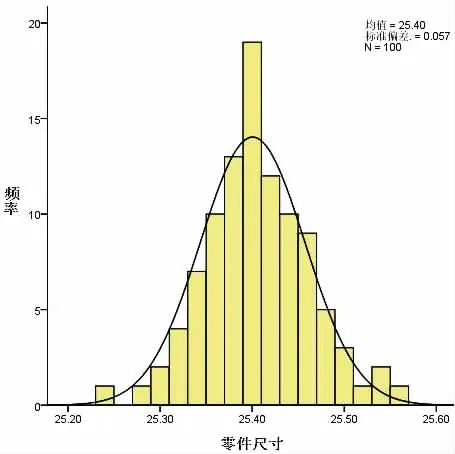
圖3 輸出的正態分布圖（直方圖）

圖中橫坐標為期零件尺寸，縱坐標為分數出現的頻數。從圖中可以看出根據直方圖繪出的曲線是很像正態分布曲線。如何證明這些數據符合正態分布呢，光看曲線還不夠，還需要進一步檢驗。

（1）檢驗方法一：看偏度系數和峰度系數

Step1：在“頻率”對話框，點擊“統計量”按鈕，選取如下復選框。點擊“繼續”、“確定”按鈕。選項界面見下圖4。

圖4 頻率：統計量對話框及輸出統計量結果

Step2：從“統計量”結果中，看到“偏度”為0.113，“峰度”為0.505，均小于1，可認為近似于正態分布。

（2）檢驗方法二：單個樣本K-S 檢驗

操作步驟：在SPSS 里執行“分析-〉非參數檢驗-〉單個樣本K-S 檢驗”，彈出對話框，檢驗變量選擇“零件尺寸”，檢驗分布選擇“常規（正態分布）”，然后點“確定”。結果如下圖5。

圖5 單樣本K-S 檢驗對話框及輸出結果

從結果可以看出，K-S 檢驗中,Z 值為0.735，P 值(sig 2-tailed)=0.652〉0.05，因此數據呈近似正態分布。

（3）檢驗方法三：Q-Q 圖檢驗

操作步驟：在SPSS 里執行“分析-〉描述統計-〉Q-Q 圖”，彈出對話框，變量選擇“零件尺寸”，檢驗分布選擇“正態”，其他選擇默認，然后點“確定”，最后可以得到Q-Q 圖檢驗結果，結果很多，我們只需要看最后一個圖，見下圖6。

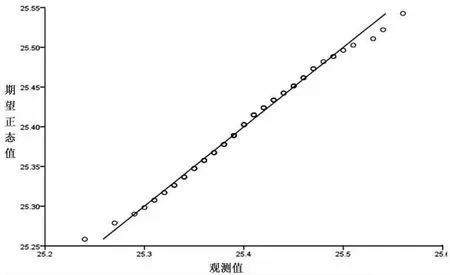
圖6 Q-Q 圖檢驗結果(零件尺寸的正態Q-Q 圖)

QQ Plot 中，各點近似圍繞著直線，說明數據呈近似正態分布。

4 Stata 軟件對于數據正態性的檢驗

Stata 軟件對于數據正態性的檢驗方法主要有分位正態圖、正態性統計檢驗。為比較方便，案例數據同上例。

（1）檢驗方法一：分位正態圖

分位正態圖的繪制命令格式如下：Qnorm varname[if][in][,options]

該命令的大部分選項都是繪圖命令所共有，獨有選項是grid,加入grid 項可以在圖中依次標 注 0.05、0.10、0.25、0.50、0.75、0.90、0.95百分位的坐標刻度。分位正態圖將觀測變量分布的分位數與一個具有相同平均數和標準差的理論正態分布的分位數進行比較，通過比較偏離程度進行直觀研判正態性狀況。

Step1：打開數據文件。

Step2：在“command”區域輸入如下命令：.qnorm size,grid

回車，執行結果如下：

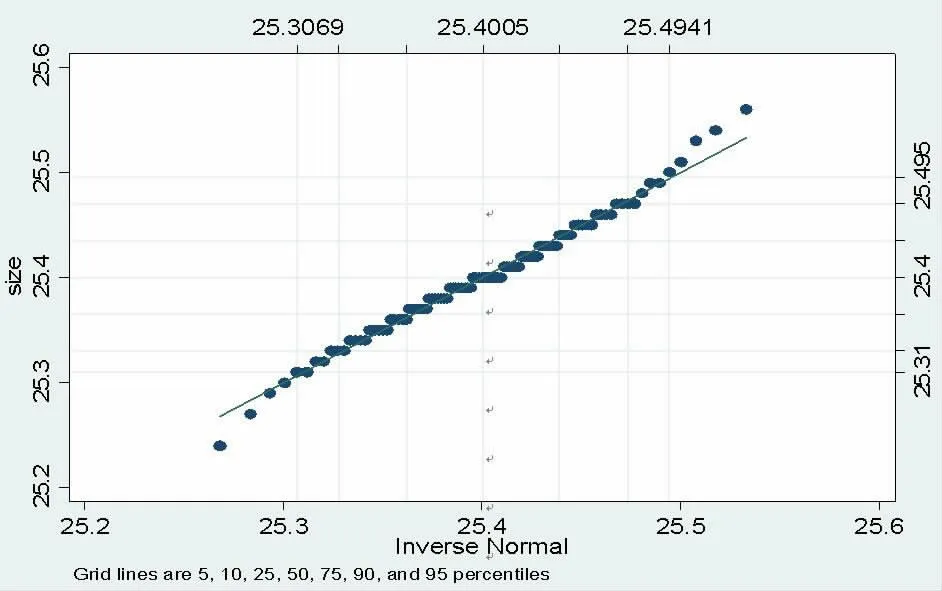
圖7 size 的分位正態圖

與完全正態分布相比（圖中對角線），數據分布近似呈現正態性。

（2）檢驗方法二：正態性統計檢驗

【實驗操作步驟】

Step1：打開數據文件。

Step2：在“command”區域輸入如下命令：sktest size

回車，執行結果如下：

結果顯示峰度、偏度檢驗以及峰度-偏度合并檢驗都表明呈現正態性(P 大于0.05)。

Step3：在“command”區域輸入如下命令：lnskew0 size2=size回車，執行結果如下：

Step4：在“command”區域輸入如下命令：.swilk size

回車，執行結果如下：

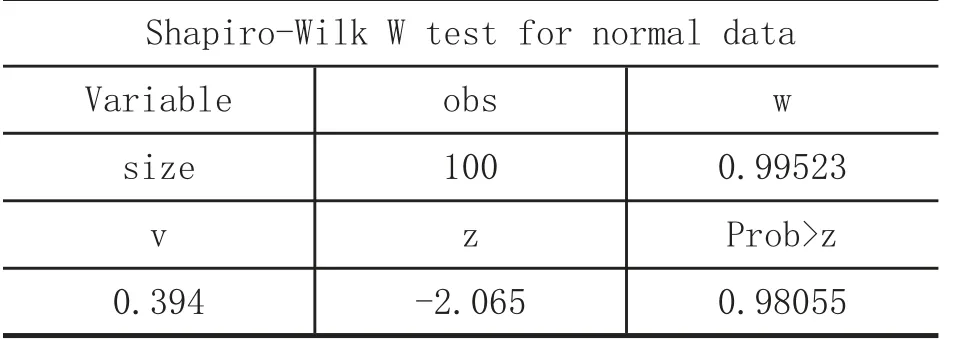
Step5：在“command”區域輸入如下命令：swilk size2,lnnormal

回車，執行結果如下：

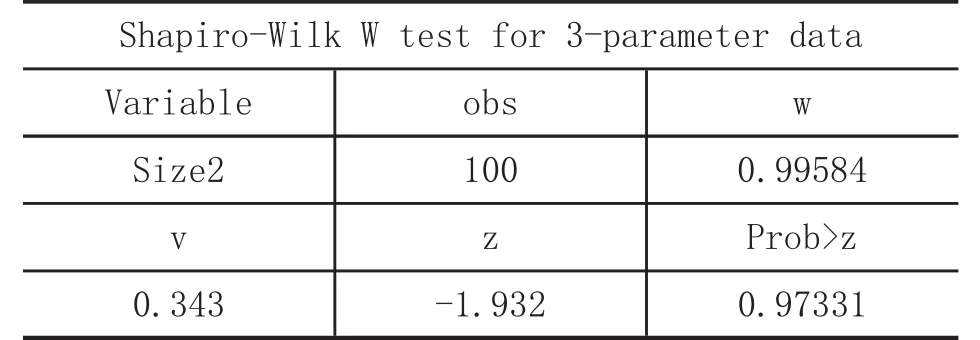
結果顯示，同sktest 檢驗結果一樣，表明數據分布呈現正態性。需要說明的是，lnskew0 命令是為變量size 找一個k 使得ln(size-k)的偏度為0，并定義這個新的變量為size2；當對完成這一變換的變量進行swilk 檢驗時，需要加入lnnormal 選項。

Step6：在“command”區域輸入如下命令：.sfrancia size

回車，執行結果如下：

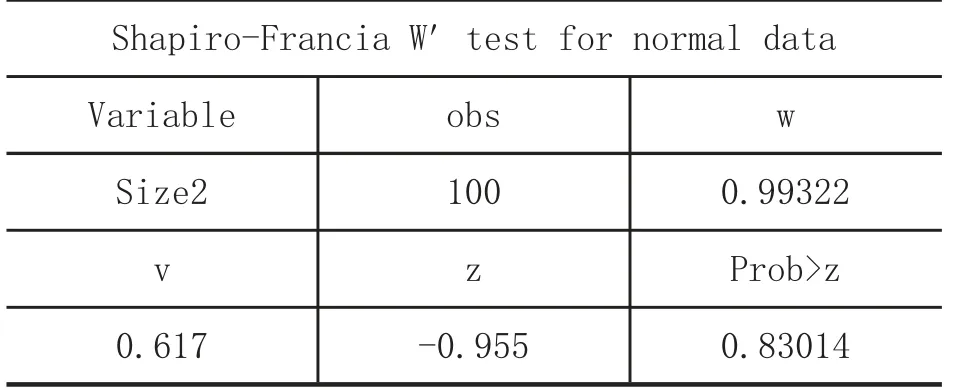
結果顯示，同sktest 及swilk 檢驗結果一樣，表明數據分布呈現正態性。

5 結語

通過上文分析，可以看到Excel、SPSS、Stata 幾種軟件都能處理數據正態性檢驗，但在具體的應用操作上存在一定差異：Excel 相對簡單；SPSS 軟件在分布直方圖基礎上檢驗方法較多；Stata 軟件的檢驗方法則更為靈活。在實際應用中，要結合數據分析對于總體正態性的要求，像方差分析就要求數據分布滿足正態性的條件，而回歸分析（特別是大樣本）則對于正態性檢驗的要求就沒有那么重要。