采樣袋法檢測汽車內飾零部件VOC及結果分析
孫成武,陳林萍,曹維福
(江淮汽車股份有限公司,安徽合肥 230022)
采樣袋法檢測汽車內飾零部件VOC及結果分析
孫成武,陳林萍,曹維福
(江淮汽車股份有限公司,安徽合肥 230022)
為滿足GB/T 27630《乘用車內空氣質量評價指南》的要求,利用采樣袋法對汽車內飾零部件VOC進行檢測和管控,采樣袋法包括預處理、氣體采集分析及結果處理3個步驟。主要介紹了對汽車內飾零部件VOC檢測結果的分析管控方式。
汽車內飾零部件;VOC;采樣袋;分析管控
Abstract:In order to meet requirement of GB/T 27630 《Guidelines to evaluate interior air quality of vehicles》,the VOC component of automotive interior trim parts was tested and controlled with the sampling bags method. Three steps of previous processing,sample collection and data analysis were included in the sampling bags method. It was focused on introducing the way of analyzing and controlling test results of VOC of automotive interior trim parts.
Keywords:Interior trim parts; VOC; Sampling bag; Analyzing and controlling
0 前言
隨著汽車工業的迅猛發展,人們停留在車內的時間越來越長,車內空氣質量也越來越受到消費者的關注和重視。車內低劣的空氣質量嚴重威脅著人們的健康,研究發現,車內的空氣污染程度有時會高于車外的10倍[1]。GB/T 27630《乘用車內空氣質量評價指南》[2]的實施使汽車生產企業更加關注汽車內飾零部件的選材和制造工藝過程,同時也更加重視車內空氣質量問題。
VOC(Volatile Organic Compounds)指揮發性有機化合物,世界衛生組織將VOC定義為:常壓下,沸點范圍在50~260 ℃間、室溫下飽和蒸氣壓超過133.32 kPa的一系列易揮發性有機化合物。汽車內部污染空氣主要來源于內飾部件VOC,包括甲醛、烷烴、苯、甲苯、二甲苯及醛類等,此類VOC易引發呼吸道以及神經系統等方面的疾病。
1 VOC檢測方法
目前VOC的檢測方法主要有以下幾種:采樣袋法、檢測艙法、項空法、熱解析法和甲醛揮發法[3]。國際上通用的檢測方法一般有歐美的檢測艙法和日系的采樣袋法,其中采樣袋法是國內VOC檢測的主流方法,主要檢測項目為苯烴類和醛類物質。
1.1 原理
模擬樣品在車內的使用狀況,將樣品放入密封袋中,充入適量氮氣,加熱,VOC氣體散發,用TENAX管吸附苯烴類物質,用ATD-GC/MS檢測。用DNPH管吸附醛酮類物質,洗脫后用HPLC檢測。實驗裝置示意圖見圖1,吸附管見圖2。
1.2 檢測步驟
檢測步驟如圖3所示。
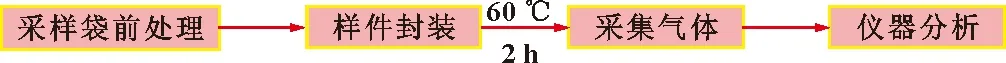
圖3 檢測步驟
(1)采樣袋前處理
先將樣袋密封后抽空樣袋內空氣,再向樣袋中充入占其容積50%左右的純氮氣(純度為99.99%以上);在60 ℃恒溫箱內放置2 h后,用真空泵迅速將袋內的氣體抽出。
(2)樣品存放及制取
①測量并記錄樣件的尺寸(mm),組合樣品按照最大樣件尺寸記錄;
②向處理過的樣袋中投入樣件后密封;
③向樣袋內充入樣袋容積30%左右的純氮氣后,用泵將氣體抽出,反復兩次;
④在25 ℃下注入樣袋容積50%左右的純氮氣。
(3)采集氣體
①輕揉裝有零件的樣袋,使內部的氣體均勻化,微開閥門,擠出管道內殘留氣體;
②在管道1上安裝TENAX管,在管道2上安裝DNPH管;
③打開管道1、管道2的閥門開始采樣;
④管道1的TENAX管采樣完成后,關閉管道1的閥門,立即將新的TENAX管裝在管道1上,然后再打開與管對齊的閥門繼續采樣;
⑤管道2的DNPH管采完樣后立即關閉管道2的閥門;
⑥管道1采完樣后立即關閉管道1的閥門,采完樣的捕集管應立即關閉兩端。
1.3 TENAX管、DNPH管的采樣條件
按照圖1所示安裝配管、TENAX管、DNPH管后,開始采集氣體。采集條件見表1。

表1 采集條件
在上述條件下,TENAX捕集管進行2次采樣。已捕集完的捕集管應立即進行分析。如不能立即進行分析,應用鋁箔包好捕集管后在陰涼黑暗處保管(10 ℃以下),保管期限最多為7天。
在上述條件下,DNPH管捕集管進行1次采樣。如不能立即進行分析,應用鋁箔包好捕集管后在陰涼黑暗處保管(10 ℃以下),保管期限最多為7天。
1.4 數據處理
揮發濃度按照下列公式計算:

式中:C為樣件揮發量,μg/m3;W為捕集管所測得化合物量,μg;Q0為按照25 ℃換算樣袋內所填充的純氮氣量,L。
2 結果分析
按照HJ/T 400-2007規定測定車內空氣有機物濃度[4],根據GB/T 27630《乘用車內空氣質量評價指南》,整車內空氣中有機物濃度要求見表2。
表2車內空氣中有機物濃度要求1 000 μg/m3
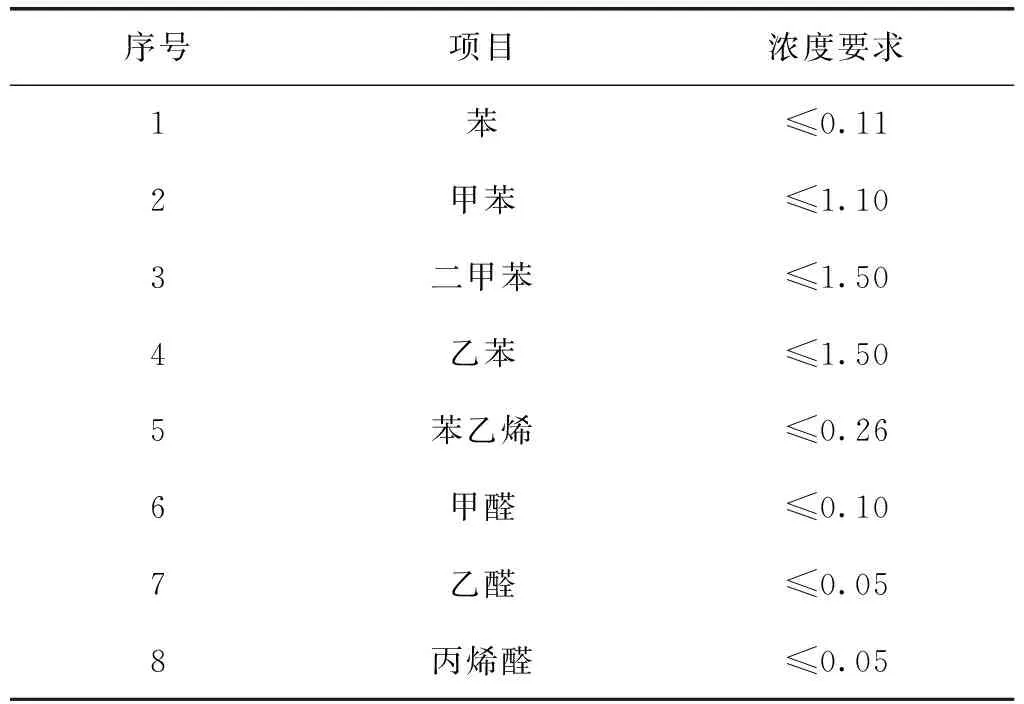
序號項目濃度要求1苯≤0.112甲苯≤1.103二甲苯≤1.504乙苯≤1.505苯乙烯≤0.266甲醛≤0.107乙醛≤0.058丙烯醛≤0.05
國家推薦標準中只對整車內部空氣有機物濃度提出了限值要求,而不是針對具體的零部件,各大主機廠對整車內部VOC的目標則是通過對零部件甚至是原材料和制造工藝的控制來實現的。整車內飾零部件材料類型如圖4所示。
整車內飾零部件所含有的揮發性有機物見表3。
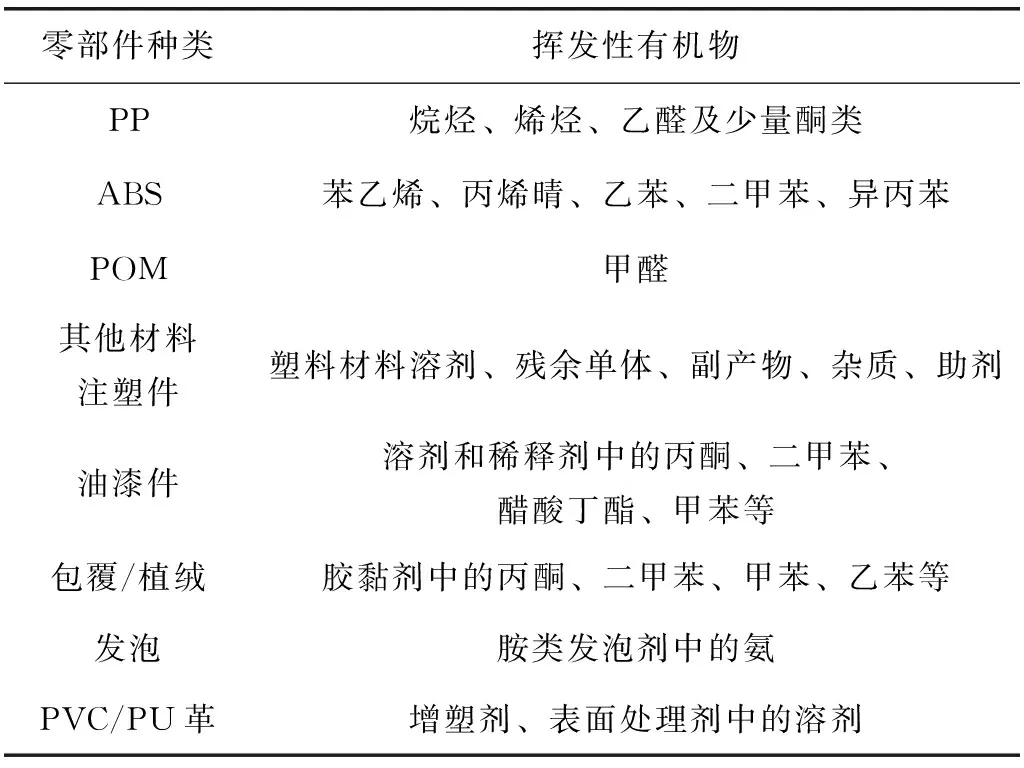
表3 內飾材料所含有的揮發性有機物
2.1 “對癥下藥”
一般通過控制零部件VOC有效實現整車內部空氣VOC濃度目標的方法為“對癥下藥”,具體實施手段是:先根據整車測試結果反饋超標物質鎖定需要整改的零部件,再通過控制此零部件的原材料及制造工藝來降低超標物質含量,進而有效實現整車內部空氣VOC濃度目標。
例如,某汽車主機廠檢測某新車型車內空氣VOC濃度,發現甲苯含量為2 300 μg/m3,根據表3,查詢對應的零部件種類可知影響整車內部空氣甲苯濃度的零部件可能有座椅面料、地毯、頂棚及遮陽板面料;通過對這幾種零部件VOC的檢測,找出甲苯濃度貢獻最大的一種或幾種零部件,如座椅面料貢獻的甲苯濃度為1 800 μg/m3,則通過對座椅面料的原材料進行檢測控制、對座椅制造過程中的溶劑助劑進行更換等方法來整改座椅,最終使整車車內空氣甲苯濃度在1 100 μg/m3以下。
此方法簡單有效,直接達到降低整車內部空氣VOC的效果,但是難以形成可依據的數據庫,無法快速找到源頭,當幾種零部件的貢獻度相當時,只能同時控制整改這幾種零部件,浪費資源,且會引起零部件廠商的抱怨。
2.2 零部件VOC的企業標準
經過不斷的探索,某些主機廠總結“對癥下藥”管控零部件VOC含量的經驗,建立起零部件VOC限值的企業標準,直接管控零部件以間接滿足國家推薦標準。
此企業標準的形成是通過對車型的多次檢測,逐一找出合格濃度的揮發性有機物,檢測此揮發性有機物合格濃度的車型上所有的內飾零部件,將多次檢測結果取平均值,形成數據庫,成為評價零部件VOC的依據。例如,對某主機廠的某車型及其內飾零部件進行多次抽檢,結果顯示車內空氣苯乙烯濃度滿足國家推薦標準,則將內飾零部件的多次檢測結果中苯乙烯濃度值取平均值。此主機廠的企業標準中所規定的零部件揮發性苯乙烯濃度限值如表4所示[5]。
表4某主機廠內飾零部件揮發性苯乙烯濃度限值μg/m3

阻尼板總成40隔音隔熱墊(包含吸音棉、頂棚隔熱墊)50側圍內飾板總成、注塑類衣帽架20方向盤總成70遮陽板總成40室內線束30車門內飾板60備胎蓋板40車門密封條、玻璃呢槽40衣帽架40儀表板、副儀表板100行李箱護面、行李箱地毯20防火墻隔音墊50空調主機總成40后座椅總成40地毯50頂棚30前座椅總成50
此方法需要經過多次反復的檢測形成可依據的數據庫,通過數據庫再對相關零部件進行管控,更加有效、直接,能夠快速找到引起某揮發性有機物濃度超標的零部件,同時也有了整改的目標。各大主機廠都在摸索零部件VOC的評價標準,此方法逐漸被廣泛地接受和使用。
3 總結
近年來,由車內空氣污染引發的糾紛和訴訟日漸增多,在零部件VOC的相關標準推出之前,各大主機廠都在極力地完善自己的檢測評價方法,以有效地控制車內空氣VOC濃度,有的主機廠通過建立評價數據庫,有的主機廠通過控制零部件的制造過程及工藝。
隨著汽車行業的迅猛發展和各種新材料的應用,具有低VOC的原料將充分應用在汽車零部件的制造中。如日之升推出低VOC聚丙烯復合材料,已成功用于安全帶護殼、耐刮擦門板上,且此材料具有優異的綜合性能,同時易于大型制件的成型加工,滿足汽車內飾件的力學性能及加工方面的要求。
【1】 王新,丁鐘.汽車車室內VOC探討及膠粘劑解決對策[J].化工新材料,2013,41(2):157-159,167.
【2】 環境保護部科技標準司.GB/T 27630 乘用車內空氣質量評價指南[S].北京:中國標準出版社,2011:1.
【3】 王亮,黃江玲,劉丹丹.汽車內飾零部件及其材料VOC含量分析的采樣方法[J].汽車工藝與材料,2012(12):12-17.
【4】 環境保護部科技標準司.HJ/T 400-2007 車內揮發性有機物和醛酮類物質采樣測定方法[S].2007:1-21.
【5】 陳林萍,王偉,曹維福.Q/JQ 11159車內零部件揮發性有機物要求及測試方法[S].合肥:江淮汽車股份有限公司,2012:3-9.
VOCTestofAutomotiveInteriorTrimPartsUsingSamplingBagsMethodandResultAnalysis
SUN Chengwu,CHEN Linping,CAO Weifu
(Jianghuai Automotive Co., Ltd., Hefei Anhui 230022, China)
2014-01-27
孫成武(1987—),男,工學碩士,工程師,從事汽車軟內飾材料結構設計。E-mail:ai041031@163.com。

