基于最小二乘支持向量機微陣列基因特征分類

高 振 斌

(西安財經大學統計學院數學與應用數學研究所 陜西 西安 710100)

0 引 言

隨著大規模基因表達譜技術的發展，人類各種組織的正常基因表達已經獲得，各類病人的基因表達譜都有了參考的基準，因此基因表達數據的分析與建模已經成為生物信息學研究領域中的重要課題。

眾多的研究者在此方向上進行了卓有成效的研究[1-4]。Chiaretti等[5]對T細胞急性白血病的基因表達譜的分類進行了研究，并應用到臨床治療和預測之中；Sun等[6]在肺癌臨床治療中通過對脫氧核糖核酸(DNA)微陣列數據特征分類從而作出預判；Devi等[7]基于互信息選擇信息基因，進而使用支持向量機(SVM)分類器對微陣列數據集進行分類評價；Wang等[8]采用改進的偏最小二乘遞歸式特征消除(PLS-RFE)算法對多個微陣列數據集進行特征分類和選擇，計算效率得到提高；Sharbaf等[9]先采用Fisher指標進行濾波，降低數據集維數，然后將元胞學習自動機(CLA)與蟻群算法(ACO)相結合，提高了基因特征分類精度;Khan等[10]提出了一種新的自適應徑向基核函數，并在非線性系統辨識、微陣列數據分類以及函數近似計算中做了仿真研究;Xiao等[11]提出一種基于多模型集成的深度學習算法，并對三種癌癥數據集進行驗證;李穎新等[12]研究了急性白血病的分類信息基因選取，并以SVM作為分類器進行亞型識別；馬煜等[13]將密度聚類與共享近鄰法相結合，對微陣列數據進行聚類分析;韓利等[14]將粗糙集與SVM結合，通過粗糙集進行基因特征約簡，然后用SVM進行數據分類；朱欽平等[15]提出了一種微陣列基因差異表達的多重假設檢驗方法，有效地減弱了數據噪聲帶來的假陽性結果;姚全珠等[16]研究了最小二乘支持向量機(LS-SVM)特征選擇時參數優化算法;孫剛等[17]采用改進的LASSO算法對信息基因進行特征選擇，剔除冗余基因；楊勤等[18]提出一種核最小二乘特征基因選擇方法，對微陣列數據進行降維，然后用極限學習機進行訓練和預測。

本文采用兩種典型的腫瘤微陣列數據集(結腸癌數據集、白血病數據集)，對數據進行歸一化處理，計算其相關系數矩陣；使用主成分分析(PCA)法進行降維；使用LS-SVM對降維后的特征信息基因進行分類，并與其他幾種分類方法進行了比較。

1 問題描述

假設微陣列特征分類問題可表示為集合O=(X,Y,F)，其中，X={x1,x2,…,xN}為樣本集，共有N個樣本；Y={y1,y2,…,yN}為信息標簽集；F={f1,f2,…,fN}為特征集；并且，xk∈X是一個包含m個元素(基因表達水平)的向量，可表示為xk=[x1k,x2k,…,xmk]T∈Rm;yk∈Y是與xk相對應的標量；假設為兩分類(ω1和ω2)問題，則有：

目的是尋找一組特征信息基因向量fk=[f1k,f2k,…,fpk]T∈F(p≤m)，使之能夠精確區分樣本的基因表達數據。假定所選的特征子集的數目p盡可能小。

2 SVM和LS-SVM

SVM是一種基于統計學習理論，采用結構風險最小化原理的機器學習算法，可以有效地處理高維樣本的分類問題，計算復雜度受樣本維數的影響較小，適合處理小樣本、高維數的基因表達數據的樣本分類問題。

SVM模型的目的是構造一個如下形式的最優分類函數：

f(x)=sgn[wTφ(x)+b]

(2)

式中：φ(x)為將輸入數據映射到高維特征空間的非線性映射；w為超平面權值系數向量；b為偏置項。標準支持向量機分類問題可描述為如下優化問題：

s.t.yk[wTφ(xk)+b]≥1-ek

ek≥0,k=1,2,…,N

式中：ek為誤差；w=[w1,w2,…,wN]T為權值系數向量；γ>0為懲罰系數，它控制對超出誤差樣本的懲罰程度。

LS-SVM算法是在SVM的基礎上通過最小二乘法利用誤差平方和選擇超平面，然后引進平方損失函數，將不等式約束轉換為線性等式條件，將二次規劃問題轉化為線性求解問題。LS-SVM分類問題可描述為求解下面的等式約束優化問題：

s.t.yk[wTφ(xk)+b]=1-ek

k=1,2,…,N

式中：e=[e1,e2,…,eN]T。

構造Lagrange函數如下：

b]-1+ek}

(5)

式中：αk≥0(k=1,2…,N)為Lagrange乘子。對上式進行優化，即求L對w、b、ek、αk的偏導數為零，經過化簡，可得到如下的線性方程組：

式中:

Z=[φ(x1)y1,φ(x2)y2,…,φ(xN)yN]T，

y=[y1,y2,…,yN]T，1N=[1,1,…,1]T，

α=[α1,α2,…,αN]T，I為單位矩陣。消除變量w、e，再利用Mercer條件:

Ωsl=ysylφT(xs)φ(xl)=ysylK(xs,xl)

s,l=1,2,…,N

(7)

可得矩陣方程：

式中：Ω=[Ωsl]N×N。假設A=Ω+γ-1I，由于A為對稱半正定矩陣，因而A-1存在，上式有解。得到LS-SVM分類器為：

f(x)=sgn[αkykK(x,xk)+b]k=1,2,…,N

(9)

式中：αk、b為式(8)的解。

取徑向基核函數為:

3 算法實現

3.1 數據預處理

通常，原始數據集在特征選擇之前應該被標準化。對于微陣列數據上一個基因中每個樣本的表達值，減去該基因所有樣本的平均值，再除以該基因所有樣本的標準差。經過標準化之后，一個基因在所有樣本上的表達值滿足均值為0，標準差為1的正態分布。

針對微陣列樣本集X={x1,x2,…,xN}，且xk=[x1k,x2k,…,xmk]T，數據歸一化計算如下：

式中：μi和σi分別是為第i個基因表達值的均值和標準差。

3.2 相關系數矩陣

對歸一化數據求相關系數為:

3.3 提取主成分分量

主成分分析法的基本思想是在保留盡可能多的原始信息的前提下達到降維的目的。

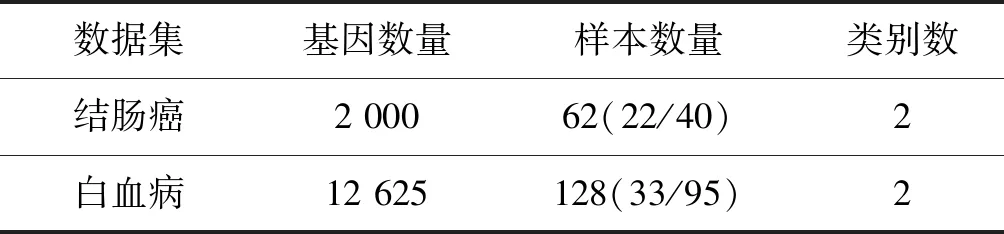
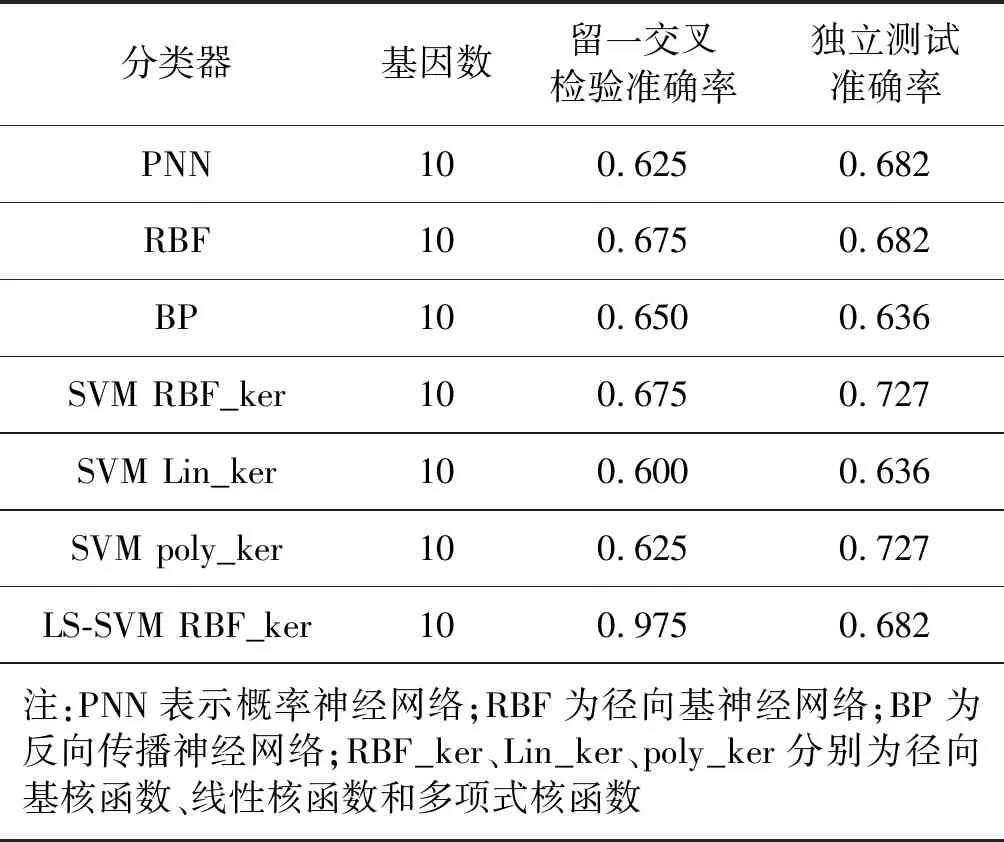
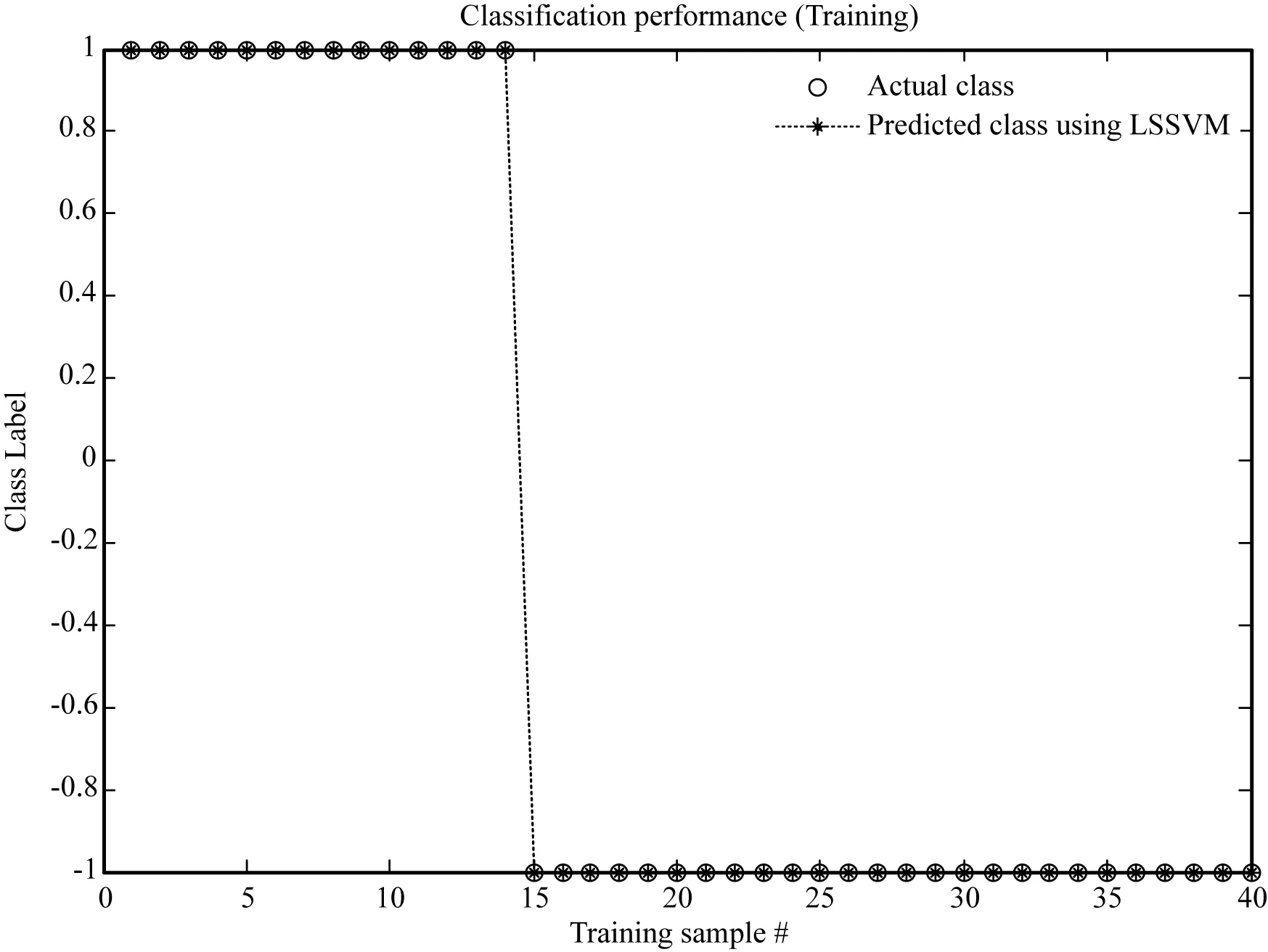
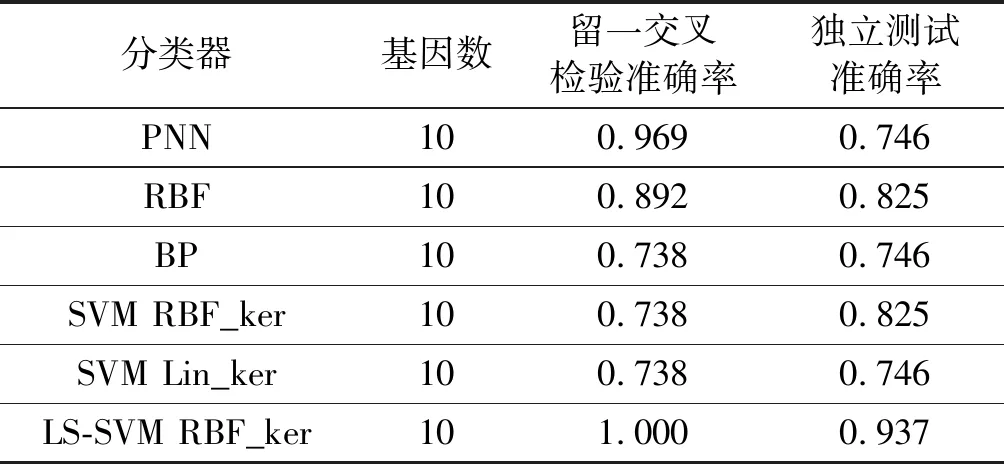
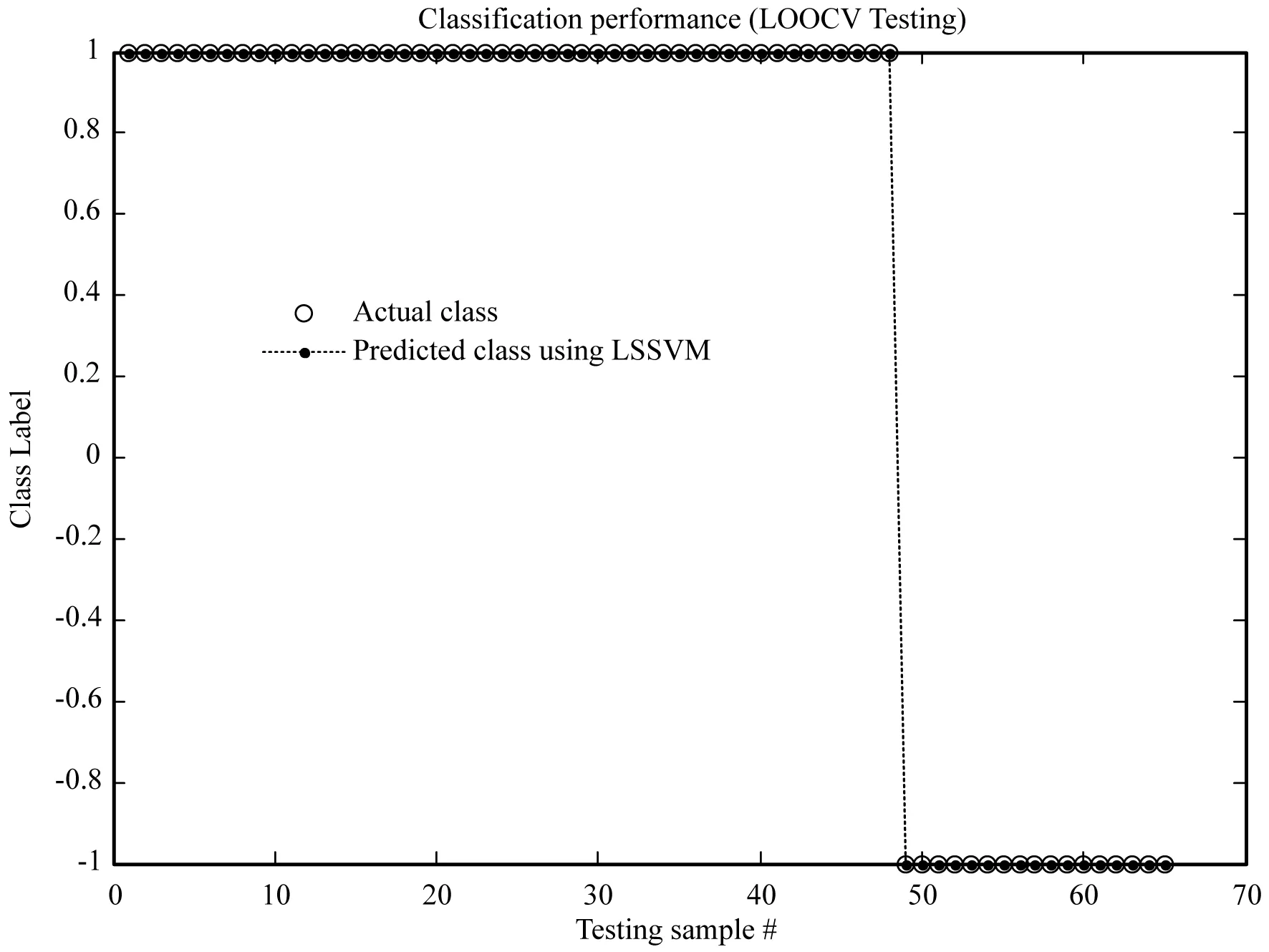
求解特征方程：|λI-R|=0，其中，R=[rij]∈Rm×m為相關系數矩陣；求出m個特征值λ1≥λ2≥…≥λm≥0。確定主成分數量p(

實現微陣列數據的降維和特征分類步驟如下：

Step1數據預處理。對微陣列數據集進行歸一化處理。

Step2提取主成分分量。計算相關系數矩陣；采用PCA法，對所選擇的基因樣本數據進行降維處理，得到樣本的特征信息基因集。

Step3分類模型訓練。對特征提取后的信息基因數據分別采用LS-SVM等分類器進行訓練，得到分類模型。

Step4測試分類模型。將測試樣本代入分類模型中，分別采用留一檢測法和獨立測試法評估各種分類器的性能。

4 仿真實驗

4.1 實驗數據及開發環境

實驗采用兩個公開的微陣列數據集來評估本文算法的性能。數據集的詳細描述見表1。結腸癌數據集包括62個樣本，且分成兩類：正常樣本和結腸癌樣本。其中，正常樣本22個，結腸癌樣本40個和2 000個基因[1]；白血病數據集包括128個樣本，分屬于兩類不同類型的腫瘤：T細胞ALL(共33例)樣本和B細胞ALL(共95例)樣本和12 625個基因[5,19]。

表1 實驗數據及描述

本文的實驗環境：Intel CPU 2.53 GHz處理器，2 GB內存的PC機，Windows XP操作系統，MATLAB 2014b開發環境。

4.2 實驗結果分析

實驗1結腸癌數據集分類

針對結腸癌數據集，實驗首先經過數據預處理，然后，將正常樣本和腫瘤樣本按接近2∶1的比例隨機地分配到訓練集和測試集中。訓練集有40個樣本(其中正常樣本14，腫瘤樣本26)，測試集有22個樣本(正常樣本8個，腫瘤樣本14個)。

然后通過PCA降維方法，提取主成分前十的特征信息基因如表2所示。

表2 結腸癌數據集中選取的特征基因

分別采用LS-SVM等分類器對選取的特征基因進行分類。各分類器分類準確率結果見表3。圖1、圖2為LS-SVM分類器訓練模型準確率(100%)以及獨立測試實驗準確率(68.18%)結果圖。

表3 結腸癌數據集選取的特征基因集實驗結果

圖1 結腸癌數據LS-SVM訓練模型準確率

圖2 結腸癌數據LS-SVM獨立測試準確率

實驗2白血病數據集分類

白血病數據集經過數據預處理，由PCA法求得主成分前十的特征信息基因如表4所示。

表4 白血病數據集中選取的特征基因

將數據集中的兩類樣本分配到訓練集和測試集中。訓練集有65個樣本(T細胞樣本有48個，B細胞樣本有17個)，測試集有63個樣本(T細胞樣本有47個，B細胞樣本有16個)。

對選取的特征基因進行分類，分別采用留一交叉檢驗和獨立測試實驗，結果見表5。圖3、圖4分別為LSSVM分類器留一交叉檢驗準確率(100%)和獨立測試實驗準確率(93.65%)結果圖。

表5 白血病數據集選取的特征基因集實驗結果

圖3 白血病數據LS-SVM留一交叉檢驗測試準確率

圖4 白血病數據集LS-SVM獨立測試準確率

從表3、表5中看出，對于兩個數據集的留一交叉檢驗結果，LS-SVM分類器的準確率最高，分別為97.5%和100%，其次是PNN分類器和RBF分類器；獨立測試實驗結果中，白血病特征基因集的LS-SVM分類器的準確率最高，為93.65%，而結腸癌數據集LS-SVM分類結果與其他分類器的結果差別不大。

5 結 語

微陣列數據對疾病的診斷有很重要的參考價值，但是，微陣列數據的高維和高冗余給進一步挖掘其中蘊含的知識帶來極大困難，其中一個關鍵任務就是信息基因的選擇。LS-SVM分類器將SVM優化問題的不等式約束轉換為線性等式條件，將二次規劃問題轉化為線性求解問題，避免了求解耗時，提高了運行效率。本文基于LS-SVM分類器對兩類癌癥微陣列數據集的基因分別進行提取和分類。首先，對微陣列數據進行歸一化預處理，計算其相關系數矩陣，并運用PCA法進行降維。提取特征信息基因集(各取10個基因)，運用不同的分類器(包括LS-SVM、PNN、RBF、BP及SVM)進行分類。從留一交叉檢驗和獨立測試兩種實驗結果可以看出，運用LS-SVM分類器，結腸癌集準確率分別達到97.5%和68.2%；白血病集準確率分別達到100%和93.7%，從而證明了本文提出的算法比運用其他分類器計算準確率相對較高，能夠為醫學臨床實踐提供較為可靠的判斷依據。