高考試題中函數零點問題的解題策略
李 偉
(遼寧省鞍山市第三中學 114012)
函數的零點是高中數學重要概念之一,也是近幾年高考命題的熱點,所以,很有必要針對函數零點問題做一梳理和總結.下面是按解決函數零點問題的方法和手段進行分類,概括性地給出高考試題中函數零點問題的解題策略.
一、解方程法
分析函數f(x)零點的概念就是方程f(x)=0的解,所以,最基本的求零點的方法實質上就是解方程.本題的解決就是基于這樣的思考.
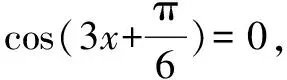
點評函數零點是通過方程的根來定義的,所以解方程求根是解決函數零點問題的基本方法.但當面對有些不可解的方程時,需要通過觀察法等手段尋找方程的根,這是需要解決零點問題要注意到的事情,特別是對于超越方程尋求其解時顯得更重要.
二、數形結合法
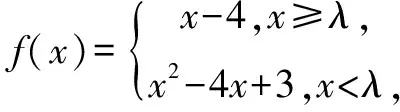
分析第一個空略.
對于第二個空,函數f(x)零點的概念就是方程f(x)=0的解,也可以表述為函數y=f(x)的圖象與x軸交點的橫坐標.由于函數f(x)是分段函數,我們可采取分別在兩個直角坐標系中作出f(x)=x-4,x≥λ,f(x)=x2-4x+3,x<λ的圖象.
通過函數圖象和題中條件要求對比,即可得到結論.
略解在同一坐標系中分別作出函數f(x)=x-4,x≥λ,f(x)=x2-4x+3,x<λ. 由圖象對比可知:1<λ≤3或λ>4.
點評數形結合是高中數學中最重要的解題思想方法之一.利用數形結合解決問題關鍵變式構造函數,其核心是通過變式的目的是為構造函數打下伏筆,構造函數式為把復雜問題、不便于畫圖形的問題簡單化.利用數形結合解決問題另一關鍵之處是要有運動變化的思想,在圖象相對位置、不同情況充分考慮到,不留漏洞,這樣能確保問題順利解決.
三、奇偶函數性質法
(2018年全國2卷,理11)已知f(x)是定義域為R的奇函數,滿足f(1-x)=f(x+1).若f(1)=2,則f(1)+f(2)+f(3)+…+f(50)的值為( ).
A.-50 B.0 C.2 D.50
分析f(x)是定義域為R的奇函數,所以x=0是f(x)的一個零點.又借助枚舉法得到f(x)是以4為周期的周期函數,且在一個周期內其函數值的和為0.整合上述結論可得答案.
略解因為f(x)是定義域為R的奇函數,所以x=0是f(x)的一個零點.即f(0)=0 .
又注意到f(1-x)=f(x+1),f(1)=2,所以f(2)=f(0)=0,f(3)=f(-1)=-f(1)=-2,f(4)=f(-2)=-f(2)=0,f(5)=f(-3)=-f(3)=2,f(6)=f(-4)=-f(4)=0,f(7)=f(-5)=-f(5)=-2,…,所以f(x)是周期為4的周期函數,且一個周期內函數值的和為0.
又f(49)=f(48+1)=f(1)=2,f(50)=f(48+2)=f(2)=0,所以選C.
點評具有奇(偶)性的函數有著關于原點(y軸)對稱的性質,這樣既可以幫助找到特殊零點,也可把問題轉化到x軸的半軸上解決.周期性的作用在于把自變量取值范圍簡化到在一個周期內問題得到解決,則自變量取值范圍的問題即可全部得到解決.在此要強調的是借助“點、軸對稱”、“軸、軸對稱”確定函數周期性的小結論是要掌握的.
四、單調函數法
(2016年江蘇卷,19)已知f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
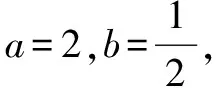
①求方程f(x)=2的根;
②若對于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求實數m的最大值;
(2)若0
分析(1)略.
對于問題(2)解決,條件是g(x)=f(x)-2有且只有1個零點,結論是求ab的值.是已知零點求參數問題.注意到:函數g(x)=f(x)-2有且只有1個零點等價于函數g(x)具有單調性,并且g(x)=0有一根.所以,問題的解決分為兩步進行,一是考察單調性,二是零點存在.
略解(1)略.

點評由函數的單調性來研究函數的零點,主要針對零點唯一.題型為:一類是直接判斷函數式結構特點直接判斷單調性;一類是借助導數來判斷單調性.要注意的是單調函數未必有零點(如:y=2x是增函數,但沒有零點),所以,用單調性判斷零點存在性,還要附加:存在實數a、b,使得f(a)f(b)<0.
五、極(最)值法
(2017年全國理科一卷,21)已知函數f(x)=ae2x+(a-2)ex-x.
(1)討論f(x)的單調性;
(2)若f(x)有兩個零點,求a的取值范圍.
分析(1)略.
對于問題(2),條件中函數f(x)有兩個零點等價于函數y=f(x)圖象與x軸有兩個交點;這樣問題就轉化為函數y=f(x)極小值小(大)于零,且在取得極小值的之變量值兩側存在a、b,使得f(a)>0,同時f(b)>0(或小于零).
略解(1)略.
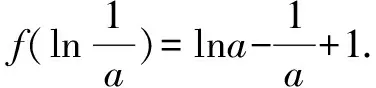
點評函數有兩個(甚至更多)零點問題,從數形結合角度看,是觀察圖象與x軸的交點個數;從代數角度看,可從極值的正負角度來分析.這樣就把零點問題,轉化為研究函數極值問題.
以上是就近幾年高考試題中關于零點問題解題策略的提煉與概括,就試題而言,還有很多題目,在此不可能,也沒有必要逐一列舉.縱觀函數零點問題可分為求零點、判斷零點和已知零點存在否求參數問題,對于這三種題型,上述問題中都有所體現.可以說,如果對于零點問題我們能認識到如此程度,高考中的零點問題必然迎刃而解.

