從一道導數壓軸試題談導數復習
蘇藝偉
(福建省龍海第一中學新校區 363100)
一、試題
(2016年全國Ⅱ卷理科第21題)
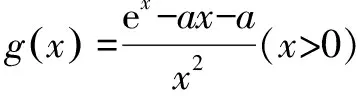
二、試題評析
本題以函數為背景,融合了函數,導數,不等式,最值問題于一體,重點考查用導數研究函數的單調性,極值,零點,值域等問題,突出對學生的數學運算,數學抽象,邏輯推理等能力的考查.本題分為兩小題,在難度上逐次遞增,有梯度性;在解題思路上,第(1)問考查函數f(x)的單調性以及不等式的證明,借助導數工具可順利求解.第(2)問要求的是函數g(x)的最小值h(a)的值域,需借助函數求值域的方法求解,即將h(a)表示成某個變量(這個變量可能是a,也可能是隱零點x0)的一元函數模型.兩小題表面上看似無關,其實第(1)問為第(2)問的求解做了鋪墊,第(2)問的求解需要借助第(1)問的相關結論,考生要將兩問聯系起來方能正確求解.
三、試題解析
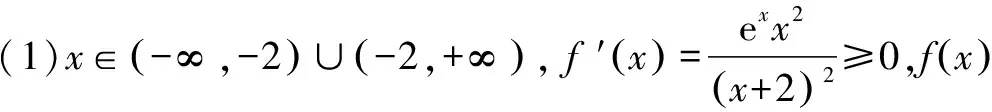
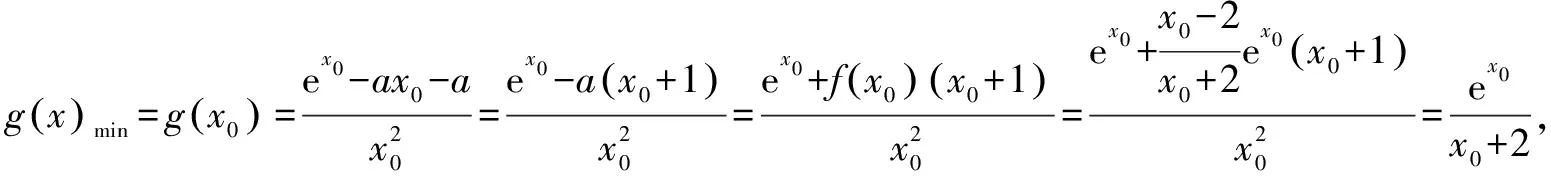
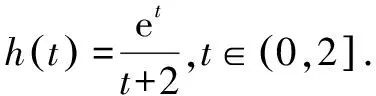

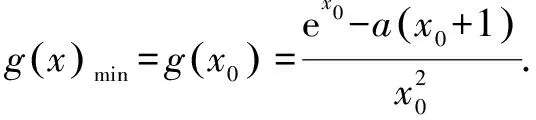
四、試題變式
(1)求函數f(x)=xlnx+a(a<0)的零點個數.
(2)證明:當a∈[-4e,0)時,函數g(x)=2x2lnx-x2+ax有最小值.設g(x)的最小值為h(a),求函數h(a)的值域.
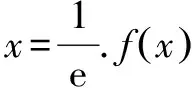
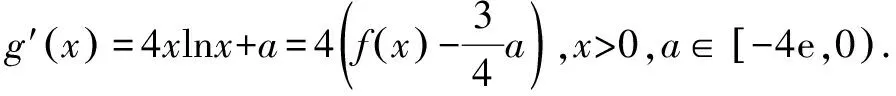
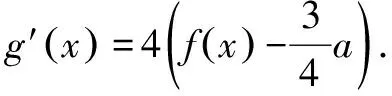
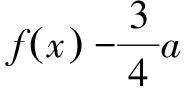
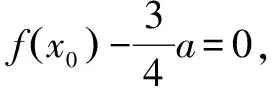
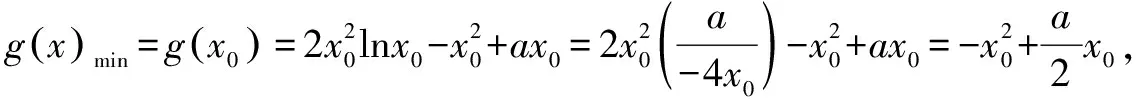
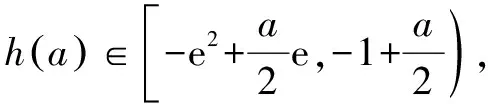
五、教學啟示
第一:加強導數運算,提高數學運算素養.
數學運算是數學的核心素養之一,數學離不開運算.導數問題中,準確求導是解決問題的基礎,正確運算是解答問題的關鍵,所以在復習中一定要牢固掌握基礎知識,基本技能,基本方法.因此,在復習導數問題時,讓學生真正掌握導數的概念,導數的幾何意義,導數的運算法則,熟練運用導數求函數的極值,最值,單調性,零點,切線方程,對這些內容要進行分塊講解,逐一復習,牢固掌握基礎知識,才能保證數學運算的準確性.
第二:講透通性通法,提升邏輯推理素養.
高考對函數和導數的考查側重于理解和應用,試題有一定的綜合性,并與數學思想方法緊密結合,對函數與方程思想,數形結合思想,分類討論思想都進行深入考查,體現能力立意的命題原則.基于此,在復習中要以典型試題(如全國卷試題)為例,講透解決某一類題型的通性通法,進而讓學生在掌握通性通法的基礎上變式運用,從而提升學生的邏輯推理能力,提升數學核心素養.

