高三復習中“一類函數的最值”問題的探索與思考
2019-08-14 07:22:20張先宏
數理化解題研究 2019年19期
關鍵詞:方法
張先宏
(安徽省含山中學 238100)
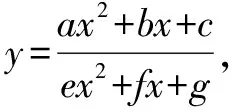
一、分式函數的探索
本文介紹的分式函數在高考中常考,其分子和分母均由函數式構成,且函數結構隨著a、b、c、e、f、g取值的變化而變化.當a、e為零時,函數變成“一元一次分式函數”,求解難度降低;當a、e不全為零時,函數結構為“一元二次分式函數”,求解難度增加.不僅如此,常數的改變會引起函數結構的改變,都會影響求解難度,同時,由于分母不能為零,函數的定義域對最值也會有影響.求解此類函數時應密切注意分子與分母的關系,以求最簡易的解題方法.
二、分式函數多種題型的解析
1.當a、e為零時
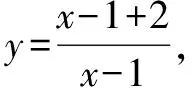
2.當a、e不全為零時
此時,函數變為“一元二次分式函數”,這類函數最值求解難度大,且情況多,更復雜,下面進行分類討論:
(1)當函數可以進行分母分子約分時
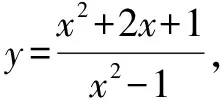
(2)當函數分子分母不能進行約分時
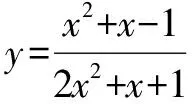
這道函數題不能約分簡化,怎么辦呢?易知分母不可能為零,x的取值范圍為R,可以對函數化整變形得到:(2y-1)x2+(y-1)x+y+1=0.
顯然,2y-1≠0時函數式變成了關于x的一元二次方程,因為原函數中x的取值范圍為R,所以方程一定有實根,這時,我們應該想到方程有實根的判定方法,即判別式大于等于0,此題中即:(y-1)2-4(2y-1)(y+1)≥0,解不等式,就能得到函數最值,這里不進行求解.
(3)當x的取值范圍受到區間限制時
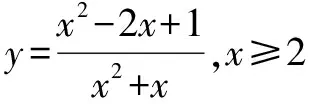
3.均值不等式法求解
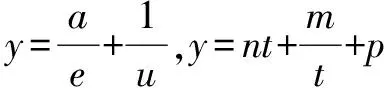
本文對人教版數學高三復習一類分式函數的最值求解進行了分析探討,介紹了分式函數的各種形式以及不同的解答方法,其解答方法多種多樣,加上其各系數的改變也會影響解答方法的選擇.所以,學生需要努力掌握每種方法,不僅要會做題,更要理解其本質,掌握各區塊的知識點,在高考時碰到類似題型才能迎刃而解,從而在高考數學中取得自己滿意的成績,為自己未來的人生打下良好的基礎.
猜你喜歡
中老年保健(2021年9期)2021-08-24 03:52:04
河北畫報(2021年2期)2021-05-25 02:07:46
中學生數理化(高中版.高考理化)(2020年2期)2020-04-21 05:33:04
兒童繪本(2020年5期)2020-04-07 17:46:30
兒童故事畫報(2019年5期)2019-05-26 14:26:14
Coco薇(2016年2期)2016-03-22 02:42:52
山東青年(2016年1期)2016-02-28 14:25:23
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

