高中物理教學中數理結合理論研究

周滿意

(甘肅省靜寧縣仁大中學 743411)

數理結合理論簡單來講就是數學思想與數學方法在物理教學中的應用，數學與物理兩門學科在長時間的發展中表明數學不僅僅是幫助學生學習物理知識的一種工具，同時也是物理學科中一些概念與原理的重要思想來源.

一、高中物理教學中數理結合理論概述

高中物理中的數理結合理論將其按照水平的不同可以分為表達式、函數與方程組式、測量與估算式、數學建模式以及圖形與圖像式等五個層次.數學與物理之間的關系又是個別與一般、特殊與具體之間的關系.數學作為一門極具抽象性的學科，其中完全沒有具體的現象，而物理作為一門以客觀物質本質為研究對象的學科、以物理實驗為基礎的自然學科，兩者在一定程度上具有很好的互補作用.因此，在高中階段的物理教學活動中將數學知識應用其中可以起到事半功倍的效果，同時在實際的應用中也應該注意以客觀事實為依據并受到物理規律的制約.教師在應用數學知識來幫助學生理解物理概念、應用物理原理、總結物理規律、解答物理問題時，也應該注意數學知識使用的局限性與特殊性.

二、數理結合在高中物理教學中的實際應用

1.數學模型在解決物理力學問題中的具體應用

題目如圖1所示，物體以一定的初速度沖上固定的光滑斜面，到達斜面最高點C時速度恰為零.經過時間t，物體運動到斜面3/4處的B點，求物體由B運動到C所用的時間.

解法2建立連續相等時間內的位移比例(數列)模型根據初速度為零勻加速直線運動的特點，建立比例模型，連續相等的時間內通過的位移之比為X1∶X2∶X3∶…Xn=1∶3∶5∶…∶(2n-1)，題中XCB∶XBA=XAC/4∶3XAC/4=1∶3 ，通過xAB段位移的時間為t，因此通過xBC時間為tBC=t.

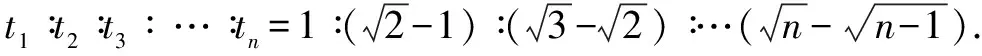
2.數學方法在高中物理中的具體應用

本小節所講到的數學方法主要是指函數換元在高中物理中的應用，在高中物理中的一些計算題中由于運算量較大、運算較為復雜，這時函數換元在其中的應用就顯得尤為重要.數學函數換元方法在高中物理解題中的應用可以將復雜的計算變得較為簡單，再加上實際的出題人主要考察的就是在該物理問題中學生對于函數換元方法掌握的熟練程度，他們會巧妙的設置該方法的應用角度，這就使得該數學方法在高中物理中變為更為重要.基于此，學生應該在教師的指導下在解答物理問題時注意該方法在其中的應用并學會靈活使用.例如，教師在講解這類物理問題時，處于不同兩地的兩個同學如果相向而行，這時可以將學生的運動看做是勻速直線運動，甲同學比已同學的出發時間晚了三分鐘，但是在兩位同學的相遇的地方確是甲同學比乙同學多走了三百米.如果從兩位同學相遇的時間點開始計算，乙同學在十分鐘之后、甲同學在一分鐘之后可以到達兩位同學彼此開始出發的地點.現問兩同學出發地點之間的實際距離是多少？對于這類物理問題的解決可以將函數換元的思想應用其中，以縮短解題時間，同時對于該類問題的解答也可以在很大程度上減少運算量.

總而言之，在高中物理教學中數學結合思想在其中發揮著非常主要的作用，數理結合理論也是高中物理教學中一個覆蓋面較廣且有深度的話題.以上主要內容是圍繞數理結合在高中物理教學中的具體應用展開論述的，通過在實際的教學中積極探索、認真總結、善于發現，來將數理結合理論在高中物理教學中的積極作用充分發揮出來，以提高學生在高中階段物理學習的良好效果.