拖曳系統回轉運動中的沖擊特性

王志博

(江蘇科技大學，張家港 215600)

0 引 言

拖曳系統的振動傳遞不僅危害到拖曳纜的安全性，也對拖曳系統的運動穩定性能產生影響，由于拖曳系統在直航拖曳過程中是低阻尼和高剛度的系統，如Niedzwecki[1]的模擬結果所示，拖曳纜在規則波中運動形成的張力歷程也服從規則的正余弦分布規律。但是在母船進行水平面操縱運動時，由于水流阻力沿著拖曳纜發生了變化，造成拖曳體沉深變化和沖擊等現象，Ablow[2]模擬了較短拖曳纜回轉運動中的拖曳體沉深歷程，Huang[3]基于凝集參數法模擬了拖曳系統的全回轉運動，具體的運動規律是拖曳系統完成回轉運動的過程中，存在拖曳纜的大范圍失速和跌落，造成了拖曳體的沉深陡增，尤其是回轉半徑較小的情況下，拖曳體的沉深顯著增大，其中也包含了部分非線性響應行為。Zhu[4]模擬了母船完成指定的水面操縱運動軌跡情況下拖曳體的運動和張力歷程，但是基于有限元的數值模型中采用了瑞利阻尼模型，這與水面操縱運動中的響應纜段部分失速造成的阻尼力差異較大。王志博[5]利用質量、剛度、阻尼的歸納方法建立動力學模型模擬了拖曳體在規則波中的運動響應。Wang[6]采用Ablow[2]的動力學模型模擬了母船水平面操縱參數對水下拖曳體的影響。由于Ablow 方法將纜的運動受力高度耦合，不用給出基于經驗的瑞利模型的參數，對拖曳系統進入回轉運動后拖曳系統的響應計算更為準確。然而引起從沖擊效應的結構出發建立模型，王志博[7]模擬了拖曳系統受強迫振動沖擊作用。Huang[8]，Chiou[9]和Driscoll[10]應用凝集參數法模擬了不同波浪運動狀態下的沖擊張力。Huang等[11]著重分析了拖曳纜受到的沖擊對拖曳體運動穩定性的影響，但是上述研究基于長響應周期，缺乏瞬態沖擊的效應描述。

本研究分析對瞬態沖擊效應，通過應用改進的自適應數值模擬技術，模擬在短時內發生的回轉沖擊現象。由于纜的沖擊張力現象和拖曳體的空間運動密不可分，本研究將拖曳體的空間運動與母船端的張力歷程結合分析，對拖曳體沉深和側向位移的變化與纜內張力的變化過程結合在一起進行分析。

1 動力學模型

拖曳纜的放纜長度大纜的彎曲和扭轉作用隨著纜長的增大而逐漸變得微弱，本文將纜簡化為柔性圓形橫截面質量均勻分布的纜，在纜上任意截取微元ds，在纜元的切線方向、法線方向和副法線方向，按照右手法則建立當地坐標系O-tnb，在當地坐標系下纜受到水流阻力、水中重量（重力和浮力的差）、附加質量力、纜內張力的作用，依據牛頓第二定律Ablow 對纜元受力建立了動力學模型，進而建立固定聯結在大地的坐標系O-XYZ，應用歐拉轉換關系可將當地坐標系轉換到全局坐標系中。

任意纜元處Ablow 推導的動力學方程控制方程可寫成：

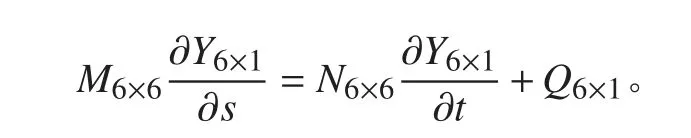
轉換到全局坐標系O-XYZ 中，系數矩陣M 的非零元素包括：

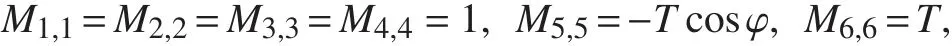
非對角線的非零系數為：

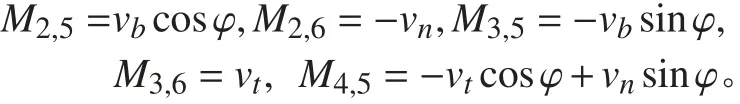
時間相關系數矩陣的非零變量為：

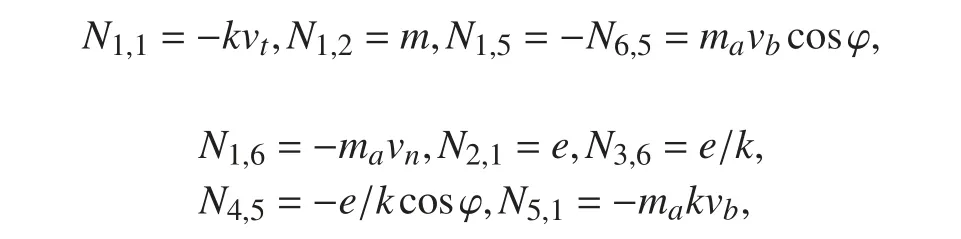
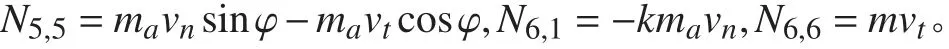
源項為纜元受到的水流阻力、水中重力和海流作用力分別寫成：

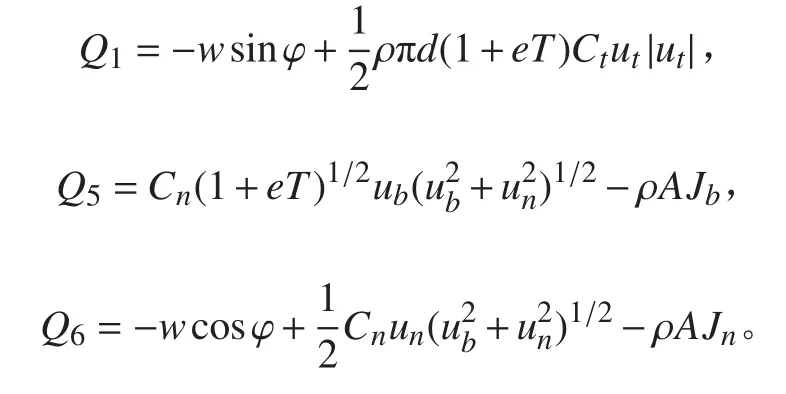
未知變量為纜內張力T、纜的運動速度相位角 ：

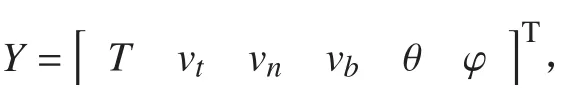
根據牛頓第二定律將拖曳體簡化成為質點運動寫成：

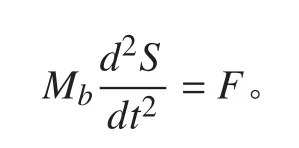
質量系數矩陣寫成：

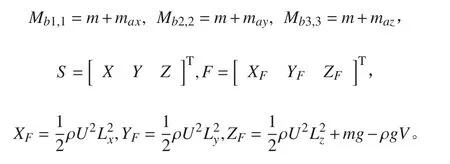
本研究以Burgess 推導的盒式格式為基礎，在每一個時間步長內增加松弛因子，在時間步長內多次迭代計算滿足求解精度要求，求解離散方程。

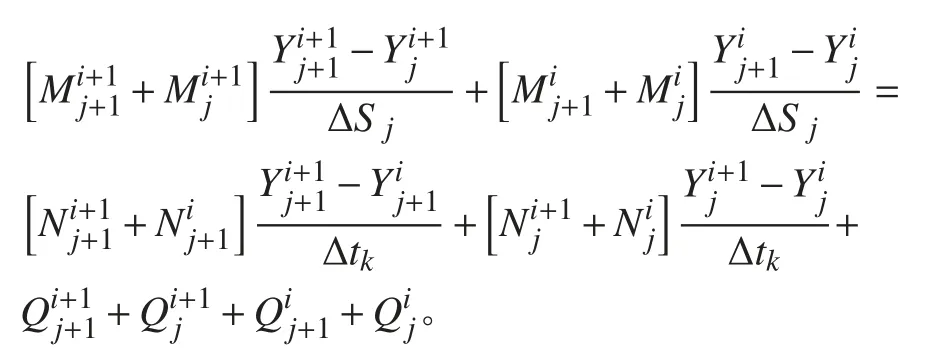
在拖曳纜受到外界擾動作用下，觀察結構矩陣M 可知，拖曳系統內的張力隨時間發生大幅度的振蕩導致該結構矩陣M 的性質發生了變化，從而造成數值求解的困難。為了克服每個時間步長內的張力求解值差別大，造成數值求解不穩定問題，采用自適應時間步長的方法求解上述盒式差分格式。首先取時間步長為某一個初始時間步長，如令k=1 進行計算。

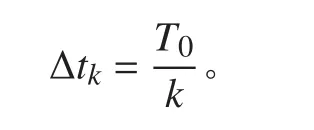
即可認為達到了對振動響應的時間分辨率。

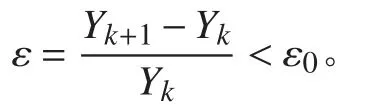
本文利用表1 所示的Huang 給出的算例進行驗證，在該拖曳系統基礎上擴展進行加速運動的振動響應計算。拖曳纜水下端在O-XY 水平面的運動軌跡和水深Z 向的升沉歷程計算結果對比如圖1 所示。通過比較可知，拖曳體的升沉運動與水平面內的運動軌跡基本一致，驗證了本模型對應程序的正確性。

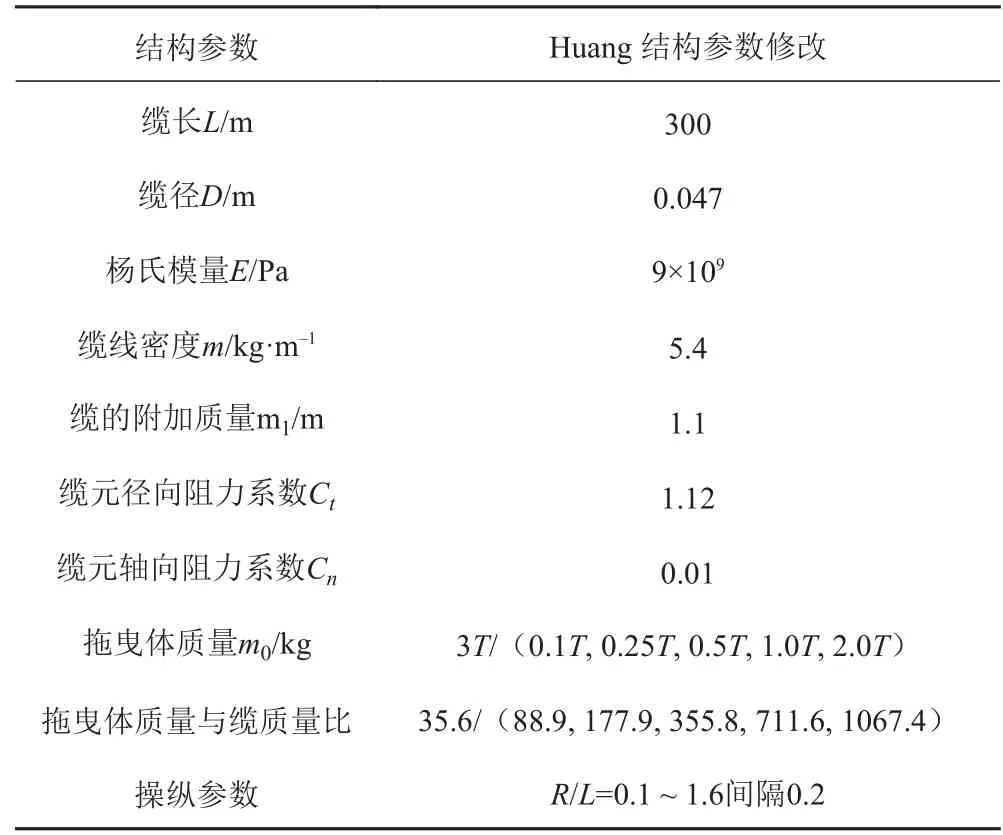
表 1 拖曳系統結構參數與操縱參數（纜的總質量和拖曳體的質量比）Tab. 1 Structural and maneuverable parameters of towed cable system

2 回轉運動驗證

在回轉運動中歷經了2 個張力振蕩的沖擊階段，一是拖曳系統進入回轉運動的過程中，拖曳纜內的張力振蕩，另一個是拖曳系統完全回轉運動后，進入直航拖曳狀態時，拖曳纜內的張力振蕩。

拖曳體在回轉過程中的運動基本規律如圖1 所示，拖曳系統進入回轉運動的過程中，拖曳體的回轉圈直徑要小于母船的回轉圈直徑，也就是拖曳體在母船的內側，那么纜運動的線速度下降，必然造成拖曳體沉深增大。同時拖曳體的沉深增大，直到回轉運動結束后，拖曳體才緩慢回復到之前的沉深，由于纜的空間運動和纜內張力高度耦合，纜受到的水流阻力減小產生失速效應，那么拖曳纜內的張力必然是先增大后減小。

如圖2 所示，由于進入回轉狀態下，拖曳纜的運動速度下降，纜受到的水流作用力陡降，拖曳纜內的張力產生振蕩，隨著纜運動速度下降，纜內的張力逐步增大，這稱為纜的失速效應。失速效應對應的沖擊階段成為第1 沖擊階段；在完成回轉運動后，拖曳系統又進入直航狀態，纜在獲得水流作用力的同時產生了沖擊作用，此階段的沖擊效應成為第2 沖擊階段。顯然第2 階段的沖擊效應要顯著大于第1 階段。也就是失速沖擊效低于加速沖擊效應。

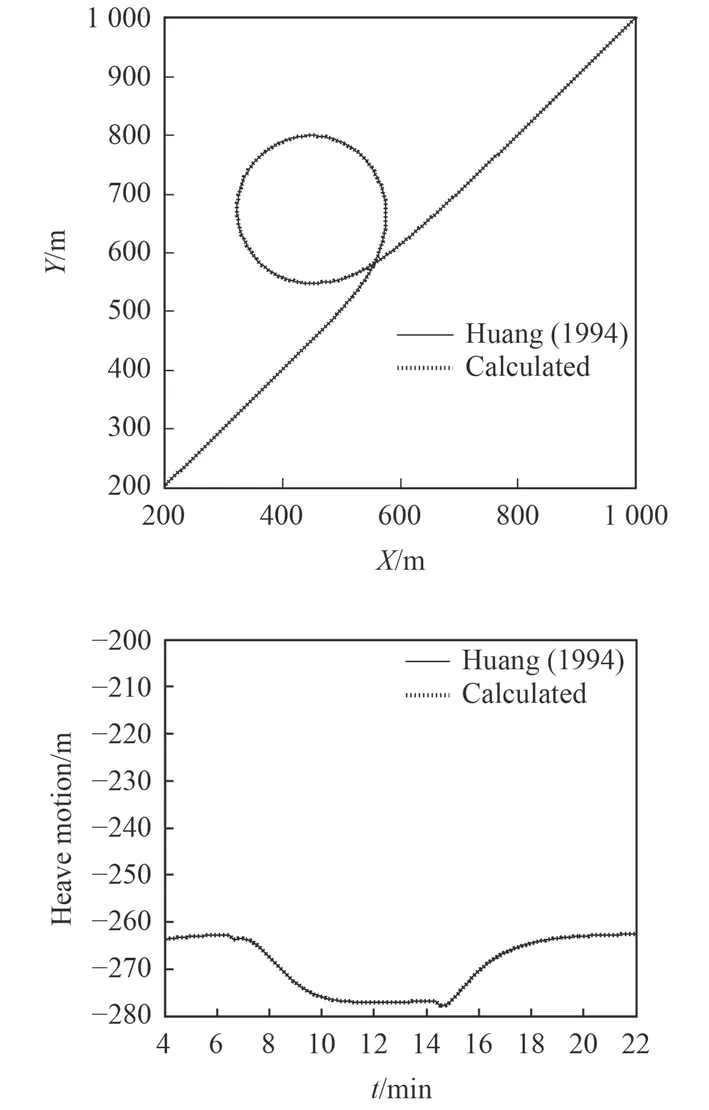
圖 1 拖曳體水下端回轉軌跡和升沉歷程的數值計算結果與Huang（1994）的計算結果的對比Fig. 1 Validation of numerical model with Huang (1994) by simulating turning path of towed system

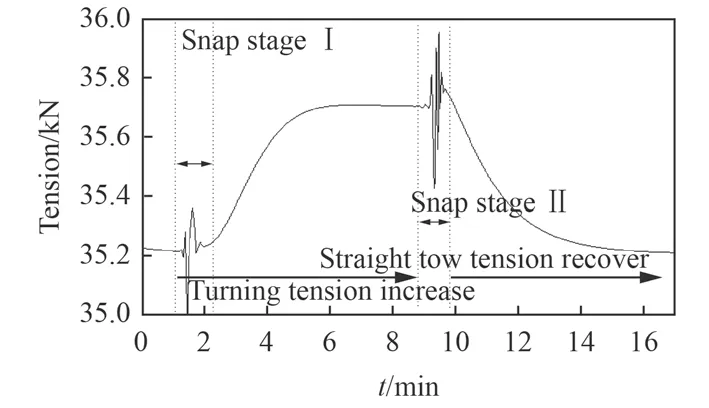
圖 2 回轉過程中拖曳纜水面端的張拉力時間歷程Fig. 2 Tension history in cable surface end during full turns

3 回轉運動中的拖曳纜受到的沖擊規律

以上驗證算例是在較大的回轉直徑情況下拖曳體形成了完整的回轉圈，本研究考查在較小回轉圈下存在沖擊現象。仍然以Huang 給出的驗證算例為基礎，通過修改拖曳系統的操縱參數和拖曳體的質量，分析拖曳系統在回轉運動過程中形成的沖擊張力隨著設計參數的變化規律。修改拖曳系統的操縱參數和結構參數包括回轉圈的直徑、回轉速度、拖曳體的重量。

3.1 同一回轉半徑不同回轉速度時的沖擊規律

圖3 為回轉運動的水平運動軌跡，圖4 為拖曳體的升沉歷程。隨著拖曳速度的提升，拖曳體向回轉圈內側的側向位移逐漸增加，拖曳體的側向移動增大。隨著拖曳速度的增大拖曳體的下潛段將在更短的時間內完成，這需要水流作用力在較短的時間內使拖曳體恢復到原先的潛深，拖曳速度越大，拖曳體的潛深變化越大而完成沉深恢復的時間卻縮短了，如圖5 所示存在2 個沖擊階段，拖曳纜內必然形成較大的沖擊峰值。然而沖擊持續的時間卻沒有顯著增大，這是由于快速進入直航拖曳后拖曳體的運動將趨于穩定。

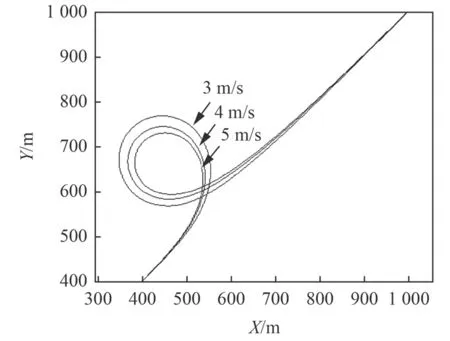
圖 3 不同拖曳速度下的拖曳體水平回轉軌跡Fig. 3 Horizontal trajectory of towed body in differenttowed velocity

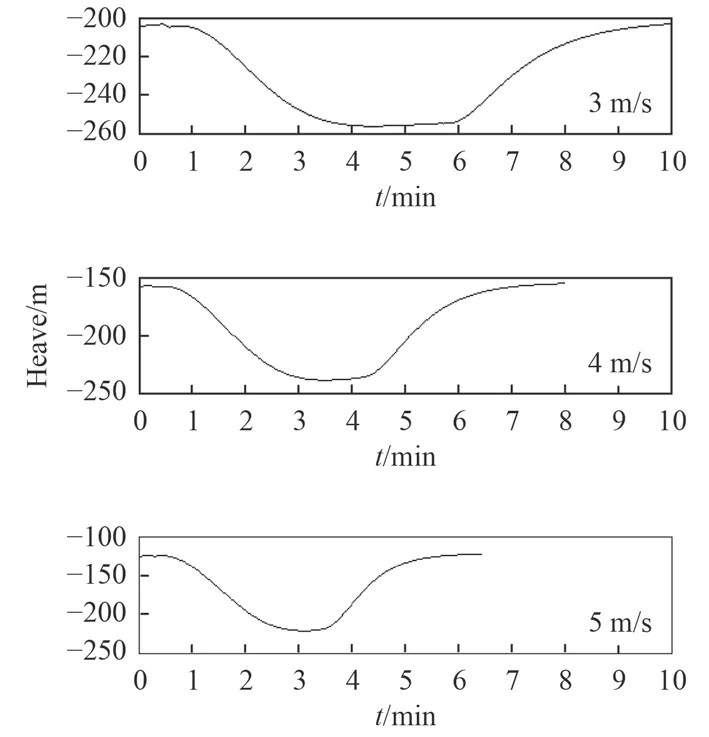
圖 4 不同拖曳速度對應的拖曳體升沉歷程Fig. 4 Heaving history of towed body in different towed velocity

3.2 同一拖曳速度不同回轉半徑下沖擊規律

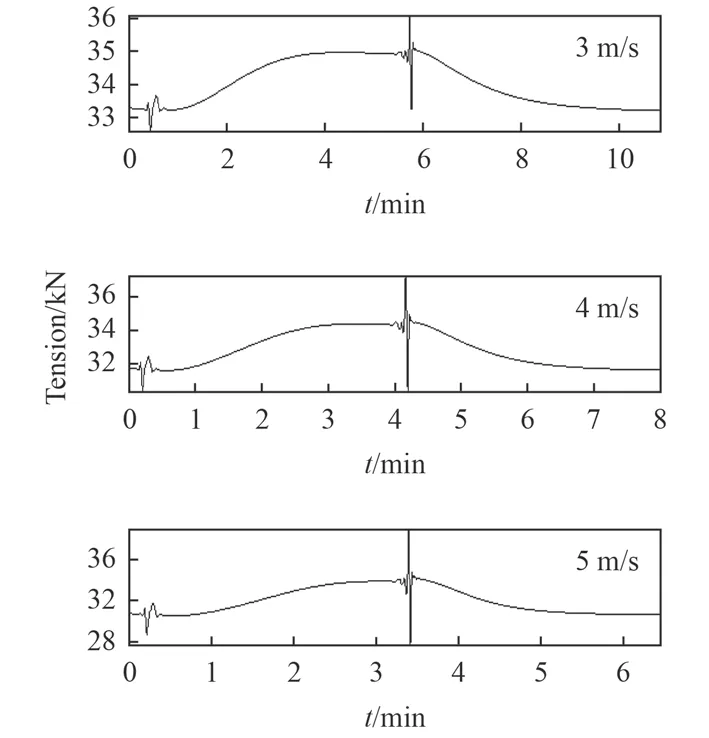
圖 5 不同拖曳速度對應的張力歷程Fig. 5 Cable surface end tension history in different towed velocity

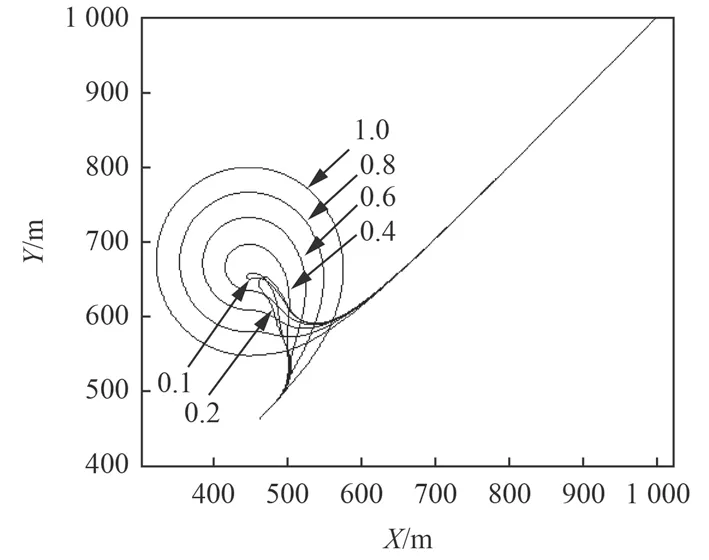
圖 6 不同回轉半徑下的拖曳體的水平面運動軌跡Fig. 6 Horizontal trajectory of towed body in differenttowed velocity

維持拖曳速度為2 m/s，改變回轉半徑，考察2 個階段的沖擊行為。當回轉半徑滿足R/L＜0.4 時，圖6 為拖曳體并未呈現出完整的回轉圈運動，圖7 為拖曳系統在小回轉圈運動時，拖曳體歷經了多次的升沉運動、這個升沉運動形成了多段沖擊效應，在這一階段拖曳系統受到的沖擊行為呈現出一定的非線性行為，由于纜在空間的一部分未參與到回轉圈運動，造成部分纜段的多次失速，形成了多次沖擊。如圖8 所示，當回轉半徑較小時，拖曳纜內的張力在回轉過程中歷經多次的振蕩，在完成整個小回轉圈的運動過程中幾乎不存在張力穩定的階段。

然而在R/L＞0.4 后逐漸呈現出了2 個階段的沖擊效應，拖曳體在回轉過程中不僅形成了完整的回轉圈，而且形成了穩定的沉降深度。

然而在R/L＞0.8 之后進入新的直航拖曳狀態時，拖曳體出現了一定的短時跌落和回升，這種跌論必然造成沖擊峰值。圖9 為拖曳系統在不同回轉半徑下沖擊峰值的分布規律，這種沖擊在R/L 接近1 時出現最大沖擊量。

3.3 拖曳系統其他結構參數對沖擊效應的影響

Wang[5]的研究顯示回轉圈半徑和纜長組合形成操縱參數，另一個操縱參數是拖曳體的水中重量和纜重量的比值，這反映了拖曳纜的質量分布情況。改變拖曳體的重量從而調整質量集中程度，可以改變拖曳系統的慣性效應。如圖10 所示，分別取不同的拖曳體水中重量，考查對2 個沖擊階段的影響規律，在較小的拖曳體重量的情況下第1 階段的沖擊效應幾乎觀察不到，第2 階段的沖擊效應也較為微弱，隨著拖曳體重量的增大，2 個階段的沖擊效應逐漸凸顯，可見拖曳系統的質量集中效應引起了較高水平的勢能向動能的轉化，從而造成了拖曳系統的沖擊效應越來越顯著。

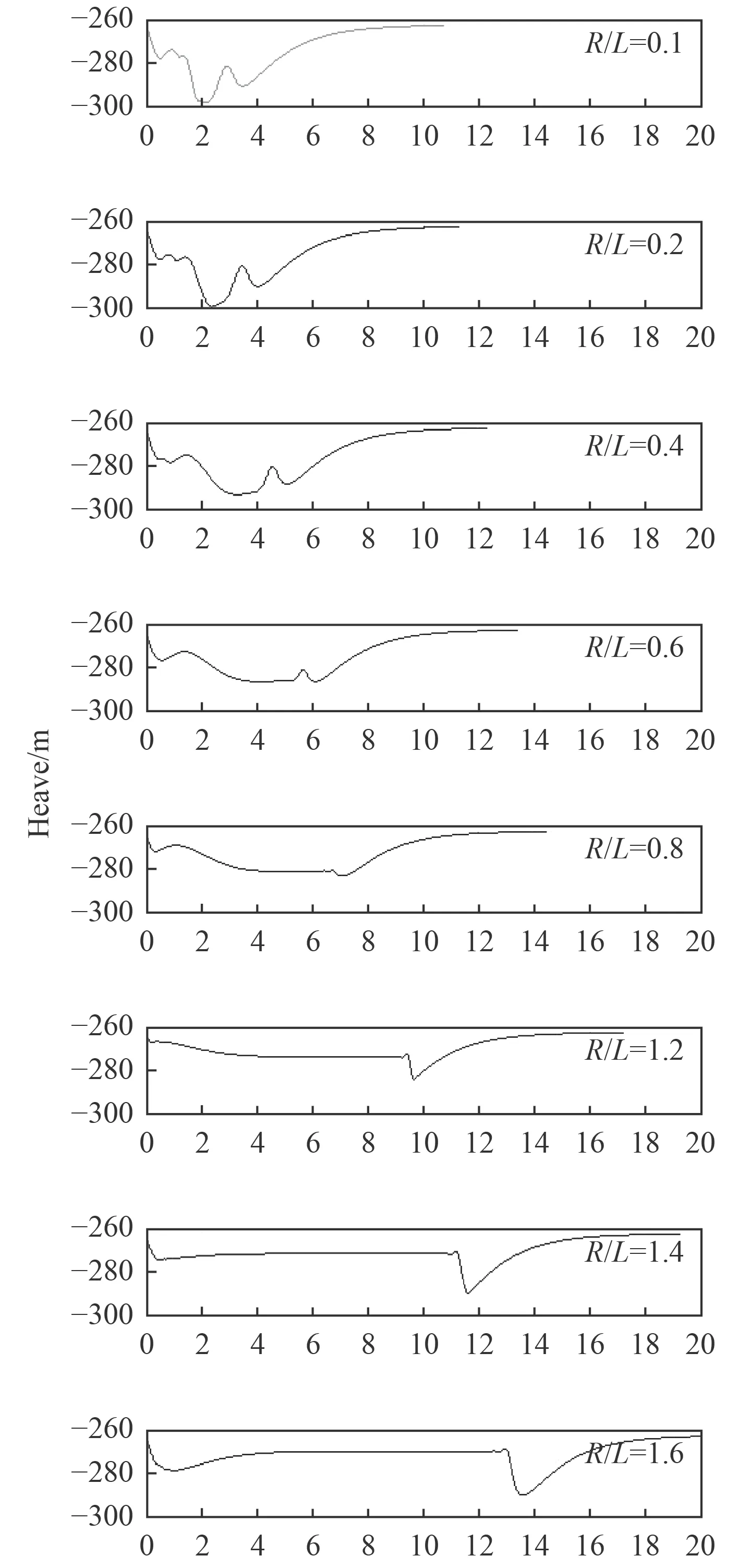
圖 7 不同回轉半徑對應的拖曳體升沉歷程Fig. 7 Heaving history of towed body in different turning radius

4 結 語

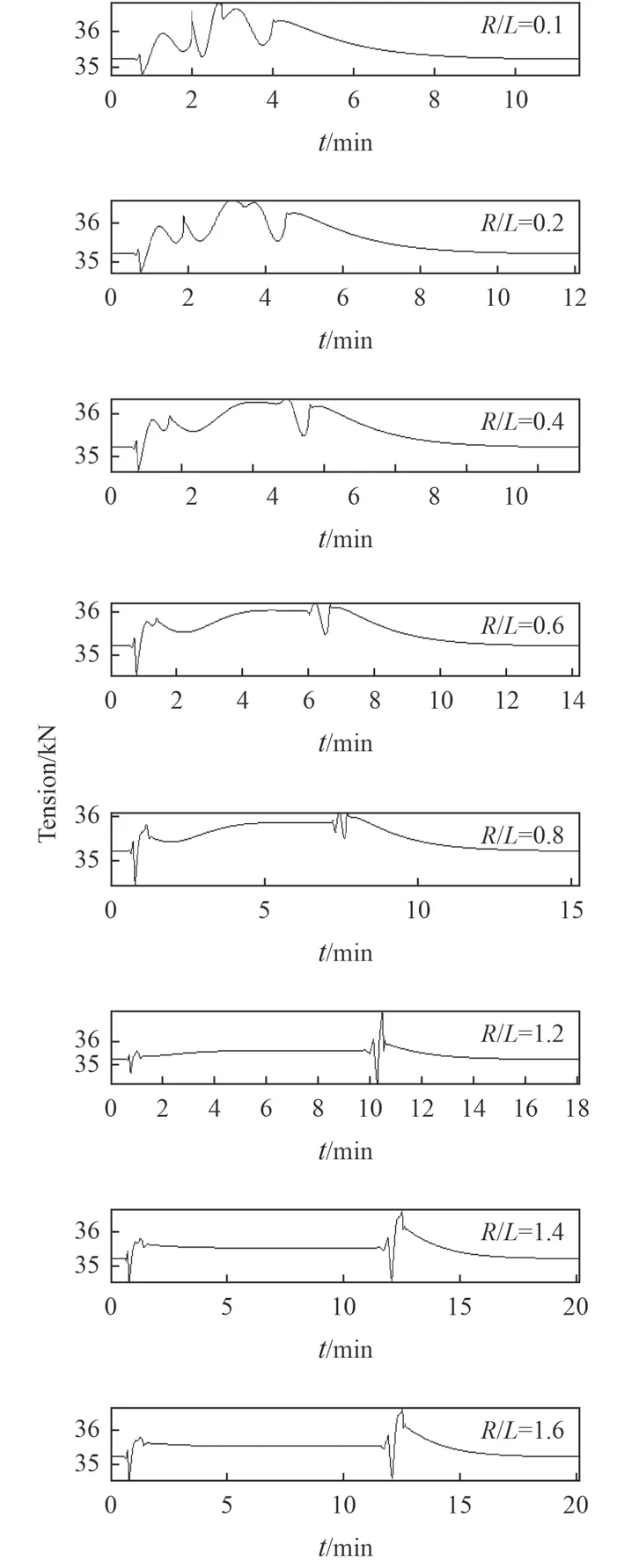
圖 8 不同的回轉半徑對應的沖擊張力的歷程Fig. 8 Cable surface end tension history in different turning radius

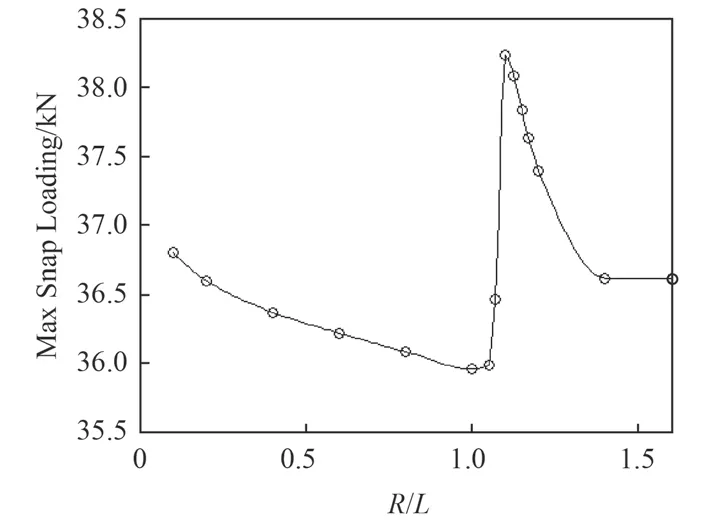
圖 9 最大沖擊張力隨著回轉圈運動的變化Fig. 9 The maximum snap loading in cable surface end vs. turning radius

本研究在建立相應數值方法的基礎上，改變拖曳系統的的結構參數和操縱參數。拖曳系統完成一次全回轉運動的過程中拖曳纜歷經多次沖擊作用，在較大回轉圈時對應了2 個沖擊階段，而在較小的回轉圈時，存在多次的沖擊效應體現了小回轉圈情況下的非線性行為。在進入較大的回轉圈運動時，拖曳系統歷經的沖擊效應尤其在R/L=1.0 附近出現了沖擊極值，這是由于進入直航拖曳過程中纜形的恢復延遲造成的。

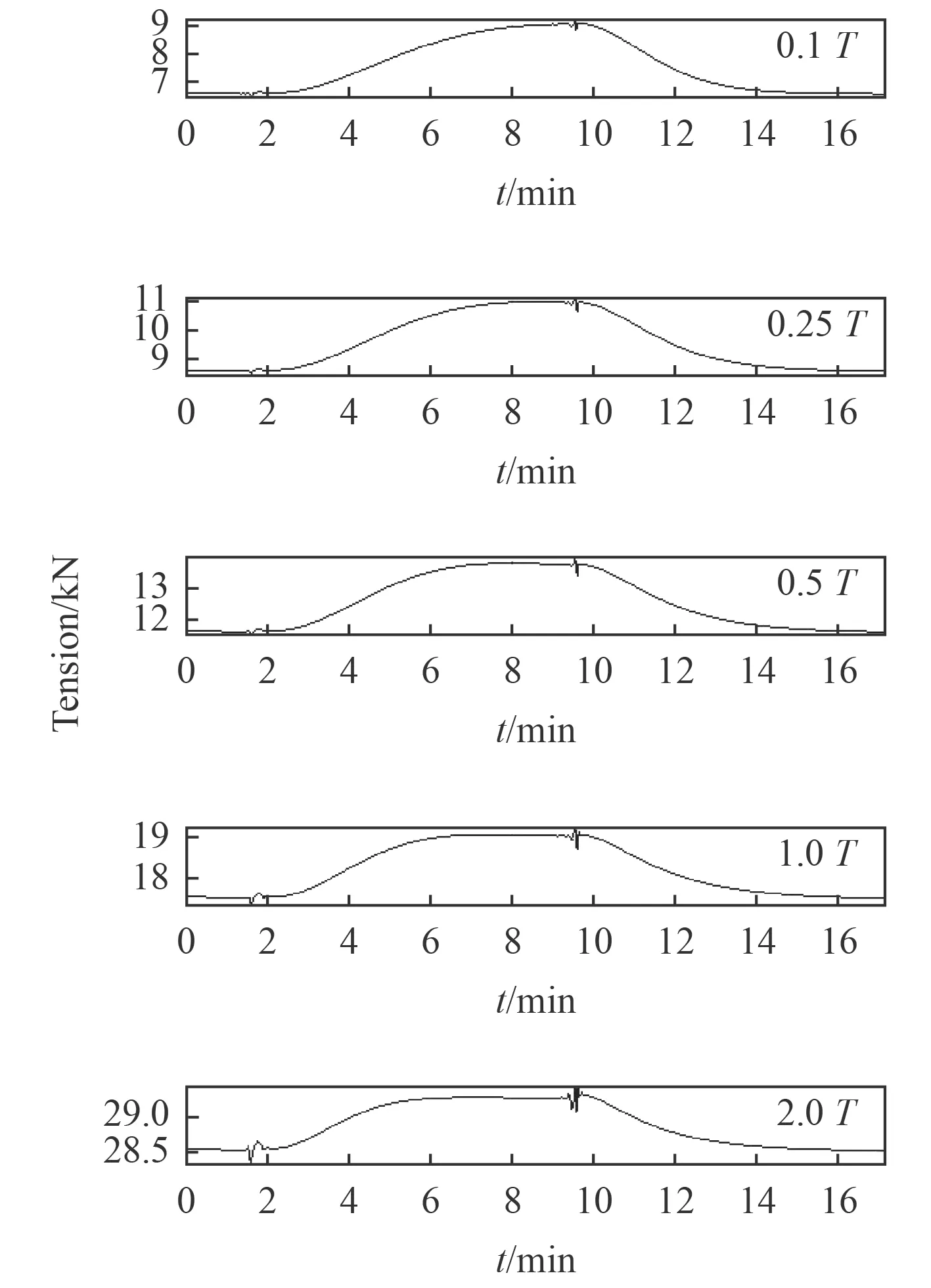
圖 10 不同的拖曳體重對應的沖擊張力歷程（R/L=1.0）Fig. 10 The snap loading in cable surface end ofdifferent towed body mass

拖曳系統的質量分布對沖擊效應的影響規律較為明顯，呈現低質量集中程度下的弱沖擊行為，高質量集中度的沖擊效應顯著。