基于ARMA模型下的我國消費價格指數預測

(四川大學 四川 成都 610065)

一、文獻綜述

楊堅(2014)認為CPI數據中存在季節性因素和周期性因素影響，并采用了ARIMA模型對12個月內的CPI數據進行了分析，實證表明了存在季節性與周期性因素影響。王維(2012)采用了混沌理論，針對CPI數據中存在的非線性特征進行了相空間重構，利用混沌網絡算法構建了短期內CPI的預測模型，并取得了較高的預測精度。范敬雅(2016)將CPI時間序列分解成細節序列與近似序列，針對近似序列采用SVM模型進行了擬合預測，有效提升了預測精度。孫冠華(2018)在BP網絡模型，RBF網絡以及和方法對傳統的通過ARMA模型分析預測居民消費價格指數進行了改進。

二、模型建立

(一)數據選取

本文從中國國家統計局網站選取了2014年1月至2019年5月的CPI的實際月度數據的同比增長指數數據。同比增長是指以上年同月為基期，展示出報告期與基期的水平之比，能夠很好的反映出指標的發展趨勢。

(二)數據的平穩性檢驗

圖一為2014年1月至2018年12月的我國居民消費價格指數數據，建立模型前，需要對該序列數據進行單位根檢驗，判斷該序列數據是否是平穩的。通過使用eviews7.0軟件計算其ADF結果如下圖，如圖二所示，ADF檢驗的t統計量小于1%顯著性水平下的臨界值，故該序列數據是平穩的，建立模型之前不需要進行差分

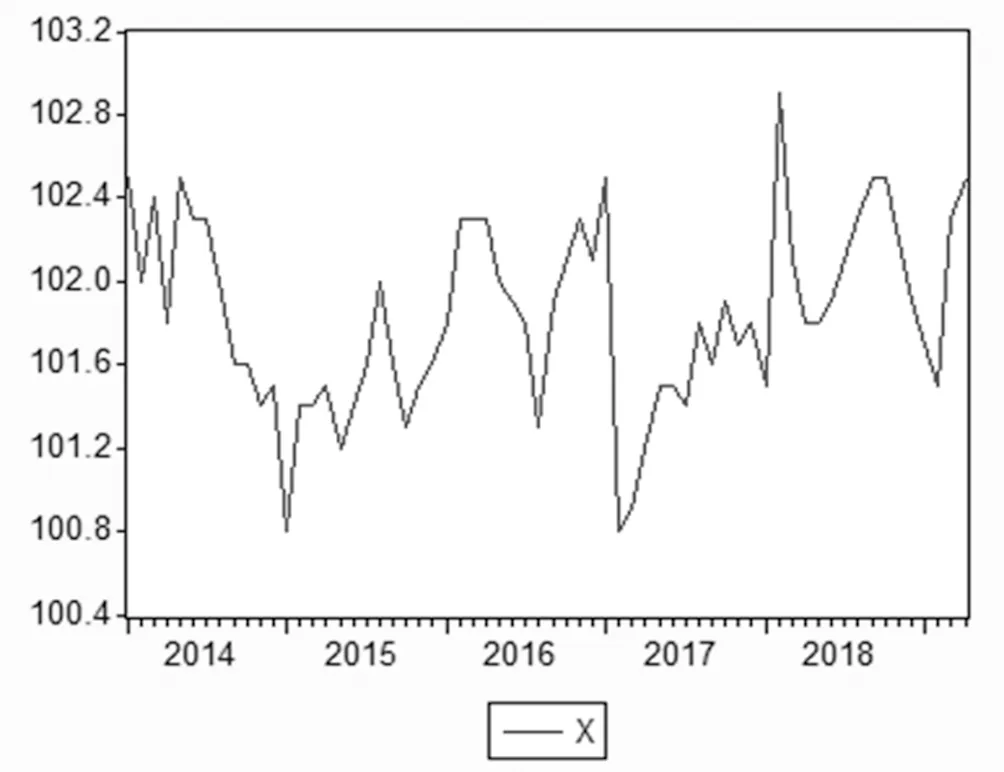
圖一

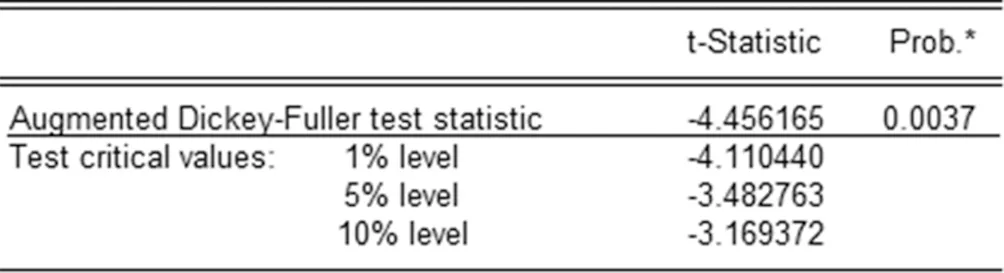
圖二

(三)模型建立

經過對該CPI序列的自相關和偏自相關圖的分析，初步建立模型ARMA(12，1)，ARMA(2,1)、AR(2)，運用最佳準則函數定價法進行反復篩選，綜合考察模型的整體擬合效果，確認模型如下

Xt=101.83+0.43Xt-2+εt+0.55εt-1

(四)模型平穩性檢驗

為了檢驗模型的平穩性，需要對模型特征根進行檢驗。若特征根的倒數都小于1，則表明本文建立的ARMA(2,1)模型是穩定的。經檢驗，特征根都落在單位園內，本文建立起來的模型是平穩的。

(四)殘差序列的獨立性檢驗

在模型參數估計后，模型殘差序列還需要進一步檢驗是否為純隨機序列。若殘差序列不隨機，則說明殘差序列中的存在有用信息可能被遺漏的情況，需要重新設定模型。通過對殘差序列的檢驗發現，Q統計量檢驗通過，殘差序列是純隨機的。即ARMA(2,1)從數據中充分提取信息是合理的。

(五)模型的預測

圖三是通過ARMA(2,1)模型得到的樣本預測值與實際值的擬合圖可以看出，模型的預測精度整體良好。

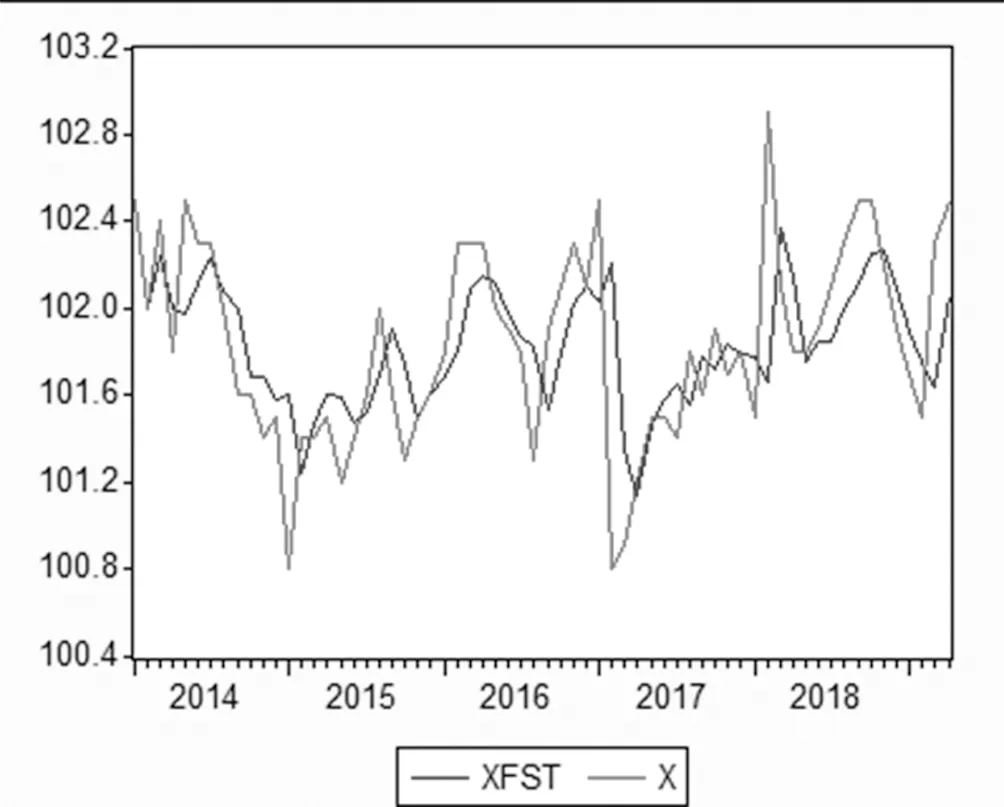
圖三

為了進一步分析研究全國居民消費價格指數的趨勢，我們利用所建立的ARMA(2,1)模型對2019年5月至12月的CPI指數做出了樣本外的動態預測。

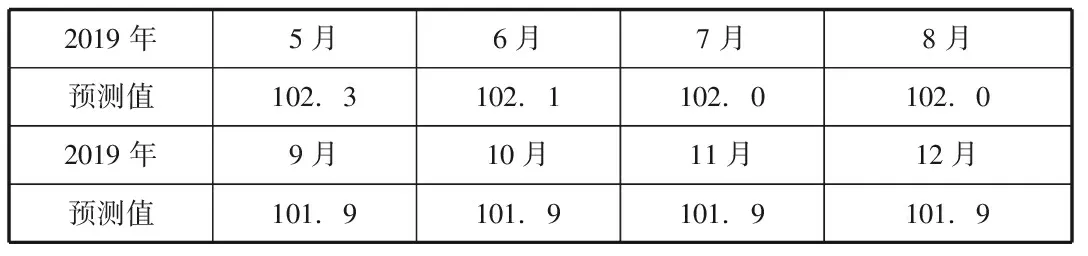
表一

三、結論

通過上述的分析和預測，可以發現2019年5月至2019年12月全國居民消費價格指數相對保持平穩，并成逐步下降的趨勢。