平面索牽引機(jī)構(gòu)工作空間解析求解與驗(yàn)證

何世凱，段清娟，李 浩，趙 萍

(西安電子科技大學(xué) 機(jī)電工程學(xué)院，陜西 西安 710071)

索驅(qū)動(dòng)機(jī)器人是一類使用索將所需的運(yùn)動(dòng)傳遞給末端執(zhí)行器的機(jī)器人，通過(guò)控制連接到末端執(zhí)行器的索長(zhǎng)度來(lái)移動(dòng)末端執(zhí)行器。其最令人矚目的成果是應(yīng)用于500m口徑球面射電望遠(yuǎn)鏡(Five-hundred-meter Aperture Spherical Telescope,FAST)的索牽引饋源系統(tǒng)[1]。

索驅(qū)動(dòng)機(jī)器人與傳統(tǒng)機(jī)器人相比，具有工作空間大、慣性小、制造成本低、易于組裝和重新配置等優(yōu)點(diǎn)，應(yīng)用廣泛，例如康復(fù)機(jī)器人系統(tǒng)[2]、運(yùn)動(dòng)攝像系統(tǒng)[3]以及航天虛擬作業(yè)訓(xùn)練系統(tǒng)[4]等。

在許多研究中，索驅(qū)動(dòng)機(jī)構(gòu)用于操作單個(gè)剛體，例如文獻(xiàn)[5]對(duì)索驅(qū)動(dòng)機(jī)械手的穩(wěn)定性進(jìn)行了研究，但是對(duì)于多體機(jī)構(gòu)的研究相對(duì)較少。索驅(qū)動(dòng)機(jī)構(gòu)要擴(kuò)展到多體機(jī)構(gòu)，需要解決的最基本的問(wèn)題是所需的索數(shù)量和多體機(jī)構(gòu)上的索分布[6]。文獻(xiàn)[6]提出一種分析索驅(qū)動(dòng)多體系統(tǒng)所需的索總數(shù)及其在各個(gè)剛體上的分布方法。

在索驅(qū)動(dòng)機(jī)構(gòu)中，存在的一個(gè)關(guān)鍵性問(wèn)題是索在工作時(shí)只受拉力。這一關(guān)鍵問(wèn)題與索驅(qū)動(dòng)機(jī)構(gòu)的工作空間密切相關(guān)[7]。文獻(xiàn)[7]對(duì)索驅(qū)動(dòng)機(jī)器人工作空間進(jìn)行了分類討論，當(dāng)索拉力t∈[0 ∞)時(shí)，末端執(zhí)行器能到達(dá)位置的集合，稱為力旋量封閉工作空間 (Wrench Closure Workspace, WCW)；當(dāng)索拉力t∈[tmin,tmax]，且tmin>0時(shí)，末端執(zhí)行器能到達(dá)位置的集合稱為力旋量可行工作空間 (Wrench Feasible Workspace, WFW)，且最為實(shí)用。文獻(xiàn)[8]提出了一種用于確定多體索驅(qū)動(dòng)機(jī)構(gòu)可控工作空間的方法。

上述文獻(xiàn)在求解工作空間時(shí)基于空間離散后逐點(diǎn)驗(yàn)證方法，并沒(méi)有給出解析的工作空間邊界，不能保證工作空間的連續(xù)性。筆者以平面兩桿三索機(jī)構(gòu)為例，找出其力旋量封閉工作空間邊界和力旋量可行工作空間，提出最大力旋量可行工作空間的優(yōu)化方法，并對(duì)前述理論進(jìn)行實(shí)驗(yàn)驗(yàn)證。

1 工作空間邊界

1.1 兩桿構(gòu)型及索拉力求解公式

為確保索牽引機(jī)構(gòu)中的所有索處于張緊狀態(tài)，至少需要n+1根索，其中n為系統(tǒng)的自由度數(shù)[6]。筆者基于此理論在最少索數(shù)量情況下進(jìn)行研究，分析有一端固定的兩桿索牽引機(jī)構(gòu)。

根據(jù)文獻(xiàn)[8]驅(qū)動(dòng)串聯(lián)兩桿機(jī)構(gòu)中共有兩種配置：[m1,m2]= [1,2]或者[0,3]，其中[1,2]表示第1根桿上牽引1根索，第2根桿上牽引2根索。同理，[0,3]表示第1根桿沒(méi)有牽引索，第2根桿上牽引3根索，分別對(duì)應(yīng)圖1(a)和圖1(b)。

圖1 兩桿三索的兩種配置

圖1中,O0X0Y0為基坐標(biāo)系，θi為桿中線相對(duì)于X0軸的夾角,qi為第i根桿中線相對(duì)于Y0軸的夾角，且順時(shí)針為負(fù)，逆時(shí)針為正，如圖1(b)q1為負(fù)；di為第i根索與連桿連接點(diǎn)到其轉(zhuǎn)動(dòng)副距離，Mi為第i個(gè)電機(jī)位置。

多體索牽引機(jī)構(gòu)中索力可以通過(guò)拉格朗日方程和虛功原理求解。根據(jù)文獻(xiàn)[9]可知

(1)

Q=JLT,

(2)

其中,L是拉格朗日函數(shù);Q為廣義力或廣義力矩;T為繩索拉力向量；φi為廣義坐標(biāo)，在文中的定義如圖1(a)所示;JL可表示為

其中，ti為第i根索單位向量，Ui為基坐標(biāo)系原點(diǎn)到索i在桿上牽引點(diǎn)的向量，m為牽引在機(jī)構(gòu)上的總索數(shù)。求解式(2)可得

T=JL+Q+ce，

(3)

其中,JL+是矩陣JL的偽逆，e是JL零空間中的任意單位向量，c是任意實(shí)數(shù)。

1.2 工作空間解析求解原理

1.2.1 工作空間邊界求解

從索力求解公式可看出，兩桿三索機(jī)構(gòu)中JL的零空間是一維的。可以通過(guò)分析其零空間找到此類機(jī)構(gòu)的力旋量可行工作空間的邊界。如果e的分量都是非零的，并且具有相同的符號(hào)，則可以取合適的c，使所有索的拉力都為正。

為了找到e，首先讓di是JL的第i列，它是與第i根索相關(guān)的列，由此可以得到

(4)

S是JL的前n列,可表示為

(5)

當(dāng)JL滿秩時(shí),可以假定S是滿秩的(可以通過(guò)改變JL中列的順序?qū)崿F(xiàn)),因此很容易得出JL的零空間向量nL,即

(6)

其中，S*是S的伴隨矩陣。當(dāng)S行列式為零時(shí)(即出現(xiàn)奇異JL不是滿秩)，上式中給出的nL的定義將有除零的情況。為了避免這一點(diǎn)，可以考慮nL的變形，命名為ε，可表示為

(7)

使用式(7)進(jìn)行計(jì)算,就可以避免奇異的情況。

由于ε的分量是廣義坐標(biāo)系下的連續(xù)函數(shù)，當(dāng)且僅當(dāng),其中的分量變?yōu)榱銜r(shí)將發(fā)生符號(hào)變化。因此，滿足零空間條件的區(qū)域的邊界是通過(guò)求解εi每個(gè)分量的根來(lái)確定的,即

(8)

其中,εi是ε的第i個(gè)分量。用等式(8)求解，可得到一組曲線，每條曲線將空間劃分為兩個(gè)區(qū)域，ε在兩個(gè)區(qū)域具有不同的符號(hào)。在每條曲線上，零空間向量的分量是零，也即為力旋量封閉工作空間的邊界。

1.2.2 兩種構(gòu)型求解

表1 [1,2]配置和[0，3]配置的參數(shù)

使用上述方法求解前述兩種構(gòu)型的力旋量封閉工作空間邊界，對(duì)圖1(a)，在[1,2]配置中，JL是2行3列的矩陣。JL的零空間可以使用關(guān)節(jié)變量θ1和θ2,即

(9)

所給出的方程是非線性的，因此有多個(gè)解。在本例中，式(9)的3個(gè)方程在θ1和θ2的平面中產(chǎn)生4條曲線，如圖2(a)所示,其坐標(biāo)軸范圍都取0到2π。其參數(shù)值如表1所示。

為了找出εi符號(hào)相同的區(qū)域，在θ1和θ2軸都以π/30為間隔進(jìn)行掃描，結(jié)果如圖2(a)所示。其中黑色區(qū)域是εi符號(hào)相同的區(qū)域，即為此系統(tǒng)力旋量封閉工作空間。由于角坐標(biāo)是周期性的，這些區(qū)域中的一些部分實(shí)際上是連接在一起的，最上面的部分和最下面的部分是可以拼接在一起的。接下來(lái)將第1根索牽到第2個(gè)桿上,從而形成第2種配置即[0,3],如圖1(b)所示。參數(shù)配置如表1所示。

圖2 兩種配置的求解結(jié)果

圖2(b)描繪了該機(jī)構(gòu)的[0,3]配置在給定構(gòu)型下的工作空間區(qū)域。根據(jù)圖2(b)可以看出,其力旋量封閉工作空間相對(duì)第1種配置明顯減小，這限制了規(guī)劃軌跡的范圍，有可能影響實(shí)際操作。筆者提出了一種優(yōu)化方法，優(yōu)化電機(jī)位置Mi和牽索點(diǎn)di，確保規(guī)劃的軌跡在力旋量可行工作空間內(nèi)的前提下，使得力旋量可行工作空間最大。這樣當(dāng)調(diào)整軌跡時(shí)，有較大的概率不用改變電機(jī)位置和牽索點(diǎn)，新的軌跡仍然在力旋量可行工作空間內(nèi)，從而節(jié)省了人工調(diào)整的時(shí)間，提高了工作效率。

圖3 優(yōu)化流程圖

2 最大力旋量可行工作空間優(yōu)化

2.1 優(yōu)化方法

以上討論的都是力旋量封閉工作空間，而在實(shí)際應(yīng)用中力旋量可行工作空間是更為實(shí)用的。而更大的力旋量可行工作空間意味著可以在更大的空間范圍內(nèi)進(jìn)行軌跡規(guī)劃，從而使機(jī)構(gòu)完成預(yù)想的實(shí)驗(yàn)或工作。在此使用蒙特卡羅方法對(duì)電機(jī)位置Mi和牽索點(diǎn)di進(jìn)行優(yōu)化，在保證規(guī)劃的軌跡在力旋量可行工作空間內(nèi)的前提下，找出力旋量可行工作空間最大的配置。優(yōu)化流程圖如圖3所示。

2.2 優(yōu)化實(shí)例

以兩桿[1,2]配置為例，為了讓兩桿機(jī)構(gòu)在運(yùn)動(dòng)過(guò)程中能平穩(wěn)加速、準(zhǔn)確停止，一般采用梯形速度曲線控制運(yùn)動(dòng)過(guò)程。筆者設(shè)計(jì)的兩桿運(yùn)動(dòng)如圖4所示，q1在10 s內(nèi)先加速再勻速再減速達(dá)到15°，然后再以此趨勢(shì)先加速再勻速再減速在30 s時(shí)達(dá)到-15°，最后再經(jīng)過(guò)一次加速勻速減速的過(guò)程達(dá)到起始位置。q2的變化趨勢(shì)與q1相同，不過(guò)其角度變化為30°。ω1和ω2分別代表筆者設(shè)計(jì)的兩桿運(yùn)動(dòng)的兩桿角速度。

圖4 軌跡規(guī)劃

根據(jù)實(shí)際電機(jī)扭矩情況限制索拉力范圍為[5 N,200 N]，即索拉力在此范圍內(nèi)機(jī)構(gòu)所能達(dá)到的位置的集合為力旋量可行工作空間。以拉力的二范數(shù)最小為目標(biāo)求解拉力,即

(10)

優(yōu)化結(jié)果即為圖5(a)所示，圖5(a)對(duì)應(yīng)的參數(shù)見(jiàn)表1。為了對(duì)比優(yōu)化結(jié)果，隨機(jī)選取了一組未優(yōu)化的參數(shù)配置結(jié)果,如圖5(b)所示，具體參數(shù)值不再贅述。

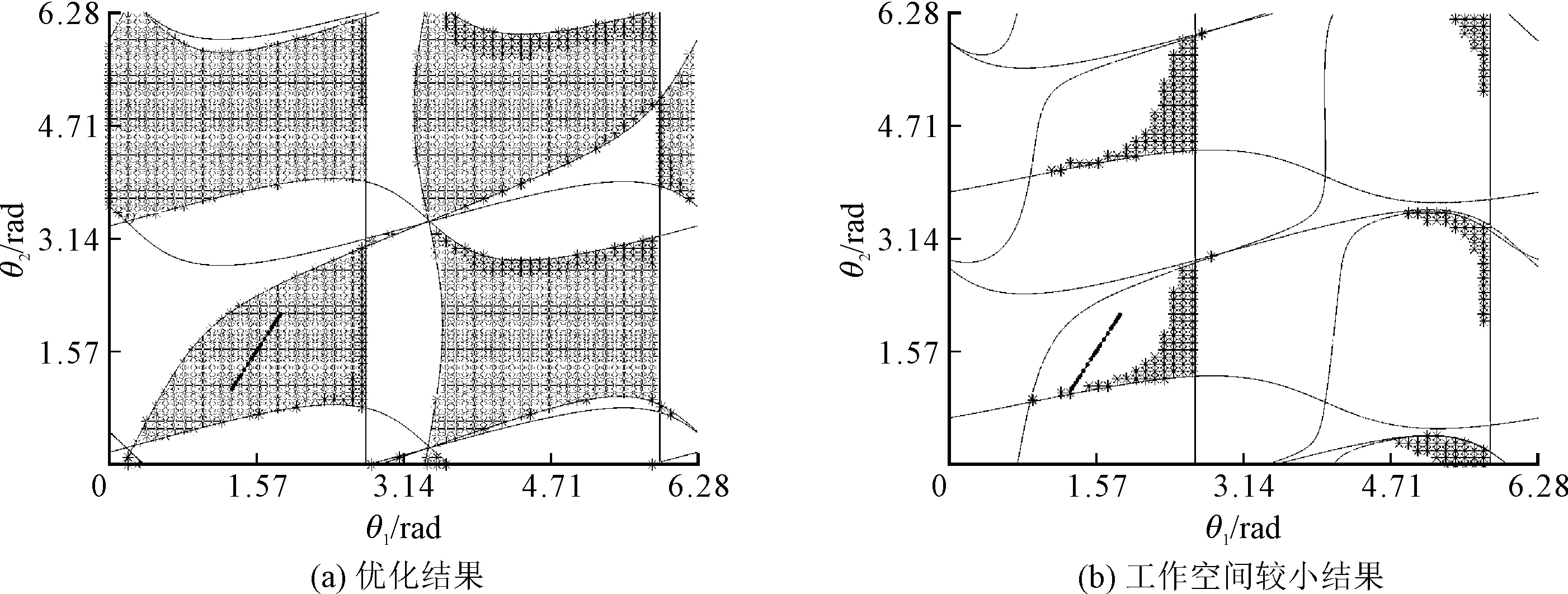
圖5 優(yōu)化結(jié)果與對(duì)比結(jié)果

圖5中黑色區(qū)域和淺色區(qū)域共同組成力旋量封閉工作空間，淺色區(qū)域?yàn)榱π靠尚泄ぷ骺臻g，黑色線段為圖4中規(guī)劃的q1和q2轉(zhuǎn)換為θ1和θ2即機(jī)構(gòu)的軌跡圖。兩圖中力旋量可行工作空間大小區(qū)別明顯，圖5(b)力旋量可行工作空間的點(diǎn)數(shù)為1 164，圖5(a)為1 912，圖5(b)僅為圖5(a)的60%。

3 實(shí)驗(yàn)驗(yàn)證

3.1 實(shí)驗(yàn)平臺(tái)

由第2節(jié)優(yōu)化結(jié)果可知,表1中的配置工作空間較大，所以依表1中的數(shù)據(jù)進(jìn)行實(shí)驗(yàn)驗(yàn)證。

實(shí)驗(yàn)平臺(tái)如圖6所示,平臺(tái)框架的長(zhǎng)寬高分別為2 000 mm、2 000 mm、2 000 mm。電機(jī)和驅(qū)動(dòng)器固定在鋁框上，索通過(guò)兩個(gè)滑輪繞在電機(jī)上。通過(guò)電機(jī)的正反轉(zhuǎn)控制索的收放，從而帶動(dòng)桿件的運(yùn)動(dòng)。通過(guò)連接在鋁框內(nèi)滑輪2的拉力傳感器，采集索拉力的大小；通過(guò)目標(biāo)運(yùn)動(dòng)跟蹤裝置MARS2H采集桿件上關(guān)鍵點(diǎn)位置數(shù)據(jù)，計(jì)算出實(shí)際q1和q2，并與理論值進(jìn)行對(duì)比。

圖6 實(shí)驗(yàn)平臺(tái)

3.2 實(shí)驗(yàn)結(jié)果

實(shí)驗(yàn)結(jié)果如圖7和圖8所示。

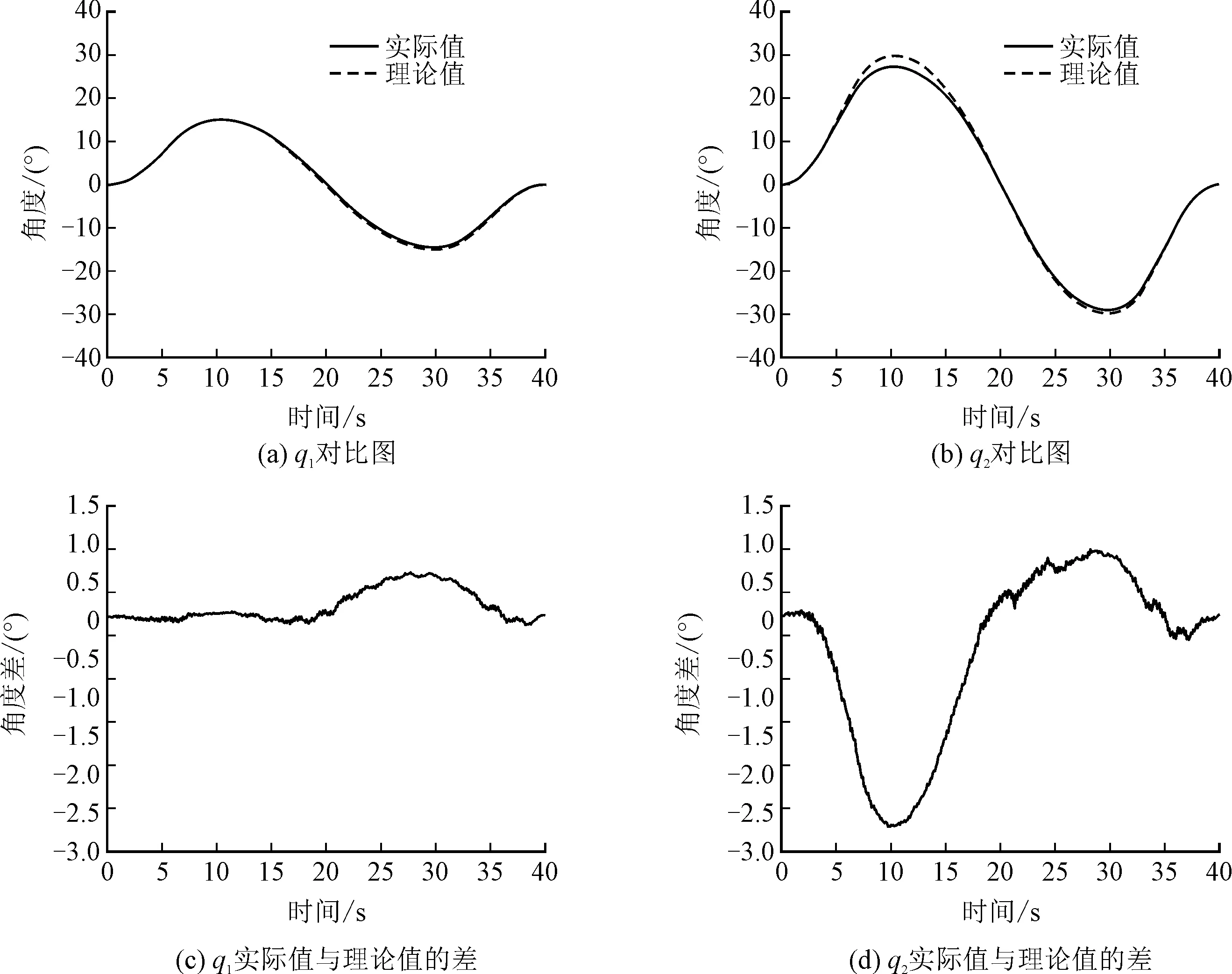
圖7 理論軌跡與實(shí)際軌跡對(duì)比

圖8 三索拉力理論值與實(shí)際值

從圖7可以看出，在大部分時(shí)間，實(shí)際角度值與理論角度值基本吻合，出現(xiàn)誤差的時(shí)間較短,且誤差大的時(shí)刻都是在桿的轉(zhuǎn)動(dòng)方向發(fā)生改變的時(shí)刻。

在10 s處q2的誤差最大,且實(shí)際角度未達(dá)到理論的角度,這就導(dǎo)致索的張緊索力增大，從實(shí)際索力圖可以看出,索2拉力和索3拉力與理論值相比有較大的誤差,且比理論值大。根據(jù)力矩平衡原理，索2和索3拉力的增大,導(dǎo)致索1的拉力隨之增大。接著從角度對(duì)比圖可以看出,q1和q2在20～30 s區(qū)間內(nèi)誤差逐漸增大，實(shí)際角度逐漸落后于理論角度,且在30 s時(shí)這個(gè)誤差達(dá)到此區(qū)間最大。同理，這將導(dǎo)致實(shí)際情況中3根索力都增大,且在30 s左右實(shí)際值與理論值的偏差達(dá)到最大。30 s之后角度誤差減小，實(shí)際拉力也逐漸接近于拉力的理論值。

由圖8可以看出,實(shí)際拉力基本保持在5 N～200 N之間，這也進(jìn)一步說(shuō)明了優(yōu)化出的構(gòu)型可以保證軌跡在力旋量可行的工作空間內(nèi)。

4 結(jié)束語(yǔ)

文中針對(duì)平面多體索牽引機(jī)構(gòu)提出了零空間的方法求解力旋量封閉工作空間邊界的解析方程，此方法適用于單冗余的平面索牽引多體機(jī)構(gòu)。并在此基礎(chǔ)上掃描出力旋量可行工作空間。使用蒙特卡羅方法優(yōu)化配置使得力旋量可行工作空間最大。根據(jù)優(yōu)化出的結(jié)果進(jìn)行實(shí)驗(yàn)，驗(yàn)證了此配置的正確性即機(jī)構(gòu)運(yùn)行過(guò)程中拉力始終保持在規(guī)定范圍內(nèi)。

蒙特卡羅優(yōu)化方法只是大規(guī)模抽樣，并不能找出所有的配置進(jìn)行分析從而找到最優(yōu)的配置，而分析所有配置又會(huì)導(dǎo)致效率低下。后續(xù)會(huì)對(duì)此問(wèn)題進(jìn)一步研究,找出更好的優(yōu)化方案。