基于遺傳算法的變速風電機組傳動鏈加阻器自整定

文 | 萬宇賓，劉紅文，蔣韜，胡嬋娟

對于采用“增速齒輪箱+高速發電機（雙饋或高速永磁）”傳動鏈形式的風電機組，其傳動鏈一階扭轉振動模態的固有阻尼通常較低，在機組發電運行過程中（特別是在恒轉速運行區段），當風速變化較快或穿越電網故障時，傳動鏈模態可能受到較強的激發。在發電機轉矩指令中疊加一個變化的分量可使傳動鏈模態的等效阻尼得以提升，從而有效抑制扭振、降低疲勞載荷，此項技術被稱為傳動鏈加阻，目前已廣泛應用于兆瓦級風電機組。

經典的加阻器結構較簡單（通常為一個含超前補償的帶通濾波器），參數整定難度不大。但近年來，隨著風輪直徑和塔架高度的不斷增加，與傳動鏈模態耦合的風輪面內模態和塔架側向模態變得更易于激發，需要重點關注。此外，為降低度電成本，面向特定場址的精細化、定制化設計逐漸成為常態，這使得風電機組對于工程不確定性的容納能力在客觀上呈下降趨勢。上述背景下，設計者須對加阻器作更為精細的設計和調節，以充分抑制傳動鏈及其耦合模態的激發，經典的加阻器結構往往難以提供最優的加阻性能，采用相對復雜的加阻器結構可更好地逼近最優，但其參數數量及整定難度也相應增加，采用手動整定時，對工程師的經驗和設計水平有更高的要求，設計質量相對難以保證。

針對上述情況，本文提出一種基于自適應遺傳算法的傳動鏈加阻器自整定框架，該框架考慮了幾種典型的加阻濾波器結構，允許利用先驗信息和參數物理意義施加約束，并根據期望的時、頻域指標定義了適應度函數，利用遺傳算法的尋優能力實現加阻器參數自整定。

傳動鏈加阻器自整定框架

一、傳動鏈加阻基本原理

傳動鏈加阻技術的基本原理可表述為：通過設計適當的加阻器（DTD），從發電機轉速測量值中提取扭振速度分量，并據此構造一個與扭振速度相位相近、幅值成正比的傳動鏈加阻轉矩分量，疊加到轉矩指令中，使得閉環系統中傳動鏈模態的等效阻尼得以提升。控制結構如圖1所示，其中，、ωgen為發電機轉速指令和反饋，、為發電機轉矩指令的PI分量和加阻分量，Ta為氣動轉矩。

傳動鏈加阻器的手動整定多采用極點配置，一般應符合以下原則：

（1）在待加阻頻率附近具有較高的增益，以實現足夠的加阻；

（2） 在低、高頻段具有相對較低的增益，避免引入不期望的功率波動或噪聲；

（3）在待加阻頻率附近具有接近0度的相移。

二、典型加阻濾波器結構

工程上常用的加阻濾波器包括但不限于以下形式：

1.單一帶通濾波器（BPF）

二階帶通濾波器傳遞函數如下：

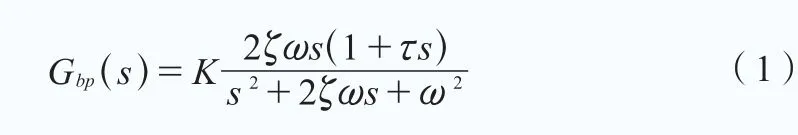
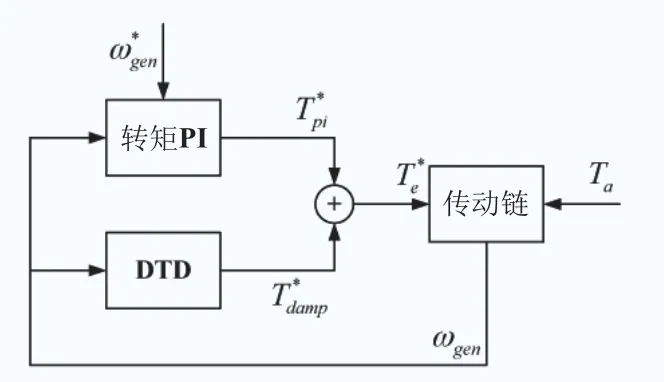
圖1 傳動鏈加阻控制結構

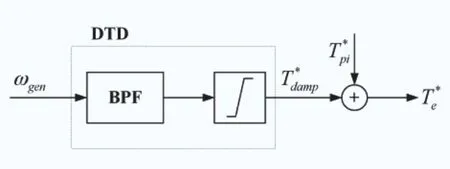
圖2 基于單一帶通濾波器的傳動鏈加阻器

式中，K為加阻增益，ζ為阻尼，ω的取值應接近未加阻時的自然振蕩頻率，τ用于調整相移、補償時延和改變濾波器特性。

2.多個帶通濾波器并聯

這種結構適用于需對多個相隔較遠的模態同時進行加阻的情況，每個帶通濾波器的頻率取值應分別接近這些模態。

3. 帶通濾波器與帶阻濾波器（Notch）串聯

相對于前面兩種，這種結構的特點在于其具有更高的設計自由度和更豐富的幅頻特征表達能力，理論上可實現更優的加阻性能，但由于其參數數量較多，且取值與模態頻率無明確的對應關系，參數整定相對較困難。二階帶阻濾波器傳遞函數如下：

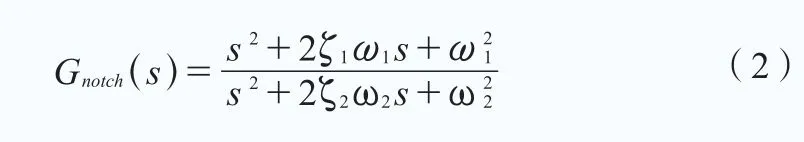
三、自適應遺傳算法

1. 自適應遺傳算法簡介

遺傳算法（GAs）是一類模擬生物進化過程的全局優化算法。在其優化過程中無需對目標函數進行反演，也不要求目標函數可導，對各類優化問題具有廣泛的適應性。作為遺傳算法的主要操作算子，交叉和變異在很大程度上決定了GAs的搜索特性。在簡單遺傳算法（SGA）中，交叉概率和變異概率取常數，難以在搜索效率和避免局部最優間取得平衡。針對SGA的不足，Srinivas等人提出自適應遺傳算法（AGA），AGA在SGA基礎上加入了交叉、變異概率的自適應律，既保持了啟發式搜索的效率優勢，也使種群得以維持一定的多樣性。

對于上文介紹的幾種加阻器結構，除單個帶通濾波器較簡單外，其余類型均需整定較多參數，搜索空間維度較高，同時期望算法盡可能避免陷于局部最優，故選擇AGA作為自整定框架的優化算法。

2. 約束設計

合理利用先驗信息和參數物理含義施加約束可顯著縮減搜索空間。具體而言，結合兆瓦級風電機組的典型模態頻率，濾波器頻率參數ω的搜索范圍可限定于5～25 rad/s，當ω與模態頻率存在明確對應關系時（例如：并聯的多個帶通濾波器），可直接指定ω數值從而降低搜索維度，也可將ω的范圍限制在模態頻率附近；根據物理含義，所有濾波器阻尼參數ζ限定于0.05～0.95；考慮典型轉矩指令、速度反饋傳輸時延，所有時間常數τ限定于0.01～0.07 s；根據一般經驗，增益參數搜索范圍可限定于10～1000。以上約束設計適用于本文選取的設計對象，對于其他機型可作適當調整。此外，施加更精準的約束有利于進一步縮短參數自整定過程，但可能并非必要。

3. 適應度函數設計

遺傳算法中，適應度函數用于個體的性能評價，并直接決定了優化的傾向。針對加阻器參數整定及優化設計目標，選取低速軸轉矩對發電機轉矩指令的階躍響應為主要考察對象，提出以下2種適應度函數：

（1）低速軸轉矩變化率絕對值積分，其離散形式可寫為：

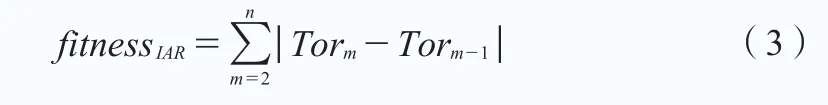
（2）時間加權低速軸轉矩變化率絕對值積分，其離散形式可寫為：

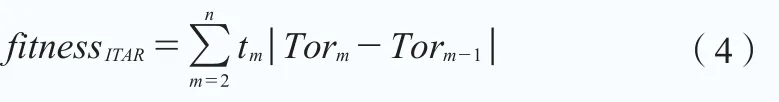
以上兩式中，n為階躍響應的采樣點數，Tor為低速軸轉矩采樣值，t為時間采樣值。

在適應度函數中需要體現的其他限定條件以懲罰形式實現。當加阻器開環幅頻特性高、低頻段增益高于預設值，以及加入加阻器后系統增益裕度、相角裕度低于預設值時施以懲罰，即：

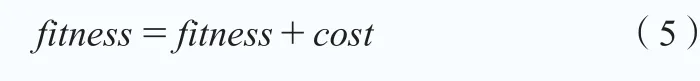
式中，cost為預設的懲罰值。

參數整定測試及評估

以某型2MW雙饋機組為原型進行加阻器自整定及對比評估，機組在16m/s風速下的傳動鏈及耦合模態信息如下：

考慮2種適應度函數、3種加阻器結構，在Matlab環境下進行加阻器自整定測試，將整定結果用于傳動鏈模型，結合加阻器開環特性、加阻前后傳動鏈系統開環特性、加阻前后低速軸轉矩對發電機轉矩指令階躍響應對加阻器性能進行評估，遺傳算法種群個數取100，精英個數取2。

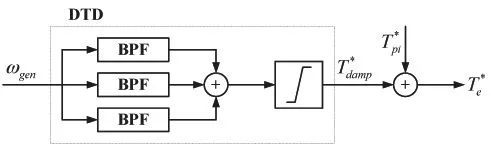
圖3 基于多個帶通濾波器并聯的傳動鏈加阻器

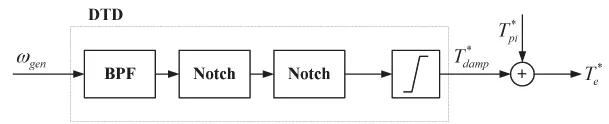
圖4 基于帶通濾波器與帶阻濾波器串聯的傳動鏈加阻器

一、情況1：單一帶通濾波器，IAR，待整定參數4個

最優個體適應度為711.8255，對應參數：

K=591.5795；ω =7.9809；ζ=0.3721；τ=0.0501

具體結果如圖5所示。

二、情況2：多個帶通濾波器并聯，IAR，待整定參數12個

最優個體適應度為529.6658，對應參數：

K1=613.3398；ω1=7.2499；ζ1=0.2777；τ1=0.0169

K2=281.5164；ω2=16.4169；ζ2=0.7114；τ2=0.0102

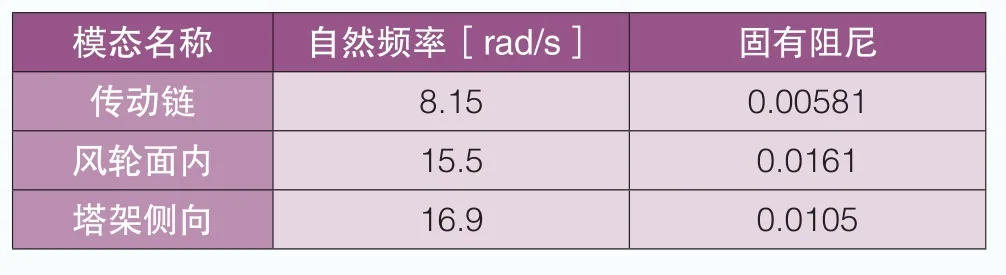
表1 原型機模態信息

圖5 情況1整定結果（左上、右上、左下、右下依次為：遺傳算法進化曲線、加阻器開環特性、加阻前后傳動鏈系統開環特性、加阻前后低速軸轉矩對發電機轉矩指令階躍響應，圖6-圖7類同）

K3=766.3081；ω3=17.8995；ζ3=0.1327；τ3=0.0132

具體結果如圖6所示。

三、情況3：帶通濾波器與帶阻濾波器串聯，IAR，待整定參數12個

最優個體適應度為481.9224，對應參數：

K= 937.4840；ω =9.5624；ζ=0.8524；τ=0.0116

ω1A=11.5252；ζ1A=0.6784；ω2A=24.3169；ζ2A=0.2117

ω1B=119.9109；ζ1B=0.7387；ω2B=8.7462； ζ2B=0.7934

具體結果如圖7所示。

四、情況4：單一帶通濾波器，ITAR，待整定參數4個

最優個體適應度為2247.2103，對應參數：

K= 443.6622；ω =12.9089；ζ=0.9145；τ=0.01579

圖示從略。

五、情況5：多個帶通濾波器并聯，ITAR，待整定參數12個

圖6 情況2整定結果

最優個體適應度為1008.3327，對應參數：

K1=488.4967；ω1=8.2298；ζ1=0.3255；τ1=0.0150

K2=184.9247；ω2=16.3280；ζ2=0.5651；τ2=0.0102

K3=692.6088；ω3=17.1328；ζ3=0.0577；τ3=0.0692

圖示從略。

六、情況6：帶通濾波器與帶阻濾波器串聯，ITAR，待整定參數12個

最優個體適應度為999.2987，對應參數：

K= 964.8767；ω =11.0582；ζ=0.4080；τ=0.0201

ω1A=19.1263；ζ1A=0.9062；ω2A=12.3245；ζ2A=0.7058

ω1B=11.9740；ζ1B=0.0657；ω2B=18.1132；ζ2B=0.2277

圖示從略。

七、對比分析

表2對各種情況下的傳動鏈系統開環幅頻特性進行了匯總，可見：

（1）6種情況下的整定結果均可實現對傳動鏈模態的有效加阻，傳動鏈模態由加阻前的78.6dB降至50dB左右，滿足基本設計要求；

（2）關于適應度函數：對于傳動鏈模態，IAR指標（情況1—3）下的抑制效果略優于ITAR指標（情況4—6）；對于風輪面內和塔架側向模態，則恰恰相反，ITAR指標較優。對上述結果的合理解釋是：IAR不考慮時間加權，因此該指標更傾向于抑制波動量值上占主導影響的傳動鏈模態，對于風輪面內、塔架側向模態的抑制則有所忽略甚至犧牲；ITAR指標引入了時間加權，對階躍響應的后期給予了較高的權重，因此更有利于實現對各模態的均衡抑制；

（3）關于加阻器結構：可以看出，在IAR、ITAR兩種指標下，單一帶通濾波器（情況1、4）均難以實現對風輪、塔架模態的有效抑制；帶通濾波器并聯結構（情況2、5）與帶通帶阻串聯結構（情況3、6）的表現基本相當，且均優于單一帶通濾波器，能較好地兼顧傳動鏈、風輪、塔架模態的抑制。

圖7 情況3整定結果

結論

傳動鏈加阻器參數自整定框架將繁瑣的人工調節工作轉化為對性能指標及約束條件的規劃設計，具有較好的應用價值。基于本文參數整定測試及評估結果，可得出以下結論：

（1）對于相同的適應度指標，一般而言，結構較復雜的加阻器可實現更優的加阻性能，這在很大程度上得益于其更強的頻率特性表達能力；

（2）對于相同的加阻器結構，適應度函數的構造對于優化結果有較大影響，IAR指標偏重于階躍響應的前期快速收斂，但對于耦合模態的加阻性能相對較差；ITAR指標可較好地兼顧各個模態的加阻，對加阻器設計的適應性更好；

表2 傳動鏈系統開環幅頻特性對比

（3）本文研究工作局限于模型精確已知條件下的離線參數自整定，如何將該框架在線地應用于存在參數不確定性的實物機組，仍是值得進一步研究的課題。