高中數學函數零點解決方法探究

劉小龍

（巴中市第三中學，四川 巴中 636600）

一、根據函數圖像解決函數零點問題

已知函數f(x)=logax+x-b（a＞0,且a≠1）,當2＜a＜3＜b＜4時，函數f(x)的零點x0∈（n,n+1）,n∈N*,則n=（）

[常規解法]：設f(x0)=0，因為f(x)=logax+x-b，又2＜a＜3＜b＜4，所以f(1)=loga1+1-b=1-b＜0

因為2＜a＜3＜b＜4，

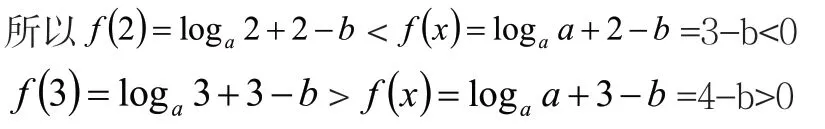
綜上，x0∈（n,n+1），因此n=2

[圖像解法]：在直角坐標系下分別作出y=log2x，y=log3x及y=3-x,y=4-x的圖像，所有可能的交點構成了圖中的陰影區域（不含邊界），其中各點的橫坐標都坐落在（2,3）以內，又因為x0∈（n,n+1），n∈N*，所以n=2。

要進一步強化學生針對零點問題的求法，掌握函數和方程之間的轉化技巧，另外還要引導學生學會利用數形結合的方法來判斷零點的個數，零點所在區間。在高考問題中，考查函數性質和方程根與系數關系的綜合運用題一般難度較大，因此要在日常的學習中有所準備，加強訓練。

二、利用零點性質求參數的取值范圍

1.f(x)=x3-6x2+9x+a在x∈R上有三個零點，求a的取值范圍。

解：由f'(x)=3x2-12x+9=3(x2-4x+3)=3(x-3)(x-1)得

令f'(x)＞0,得x＞3或x＜1,f'(x)＜0,

得1＜x＜3

所以f(x)在（-∞，1），（3，+∞）上單調遞增，在（1,3）上單調遞減。

所以f(x)極大值=f(1)=4+a＜0，a＞-4

f(x)極小值=f(3)=a＜0

所以-4＜a＜0.

2.方程x3-ax2+9x+a=0在[2,4]上有實數解，求a的取值范圍。

解：由方程x3-ax2+9x+a=0在[2,4]上有實數解

即x3-ax2+9x=-a，

由f(x)=x3-ax2+9x的圖像可得

0≤a≤4

3.x3-ax2+9x=0在[2,4]上有實數解，求a的取值范圍。

在解決函數零點存在的區間或者方程根的個數問題時，主要采用的方法有函數零點定理和利用函數圖象來進行判斷。根據函數零點的性質，求參數的取值范圍主要采用數形結合、等價轉換以及分類討論等方法。學生在解題過程中要注重利用導數求出函數的單調區間、畫出函數的圖象等方法，能夠有效解決和零點相關的問題。