基于改進的蟻群算法的測試數據自動生成方法

文/苗曉旭 胡玉露 徐豪 曾佩杰

1 引言

隨著軟件規模的逐漸增大和軟件復雜度的不斷提升，傳統手工編寫測試數據的方法已不再適用。高效可行的測試數據自動生成方法不僅能保證測試覆蓋率，還可以較大程度降低測試成本，對自動化的軟件測試來說意義重大。

目前，測試數據自動生成方法主要有動態、靜態和智能優化三類方法。動態法有迭代松弛法、試探法、程序插樁法等；靜態法有符號執行法、隨機法；智能優化算法有禁忌搜索算法、蟻群算法、遺傳算法等。

蟻群算法的搜索過程采用分布式計算方式，相較其它智能算法具有較高的計算能力和運行效率，但算法的搜索精度仍有待完善。因此本文提出改進的蟻群算法，在傳統蟻群算法的基礎上引入相似度影響因子，能夠增加算法的全局搜索能力。并將改進的蟻群算法應用到測試數據自動生成問題中。

2 測試數據自動生成模型

設待測路徑為P，采用改進的蟻群算法自動生成的輸入參數變量為X={x1，x2，…，xn}，輸入參數變量X的實際執行路徑為P’，當P’=P時，所取的X則為最優測試數據。

測試數據自動生成模型主要包括以下三個基本模塊：

（1）程序分析模塊：靜態分析被測程序的語義、語法和詞法，生成測試路徑總集。從總集中任選一條邏輯路徑并以此為基礎插樁生成插樁程序。最后分析并確認輸入變量集合。

（2）算法解算模塊：根據輸入變量集合，對變量編碼組合生成初始蟻群；根據被測插樁程序的運行結果反復進行編碼的迭代更新，直到找到最優解或達到最大迭代次數。

（3）驅動程序模塊：獲取輸入的測試數據變量，調用并運行樁程序，對每個測試數據完成評價后反饋給算法解算模塊。如圖1所示。

3 改進的蟻群算法設計

3.1 蟻群算法

蟻群算法是一種仿生優化算法，模擬了螞蟻在運輸食物過程中搜索選擇食物源到蟻穴的最短運輸路線的過程。通過追尋具有大濃度信息素的路線舍棄具有低濃度信息素的路線，同時在運輸過程中受到自身信息素釋放及信息素揮發的影響，蟻群不斷修正運輸路線，最終找到一條信息素濃度最大也是距離最短的運輸路線。從仿生模擬過程可以看出來，蟻群算法是具備進化能力的隨機搜索算法，通過對備選解集合的不斷迭代優選來尋求最優解。迭代優選過程主要包括兩個階段：適應階段和協同階段。在適應階段，各備選解利用積累的數據不斷調整自身模態；在協同階段，各備選解之間通過數據交換，最終共同向更優的解逼近。

3.2 改進的蟻群算法

算法為了表示最優路徑和實際行走路徑之間的互信息熵，在蟻群算法的概率算子中增加了一個相似度影響因子：

其中：

i:待測路徑上的節點

j:最優路徑上的節點

Ii，j:為i與j之間的互信息

p(i，j):為i節點和j節點的聯合概率分布

p(i):i節點的邊緣概率分布

p(j):j節點的邊緣概率分布

本方法使用聯合直方圖法對互信息進行計算。

最優路徑的存在會對蟻群的搜索方向起到引導作用，而互信息則為主要的引導元素，蟻群會偏向于選擇與當前狀態互信息最大的節點作為下一個目標。同時，將該影響因子引入蟻群算法，路徑選擇概率函數改寫為：

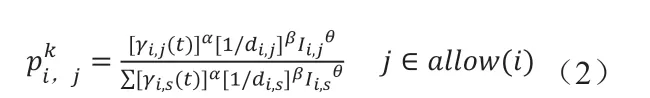
其中：

圖1：測試數據自動生成模型

圖2：直角三角形最優個體迭代次數算法比對

[γi，j(t)]α:在t時刻散布在第i個節點和第j個節點間的互信息

di，j:節點i與節點j之間的距離

allow(i):當蟻群位于第i個節點時未訪問的節點集

α:信息素的關重度

β:可見性的關重度

θ:互信息的關重度

設滿足式（2）的蟻群稱為A類蟻群，該蟻群會因優先選擇互信息量最大的節點導致自身極易易陷入局部最優節點。為了解決陷入局部最優的問題，引入B類蟻群，其γ為A類蟻群的相反數，從而使該蟻群有一定的能力修正局部最優點。

綜上所述，本文改進的蟻群算法步驟如下：

Step1:對參數變量進行初始化；

Step2:使用傳統蟻群算法，蟻群數為m0，迭代次數為n0；

Step3:根據傳統蟻群算法得到的結果，對聯合直方圖矩陣HBT進行初始化；

Step4:把蟻群分為三類，一類為傳統蟻群，另兩類分別為A類蟻群和B類蟻群，蟻群數量分別為m1、m2和m3；

Step5:對三類蟻群的主要參數進行初始化；

Step6:第一類蟻群利用傳統蟻群算法進行計算，之后記錄下其互信息并存儲行進路徑；

Step7:A類和B類蟻群則利用公式（2）進行計算，之后分別記錄下其互信息并存儲行進路徑；

Step8:根據步驟Step6～Step7得到的所有蟻群的路徑集合對聯合直方圖矩陣HBT進行更新；

Step9:判斷計算結果是否收斂或達到最大迭代次數，否則轉到Step5；

Step10:輸出最優路徑即最優解。

4 實驗驗證與分析

本文采用三角形判別問題對算法進行可行性驗證，選取邏輯較復雜且更具代表性的直角三角形判別問題生成測試數據，并把計算結果與傳統蟻群算法進行了對比。

實驗設置三角形的3條邊L1、L2、L3，每個參數占8位，取值范圍為[0，255]，長度為24。例如，三角形L1=6，L2=8，L3=10，則 編 碼 表 示 為（00000110 0000100000001010）。實驗隨機選取15-90個螞蟻數作為初始蟻群，設定三類蟻群數m1=m2=m3，信息素的關重度α為1.5，可見性關重度β為5，互信息關重度θ為2，信息揮發因子為0.5，信息素強度為100，最大迭代次數n0為1000。

實驗開始，輸入被測程序并進行靜態分析，根據分析結果對選定的路徑進行插樁。對直角三角形參數進行初始化，分別執行傳統蟻群算法和改進蟻群算法。調用插裝程序獲得評價值，引導蟻群更新，得到最優測試數據。兩種算法分別運行10次，記錄蟻群規模為15、30、45、60、75、90時的平均迭代次數，見圖2。

實驗結果表明：

（1）在其他參數變量均相同的情況下，隨著蟻群規模的逐步增大，本文改進蟻群算法和傳統蟻群算法生成最優測試數據的平均迭代次數會逐步減小；

（2）在基本參數設置均相同的情況下，對于特定情況的最優測試數據生成，本文改進蟻群算法明顯少于傳統蟻群算法的平均迭代次數；

（3）傳統蟻群算法在運行過程中出現了陷入局部最優的情況，改進蟻群算法有效地彌補了局部最優的缺陷，減小了搜索停滯不前的可能性。

改進的蟻群算法相較傳統蟻群算法，能夠更快速、精確地找到測試數據的可行解。因此，改進的蟻群算法可以使測試數據自動生成過程更加高效。

5 結束語

本文在蟻群算法的基礎上，提出了一種基于改進的蟻群算法的測試數據自動生成方法。該方法是一種性能優異的搜索算法，具有收斂速度快、全局搜索能力強的優點。