基于改進(jìn)蟻獅算法的MMC控制器PI參數(shù)優(yōu)化研究

田錄林，陳倩雯，周 萌，張沛文，王偉博，巨思遠(yuǎn)

（1. 西安理工大學(xué)，陜西 西安 710048； 2. 工商銀行陜西分行反洗錢中心，陜西 西安 715111）

0 引 言

模塊化多電平換流器（Modular Multilevel Converter，MMC）作為電壓源型換流器的一種新型拓?fù)浣Y(jié)構(gòu)，具有實(shí)現(xiàn)功率獨(dú)立可調(diào)、無(wú)需額外的濾波裝置、占地面積小和結(jié)構(gòu)模塊化等優(yōu)點(diǎn)，目前已在國(guó)內(nèi)外實(shí)際工程中投入運(yùn)行[1]。多模塊的拓?fù)浣Y(jié)構(gòu)和多環(huán)節(jié)的控制策略，在仿真研究和工程實(shí)踐中需要考慮復(fù)雜的協(xié)調(diào)控制，因而對(duì)控制系統(tǒng)的性能要求非常高[2]。比例積分（PI）控制因調(diào)節(jié)快速、結(jié)構(gòu)簡(jiǎn)單等優(yōu)點(diǎn)，被廣泛用于 MMC 的控制環(huán)節(jié)設(shè)計(jì)。 PI 控制參數(shù)的選取對(duì)系統(tǒng)性能有重大影響，隨著研究發(fā)展，智能優(yōu)化算法越來(lái)越多地被應(yīng)用于 PI 控制參數(shù)的優(yōu)化，如粒子群算法（Particle Swarm Optimization， PSO）等[3]。蟻獅優(yōu)化算法（AntLion Optimizer， ALO）是 2015 年新提出的仿生算法，通過(guò)模擬螞蟻圍繞蟻獅游走的生物行為，實(shí)現(xiàn)對(duì)解空間的全局搜索，通過(guò)向精英蟻獅學(xué)習(xí)的機(jī)制保證種群的多樣性。經(jīng)工程實(shí)踐驗(yàn)證， ALO 算法具有調(diào)節(jié)參數(shù)少、求解精度高等優(yōu)點(diǎn)。文獻(xiàn) [4] 提出一種基于 Fuch 映射的混沌偵查機(jī)制的改進(jìn) ALO 算法，減少了初始適應(yīng)值較差個(gè)體對(duì)種群的誤導(dǎo)，但并未改善算法的收斂速度。文獻(xiàn) [5] 針對(duì)原始 ALO 算法搜索半徑呈跳躍式，搜索更偏向于精英，易陷入局部最優(yōu)；引入動(dòng)態(tài)搜索和尋優(yōu)半徑連續(xù)收縮機(jī)制改進(jìn) ALO 算法，使改進(jìn) ALO 算法具有了更好的收斂速度，但降低了對(duì)已找到的最優(yōu)解充分利用的能力。文獻(xiàn) [6] 通過(guò)在建模中引入漩渦收斂方式，增強(qiáng)了原算法對(duì)最優(yōu)解的利用能力，但忽略了保持種群進(jìn)化的多樣性，使算法陷入了局部最優(yōu)解。

本文提出一種改進(jìn)蟻獅算法。引入 Tent 映射的混沌思想，利用混沌的遍歷性細(xì)化算法中優(yōu)化變量的搜索空間，保證初始化粒子具有更好的多樣性，克服原蟻獅算法存在的收斂速度慢、易陷入局部最優(yōu)等缺陷。同時(shí)，引入精英競(jìng)爭(zhēng)策略，充分利用已經(jīng)找到的最優(yōu)解，幫助種群快速選定更優(yōu)區(qū)域，大幅減少計(jì)算量，也保證了算法的收斂速度。以反應(yīng)系統(tǒng)調(diào)節(jié)品質(zhì)的時(shí)間乘絕對(duì)誤差積分 ITAE 值作為目標(biāo)函數(shù)，將改進(jìn)算法用于MMC 控制環(huán)節(jié)的 PI 參數(shù)整定，與其他智能算法結(jié)果作對(duì)比，證明改進(jìn)后算法存在優(yōu)越性。此改進(jìn)算法對(duì)選取較優(yōu) PI控制參數(shù)、提高控制系統(tǒng)性能有一定的實(shí)際參考意義。

1 模塊化多電平換流器拓?fù)浼肮ぷ髟?/h2>

三相 MMC 拓?fù)鋱D如圖 1 所示，每相由上、下橋構(gòu)成，共6個(gè)橋臂，每個(gè)橋臂由N個(gè)子模塊和1個(gè)橋臂電感L串聯(lián)而成。橋臂電感L可以抑制直流側(cè)故障時(shí)產(chǎn)生的短路電流和橋臂間的交流環(huán)流[7]。

圖1 MMC拓?fù)鋱D

當(dāng)T1加開(kāi)通信號(hào)，T2加關(guān)斷信號(hào)，MMC為投入狀態(tài)；當(dāng)T1加關(guān)斷信號(hào)，T2加開(kāi)通信號(hào)，MMC為旁路狀態(tài)；當(dāng)T1和T2都加關(guān)斷信號(hào)，此時(shí)處于閉鎖狀態(tài)。MMC正常工作需要每相投入n個(gè)子模塊，通過(guò)調(diào)整n個(gè)子模塊在上下橋臂的分布實(shí)現(xiàn)不同電平的輸出[8]。圖2為MMC簡(jiǎn)化等效電路。

基于圖2的MMC等效電路，可得到MMC交流三相電路在abc坐標(biāo)系下的數(shù)學(xué)模型：

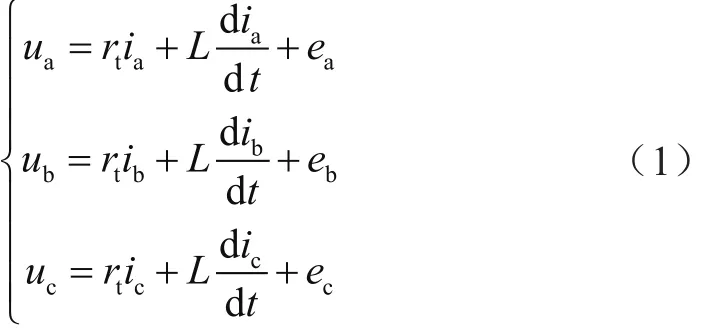
其中，L=lt+ls/2，ea、eb、ec為MMC的三相輸出電壓。

對(duì)式（1）進(jìn)行dq軸坐標(biāo)變換，得到dq軸下的MMC數(shù)學(xué)模型為：

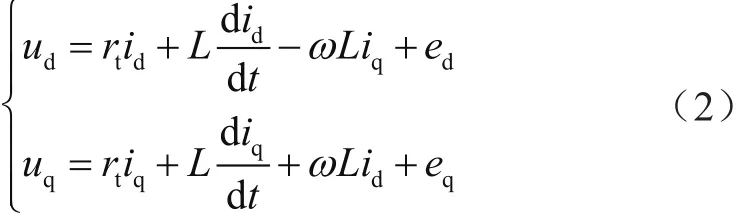
其中，ud、uq為接入點(diǎn)電壓在dq軸坐標(biāo)系下的d軸和q軸分量；ed、eq為MMC可控輸出電壓的d軸和q軸分量；id、iq為經(jīng)過(guò)換流變壓器流入MMC的電流dq軸分量；ω為交流系統(tǒng)角頻率。由式（2）可知，dq軸電壓方程存在電流耦合，ωLiq、ωLid為交叉耦合項(xiàng)[9]。

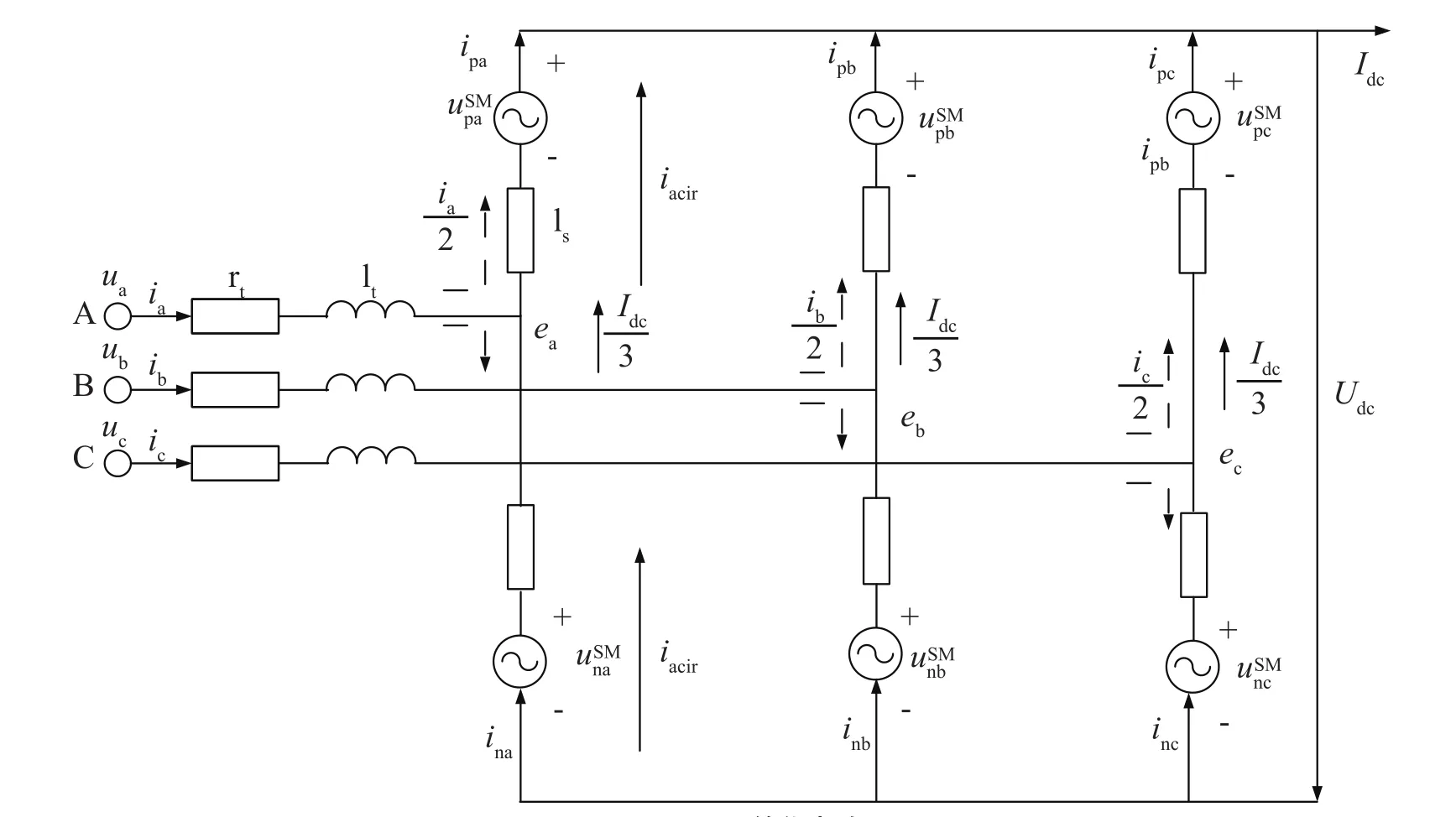
圖2 MMC簡(jiǎn)化電路

2 MMC控制策略

MMC控制系統(tǒng)常采用直接電流控制，控制器為雙閉環(huán)控制方式，即外環(huán)控制和內(nèi)環(huán)控制，其控制框圖如圖3所示。

本文使用的外環(huán)控制方式為定直流電壓、無(wú)功功率控制，內(nèi)環(huán)采用電流控制。外環(huán)控制根據(jù)無(wú)功功率和直流電壓的參考值，計(jì)算內(nèi)環(huán)dq軸電流參考值；內(nèi)環(huán)控制使dq軸電流快速跟蹤其參考值。

2.1 內(nèi)環(huán)控制

引入虛擬控制量，即：

圖3 MMC雙閉環(huán)控制框圖

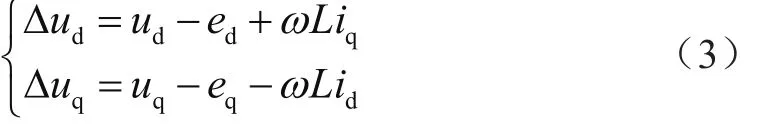
依式（2）可知：

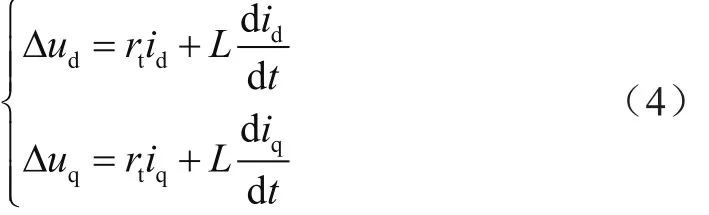
將電流偏差值作為控制器的輸入，Δud和Δuq作為控制器的輸出，則可得：

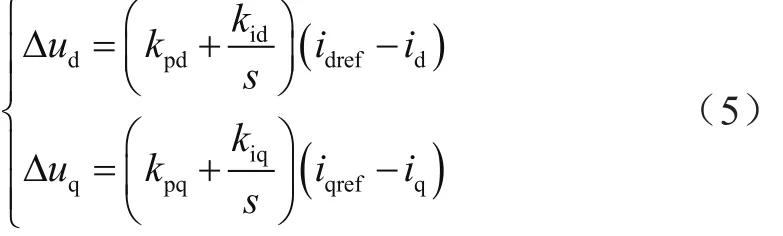
其中，idref、iqref分別為dq軸電流的參考值，通過(guò)引入虛擬控制量實(shí)現(xiàn)id、iq的解耦，減少dq軸之間的影響。

2.2 外環(huán)控制

外環(huán)控制環(huán)節(jié)通過(guò)對(duì)直流電壓、無(wú)功功率指令控制，生成內(nèi)環(huán)需要的參考電流值idref和iqref：

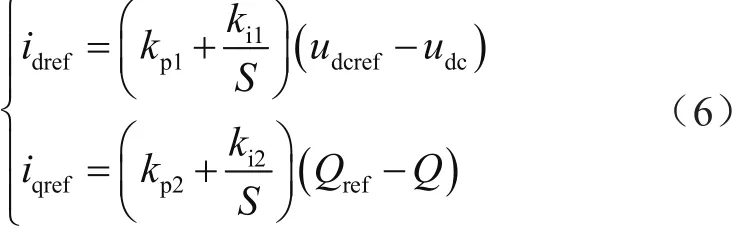
其中，udcref為MMC直流電壓udc的參考值；Qref為交流側(cè)輸入的無(wú)功功率Q的參考值。

當(dāng)外環(huán)為直流電壓控制回路運(yùn)行時(shí)，若直流電壓低于其參考值，PI控制器增大d軸電流分量參考值，通過(guò)對(duì)電容充電升高直流電壓；若直流電壓高于其參考值，PI控制器減小d軸電流分量參考值，對(duì)電容放電降低直流電壓。在換流器容量范圍內(nèi)，通過(guò)調(diào)節(jié)能量平衡，直流電壓被控制在參考值附近。最后，將計(jì)算的d軸和q軸電流參考值發(fā)給內(nèi)環(huán)控制器。

3 蟻獅算法及其改進(jìn)算法

3.1 原始蟻獅算法

蟻獅算法源自于模擬蟻獅捕獵螞蟻的行為。蟻獅即問(wèn)題的解，捕獲適應(yīng)度更高的螞蟻即更新并保存更優(yōu)解[10]。

3.1.1 螞蟻隨機(jī)游走

螞蟻隨機(jī)游走過(guò)程即視作各搜索代理搜尋可行域的過(guò)程：

其中，X(t)是螞蟻隨機(jī)游走步數(shù)集，cumsum是螞蟻游走位置累積和，t為游走步數(shù)，tmax是隨機(jī)最大游走步數(shù)（最大迭代次數(shù)）。r(t)為自定義隨機(jī)函數(shù)，rand是[0，1]上均勻分布的隨機(jī)數(shù)。

為了保證螞蟻隨機(jī)游走在可行域的范圍內(nèi)不越界，需要進(jìn)行歸一化處理：

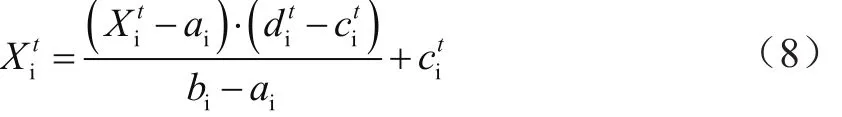
其中，ai和bi為第i個(gè)變量隨機(jī)游走的最小值和最大值；和為第i個(gè)變量在第t代的最小值和最大值。

3.1.2 螞蟻爬入陷阱

蟻獅的位置影響螞蟻游走的區(qū)域邊界范圍：

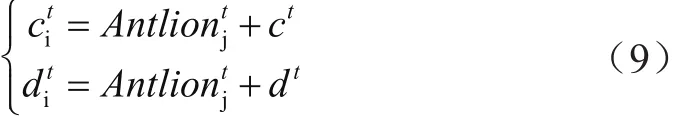
其中，Antlionjt為第j只螞蟻選擇的相應(yīng)的蟻獅在第t代的位置；dt為所有變量在第t代的最大值；ct為所有變量在第t代的最小值。

3.1.3 蟻獅捕食

當(dāng)螞蟻落入陷阱蟻獅會(huì)揚(yáng)沙，可通過(guò)急劇減小螞蟻的游走范圍來(lái)阻止螞蟻逃脫，即隨著迭代次數(shù)的增加，上界和下界減小。

其中，I=10ωt/T，ω是一個(gè)由t和T定義的隨迭代次數(shù)增大的常數(shù)，t為當(dāng)前迭代次數(shù)，T為最大迭代次數(shù)，當(dāng)t＜0.1T時(shí)，I=1。

而當(dāng)有螞蟻適應(yīng)度大于蟻獅的適應(yīng)度值時(shí)，認(rèn)為該螞蟻被蟻獅捕獲，需根據(jù)螞蟻位置更新蟻獅位置：

3.1.4 精英策略

精英蟻獅是每代適應(yīng)度最高的蟻獅。第t次迭代的第i只螞蟻在第t+1次迭代時(shí)的位置為：

3.2 改進(jìn)后的蟻獅算法

ALO算法前期，種群中存在適應(yīng)度值較差的個(gè)體，即離最優(yōu)解較遠(yuǎn)的解。若螞蟻圍繞這些適應(yīng)度值較差的蟻獅游走，則易陷入局部最優(yōu)，減弱算法的尋優(yōu)效果，影響算法的收斂速度。此時(shí)，鑒于混沌具有遍歷性，可利用混沌序列初始化種群位置，以保證初始化的隨機(jī)性。

3.2.1 基于改進(jìn)Tent映射的混沌初始化

本文采用改進(jìn)Tent映射[10-13]種群位置進(jìn)行初始化。Tent映射表達(dá)式為：

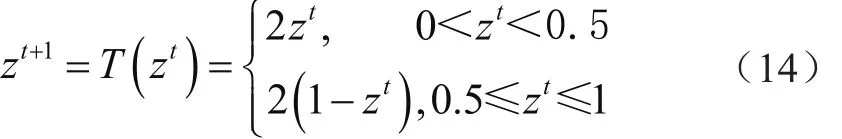
其中，zt代表代表混沌變量第t次迭代計(jì)算得到的值；zt取值范圍在（0，1]。

對(duì)式（14）中變量zt分別賦予n個(gè)（0，1）上隨機(jī)不等的初始值。由于Tent映射迭代序列中存在小周期和不穩(wěn)定周期點(diǎn)，如0.25、0.5、0.75都將迭代到不動(dòng)點(diǎn)，因此將Tent映射加以改進(jìn)，即當(dāng)zt=0.25、0.5、0.75或zt=zt-m(m=1,2,3,4)時(shí)，公式采用：

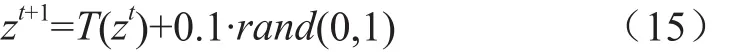
利用隨機(jī)函數(shù)對(duì)序列進(jìn)行擾動(dòng)，跳出小周期點(diǎn)或不動(dòng)點(diǎn)，使重新進(jìn)入混沌狀態(tài)。

上述改進(jìn)后，Tent映射可得到n個(gè)運(yùn)動(dòng)軌跡完全不同的混沌變量為當(dāng)前最優(yōu)解。然后，將混沌變量的取值范圍轉(zhuǎn)換到相應(yīng)優(yōu)化變量的取值范圍[14]，即可得到混沌初始化后的種群初始值：

其中，aj、bj均為常數(shù)，是優(yōu)化變量約束的上、下限。

3.2.2 精英競(jìng)爭(zhēng)策略

由于上一代精英蟻獅影響下一代螞蟻的行動(dòng)，而單個(gè)精英所擁有的極值信息非常有限，因此以個(gè)別精英蟻獅為中心的區(qū)域搜索會(huì)導(dǎo)致算法出現(xiàn)早熟現(xiàn)象。因此，本文采取建立精英庫(kù)，存儲(chǔ)歷代適應(yīng)度值較佳的個(gè)體，每次迭代時(shí)從精英庫(kù)中選取精英進(jìn)行競(jìng)爭(zhēng)，而不使用輪盤賭進(jìn)行選擇，有利于加快算法的收斂速度。設(shè)置精英個(gè)數(shù)[nmin,nmax]，第t代精英個(gè)數(shù)為n(t)。迭代前期應(yīng)盡可能多選擇精英參與競(jìng)爭(zhēng)，后期為減少計(jì)算量、提高計(jì)算速度與效率，應(yīng)減少選擇的精英數(shù)量。因此，精英個(gè)數(shù)應(yīng)隨著迭代次數(shù)逐次減少[14-16]，計(jì)算公式為：

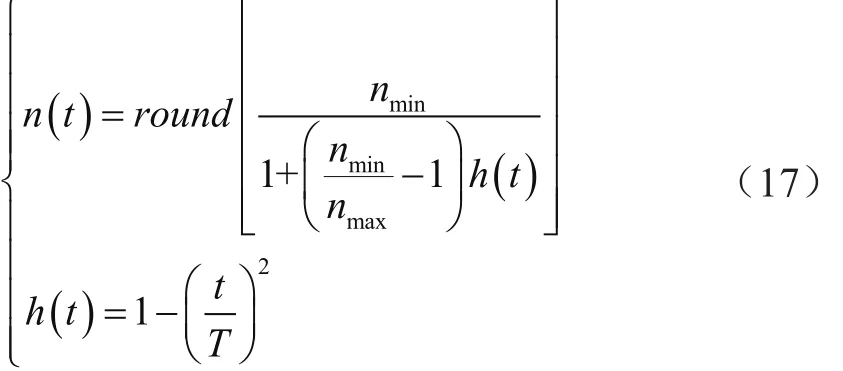
其中，round為取整函數(shù)，T為最大迭代次數(shù)。

每次迭代尋優(yōu)完成后，更新精英庫(kù)的精英，保證每次迭代中的最優(yōu)n個(gè)個(gè)體，即每次迭代初始化后，先由式（17）確定精英蟻獅個(gè)數(shù)，再讓螞蟻圍繞蟻獅進(jìn)行游走，但游走邊界公式改為：

其中，是精英庫(kù)里選取的精英蟻獅。

于是，式（12）改為：

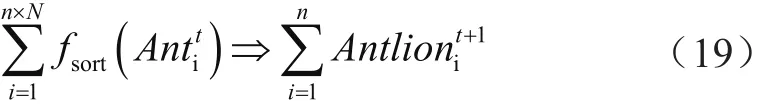
其中，是排序函數(shù)，表示提取排序后的前n個(gè)較優(yōu)個(gè)體。

4 PI參數(shù)優(yōu)化

由圖3可知，MMC雙閉環(huán)控制中共使用了4個(gè)PI控制器。為簡(jiǎn)化控制環(huán)節(jié)，假設(shè)內(nèi)環(huán)2個(gè)控制器PI參數(shù)相同，取X=[kp1,ki1,kp2,ki2,kp,ki]為優(yōu)化目標(biāo)，時(shí)間乘絕對(duì)誤差積分ITAE[17]作為目標(biāo)函數(shù)：

其中，e(t)為相應(yīng)控制目標(biāo)參考值與實(shí)際值的誤差；T為時(shí)間定值，一般取較大值讓系統(tǒng)進(jìn)入穩(wěn)定。優(yōu)化的目的是讓優(yōu)化目標(biāo)的實(shí)際值更好地跟蹤參考值，即希望誤差e(t)最小，即求取JITAE最小值。ITAE值能反應(yīng)系統(tǒng)調(diào)節(jié)品質(zhì)，值越小，系統(tǒng)響應(yīng)速度越快。

算法優(yōu)化步驟：

（1）采用改進(jìn)Tent映射混沌初始化螞蟻和蟻獅種群；

（2）計(jì)算所有螞蟻和蟻獅的適應(yīng)度值，按適應(yīng)度降序排列，選擇適應(yīng)度最大的蟻獅為精英蟻獅；

（3）建立精英蟻獅庫(kù)，設(shè)置精英庫(kù)中蟻獅個(gè)數(shù)，在精英庫(kù)中選擇蟻獅，讓螞蟻圍繞精英蟻獅進(jìn)行游走；

（4）標(biāo)準(zhǔn)化螞蟻游走范圍；

（5）利用式（18）更新螞蟻的位置；

（6）計(jì)算所有螞蟻的適應(yīng)度值，將螞蟻和上一代蟻獅組合，并按適應(yīng)值降序排列；

（7）選擇當(dāng)代蟻獅種群適應(yīng)度值最大的為精英蟻獅，回到步驟（1）循環(huán)至迭代次數(shù)最大。

5 仿真驗(yàn)證

5.1 典型目標(biāo)函數(shù)性能測(cè)試

單峰值函數(shù)Rosenbrock：

多峰值函數(shù)Rastrigin：

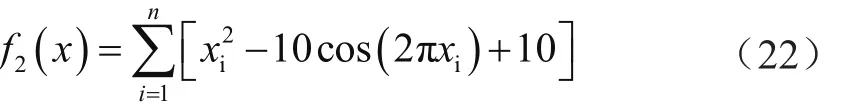
使用式（21）和式（22）兩個(gè)典型目標(biāo)函數(shù)，對(duì)改進(jìn)后ALO算法進(jìn)行性能測(cè)試，并與原始ALO算法和PSO算法進(jìn)行數(shù)據(jù)對(duì)比。測(cè)試條件：群體規(guī)模20，最大迭代次數(shù)50，維數(shù)為8。于是，改進(jìn)ALO算法、原始ALO算法及PSO算法對(duì)目標(biāo)函數(shù)的仿真結(jié)果數(shù)據(jù)，如表1所示。

表1 3種算法典型函數(shù)測(cè)試結(jié)果

仿真得到由改進(jìn)ALO算法優(yōu)化的兩種測(cè)試函數(shù)最優(yōu)適應(yīng)度值曲線圖，橫坐標(biāo)為迭代次數(shù)，縱坐標(biāo)為最優(yōu)適應(yīng)度值，如圖4、圖5所示。

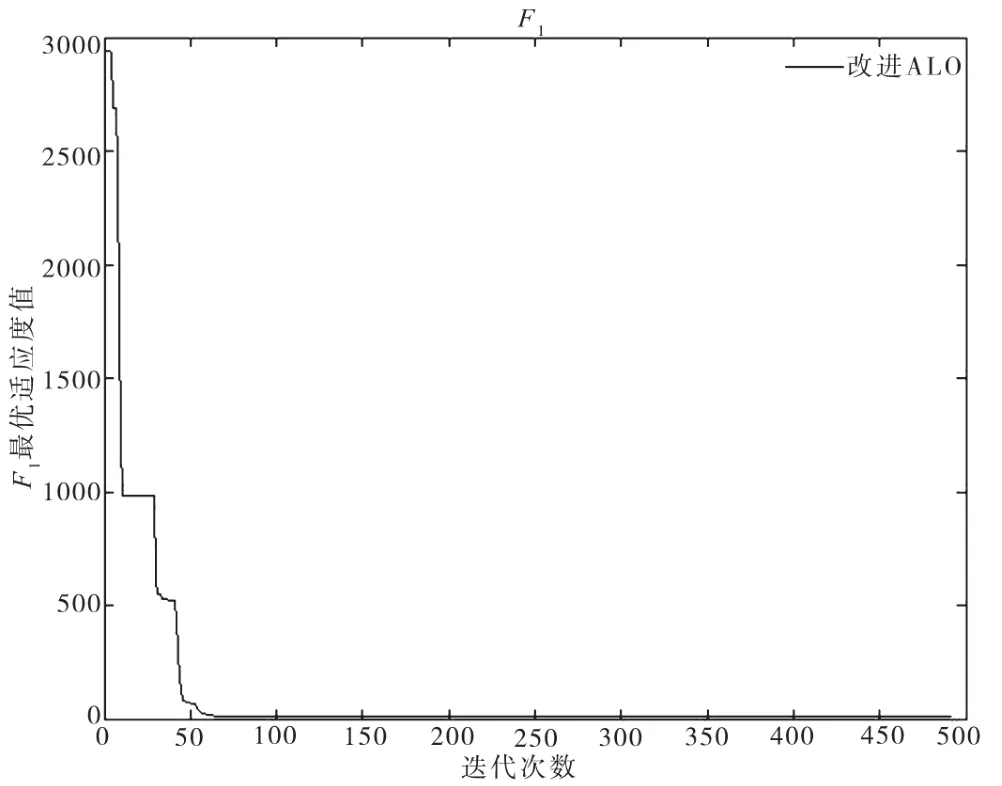
圖4 F1最優(yōu)適應(yīng)度值曲線

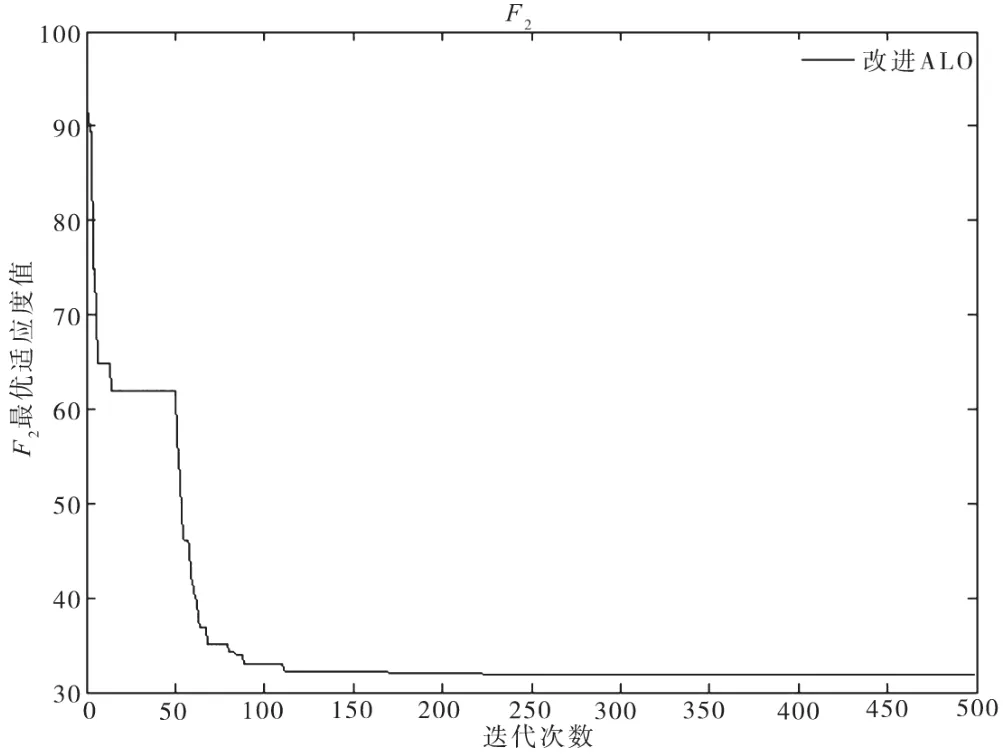
圖5 F2最優(yōu)適應(yīng)度值曲線

5.2 MMC PI控制參數(shù)優(yōu)化仿真

本文在PSCAD中搭建雙端21電平MMC-HVDC系統(tǒng)，其拓?fù)浣Y(jié)構(gòu)如圖6所示。采用MATLAB與PSCAD之間的數(shù)據(jù)相互調(diào)用進(jìn)行參數(shù)優(yōu)化過(guò)程的適應(yīng)值計(jì)算和優(yōu)化結(jié)果的仿真驗(yàn)證，仿真參數(shù)見(jiàn)表2。

表2 MMC-HVDC仿真參數(shù)

系統(tǒng)采用最近電平逼近調(diào)制策略，送端采用定直流電壓和定無(wú)功功率控制。系統(tǒng)頻率50 Hz，直流線路極間電壓500 kV，輸送功率400 MW，換流采用CCSC抑制方式。蟻獅種群數(shù)為20，迭代次數(shù)為20次，維數(shù)為8。

采用粒子群算法、傳統(tǒng)蟻獅算法和改進(jìn)后的蟻獅算法的仿真計(jì)算結(jié)果見(jiàn)圖7。

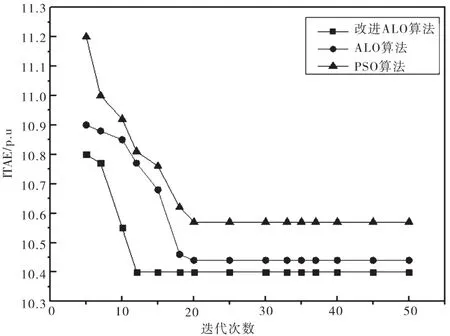
圖7 ITAE指標(biāo)對(duì)比圖

由圖7可知，PSO和ALO算法都經(jīng)過(guò)約18次迭代曲線趨于收斂，而改進(jìn)ALO只需要經(jīng)過(guò)12次迭代曲線就開(kāi)始收斂，證明改進(jìn)算法收斂性能優(yōu)于傳統(tǒng)算法。同時(shí)，改進(jìn)蟻獅算法優(yōu)化得到的最終ITAE值小于傳統(tǒng)蟻獅算法優(yōu)化得到的ITAE值，優(yōu)化效果更突出。

圖6 MMC-HVDC系統(tǒng)仿真模型

此外，加入標(biāo)準(zhǔn)遺傳算法、標(biāo)準(zhǔn)蟻群算法與改進(jìn)ALO算法的橫向比較，以驗(yàn)證改進(jìn)算法的優(yōu)越性，結(jié)果見(jiàn)圖8。

由圖8可知，標(biāo)準(zhǔn)蟻群算法和標(biāo)準(zhǔn)遺傳算法的收斂速度比之改進(jìn)ALO算法慢，最終ITAE值也偏大，優(yōu)化效果改進(jìn)ALO算法最佳。

通過(guò)幾種算法對(duì)比可證明，本文改進(jìn)算法具有一定的優(yōu)越性。用上述5種算法分別進(jìn)行10次優(yōu)化，由于數(shù)據(jù)繁多，表3僅列出了10次優(yōu)化中得到最小ITAE值時(shí)的最優(yōu)PI參數(shù)。

通過(guò)表3數(shù)據(jù)對(duì)比可發(fā)現(xiàn)，改進(jìn)ALO算法得到的值最小。未列出數(shù)據(jù)表明，每次優(yōu)化改進(jìn)ALO算法得到的值都小于其余幾種算法，證明本文改進(jìn)算法具有優(yōu)勢(shì)。ITAE值的減小，說(shuō)明系統(tǒng)動(dòng)態(tài)響應(yīng)速度得到了提高，且通過(guò)本文改進(jìn)算法提高的效果最好。將優(yōu)化前后的參數(shù)代入模型進(jìn)行仿真，可以得到如圖9～圖12所示的波形。比較圖9、圖10，參數(shù)優(yōu)化后，A相橋臂內(nèi)部環(huán)流大小由原來(lái)的[-1.5，1.5] A減小為[-0.6，0.6]A，說(shuō)明優(yōu)化后參數(shù)增強(qiáng)了系統(tǒng)的環(huán)流抑制能力。同時(shí)，由于橋臂環(huán)流得到了抑制，上橋臂的電流波形畸變也減小了。

表3 5種算法優(yōu)化后最優(yōu)結(jié)果對(duì)比

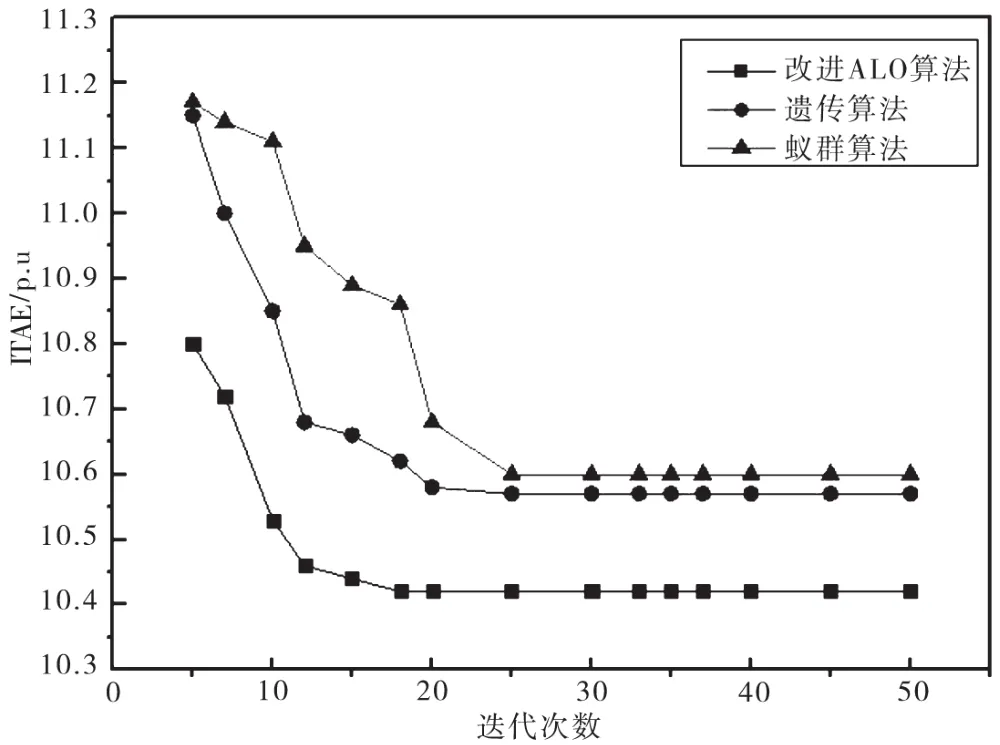
圖8 ITAE指標(biāo)圖

6 結(jié) 論

針對(duì)模塊化多電平換流器控制系統(tǒng)多個(gè)PI控制器PI參數(shù)優(yōu)化困難的問(wèn)題，在現(xiàn)有MMC最近電平逼近調(diào)制策略基礎(chǔ)上，提出基于改進(jìn)蟻獅算法的控制器PI參數(shù)優(yōu)化方法。改進(jìn)方面主要集中解決原算法易陷入局部最優(yōu)及收斂速度慢等問(wèn)題。具體地，引入Tent映射的混沌思想，在初始化種群時(shí)增加變量取值多樣性，避免算法陷入局部最優(yōu)；融合精英競(jìng)爭(zhēng)，加快算法收斂速度，減少計(jì)算量；取系統(tǒng)指標(biāo)ITAE值作為目標(biāo)函數(shù)，用以衡量參數(shù)優(yōu)化效果。通過(guò)MATLAB與PSCAD之間的聯(lián)合調(diào)用及數(shù)據(jù)交互，對(duì)MMC雙閉環(huán)控制環(huán)節(jié)的控制器PI參數(shù)進(jìn)行優(yōu)化，并對(duì)比多個(gè)算法的優(yōu)化效果。仿真結(jié)果表明：改進(jìn)后的算法尋優(yōu)精度更好，收斂速度更快，且使用改進(jìn)算法優(yōu)化的控制器PI參數(shù)可以有效改善電流波形，提高系統(tǒng)動(dòng)態(tài)性。

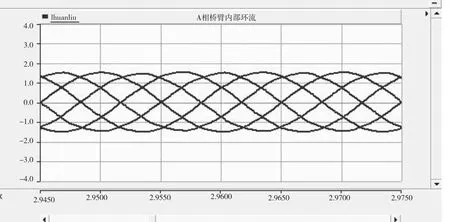
圖9 優(yōu)化前A相環(huán)流波形

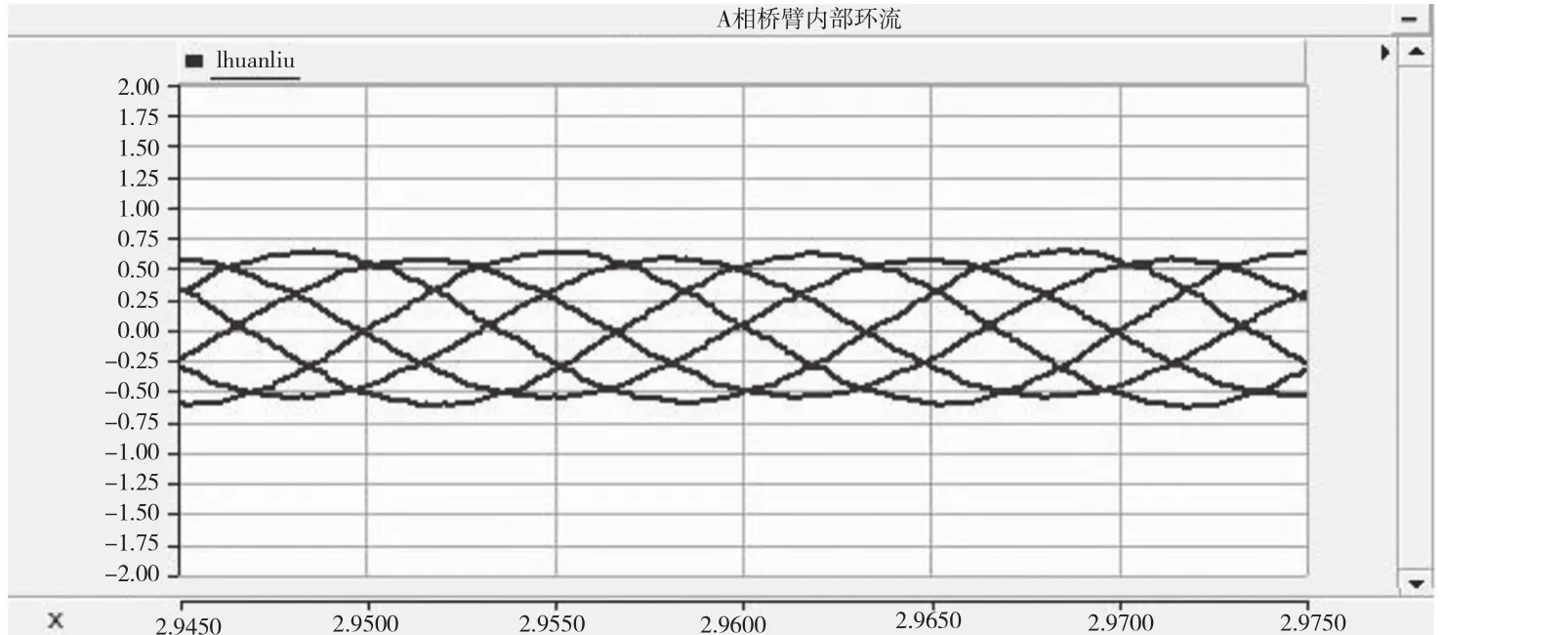
圖10 優(yōu)化后A相環(huán)流波形

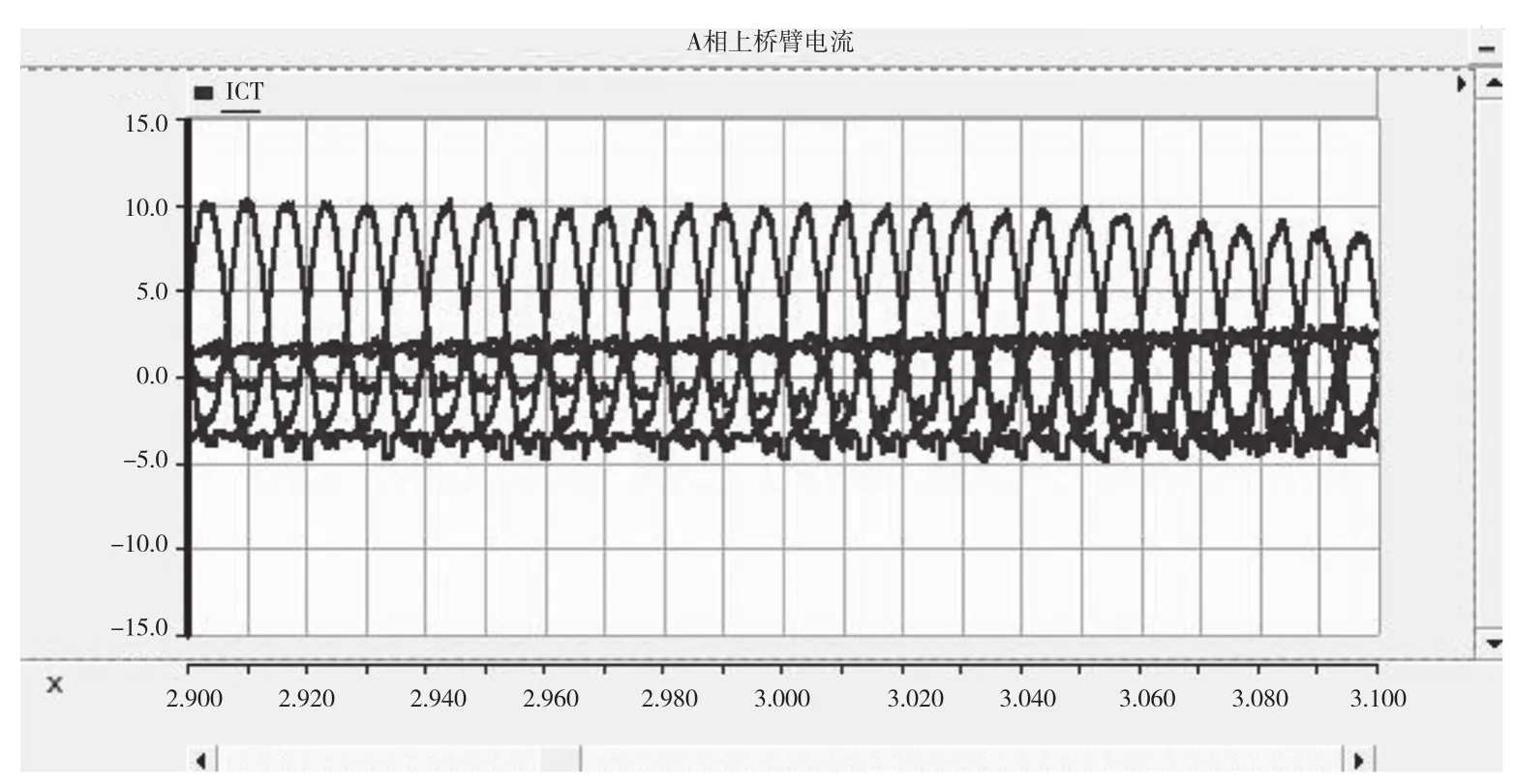
圖11 優(yōu)化前A相上橋臂電流

圖12 優(yōu)化后A相上橋臂電流